线性规划问题的三个方面

◎王军红

(西安市远东第一中学，陕西　西安　710000)

线性规划知识自进入中学数学教材以来，就受到了高考命题专家、数学研究者和广大的中学数学教师的青睐.线性规划习题取材广泛、形式灵活、背景新颖，恰当地融数的分析于形的直观推理之中，成为命制高考试题的新阵地.要充分学好线性规划内容，作为一名高中数学教师，我通过近几年的教学实践，特别是新课改下的教学实践，觉得要掌握好线性规划知识及其应用、提升解题能力，需要从以下几个方面努力.

一、注重程序，实现解题模式的格式化

在中学数学教学中“注重通性通法，淡化特殊技巧”是高考早已提出的要求.线性规划问题的基本解题思路是“画图→平移求点→代值解答”.其中，规范作图是准确解答的基础.不仅要规范地作出可行域，还要能准确体现出线性目标函数与可行域边界在倾斜程度上的差异.举例如下.

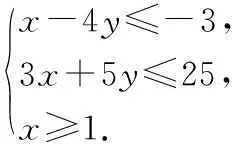
图1

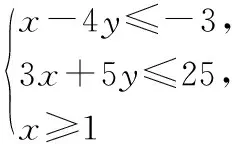
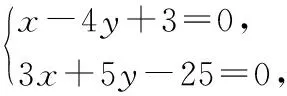
点评用线性规划求最值是数形结合的一个重要方面，它使众多变量汇聚的代数问题变得直观、简捷，而规范的作图则是成功求解的基础.线性规划的这一基本应用程序要让学生形成熟练的解题模式.

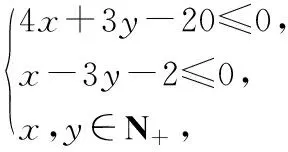
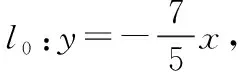
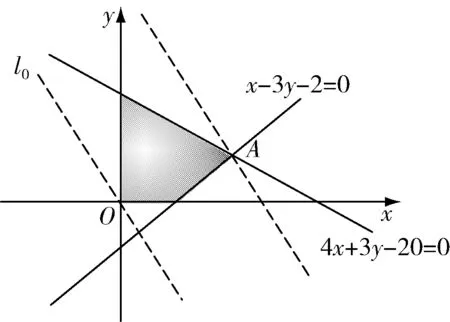
图2

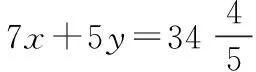
点评处理线性规划整数解问题的基本思路是：若顶点恰为整数，则它就是最优解；若不是整数点，应先求出该点坐标，并计算目标函数z的值，而后在可行域内适当放缩目标函数的值，使其为整数且距离z最近，依次找点求最值.

读者不妨练习：某实验室需购买某种化工原料106 kg.现在市场上该原料有两种包装，一种是每袋35 kg，价格是140元；一种是每袋24 kg，价格是120元.在满足需要的前提下，最少要花费多少元？

二、挖掘潜力，提升应用能力

可行域是线性规划问题研究的重点，确定可行域的基本方法是：直线定界，特点定域.确定区域时遵循：同侧同号，异侧异号.

例3已知直线l过点P(-1，2)且与以A(-2，-3)，B(3，0)为端点的线段有公共点，求直线l的斜率k的取值范围.

图3

解析(当然此题有多种不同的解法，这里仅用可行域的思想求解)设直线l的方程为y-2=k(x+1)，令f(x，y)=kx-y+k+2，A，B不落在l的同侧，又l可过A，B两点，所以f(-2，-3)·f(3，0)≤0，

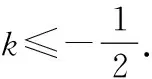
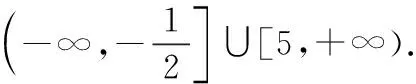
点评当然本题的解答有多种方法，而且此法并非最简.但从利用可行域的思想可以看出，上述解法新颖独特，别具一格，而且很好地回避了k的正负分类讨论.

类似地练习：若直线l1：y=kx+2与l2：y=-2x+4的交点在第一象限内，求k的取值范围.

三、发散思维，拓展应用层次

线性目标函数具有明显的几何意义，学习时要充分挖掘目标函数的几何意义，常见的目标函数有以下几种类型：

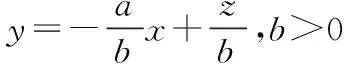
(2)距离型z=(x-a)2+(y-b)2，即z的几何意义为可行域内的动点(x，y)与定点(a，b)的距离的平方；

解析设f(x)=x2+ax+2b，由方程x2+ax+2b=0的一个根在(0，1)内，另一根在(1，2)内可知

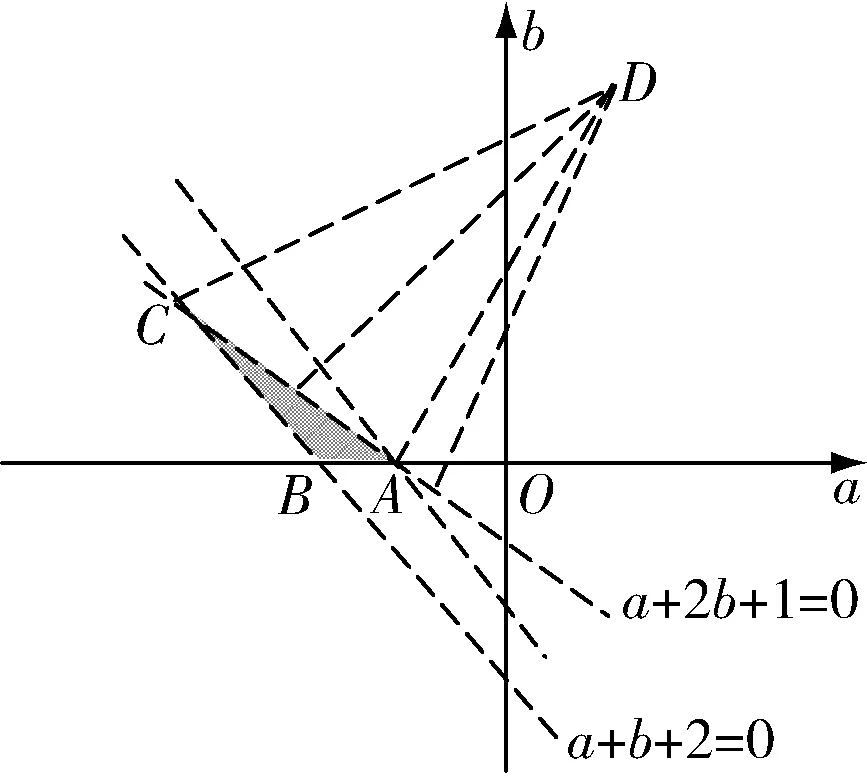
图4

设P(a，b)为上述不等式组所确定的可行域(如图4所示阴影部分)内的任一动点，A(-1，0)，B(-2，0),C(3，0).

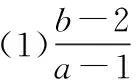
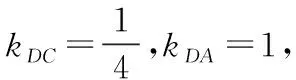
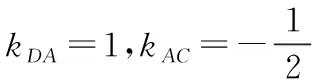
又BD2=13，而DA2=8，DC2=17，

∴(a-1)2+(b-2)2的取值范围是(8，17).

(3)令z=a+b-3，结合图形可知，当l：a+b-3=0平移分别过点A，B时，z值分别取最大值、最小值，依次为-4，-5，∴z=a+b-3的取值范围为(-5，-4).

实践表明，充分重视以上三个方面的学习与练习，能促进学生对线性规划的理解以及应用能力的提升.