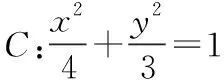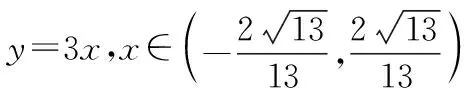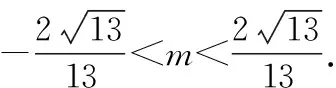圆锥曲线中一题多解一例

◎王　坚

(昆明市第十二中学，云南　昆明　650041)

该题是一个集直线与圆锥曲线位置关系、点与圆锥曲线的位置关系、中点弦、方程与不等式等数学知识于一体的典型案例.《数学考试说明》告诉我们：在知识网络交汇处、思想方法的交汇线和能力层次的交叉区设置问题.

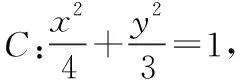
法一点差法(涉及中点问题，是应该想到的常规方法，重点讲解).

解设椭圆上关于l对称的两点分别为A(x1，y1)，B(x2，y2)，弦AB的中点为M(x0，y0)，代入椭圆方程后作差，得

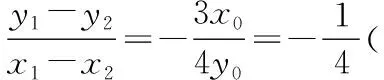
①

由点M(x0，y0)在直线l：y=4x+m上，得y0=4x0+m(点在直线上).

②

由①②解得x0=-m，y0=-3m.

因为点M(x0，y0)在椭圆的内部，

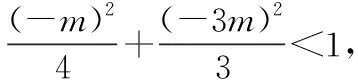
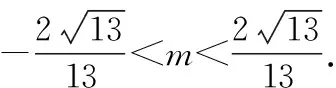
分析两点A，B关于直线l对称(对称的特征：垂直与平分——斜率和中点).

法二韦达定理法(涉及直线与圆锥曲线问题时，一般会想到的方法，重点讲解).

解椭圆上存在两点A，B关于直线l：y=4x+m对称.

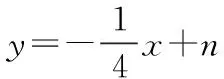
则直线AB与椭圆有两个不同的交点，

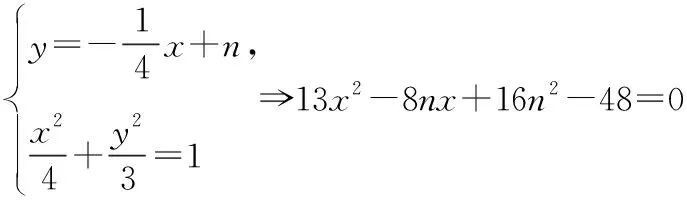
Δ=-192(4b2-13)>0(存在，小心会漏掉)，

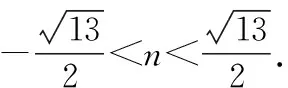
①

(仅有这两点还不够，因为最容易出漏洞的是：保证存在.)

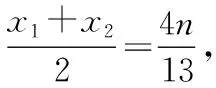
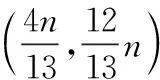
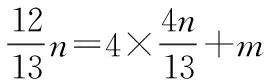
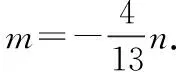
法三平行弦中点轨迹法(类似于点差法，这种方法很特殊，很难想到，可以讲解，不做重点要求).

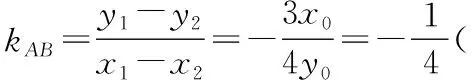
又y0=3x0，