四大策略培养小学生几何直观能力

◎周小青

(厦门市康乐小学，福建　厦门　361000)

《课程标准(2011年版)》中明确指出：几何直观主要是指利用图形描述和分析问题，借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路.几何直观能力主要包括空间想象能力、直观洞察能力和用“图形语言”来思考问题的能力.

一、数形结合，培养学生用图形解决问题的习惯与能力

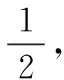
数形结合是第一种重要的数学思想，也是一种重要的数学解题助力器，能使复杂的问题变得直观、简单，从而较好地解决问题.

二、图形动起来，培养学生的空间想象能力

在教学中发现，对于长方体、正方体展开图，学生想象哪个面对应的是哪个面时，有些学生感觉难度较大.教师可引导学生先确定把哪个面设为前面，进行推理想象，然后再借助课件的动态演示，让学生清晰地看到这个展开图是如何形成一个正方体的.在多次的演示中，让学生画出哪些展开图是可以形成一个正方体的.

学习“长方体的认识”一课，教师由一个点，让学生想象，如果让这个点进行运动，想一想你觉得可能形成什么？随着课件的演示，变成了一条线.教师再让学生想象，如果让这条线平移，会变成什么？课件继续验证学生的想象——线变成了面.接下来，如果长方形再沿着一个方向平移，可能变成什么？长方体.教师继续让课件动起来，变成了一个长方体.学生随着课件的直观动态演示，清楚地感受到点—线—面—体之间的关系.有了对点、线、面、体本质的理解，让学生在长方体中找点、线、面，进一步探索长方体就变得简单了.能够体会“点动成线”“线动成面”“面动成体”的现象，空间想象能力也得到了很好的培养.

三、学会表征，提高学生的图形语言能力

表征是客观事物的反映，又是被加工的客体.如何表征是关系到解决问题的重要因素.对于要解决的问题，教师要帮助学生学会选择合适的方法进行表征，以提高学生的图形语言能力.比如，学习“搭配”一课，有三件不同的上衣和两条不同的裙子，一共有多少种不同的穿法？放手让学生用自己喜欢的方式来表达.学生有的用文字，有的用画图，有的用几何图形、有的用字母来代替上衣和裤子，利用连线得出六种不同的穿法.教师让学生观察这几种方法，选择最喜欢的方法，解释为什么.在比较中，学生选择最简单的用字母来代替.有了这样的表征，能简明清楚地表达题意.许多高年级的解决问题，需要借助图形表征来帮助理解，常用的画图包括画线段图、树形图、集合图、示意图等.

四、图形变化，提高直观洞察力

利用图形进行思考，让图形帮助发现、寻找解决问题的思路.在这些图形中，要充分引导学生进行观察、比较，从图形的分析中帮助找到问题的本质.比如，二年级“有余数的除法”一课中，教师通过学生摆正方形，给出8～12根小棒摆出的正方形，借助所画的图形及剩下的根数，让学生观察这些图形及剩下的根数，发现了什么？学生通过对比观察，发现余数都是1，2，3，为什么没有4甚至比4大的数呢？学生发现每个正方形需要有4根，只要有4根就能组成一个正方形，这样的观察分析，学生能直观洞察到与组成的正方形四边有关系.然后紧接着问：如果排成一个五边形，余数可能是几？最小和最大的又是多少？有了正方形直观图作为参照物，提高了学生的直观洞察力，并迁移到五边形、六边形，甚至抽象到具体的除数是几，相应的余数的区间数.

数学发展的历程表明，越是高度抽象的数学内容，往往越需要形象直观的模型作为其解释和支撑，即使是推理几何的功臣欧几里得，在进行几何学的论述过程中仍然依赖了头脑中的图形的直观.正如笛卡儿所确认的：“起始原理本身则仅仅通过直观而得知.”[1]正所谓“物极必反”——越是抽象的数学对象，其数学本质越有可能用简捷而直观的图形来表达.

总之，几何直观是影响中小学生数学发展的重要因素之一，教师要认识到培养学生几何直观的重要性，将几何直观的培养自始至终落实在数学教学的每个环节中.这种教学以保护学生先天的几何直观的潜质作为起点，以有效提升学生的几何直观水平作为终点，最终形成针对几何的敏锐洞察力和深厚的数学素养.