非均质油藏聚合物驱注入参数优化方法与应用
2018-07-14张贤松谢晓庆康晓东陈冠中林春阳
张贤松,谢晓庆,康晓东,陈冠中,林春阳
1)海洋石油高效开发国家重点实验室,北京 100028;2)中海油研究总院有限责任公司技术研发中心,北京 100028
传统上,聚合物驱注入参数的优化设计是对不同注入参数取不同区间值,设计一系列组合方案,通过专用数值模拟软件对所有组合方案进行计算筛选,计算工作量大、耗时长.在低油价形势下,亟待解决非均质油藏聚合物驱注入参数优化,提高其技术经济性[1-6].对于非均质油藏,聚合物驱是分段塞注入的,可通过最优控制和油藏数值模拟确定每个段塞的最优注入浓度和段塞尺寸,这是典型的最优化问题[7-8].梯度类算法在油藏生产优化中应用较广泛,采用有限差分随机逼近方法(finite difference of stochastic approximation, FDSA)梯度近似程度高,收敛速度快,但当控制变量维数较高时,计算量非常大[9].随机扰动逼近算法(simultaneous perturbation stochastic approximation, SPSA)通过对所有的控制变量同时扰动获得近似梯度,计算量不随控制变量个数的增加而增加,但SPSA算法对不同控制变量的扰动量所引起的优化指标函数改变量相差较大,计算得到的SPSA梯度近似精度低,收敛速度慢[10-13].针对上述两种优化方法,本研究提出随机扰动逼近改进新算法(simultaneous perturbation stochastic approximation algorithm, SPSA-FDG),是由FDSA引导的SPSA,在迭代过程中,根据性能指标函数对各控制变量的敏感性变化,实时调整各控制变量扰动步长的大小,以使各控制变量所引起的性能指标函数改变量近似相等,保证计算得到的各控制变量SPSA近似梯度大小比例与FDSA算法类似,从而提高收敛速度.应用研究表明,SPSA-FDG新算法具有迭代计算次数少、梯度估计精度高和收敛性好等优势,高效解决了非均质油藏分段塞聚合物驱注采参数优化求解难题.在聚合物注入总量一定的情况下,采用改进算法得到的聚合物驱优化注入方案净现值比均匀注聚方案提高11.64%,使聚合物驱获得更好的技术经济结果.
1 聚合物驱参数优化控制
聚合物驱项目通常采用净现值作为指标对其盈利能力进行技术评价[14],聚合物驱注入参数最优控制就是在控制变量满足约束条件情况下,计算性能指标函数J的最大值及相应的最优控制变量u, 选取聚合物注入浓度和段塞尺寸作为聚合物驱最优控制优化参数.
1.1 指标函数
为科学评价聚合物驱项目的盈利水平,通常采用增量累积净现值作为评价指标,即整个生产周期内各时间段增量净现金流量,按照设定的折现率折成现值后求和所得到的值.其中,各时间段增量净现金流量为增量现金流入量与现金流出量之差.对于聚合物驱项目,现金流入量为相对于水驱的年增原油产量的销售收入,现金流出量为聚合物驱项目生产过程中的投资、生产成本以及税费.据此,可以得到聚合物驱累积净现值的计算公式为
RPo)Qoiα]}×(1-ic)-i-nIs
(1)
其中,J为累积增量净现值(单位:元);Qoi为年增油质量(单位:t);Po为原油价格(单位:元/t);α为原油商品率(单位:%);Cm为每吨油增加操作费用(单位:元/t);Qpi为年注聚质量(单位:t);Pp为聚合物价格(单位:元/t);Rs为资源税(单位:元/t);R为综合税率(单位:%);t为评价时间(单位:年);ic为基准收益率(单位:%);n为区块等效井数(单位:口);Is为单井增加投资费用(单位:元/口).
根据式(1),结合最优化问题的一般数学表达形式,建立聚合物驱注入参数最优控制数学模型为
RPo)Qoiα]}×(1+ic)-i-nIs
(2)
在聚合物驱实施过程中,受注入能力和聚合物价格的影响,对注入浓度和段塞尺寸要实施一定的限制,即控制变量要满足一定的约束条件,边界约束是最常见的约束形式,即
(3)
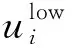
1.2 注入参数优化控制算法
采用单侧差分格式计算FDSA梯度为
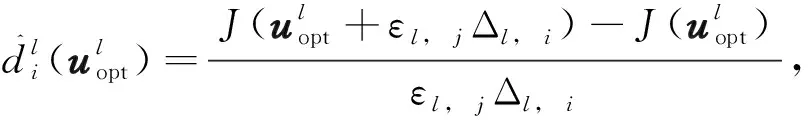
i=1,…,Nu
(4)

由式(4)可知,性能指标函数对控制变量ui和uj的FDSA近似梯度比值为
横店影视职业学院足球选项课课程设置总体情况是课程的目标体系设置不太明确,教学内容和方法没能及时更新。从对高职院校足球选项课课程目标体系的认识来看,横店影视职业学院足球选项课教学对高职院校学生的培养与全国高等学校体育课程指导纲要的精神差距比较大,这与高职院校重技能,轻兴趣和能力以及体育活动。忽略足球带给学生们的成长和健康,忽视学生的锻炼习惯和兴趣的培养有比较大的关系。这种情况不利于学生培养终身体育意识。
(5)
假设SPSA算法中各控制变量采用的扰动步长与FDSA算法取值相同,则性能指标函数对控制变量ui的SPSA近似梯度和FDSA近似梯度之间有如下关系
(6)
取指标函数对控制变量ui和uj的SPSA近似梯度大小比例与FDSA近似梯度大小比例相同,则控制变量ui和uj的扰动步长应满足
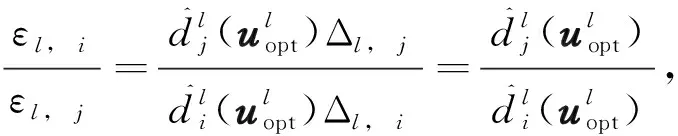
i,j=1,2,…,Nu
(7)
在第l个迭代计算步构造SPSA扰动步长修正矩阵,得到第l个迭代计算步各控制变量的SPSA-FDG近似梯度为

i=1,2,…,Nu
(8)
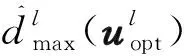
由式(8)可知,当使用SPSA-FDG算法时,如果不进行扰动步长修正,则SPSA-FDG算法为SPSA算法;如果每个迭代步都进行扰动步长修正,则SPSA-FDG算法类似于FDSA算法.因此,SPSA-FDG算法是一类更普适的算法,FDSA算法和SPSA算法为该类算法的两个特例.SPSA-FDG算法梯度估计精度没有FDSA算法高,但高于SPSA算法,同时保留了SPSA算法每次迭代次数少的优点.因此,改进算法的收敛性要好于FDSA算法和SPSA算法,且易于结合油藏数值模拟器求解聚合物驱最优控制问题.
2 实例应用

图1 油藏数值模拟模型Fig.1 Reservoir numerical simulation model
本研究利用SPSA-FDG算法研究聚合物驱最优控制,并将优化结果与FDSA算法、SPSA算法进行对比分析,其中,SPSA算法需要382次油藏数值模拟计算,而FDSA算法由于梯度计算效率低下,迭代收敛时需要多达1 749次数值模拟计算.
SPSA-FDG算法梯度估计精度高于SPSA算法,且具有SPSA算法每次迭代次数少的优点,在达到收敛时仅需要248次油藏数值模拟计算,是这3种方法中总体计算量最小,能较好解决非均质油藏分段塞聚合物驱注采参数优化求解难题.
表1为各优化算法计算得到的聚合物注入质量浓度和段塞尺寸优化结果. 由表1可见,不同优化方法得到的各阶段注入参数变化规律相近,其中聚合物驱前置段塞质量浓度最高,主要起到前缘调剖作用;主段塞及副主段塞质量浓度较高,用量最多,是聚合物驱改善油水流度比,降水增油的关键部分;后置段塞为流度保护段塞,质量浓度最低,用量最少,主要是为了防止后续水驱指进破坏主段塞影响降水增油效果.
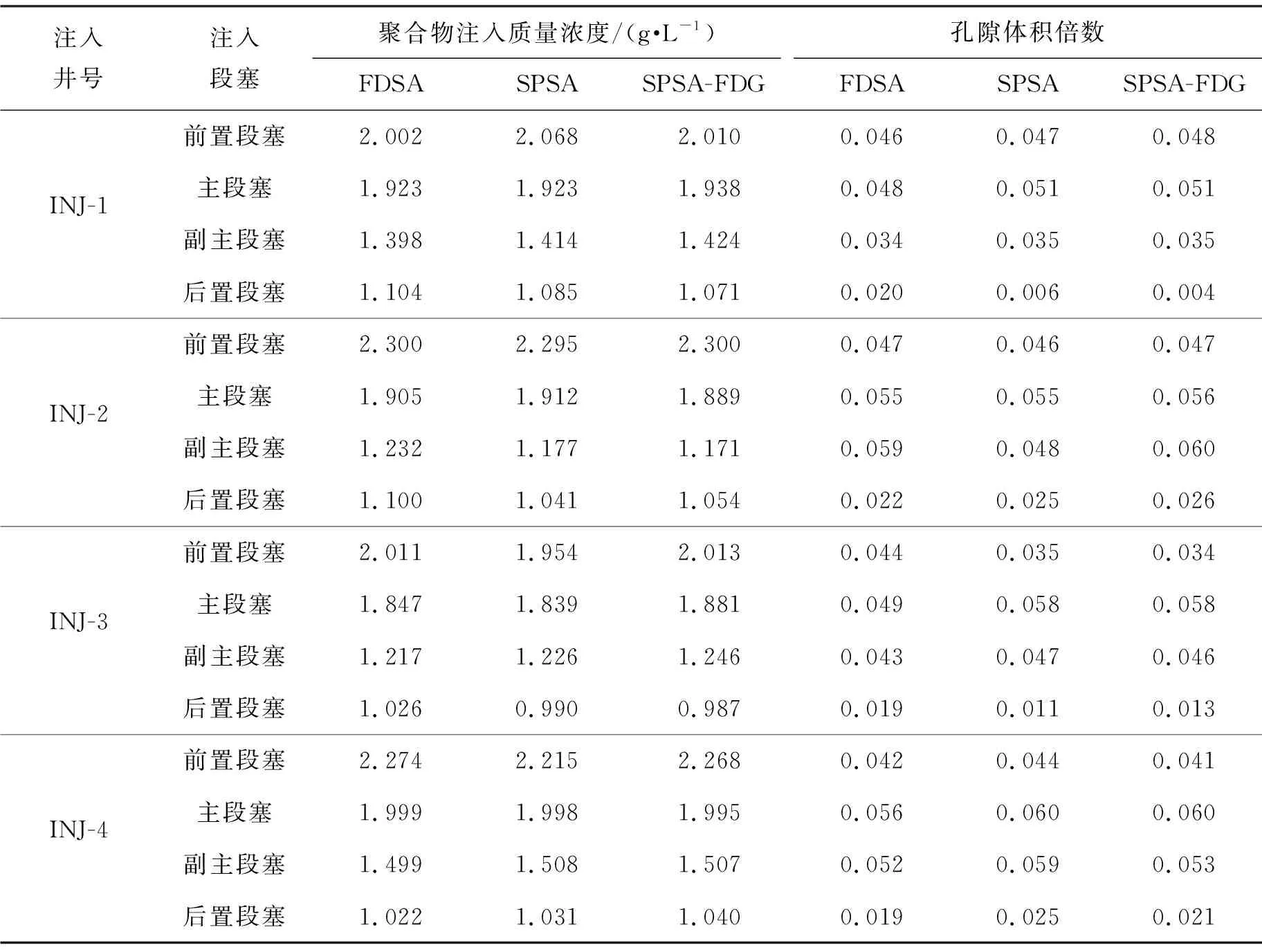
表1 聚合物注入质量浓度和段塞尺寸优化结果
表2为FDSA算法、SPSA算法和SPSA-FDG优化算法计算得到的各注入井聚合物配注量优化结果.由表2可见,在聚合物注入总量一定的情况下,注入井所在井组非均质性强,聚合物配注量大;若注入井所在井组非均质性弱,则应适当减少聚合物配注量.为对比分析各单井聚合物优化配注对聚合物驱总体开发效果的影响,聚合物注入总量与SPSA-FDG算法优化结果相同(1.123V), 均匀设计了各单井的注聚方案[17],采用单段塞方式注入,图2为算法优化注聚方案与均匀注聚方案计算得到的油藏含水率及累积采出程度变化曲线.由图2可见,采用由优化算法计算得到的优化方案进行聚合物驱开发时,在聚合物注入总量一定的情况下,聚合物驱见效时机提前,含水下降漏斗加深1.86%,累积采出程度提高0.3%,开发效果变好.分析认为经优化后,非均质性较强的井组因配入量增大而增加的产油量大于非均质性较弱的井组因降低相应注入量而减少的产油量,使油藏总体采出程度得到提高.图3为SPSA-FDG优化注聚方案与均匀设计注聚方案计算得到的聚合物驱净现值随开发时间变化的关系曲线.由图3可见,在聚合物注入总量一定的情况下,采用由SPSA-FDG算法得到的优化方案更早获得聚合物驱开发经济效益,经济净现值比各单井均匀注聚方案提高11.64%.
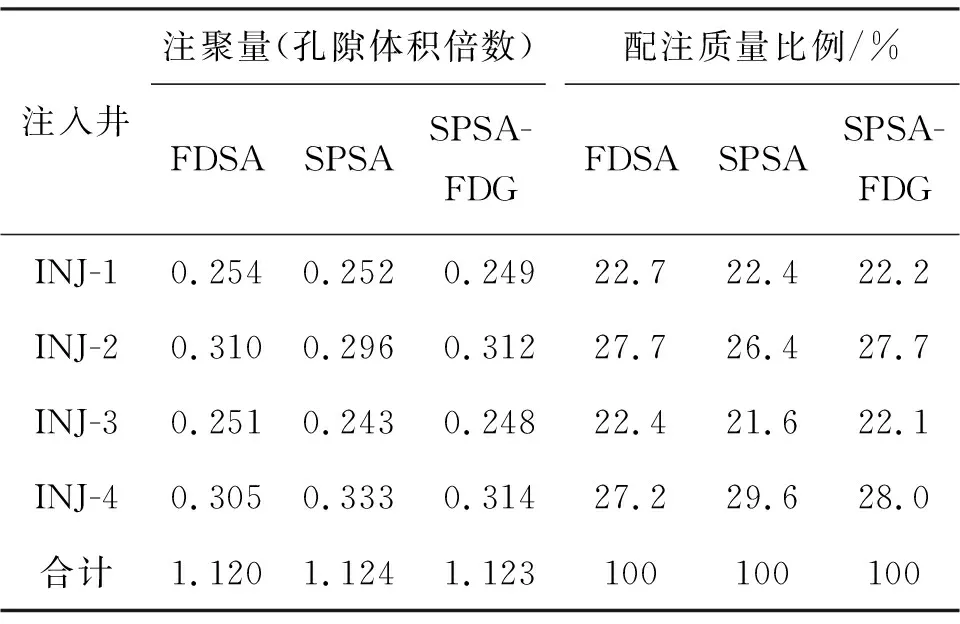
表2 注入井聚合物配注量优化
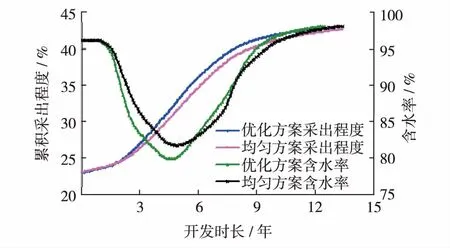
图2 含水率及累积采出程度变化曲线Fig.2 Water cut and cumulative oil recovery curve

图3 经济净现值变化曲线Fig.3 Economic net present value change curve
3 矿场应用
将优化注聚方案于2015年7月应用于某油田实际井组注聚,效果较为明显:日净增油最高达到64 m3,井组综合含水平均下降3.5%.根据优化方案实施前后水驱特征曲线可以评价注聚井组优化方案的增油效果,见图4.优化方案实施后特征曲线斜率向下发生了偏折,表明优化方案实施后注聚井组开发效果逐渐趋好.
井组丙型水驱特征曲线表达式为
(9)
其中,Lp为累计产液体积;Np为累计产油体积.由式(9)计得实施优化方案实现累计增油15 799 m3,累积采出程度提高0.36%.通过以上实际动态计算指标与优化计算指标对比,验收了本优化算法的可靠性.
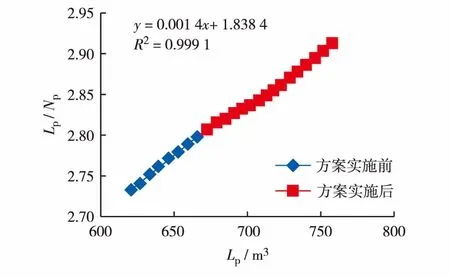
图4 丙型水驱特征曲线Fig.4 Water drive type curve (III)
4 结 论
1)本研究基于FDSA和SPSA算法,推导建立了更普适的SPSA-FDG算法,FDSA算法和SPSA算法为本算法的两个特例.
2)算法保留了SPSA算法每次迭代数值模拟计算次数少的优点,但梯度估计精度高于SPSA算法,收敛性好于SPSA算法,达到收敛时油藏数值模拟计算最小,较好地解决了非均质油藏分段塞聚合物驱注采参数优化求解难题.
3)在聚合物注入总量不变条件下,采用本算法得到的聚合物驱优化注入方案净现值比均匀设计注聚方案采收率值提高11.64%,明显提高了非均质油藏聚合物驱的技术经济结果.
