市道轮换下的高频数据参数估计

柳向东，靳晓洁

暨南大学经济学院，广东广州 510632

20世纪90年代以前，金融市场的研究多以低频数据为依据，低频数据是指日、周、月、季度及年的频率数据. 近年来，随着计算机与通信技术的迅猛发展，记录高频数据日趋便捷，从而受到金融界的广泛关注. 高频数据是指金融市场运行过程中以小时、分钟、秒或实际交易间隔为采集频率的日内交易数据. 金融市场往往是连续运行的，交易频繁，市场情况瞬息万变，基于低频数据的金融市场研究无疑会损失大量有效市场信息，无法准确理解市场微观结构. 而高频数据所包含的资产价格信息接近于理论上连续时间的资产价格信息，不仅包含金融资产价格更丰富的信息，还包括像交易时间间隔、交易量、买卖价差等众多其他维度的信息，能够对金融市场进行更精细的分析，对理解市场微观结构具有重要作用. 结合金融学、计量经济学、时间序列分析及统计学等理论，不少学者从不同角度对高频数据进行了大量的金融计量研究. 朱建平等[1]对国内外金融高频数据的研究现状进行剖析，澄清金融高频数据的概念与特征，从统计学视角审视金融高频数据. 雷井生等[2]利用改进的统计套利策略对高频数据进行研究，满足了机构投资者套利需求，同时引进一种更有效的全新投资方式. HANSEN等[3]提出一种分析高频数据的新模型，即已实现测度与传统自回归条件异方差(generalized autoregressive conditional heteroskedasticity，GARCH)模型相结合的Realized GARCH模型，且通过实证表明，与基于低频的数据日收益率的一般GARCH模型相比，其有实质性的改进. 王天一等[4]考察Realized GARCH模型用于高频数据的研究，着重考察了沪深300指数1 min高频数据的收益率分布及波动率预测，指出不同抽样频率的已实现方差对模型预测有显著影响. ZHANG[5]提出利用幂律函数的霍克斯过程(Hawkes processes with power-law kernels)对高频数据进行建模，且通过与其他模型对比，表明此模型有实际应用价值. 李胜歌等[6-11]也对高频数据的波动率进行研究，利用一阶偏差修正方法、ARFIMAX模型、GARCH模型、SV模型、ACD模型、ACH模型、扩展的ACH模型以及跳扩散模型等对高频数据进行了分析. 近年来，对于高频数据的实证研究结果表明，金融市场存在资产价格跳跃行为. 沈根祥[12]构造了跳跃行为的Hausman检验统计量，并对沪深300指数高频数据进行分析，发现样本区间内有1/3以上的交易日存在跳跃行为. 唐勇等[13]基于非参数方法，结合A-J跳跃检验统计量，构建新的跳跃方差和连续样本路径方差对上证综指高频数据进行建模分析，包括高频数据中跳跃方差统计特征、跳跃方差贡献、跳跃幅度以及跳跃与经济信息关系，有助于投资者优化投资策略，为监管部门提供监管依据. BAJGROWICZ等[14]则在对高频数据分析中，利用伪跳跃(spurious jump)检验法研究跳跃，认为跳跃发生与流动性压力有关. 汪先珍[15]基于BN-S理论框架对上证综指高频数据进行研究，证实跳跃的存在，进而剥离出股价行为中的跳跃成分,并对跳跃产生的时刻、幅度以及分布特征加以分析,着重探讨了几个跳跃个例产生的原因.

从上述文献来看，对高频数据的研究并不少见，但利用马氏市道轮换研究高频数据的文献并不多. 马氏轮换模型可以刻画金融市场的各种状态，对股票价格波动的描述更加切合实际，因此，在马氏轮换基础上推导各类具体模型对于高频数据的分析预测具有重要现实意义．近年来，国内外许多学者将马氏轮换运用到金融市场模型中，并得到较好的结论. HAMILTON[16]首先提出马氏市道轮换,并利用该模型对时间序列的对数差分数据进行回归模拟，较好地刻画了实际产出增长的非线性动态和非对称特性. CAI等[17-18]将马氏市道轮换引入ARCH模型，为存在结构转换的金融资产序列的波动性建模提供新方法. 佟杰[19]在预测模型中引入马氏轮换，并用Baum Welch算法和弗罗贝尼乌斯范数最小法进行参数估计，并预测上证指数收益率，得到很好的预测效果. 刘金全等[20]在CKLS中加入马氏轮换，将传统CKLS模型推广至更为一般的状态相依模型，并通过Hamilton滤波和Kim平滑概率得到比传统CKLS模型更好的估计和分析结果. 杨宝臣等[21]针对SHIBOR动态特性中存在的状态转换和波动聚类现象，分别将马氏轮换和GARCH效应引入CIR模型，基于Kim滤波的极大似然估计法进行估计,并与CIR模型对比，发现改进的模型对风险溢价动态特性的刻画能力更强. 本研究尝试在马氏市道轮换下对高频数据进行研究. 高频数据选用上证综指每5 min收盘价作为分析，并用市道轮换下的自回归模型以及波动率替代模型对高频数据进行分析，其目的是由于在不同经济体制下会产生不同收益率，而马氏轮换能对这些不同经济体制进行明确研究. 在估计技术方面，本研究采用极大似然法，并结合Hamilton滤波概率和Kim平滑概率等来估计马氏市道轮换模型，取得较精准的预测效果. 本文还将市道轮换模型加入到波动率替代模型对高频数据进行分析，并给出了相应的估计.

1 高频数据模型

1.1 基本知识

定义1一个离散的随机过程{St,t∈N}被称为马尔可夫链，若对所有t∈N，满足

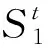
定义2在t时刻的n步转移概率定义为aij(n,t)=P(St+n=jSt=i)， 即过程在t时刻位于状态i， 在t+n时刻转移到状态j的概率.

值得注意的是，若马尔可夫链在t时刻的n步转移概率aij(n,t)与t无关，则称为齐次马尔可夫链. 此时n步转移概率记为aij(n)， 而1步转移概率简称转移概率，记为aij， 下文中马尔可夫链均指齐次马尔可夫链，转移概率aij均指1步转移概率.

定义3双离散随机过程{St,t∈N}、 {Yt,t∈N}被称为隐马尔可夫链，若满足

P(St=stSt-1=st-1)；

P(St=stSt-1=st-1)；

P(Yt=ytSt=st)；

P(Yt=ytSt=st).

其中， {St}称为状态过程，不可观测，实际上是一个齐次马尔可夫链； {Yt}是观测值过程. 以上性质可见，给定St-1，St与其他所有变量(过去的观测值和过去的状态)均无关，给定St，Yt与其他所有变量(之前和之后的观测值、过去的状态)均无关. 这些性质是下文中经常用到的性质.

引理1P(ABC)=P(AC)P(BAC)

引理1虽然是一个很简单的公式，但在下文许多公式的推导中却频繁使用.

1.2 马氏市道轮换自回归模型

近年来，各种经济事件序列已作为市道轮换事件序列进行建模. 建模中，该变量的分布被假设在一个特定的市道或状态条件下发生. 会产生一系列重大变化. 经典的自回归模型要求时间序列平稳，但实际中平稳性往往难以满足. 金融模型的不稳定性可视为时间序列出现结构性的变化，即不同数据后面隐藏着不同状态，而引入市道轮换的自回归模型MS-AR (Markov switching model autoregressive model)可以解决这一难题[22]. 下面以一阶市道轮换自回归模型MS-AR(1)为例进行介绍.

yt-μSt=β(yt-1-μSt-1)+εt

(1)

其中，St是t时刻未知市道或者状态，本研究中只考虑两种市道的情况，即

(2)

ytSt-1=i，St=j,

(3)

其中， Ft={y0,y1,yt}， Ft指截止到时刻t所拥有的观测值yt的所有信息，称为信息集或域流. {yt}和{St}即为隐马尔可夫链，可见其满足1.1节所述性质.

估计模型的参数采用极大似然方法，因此，求得似然函数的表达形式是最重要的一步. 考虑{y1,y2, …,yT}的似然函数f(y1,y2, …,yT)， 反复利用引理1可得

具体证明不再赘述，由此式可知求得f(ytFt-1)的表达式即求得了似然函数的表达式，因此，以下主要围绕求f(ytFt-1)的表达式展开.

P(St-1=i,St=jFt-1)]

为方便起见定义

ηi, j(t)=f(ytSt-1=i,St=j, Ft-1)；

γi, j(t)=P(St-1=i,St=jFt-1).

则下式成立

(4)

由于市道St不可观测，只能通过计算St在不同时期的取值概率来推测St的取值，推断概率方法包括：事前概率、Hamilton滤波及Kim平滑概率.

事前概率指基于t-1时刻信息集Ft-1对t时刻的市道进行推断的条件概率，记为Pit，

Pit=P(st=iFt-1)

Hamilton滤波概率指基于t时刻信息集Ft对t时刻的市道进行推断的条件概率，记为εi(t)，

εi(t)=P(St=iFt)

这里εi(0)=P(S0=i)=πi. 其中，πi为{St}位于状态i的初始分布，i=1,2.

Kim平滑概率是基于所有信息对t时刻的状态进行推断的条件概率，记为ρj(t)，

ρj(t)=P(St=jFT)

γi, j(t)=P(St-1=i,St=jFt-1)的计算过程分为预测和更新两个过程，设初始为εi(0)=πi， 具体过程为：

1) 预测.

γi, j(t)=P(St-1=iFt-1)P(St=jSt-1=i, Ft-1)=P(St-1=iFt-1)P(St=

jSt-1=i)=εi(t-1)aij

(5)

2)更新.

P(St-1=i,St=jFt)=P(St-1=i,St=

(6)

记κi, j(t)=P(St-1=i,St=jFt), 在t时刻yt被观测到后，信息集Ft-1被更新到Ft={Ft-1，yt}，此时，κi, j(t)相当于γi, j(t)的更新，即γi,j(t)更新为

(7)

当完成一轮预测和更新后，即完成式(5)至式(7)的计算后，可计算滤波概率，即式(8). 然后继续开始新一轮计算.

(8)

当上述全部完成时，可计算有对数似然函数，用κi, j(t)代替γi, j(t)， 有对数似然函数为

(9)

1.3 马氏市道轮换波动率替代模型

由于日内数据可以记录到很高频率的交易数据,日均大约几千个数据，此时记录之间的时间间隔已非常小，所以，对于高频数据的建模，自然的想法是利用连续时间模型，连续时间金融理论主要是考虑使用半鞅过程来刻画价格或者收益率的变动过程. 考虑金融资产的连续时间对数价格过程(或者对数收益率过程){Y(u) }， 称其是一个半鞅，若有如下分解：

Y(u)=A(u)+M(u)

其中，过程{A(u)}是一个有界变差的过程； {M(u)}是一个局部鞅. 连续时间金融理论中使用半鞅的原因在于，只有在半鞍上才能定义随机积分[22]. 它被广泛用于衍生品(期权，期货及债券)的定价中，对于半鞅而言，一般用它的二次变差过程衡量其波动性. 二次变差QV可被定义为已实现方差随抽样频率趋于无穷的概率极限，

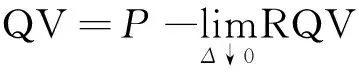
BOLLERSLEV[23]提出的广义GARCH模型，因为能很好的解释波动率汇聚和收益率厚尾等现象，已成为研究和预测时变波动率的标准工具. GARCH模型通常用于低频数据，如日、周、月数据，高频数据包含更丰富的信息，而与高频数据相结合成为一个重要的方向. 为使GARCH模型与日内的高频数据结合发挥模型优势，VISSER[24]提出基于GARCH模型的尺度模型和波动率替代模型，将日内的高频数据嵌入到模型的框架中，且指出通过构造合适的波动率替代，可以改进模型的伪极大似然估计的渐近方差.考虑日内对数收益率Rt(u), 日内波动率可以被已实现波动率RVt代替. 下面介绍尺度模型和波动率替代.

(10)

(11)

其中，ψt(u)服从均值为0、方差为1的标准分布； {ψ0(u)，ψ1(u)，…}独立同分布. 两者为尺度模型.Rt(0)为隔夜收益率，而Rt(1)即rt， 故当t=1时，尺度模型即转代为GARCH(1，1).

VISSER[24]定义了替代波动率的统计量，称为波动率替代. 一般地，称随机变量Ht≡H(Rt(·))为波动率替代，如果H为正且满足正齐次性，则H(sRt(·))=sH(Rt(·)),s≥0

波动率替代一般有rt， 日内最高-最低价差、已实现波动率等.

(12)

记μH=E(H(ψt(·)))， 0≤μH<∞，τH=τ(μH)2，ZH, t=H(ψt(·))/μH， 则

(13)

(14)

伴随经济政策的出台和金融市场监管制度的变迁自身完善，在一个不成熟的金融市场上，马氏轮换是一个普遍存在的现象，对这种结构性变换的描述是必要的[25]. 而GRAY等[26-27]在GARCH方程中引入马氏轮换，建立MRS-GARCH模型，利用滞后的条件方差取期望值,从而避免了路径依赖问题，通过检验表明MRS-GARCH模型较传统的GARCH模型在拟合和预测能力上均有提高. 由于尺度模型和波动率替代模型是在GARCH模型基础上提出，因此，很自然考虑到在这两个模型上加入马氏市道轮换. 这里首先对尺度模型(10)和(11)加入市道轮换，即

(15)

(16)

由式(12)知H具有齐次性，用式(12)所述H作用于式(15)，由齐次性即可得到马氏市道轮换波动率替代模型

(17)

(18)

将马氏轮换引入GARCH模型后存在严重的路径依赖问题，即t时刻的条件方差将依赖于所有变量t时刻之前全部时刻的取值及其状态. 当样本较大时，这使模型异常复杂难以估计. 同样，将马氏轮换引入波动率替代模型也存在路径相依问题，因此，可模仿MRS-GARCH的估计方法. GRAY[26]利用一期条件方差的期望值代替条件方差本身，从而解决了一模型中存在的路径依赖问题. 此后，KLAASSEN[27]充分利用信息，进一步改善模型. 本研究所使用方法，正是基于KLAASSEN所提出的方法. 具体来说，式(14)中等号右边条件方差项的表达式为

(19)

(20)

为方便计算εj(t)， 引入符号ηjt， 即

εj(t)=P(St=jFt)=P(St=jFt-1,Ht)=

(21)

Pit=P(St=iFt-1)=

(22)

P1tη1t+P2tη2t

(23)

由上式迭代可得出似然函数L

(24)

2 模型实证研究

选用2017-01-03 09∶35至2017-08-02 14∶55上证综指每5 min的收盘价格数据作为研究对象. 为方便观察和分析，将收盘价缩小100倍，调整后的收盘价时序和直方图见图1和图2.

图1 收盘价时序图Fig.1 Closing price sequence diagram

图2 收盘价直方图Fig.2 Closing price histogram

图3为收益率的时序图. 可见，收益率在固定范围内变化，同时波动率存在聚集性，即大的波动率后面常常伴随较大的波动率，小的波动率后面也常常伴随小的波动率. 统计分析得出上证综指每5 min 收盘价的基本分析结果如表1. 可见，收盘价在30 元. 在22～33.05 元(收盘价缩小100倍之后的价格)内波动，平均价格为31.80 元.

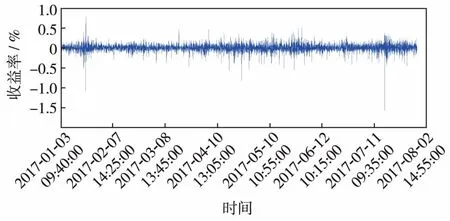
图3 收益率时序图Fig.3 Return sequence diagram

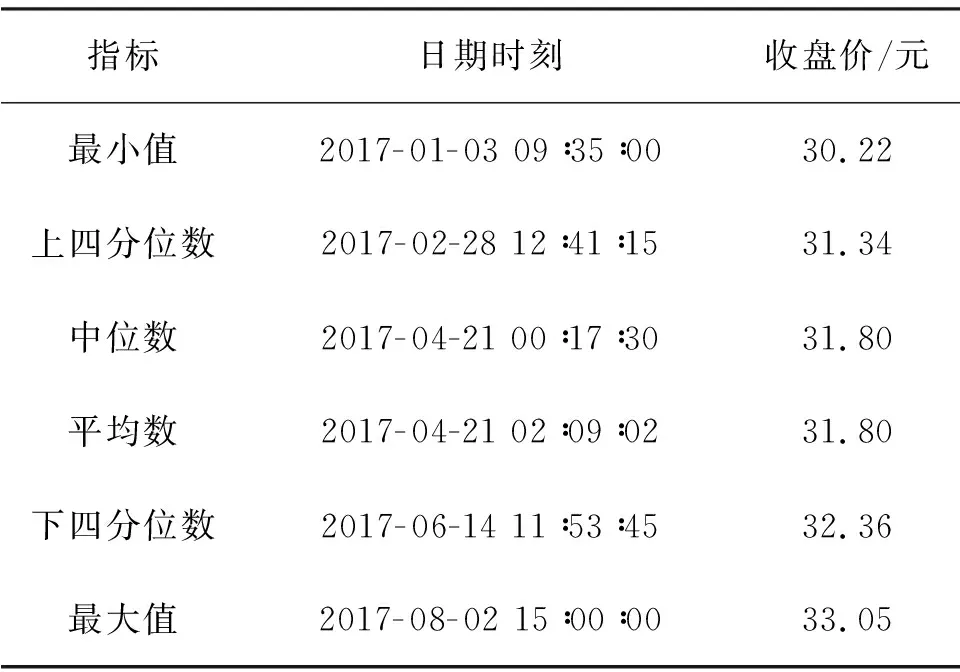
指标日期时刻收盘价/元最小值2017-01-03 09∶35∶0030.22上四分位数2017-02-28 12∶41∶1531.34中位数2017-04-21 00∶17∶3031.80平均数2017-04-21 02∶09∶0231.80下四分位数2017-06-14 11∶53∶4532.36最大值2017-08-02 15∶00∶0033.05

另外， LB检验结果显示p-value < 2.2×10-16，拒绝原假设，收盘价序列不是白噪声，因此，有分析价值；ADF检验结果表明，检验统计量值为-1.848 2，大于显著性水平0.05下的分位数-2.86,则收盘价序列非平稳，而马氏市道轮换转换模型可解决这一问题.

首先，用MS-AR(1)模型对高频数据进行分析. 这里高频数据的需要估计参数向量为θ=[μ1，μ2，σ1，σ2，β，p,q].

使用Hamilton滤波算法计算似然函数，进行极大似然估计，得出参数的极大似然估计值如表2. 分析可见，熊市为市道1，牛市为市道2，熊市均值为30.499 0 元，标准差为0.049 0；牛市的均值为30.527 0，标准差为0.008 4. 均值均在收盘价区间内，且熊市的标准差比牛市的大，这说明熊市价格震荡幅度更大.

由此可见，牛市转换成牛市的概率高，即牛市的第2天还是牛市的概率更大，熊市转换成牛市的概率也很大.

表2 MS-AR(1)参数估计 1)

1)该统计日期同表1

下面进行市道解码，即把2017-01-03至2017-08-02上证综指每5 min收盘价的市道推断出来，采用Kim平滑概率，市道即对应平滑概率较大的状态；滤波概率和平滑概率见图4和图5.

图4 滤波概率图Fig.4 (Color online) Filter probability figure

图5 平滑概率图Fig.5 (Color online) Smoothing probability figure

为看清楚高频数据状态预测之间的变化，选取了2017-04-24的数据，如图6. 可见，高频数据之间存在明显的市道转换.

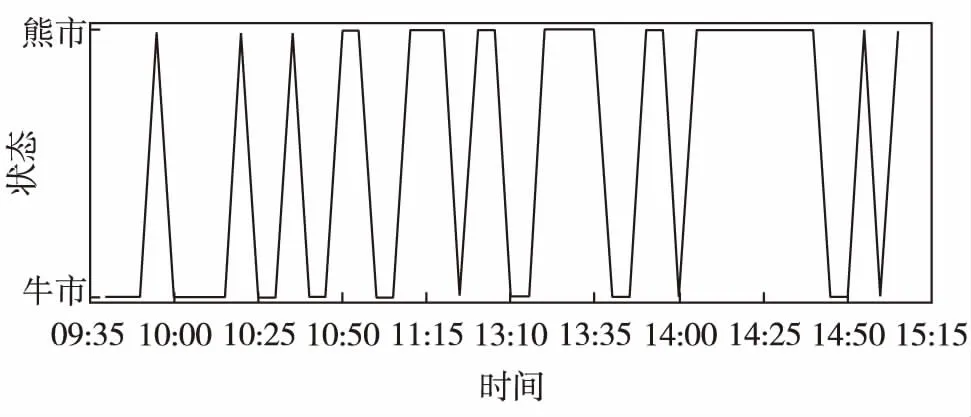
图6 状态转换图Fig.6 Regime switching figure

为评价模型的预测效果，引入平均相对误差ARPE为

通过评估可知，预测价格与真实价格之间的平均相对误差为 7.493 2×10-4，平均相对误差较小，说明预测效果相对较好，为清楚地看到预测效果，只选取2017-08-01至2017-08-02内收盘价作预测图，见图7.

图7 收盘价预测图Fig.7 (Color online) Closing price forecast figure

这里给出2017-08-02 15∶00的点预测，此时真实价格为32.850 6元，模型预测价格为32.818 3元，预测的标准差为0.016 9元，效果比较理想.

下面对高频数据进行波动率研究，从2017-01-04上证综指的日内数据开始. 5 min高频数据对于进行波动率研究是合理的. 唐勇[28]以上证综指高频数据为例，实证了5 min抽样频率数据的合理性. LIU等[29]研究了超过400种不同的波动率估计量，实证发现，至少在统计意义上很难显著地击败以5 min 抽样数据所估计的波动率.

极大似然估计参数如表3. 可见，状态2时波动率较大，状态1时波动率较小，且高波动率之后依旧是高波动率的概率较大.

表3 波动率的参数估计 1)

1)与表1、表2统计日期一致

结 语

高频数据不仅丰富了金融资产价格信息，而且还包含众多其他维度的信息，如交易时间间隔、交易量及买卖价差等，这些可以对金融市场进行更精细的分析，对于理解市场价格形成和信息的传递机制等市场微观结构方面的特征，具有相当重要的作用. 本研究通过市道轮换对高频数据进行分析研究，包括市场价格和波动率两部分，发现日内数据中存在市道轮换，并对市场价格未来做了比较准确的预测，贴近事实，吻合市场. 同时模型参数少，简洁实用，可操作性强，可为市场投资策略提供参考和指导. 在本研究的后半部分，尝试用市道轮换下的波动率替代模型研究高频数据的波动率，并给出分析模型和方法. 未来研究可尝试通过改进市道轮换下的波动率替代模型对高频数据的波动率进行进一步的估计和预测，并且尝试研究超高频数据. 另外，半马氏能够克服马氏轮换过程一些缺点，如无记忆性[30-32]，未来可以把马氏市道轮换下的高频数据模型推广到半马氏的情形，同时讨论带跳的估计问题.