基于弱派系的多层社会网络重叠社团发现算法

张月霞，杨瑞琪，康 劲

北京信息科技大学信息与通信工程学院, 北京 100101

社团发现是复杂网络研究中的一个重要问题．现实生活中人们通常会使用多种社交工具进行日常交流与活动，这些不同的社交网络与用户构成了一个多层社会网络[1]，该网络中通常存在一些隐藏的社团结构，其中的用户往往会有更加紧密的联系与接近的兴趣．复杂网络中的社团通常分为非重叠社团与重叠社团，非重叠社团中节点有且仅属于一个社团，而重叠社团中节点可属于多个不同社团，现实中的用户一般会同时存在于多个社团之中，重叠社团较为接近真实情况[2]，多层社会网络中的重叠社团发现，逐渐成为复杂网络中的一个研究热点．研究社会网络中的社团有利于分析信息传播与舆论传播等问题，因此对社会网络中社团发现的研究具有一定的现实意义．

目前，学者们对多层社会网络与多层图中的社团发现算法已有了一些研究．FAN等[3]使用局部社团检测和根据相似度合并多层社团的方法进行多层社会网络的社团发现；CHEN等[4]将复杂网络中的连接分解为多维结构，使用FN(fast Newman)算法构建兄弟矩阵挖掘网络中隐藏的社团结构；GLIGORIJEVI等[5]通过改进非负矩阵分解的方法对多层图进行融合与聚类来发现社团结构；PIZZUTI 等[6]将模块化度作为目标函数结合多目标优化算法检测多层网络中的社团．

也有学者使用不同的方法来挖掘复杂网络中的重叠社团．JIANG等[7]将社会网络中的异质信息融合构建用户邻接图，并执行多标签传播来发现有效社团；SU等[8]使用结合局部聚类系数的种子集扩展方法挖掘社交网络中的重叠社团；HUANG等[9]结合集成学习与粒子群优化算法避免结果中冗余的小型社团；ZHANG等[10]提出了一种基于弱派系的算法，解决了传统派系过滤算法应用于大规模网络时复杂度高的问题；ZHANG等[11]使用基于混合表现的多目标进化算法检测复杂网络中的重叠社团．虽然不少学者在多层网络社团发现和重叠社团发现上做了很多研究，但针对多层社会网络和重叠社团的社团发现算法较少，且现有算法较难检测出小型网络中的社团．

本研究提出一种基于弱派系的多层社会网络重叠社团发现算法(weak clique based community detection algorithm, WC-CDA)，利用弱派系细粒度的特性，挖掘网络中更小的社团结构，并同时支持无向与有向网络．通过检测不同社会网络中的弱派系，挖掘用户在不同场景下的隐含关系，进一步合并不同网络的弱派系来得到多层社会网络中的重叠社团结构．

1 相关知识

1.1 多层社会网络与重叠社团

目前的多层或多维社会网络[3-4，6]中，重叠社团发现的一般步骤是先检测不同层或不同维度网络的重叠社团，再对检测结果进行融合，最终得到划分结果．

1.2 基于局部社团的多层在线网络重叠社团发现算法

FAN等[3]提出的基于局部社团的多层在线网络重叠社团发现算法(local community based community detection algorithm, LC-CDA)是一种较新的多层社会网络重叠社团发现算法．该算法步骤为

1)检测每层网络中的局部社团，对于网络中的每个节点，将其与邻居节点划分进局部社团c中， 对于c中的每个节点，计算其社团内和社团外节点连接数的差值，即

(1)

其中，若节点i与节点j之间有连接，则aij=1．

3)计算所有局部社团中两两的重叠系数(ci∩cj)/min{ci,cj}， 与阈值β(0<β<1)进行比较，若大于阈值则对两个局部社团进行合并，得到社团划分结果．

LC-CDA算法将根据数据集中喜好信息所划分的社团结果作为正确结果，并与算法所划分的社团结果进行比较，即通过式(2)计算两种结果的相似度对算法进行评价．

(2)

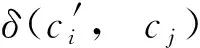
(3)

S的取值范围是[0, 1]．S值越大，表示该算法所划分的社团与使用喜好信息划分的社团越接近，算法性能越好．

该算法中局部社团仅考虑了社团整体与外部的联系，未考虑社团内部节点间的拓扑属性，因此无法发现更多细粒度的小社团，且经本研究实验发现，LC-CDA用于小型多层社会网络时，很难有效地检测出多个重叠社团结构．为此，本研究提出一种基于弱派系的多层社会网络重叠社团发现算法．

2 多层社会网络重叠社团发现算法

WC-CDA首先计算不同社会网络层的弱派系，然后将这些弱派系根据相似度进行合并，得到社团划分结果，最后通过综合考虑节点度和邻居连接属性的弱派系来发现小型网络中的社团结构．

2.1 弱派系

在一个网络G=(V,E)中，其中V为节点集合，E为节点间的边集合，假设u和v是G中的两个相邻节点，则由节点u和v所决定的弱派系定义为

Guv=(Vuv,Euv)

(4)

其中，Vuv={u,v}∪{Nu,Nv}，Vuv分别为节点u和v及其邻居节点构成的节点集合，Nu和Nv为节点u和v的邻居节点集合；Euv={(x,y)∈E}x，y∈Vuv}，Euv为Vuv中节点间属于边集E中的连边所构成的边集合．节点u和v分别通过计算节点优先级与节点相似度得出．

2.2 节点优先级

在一个网络G=(V,E)中，其中，V为节点集合，E为节点间的边集合，假设u为G中的一个节点，则节点u的优先级定义为

(5)

其中，mu为节点u的所有邻居节点之间的边数；k为节点u的度．对于有向图，使用节点u的入度计算优先级Pu， 即

(6)

其中，mu为节点u的所有邻居节点之间的边数；kin为节点u的入度．

式(5)与式(6)综合了仅考虑节点度的度中心性，与仅考虑邻居节点连接数量的局部聚类系数．两个公式同时利用了度与邻居节点间的连接数，有利于估计节点邻居间连接的紧密程度，优先级越大则表明节点邻居间的连接越紧密．

选择网络中优先级最大的节点作为构建弱派系中的一个节点，另一节点是与优先级最大节点的邻居节点中相似度最大的节点．

2.3 节点相似度

在一个网络G=(V,E)中，其中V为节点集合，E为节点间的边集合，假设u和v是G中的两个邻接节点，则这两个节点的相似度定义为

(7)

其中，Nu和Nv分别为节点u和节点v的邻居节点集；Nu和Nv分别为集合Nu和Nv中的元素数．本算法中计算节点相似度采用的是Slaton指标[14]，在基于共同邻居的相似性指标中，常用的还有Jaccard指标[15]和Sorenson指标[16]等．

2.4 弱派系相似度

在一个网络G=(V,E)中，其中，V为节点集合，E为节点间的边集合，假设C1和C2是G中的两个弱派系，则定义弱派系C1和C2间的相似度为

(8)

对于弱派系C1和C2， 有0≤SCC1C2≤max(V(C1),V(C2))． 对于一个网络中的弱派系设置相同的阈值β， 若两个弱派系的相似度大于阈值时则合并为一个社团，因此本算法也具有可调重叠社团相似性的特点．文献[10]提出的相似度计算考虑到了两者共同的节点与边，而本算法仅考虑共同的节点以便合并多个网络层的弱派系．

2.5 评价指标

社团划分结果的评价指标一般有归一化互信息(normalized mutual information，NMI)[17]指标与调整兰德系数(adjusted Rand index，ARI)[18]指标等．由于大多数真实网络数据集无事先标记好的社团划分结果，因此无法使用这两种指标进行评价．对于未知结果的重叠社团评估，目前主要使用扩展模块化度Qov[19]， 即

(9)

其中，A为网络的邻接矩阵；Ci为一个社团(1≤i≤l，l为社团个数)；m为网络的边数；Qv为节点v所属社团个数；kv为节点v的度．Qov越大表明社团划分的效果越好．

式(9)并不适用于多层网络社团的划分，考虑到网络密度与连边数对社团发现的影响，将网络的边数比例作为网络权重，构建新的指标Qmov， 用于评价多层社会网络重叠社团划分结果．Qmov值越大表明社团划分结果越好．

定义多层网络重叠社团的评价指标Qmov为

(10)

其中，Qi为第i层网络的扩展模块化度；wi为第i层网络的权重，定义为

(11)

其中，Ei为第i层网络的边数．

从式(11)可见，网络边数比例越大，即相对网络密度越大，则模块化度的权重越大．

2.6 算法步骤

算法的输入为多层社会网络Gml和相似度阈值β， 输出为社团集合S， 具体步骤为：

1) 初始化S， 设定阈值β， 输入多层网络数据，对每一层网络G执行步骤 2)至步骤 4)，得到弱派系结果，然后执行步骤5)．

2) 初始化弱派系集合WC．

3) 根据式(5)或式(6)计算当前网络G中所有节点的优先级， 并选取优先级最大的节点u， 根据式(7)计算节点u的邻居节点中与u相似度最大的节点v， 使用节点u与节点v根据式(4)构建弱派系wc并保存至WC．

4) 将步骤 3)中弱派系wc的节点从G中移除，若G中节点非空则回到步骤3)；

5) 根据每一层的弱派系结果构建弱派系集合WClique，并将所有弱派系标记为未访问，对WClique中的所有弱派系执行步骤 6)至步骤8)．

6) 若所选的弱派系C1未被访问，则执行步骤 7)，否则选择下一个弱派系执行步骤 6)至步骤8)；

7) 将C1标记为已访问，对与弱派系C1有重合节点的弱派系集合N(C1)中的弱派系执行步骤8)．

8) 计算弱派系C1与邻居弱派系C2的相似度，将C2标记为已访问．若大于β则合并为一个社团，保存检测出的社团至社团集合S中，否则，不进行合并．

9) 返回社团集合S．

3 仿 真

3.1 数据集

本研究采用tailorshop、AUCS和FF-TW-YT三种真实的多层社会网络数据集进行仿真实验，如表1．其中，tailorshop数据集是由KAPFERER[20]收集的服装厂内39名员工工作与朋友关系的双层网络数据；AUCS数据集是由ROSSI等[21]收集的某大学61名雇员不同线上线下关系的网络数据，该数据集分为lunch、facebook、coauthor、leisure和work五层，均为无向无权网络；FF-TW-YT数据集是由MAGNANI等[22]采集的500名用户在多个在线社交网站上的关系网络数据，每个用户都拥有多个不同社交网站的账号，并在每一层具有不同关系网．该数据集包含FriendFeed、Twitter和YouTube三层，且均为无权网络，其中FriendFeed与Twitter层为有向网络，YouTube层为无向网络．

表1 多层社会网络数据集

3.2 结果与分析

为评估WC-CDA的有效性，将其与LC-CDA比较．两种算法的执行顺序都是先检测单层网络的结果，然后根据β进行社团的合并，通过比较不同相似度下社团发现结果的属性与评价指标来进行评估．由于LC-CDA所用的评估方法只适用于已有结果的数据集，不具有通用性，因此，本研究在仿真过程中使用Qmov指标对两种算法进行评价．

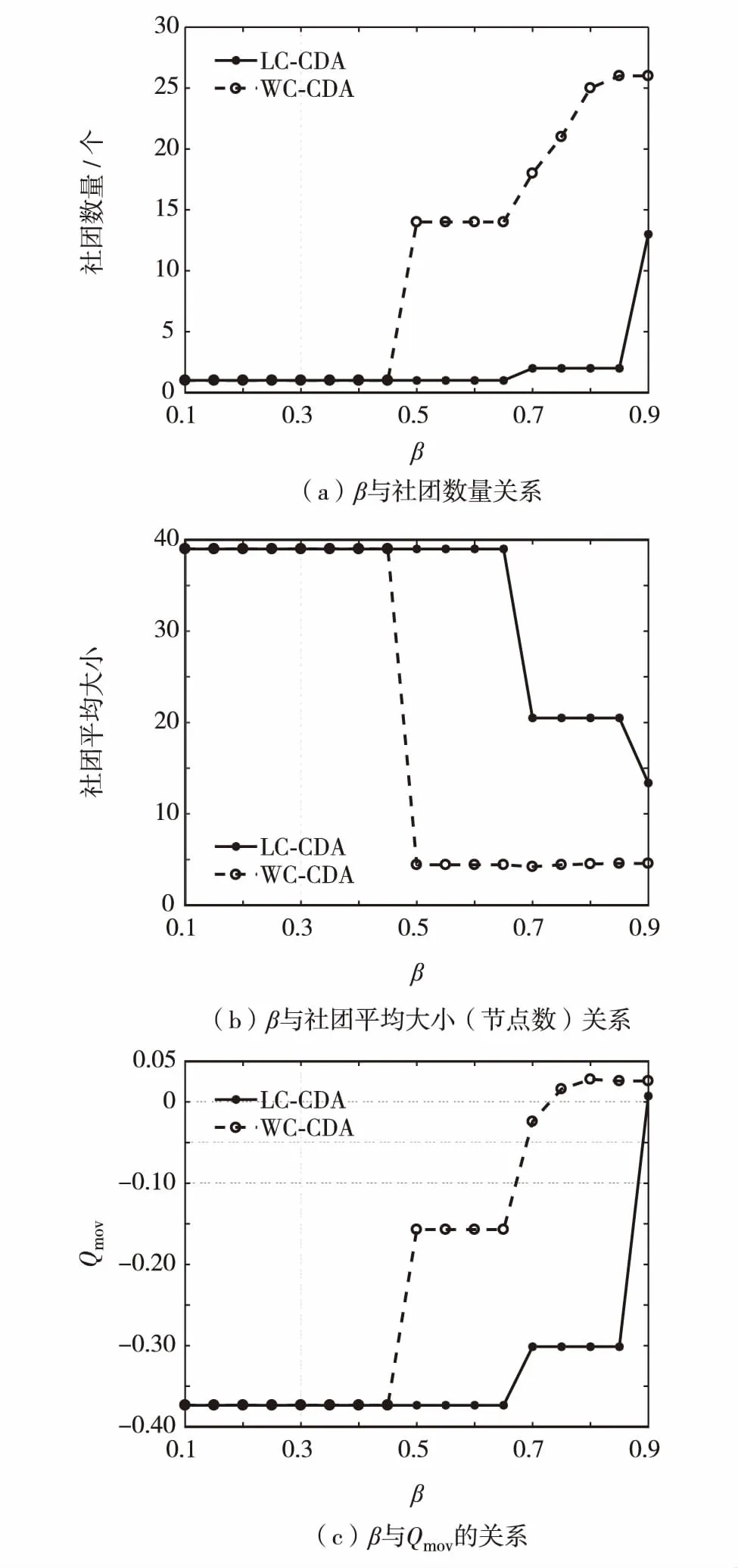
图1 Tailorshop数据集上的仿真结果Fig.1 Result of simulation on Tailsorshop data set

图1是将WC-CDA用于tailorshop数据集时的仿真结果．从图1(a)可见，WC-CDA在0.5≤β≤0.9时可挖掘出更多的社团，而LC-CDA在β≥0.7时仅挖掘出少量社团．由图1(b)可见，WC-CDA所发现的社团尺寸较小．由图1(c)可见，在有社团发现结果的β区间内，WC-CDA算法的Qmov值明显优于LC-CDA算法的Qmov值．

图2 AUCS数据集上的仿真结果Fig.2 Result of simulation on AUCS data set

图2是在丹麦奥胡斯大学计算机科学系(The Department of Computer Science at Aarhus University，AUCS)数据集上的仿真结果．从图2(a)和图2(b)可见，两种算法在不同β值下的社团发现结果与Tailorshop数据集上的仿真结果变化趋势相同．WC-CDA在0.5≤β≤0.9时可检测出更多的社团，而LC-CDA在β≥0.7时检测出少量社团，且WC-CDA所发现的社团平均尺寸较小．由图2(c)可见，WC-CDA的Qmov值高于LC-CDA的Qmov值．

图3是用于FF-TW-YT数据集的仿真结果．从图3(a)可见，WC-CDA在β≥0.5时可检测出大量社团，而LC-CDA所检测的社团数量缓慢增长，且从图1(b)可见，WC-CDA所检测的社团平均尺寸较小．由图3(c)可见，当0.1≤β<0.5时，WC-CDA的Qmov优于LC-CDA；当0.5≤β≤0.9时，LC-CDA的Qmov优于WC-CDA．

图3 FF-TW-YT数据集上的仿真结果Fig.3 Result of simulation on FF-TW-YT data set

结 语

本研究引入弱派系概念使得多层社会网络中的社团划分结果具有更加细粒度的特点．在无向的tailorshop数据集与AUCS数据集网络中，WC-CDA在同一阈值范围内与LC-CDA相比，能挖掘出更多细粒度的社团，可有效发现这种小型网络中的社团．同时，在有向的FF-TW-YT数据集网络中WC-CDA也能挖掘出比LC-CDA更多且规模更小的社团．WC-CDA的提出对于多层社会网络中重叠社团的社团发现具有一定的参考借鉴价值．