余弦定理在n维空间和球面上的推广

赵天宸

(华南师范大学附属中学　510000)

余弦定理是平面几何基本定理之一，早在公元前三世纪，欧几里得在《几何原本》中首先提出了余弦定理的原始形式.经过了长时间的演变，余弦定理如今发展出多种证明方法，为我们提供了多种角度去看待余弦定理，从中诞生出了更多的可能性.本文主要讨论的是余弦定理在高维空间和曲面上的推广.

一、低维余弦定理

基于普遍意义上的二维余弦定理(定理1)：a2+b2-2abcosθ=c2，推广到三维空间(即三维余弦定理)，证明如下：

对于任意三角锥O-ABC，其四个面面积分别为S1,S2,S3,S4，θab指面积分别为Sa与Sb的面的夹角，将OA,OB,OC分别看作向量a,b,c,有

(a-c)×(b-c)=a×b-a×c-c×b.

两边平方，并由向量外积的几何意义得到三维余弦定理(定理2)：

二、高维余弦定理

定义1：

其中，x(a1,a2,a3,…,an)被称为(a1,a2,a3,…,an)的外积,a1=(a11,a12,…,a1n),a2=(a21,a22,…,a2n),…,an=(an1,an2,…,ann),e1=(1,0,0,…,0),e2=(0,1,0,…,0),…,en=(0,0,…,0,1).

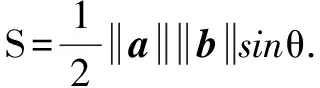
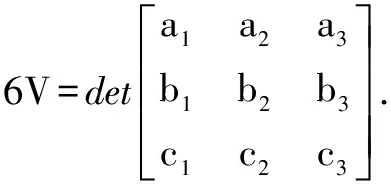
由以上定理和证明发现，二阶行列式表示面积，三阶行列式表示体积，将这个概念推广到高维，有

其中，n∈Z*.特殊地，当n=2时，M表现为面积；当n=3时，M表现为体积.

定理4：定义1中的运算满足分配律，即

x(a1,a2,a3,…,am+am′,…,an)=x(a1,a2,a3,…,am,…,an)+x(a1,a2,a3,…,am′,…,an).(2)

证根据外积的定义，这个定理与以下等式等价.

如果有

那么

证毕.

定理5：(余弦定理)一个n+1维体有n+2个n维物体构成，这些n维物体测度分别记为M1,M2,…,Mn+2.

证有一组向量a1,a2,a3,…,an+1，则x(a1-an+1,a2-an+1,a3-an+1,…,an-an+1)=x(a1,a2,a3,…,an)+x(a1,a2,…,an-1,-an+1)+x(a1,a2,…,an-2,-an+1,an)+…+x(-an+1,a2,a3,…,an,).

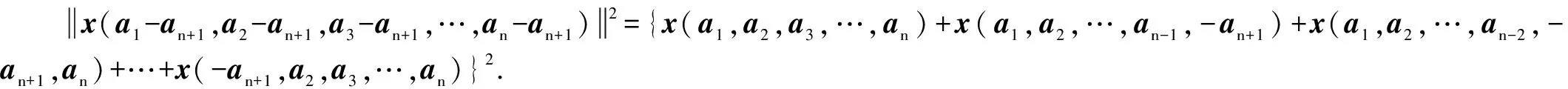
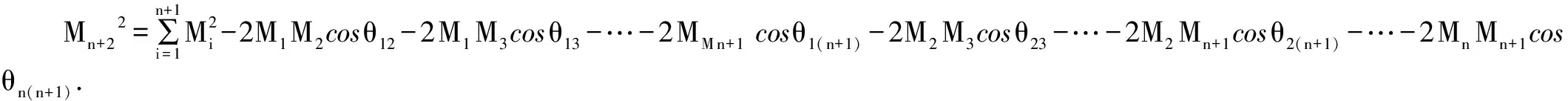
3.球面余弦定理

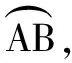
根据以上定义，可以得出：S=θR(其中，S为点A和点B在球面上的距离，θ为OA和OB的夹角，R为球面半径).

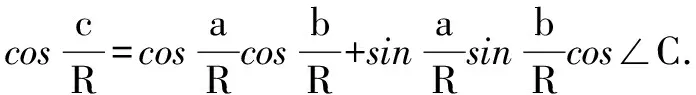
证w，v，u是分别和OA，OB，OC方向相同的单位向量，为了表示∠C，我们需要求出a和b在c点的切线方向.设单位向量n1，n2分别是这两个方向上的单位向量，不难求出

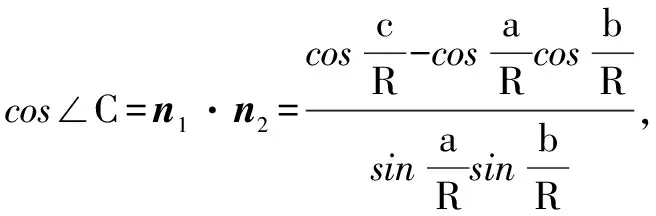
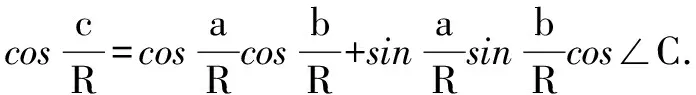
4.高维球面余弦定理

如果令R趋近于无穷大

运用洛必达法则，可以得出

观察该式，不难发现这就是二维平面的余弦定理.这说明平面是半径趋近于无穷大的球面,平面余弦定理其实是球面余弦定理的特殊情况.类似地，n维空间的余弦定理也应该是n维球面余弦定理的特殊情况.

余弦定理对于空间的维度和曲率有着特殊的意义，因而它可以被推广到任意维度包括分数维以及任意曲面上，结合这两种理论，甚至可以推导出任意维度，任意曲率的空间中的余弦定理.这个古老的定理正在孕育着新的可能性.