例谈解析几何问题中的条件转化

石　磊

(江苏省南京市第三高级中学　210000)

一、几何的手段

解析几何问题的两种处理方式——几何化和代数化，教师要引导学生第一时间从系统的高度进行认知，更可以从考试命题的角度这样思考：小题势必不会用大量的运算进行区分考查，即代数化手段不会是解决小题的第一手段，应该从几何化的角度思考为主；解答题恰恰相反，代数化是考查的主要手段，因为用代数的方式解决几何问题才是本章的初衷．

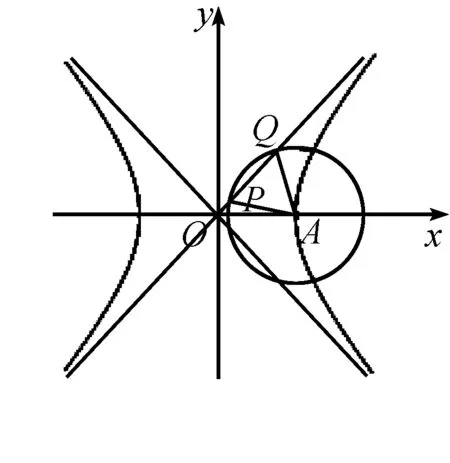
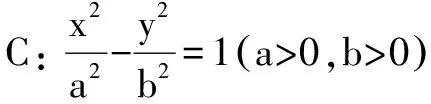
说明离心率问题是典型的解析几何考查小题，其主要解决手段可以分为三个层次：第一是定义的考查，属于简单层面；第二是几何性质的运用，属于中档层次，如何利用几何性质是关键；第三是坐标运算，当前两者都失效的时候，唯有代数化才是正确解决的方式，但是这种方式在小题处理中较少运用．本题是典型的离心率小题，考虑到不涉及双曲线上的点，因此定义基本失效，考虑到渐近线和圆的特殊位置关系，因此几何化手段是主要方式．

二、性质的运用

解析几何问题做多了，学生往往对直线和圆锥曲线联立使用韦达定理有了较多心得，但是在联立之前如何获得有价值的条件转换，却是学生往往缺失的．此时我们应该关注什么？笔者认为，最本质的圆锥曲线性质才是教师要引导学生关注的．看一个问题：

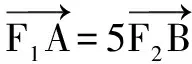
说明此处借助椭圆自身对称性，将原来思考的多个方程只需三个即可，韦达定理的使用也是水到渠成，思路瞬间获得打开，成为了典型的不可多得课堂教学典型问题．

三、角度的处理

解析几何问题离不开角度的考查，直线和圆锥曲线位置关系中典型的角度问题处理是重要问题模型，如何处理角度是一大主要方向．一般来说，角度在解析几何中的处理大都与直线的斜率有关，将角度条件转化为斜率问题，是主要手段．

(1)求椭圆C的方程；

(2)已知A,B为椭圆长轴的两个端点，作不平行于坐标轴且不经过右焦点F的割线PQ，若满足∠AFP=∠BFQ，求证：割线PQ恒经过一定点．

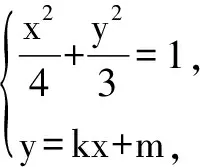
总之，解析几何问题难在条件转化、难在运算、难在综合性要求较高，因此多加以思想上的引导、战术上的指导、实际运算中的操作，便能从实践的角度获得更多的思考、经验的积累，有助于解析几何章节的学习．