有效解决不规则多面体外接球问题的策略

周迎富

(福建省晋江市子江中学　362261)

一、直三棱柱及其补形体

直三棱柱外接球的球心在上下底面外心连线的中点处；常考查三类问题：底面分别是锐角、直角、钝角三角形.直三棱锥可补形成直三棱柱，其外接球球心与对应的直三棱柱相同.

例1(2009全国Ⅰ卷理科) 已知直三棱柱ABC-A1B1C1的各顶点都在同一球面上，若AB=AC=AA1=2，∠BAC=120°，则此球的表面积等于____.

题源变式可变为直三棱锥A1-ABC，侧棱AA1⊥底面ABC，∠CAB=60°或90°或120°，求外接球表面积；

二、直四棱柱及其补形体

在实际解题中，通常还考查正方体、长方体及其补形体的外接球问题，常见的有四类几何体可通过补形成正方体、长方体，来便捷地确定它们的球心和半径.

第①类直角四面体(三条侧棱或三个侧面两两垂直)、直角三棱柱；

第②类四个面都是直角三角形的四面体；

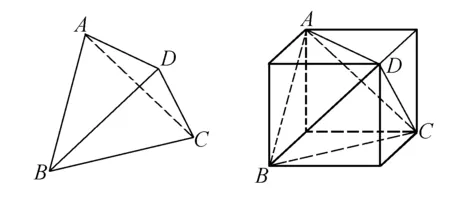
第③类等腰四面体(三组对棱分别相等，AB=CD=a，AC=BD=b，AD=BC=c).

设补形后的长方体长宽高分别为x,y,z，则：

x2+y2=a2，z2+y2=b2，x2+z2=c2

第④类正四面体(各面都是正三角形，设棱长为a)

三、特殊组合型斜三棱锥

在命题中，还有一类考查对象是由等边、等腰、直角三角形构成特殊二面角组合的斜三棱锥，这类斜三棱锥外接球问题的解决步骤是：①通过计算确定三棱锥各个面的特征；②确定特殊三角形的外心；③分别过两个特殊三角形的外心作所在平面的垂线，即得直径所在直线，两直径交点即为球心.

1.直角三角形组合成的三棱锥

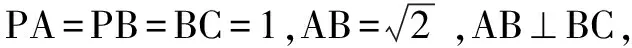
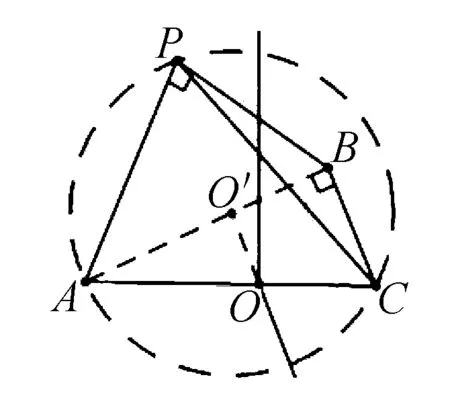
解析法一过Rt△PAB，Rt△ABC的外心分别作垂线，交于点O，点O即球心，AC即直径，故答案：3π.

法三通过验证，易得该三棱锥是以AP或BC为高的直三棱锥，可补形成对应的直三棱柱来求解.

法四通过计算，存在共斜边的两个直角三角形△PAC、△BAC，则斜边AC即外接球直径.

2.等边+直角三角形组合成特殊二面角的三棱锥

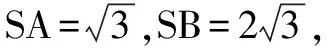
3.等腰+直角三角形组合成特殊二面角的三棱锥

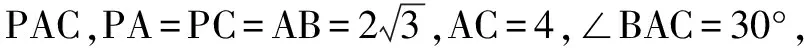
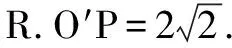
定理得：

外接球的表面积S=18π.

四、其他不规则三棱锥的外接球问题

对于没有存在特殊三角形组合的情况，先确定球心，后利用球心到顶点的距离等于半径、或球心与某个面外心的连线垂直于该面等性质求解.

例5(2017福建质检理数)空间四边形ABCD的四个顶点都在同一个球面上，E,F分别是AB，CD的中点，且EF⊥AB，EF⊥CD，若AB=8，CD=EF=4，则该球的半径等于____.

综上几种类型，解决与球的外接问题重点是确定球心位置和半径，关键是抓住球心到多面体顶点的距离等于半径.掌握好基本的作图能力和平面几何基本知识，发挥好空间想象力，借助于数形结合进行转化,那么问题即可得解.