一种地外天体路标图像的稀疏化表征方法*

胡荣海，黄翔宇,2

0　引　言

从地外天体表面地形信息的表征方法研究现状来看，国内外相关研究大都从测绘的角度，利用轨道器传回的天体表面影像、高程等数据，采用一系列的地形测绘数据处理技术和手段，构建天体表面三维地形模型.对于地外天体着陆探测任务，着陆过程的航程非常远，导致需要的天体表面区域三维地形数据量过于庞大，而星载计算机的存储、计算能力有限，直接利用这些三维地形库进行在轨自主导航是不可行的.为了减少三维地形数据库的大小、降低计算量，提取地形数据库当中一些特征点作为导航陆标是可行的方案，要求这些特征点的相关信息不受光照、旋转和尺度变化等因素的影响.

针对以上问题，国内外专家学者针对图像特征的抽取和表征提出了大量方法.兴趣点的检测包括Harris算法[1]、DoG算子[2]、Fast Hessian算法[3]以及FAST算法[4]等；其中Harris算法的鲁棒性较强，计算量较小，且具有旋转不变性；FAST算子计算量最小，也具有旋转不变性，但鲁棒性不及Harris算子.特征的描述包括SIFT算法[2]、SURF算法[3]、BRIEF描述子[5]、ORB描述子[6]、BRISK描述子[7]以及FREAK描述子[8]等；SIFT特征描述子由于具有极好的稳定性，一直以来都可以说是检验其他算法的一种标准，然而其算法复杂，生成的特征信息量大，对于目前的星载计算机速度，不适合做实时处理；而SURF算法是SIFT算法的一种改进，其性能与SIFT算法相当，同时增强了实时性并降低了描述子的大小，但依然有很大的改进空间.为了进一步降低特征描述子的存储大小，提高匹配速度，有学者提出了BRIEF、ORB、BRISK、FREAK等二进制描述子，极大地减少了描述特征点所需的存储空间和匹配时间.

针对以上问题和研究现状，本文利用着陆器的高度信息，对下降图像进行尺度估计和尺度变换，利用Harris算法提取地图数据中的特征点作为导航路标；从采样模式、主方向计算和描述子位选取策略3个方面对FREAK算法进行了改进；针对图像旋转、尺度变化、图像噪声和尺度估计误差等外界干扰，仿真对比了改进算法与原FREAK算法和SURF算法的匹配性能.

1　基于尺度估计的Harris特征提取

1.1　Harris特征提取

Harris算子是一种基于图像梯度的点特征提取算子，其原理为：如果图像当中某一点向任意方向产生微小偏移都会引起灰度的很大变化，就说明该点是角点.Harris角点响应函数[9]为：

R=det(M)-k·tr2(M)

(1)

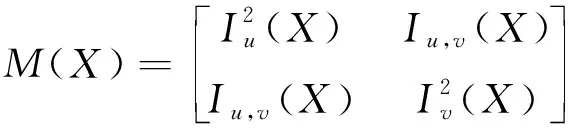
(2)

Iu(X)，Iv(X)和Iu,v(X)分别为图像点X的灰度在u和v方向的偏导以及二阶混合偏导；k为经验因子，通常取0.04～0.06.当某点的Harris角点响应值R大于设定阈值T时，表明该点为角点.

1.2　图像尺度估计与尺度变换

由于Harris角点不具备尺度不变性，当下降图像与轨道图像存在较大尺度差异时，会降低特征点的重复检测性.引入图像尺度金字塔可以有效解决该问题，但同时也增加了计算量；针对地外天体着陆器，可以利用测距信息对下降图像进行尺度估计与尺度变换来减小尺度的影响.

首先，利用导航滤波器可以得到较精确的高度信息h,并已知地图数据库的分辨率RO、导航相机的视场角大小αfov和下降图像的像素大小[m,m],可以估计下降图像I的分辨率RL和尺度因子ks:

(3)

ks=RL/RO

(4)

利用高斯核G模糊处理下降图像I:

L(x,y)=G(x,y,σ)*I(x,y)

(5)

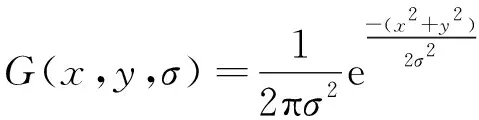
(6)

其中，L(x,y)为高斯模糊后的图像，G(x,y,σ)为高斯核，*为卷积运算.

对L进行ks倍降采样，利用Harris算法提取图像中的特征点.

2　FREAK描述子分析与改进

2.1　FREAK描述子简介

FREAK描述子模拟了人类视网膜对图像信息进行提取的过程.人类视网膜上包含Fovea区域、Para区域和Peri区域[8]，分别用于提取图像特征的细节信息和轮廓信息.FREAK描述子就是借鉴了人类视觉分区域获取信息的结构而提出的算法，通过对特征点周边进行采样，利用采样点之间的灰度关系构建二进制描述子.

FREAK描述子的采样点分布情况与人类视网膜感受域相似，如图1所示，采样模型的中央为待描述的特征点，在特征点的周围均匀、对称地选取了42个采样点，一共7层，每层6个.每个采样点都要经过高斯平滑进行模糊，采样点所在圆域的半径代表高斯核的半径，半径越大表示信息越模糊.

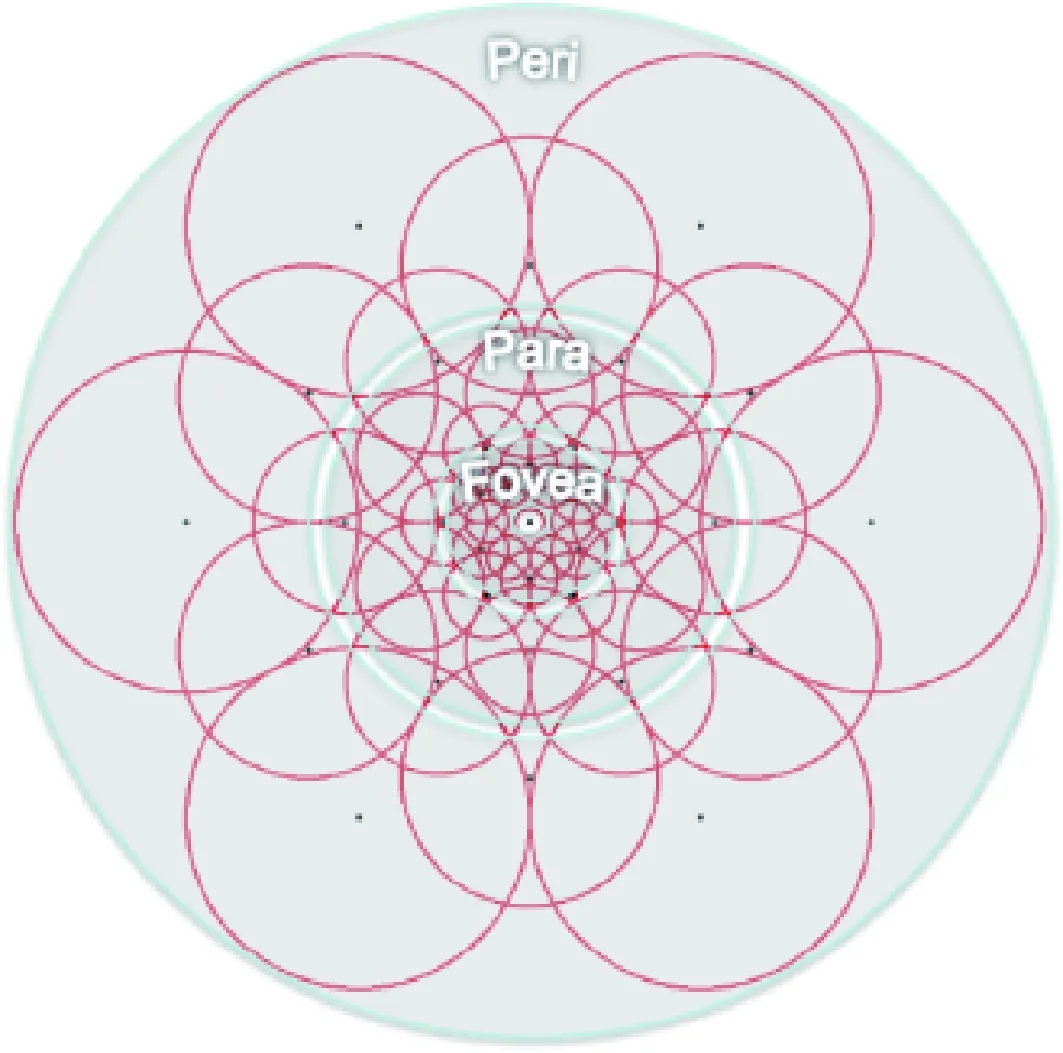
图1　FREAK算法的采样模式Fig.1　Sampling mode of FREAK algorithm

(7)

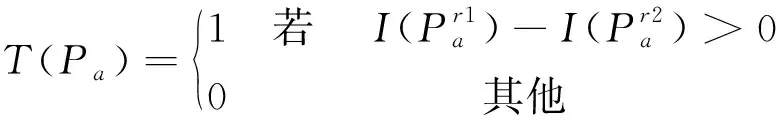
(8)

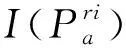
为了得到信息含量最多的描述位，利用以下步骤剔除903位描述子中的信息冗余位：

1) 对50 000个特征点进行特征描述，利用这些描述子组建一个50 000×903的矩阵D.

2) 计算D中每一列的均值.均值越接近0.5说明该列方差越大，信息含量也越多.

3) 按照方差从大到小的顺序对D矩阵的每一列进行重新排序.

4) 保留方差最大的一列，选择与该列协方差最小的列加入到新组成的描述向量中.

由以上4个过程选取了其中信息含量最多的512位作为特征描述子，一个描述子占用64个字节.

为了估计特征的旋转角度，在特征点周围选取一定数量的点对，利用这些点对的局部灰度信息计算特征主方向.一共选取了45个采样点对，如图2所示.

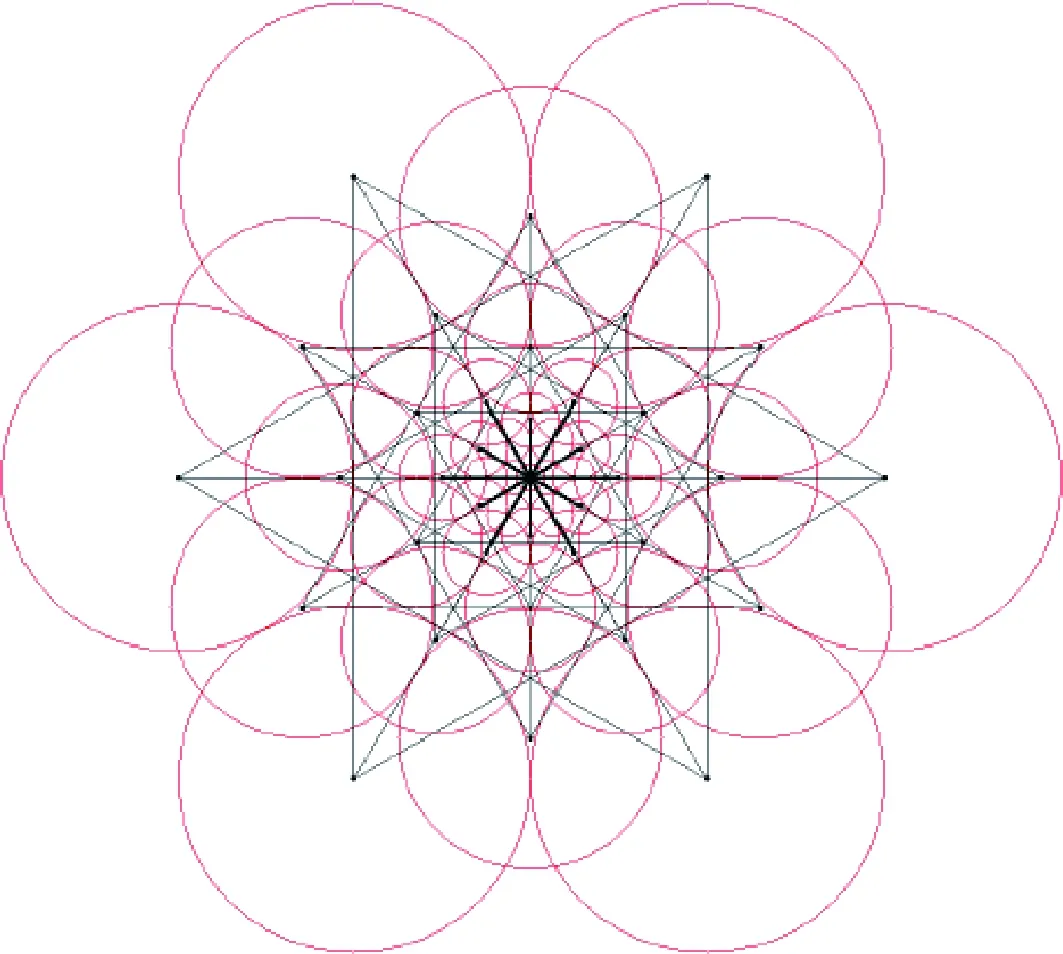
图2　计算主方向的采样点对Fig.2　Point pairs for computing the main direction

(9)

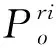
2.2　FREAK描述子分析与改进

当存在外界环境干扰的情况下，FREAK算法表现出以下问题：

(1) 在图像发生连续旋转时，FREAK算法的正确匹配对数随旋转角周期性变化，且波动较大.

由于FREAK算法的采样模式是每层选取6个采样点，最多只能利用特征点周围12个方向上的梯度信息，存在较多方向信息的缺失；同时用于计算主方向的点对选择也不尽合理，利用了较多内部的细节信息，而细节信息非常容易受到外界环境的干扰，使主方向计算误差较大，导致特征描述子信息错位，所以特征正确匹配率对图像旋转变化比较敏感.

(2) 当图像尺度变化较大或者存在图像噪声时，FREAK算法出现较多误匹配.

因为其512维描述子的选取与排列方式不合理，同样利用了较多容易受到外界干扰的图像细节信息来对特征进行表征，并且没有严格按照信息从粗到精的顺序进行排列，对特征的描述能力不足，导致较多误匹配或匹配失败.

针对以上问题，从采样模式、主方向计算和描述子位选取策略对原FREAK算法进行了改进.

1) 采样模式的改进

增加每层采样点的数目能够获取更多方向的梯度信息，从而降低图像旋转对特征匹配的影响；但采样点越多，算法越复杂，计算量也越大.对于人类而言，只需要利用较为模糊的外围轮廓信息就可以识别一个物体，而内部细节信息在识别中占次要位置；同时由采样模式决定的外围采样点信息是经过较大σ值的高斯函数进行模糊处理得到的，具有很强的抗干扰能力，而内部采样点信息是经过较小σ值的高斯函数进行模糊处理得到的，更容易受到外界干扰，是不稳定的.综合考虑以上因素，适当增加外围稳定的模糊信息，减少内部不稳定的细节信息，每层选取8个采样点，一共5层， 41个采样点，可以提供16个方向上的梯度信息，同时减少了总的计算量.采样模式如图3所示.

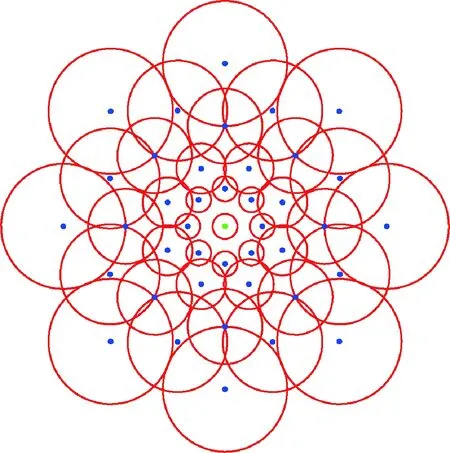
图3　改进的采样模式Fig.3　Improved sampling mode

2) 主方向计算的改进

由于特征主方向的计算直接赋予了特征的旋转不变性，如果主方向存在较大偏差，就会使特征描述子发生位偏移，导致匹配失败或出现较多误匹配.原FREAK算法只利用了45个采样点对的梯度信息，并且包含较多内部不稳定的细节信息，导致主方向计算误差较大.为了提高主方向的准确性，应该尽可能多的利用较为稳定的外围模糊信息，而内部细节信息起修正作用.选取最外部两层之间的40个相互梯度信息和最里部两层之间的16个相互梯度信息，一共选取了56个采样点对，成中心对称，且每个方向所包含的信息总量相同，采样点对结构如图4所示.

图4　改进的用于主方向计算的采样点对Fig.4　Improved sampling mode for main direction calculation

3) 描述子位选取策略的改进

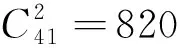
图5　0.5与每一列的均值之差Fig.5　The difference between 0.5 and the mean value of each column

可以验证的是，利用以上采样模型得到的任何图像特征描述子位统计信息都与上图相似.越接近于0表示该列的方差越大，表明任意特征的该描述子位更近似服从于随机分布，所包含的信息量也越多.图中共有5个波峰，从左至右分别为每层采样点与内部采样点之间的相互梯度关系，表征了信息从模糊到精细的划分；为了使特征匹配过程更加高效和可靠，应首先匹配模糊信息进行粗筛选，当模糊信息达到较高相似度后再匹配细节信息以确定最相似的特征；按照信息匹配从粗到精的原则，依次从五层采样点对所生成的描述子位当中提取与0最接近的位组成特征描述子，一共选取了256个二进制位，共占用32个字节.

经过以上3方面的改进，使计算量比原算法降低了30%～40%，同时使描述子的大小降低为原算法的一半，既减少了匹配过程的计算量，又降低了对存储空间的需求.

3　仿真结果与分析

为了检验改进算法的特征匹配性能，针对图像旋转变化、图像尺度变化、图像噪声和尺度估计误差等外界干扰，与SURF算法和原FREAK算法进行了比较.SURF算法采用欧氏距离计算特征相似度，改进算法和原FRTEAK算法利用二进制串的汉明距离计算特征相似度；模糊信息相似度阈值设为85%，细节信息相似度阈值设为92%.最后，利用了RANSAC(Random Sample Concensus)方法检验正确匹配对数，特征点位置误差阈值设为0.5个像素距离.仿真结果如下：

由图6可知，当图像发生旋转变化时，3种算法的正确匹配对数都随旋转角度成周期性变化。相对于另外两种算法，改进算法的正确匹配对数具有明显优势，且波动较小，对图像旋转变化具有更好的抗干扰能力。但正确率的标准差稍大，即稳定性比原FREAK算法略低，如表1所示；这是因为改进算法大幅缩减了描述子的位数，可能导致两个不同的特征点由于缺乏可以进行区分的特征位而造成误匹配，但总体影响不大。

图7为尺度变化对匹配性能的影响，当尺度过大造成正确匹配对数接近于0时，不再给出该尺度下的正确率。可以看出，图像尺度过大或过小都会导致正确匹配对数迅速下降，因为尺度变化会大幅降低序列图像间的特征重复率。虽然SURF算法具有尺度不变性，但当尺度大于3后，正确匹配对数几乎为0。而改进的算法由于引入了尺度估计，依然能够正确匹配到较多的特征点，正确率也高于另外两种算法，且稳定性更好，如表2所示。

表1　在图像旋转变化的影响下，正确率的标准差Tab.1　The standard deviation of correctness under the influence of image rotation

表2　在图像尺度变化的影响下，正确率的标准差Tab.2　The standard deviation of correctness under the influence of scale-change

由图8可以看出，3种算法的正确匹配对数都随斑点噪声的增强而降低。当斑点噪声强度较低时，改进算法总体上能够正确匹配更多的特征点。当噪声强度较高时，3种算法的正确匹配对数非常接近；但改进算法的正确率总体较高，波动较小，对图像噪声具有较强的鲁棒性，如表3所示。因为改进算法主要利用了特征点的外围模糊信息来构建描述子，对图像噪声具有更强的抗干扰能力。

表3　在图像噪声的影响下，正确率的标准差Tab.3　The standard deviation of correctness under the influence of image noise

由于改进算法与原FREAK算法都不具备尺度不变性，故在1.2节中对图像进行了尺度估计，当尺度估计存在一定误差的时候，会降低图像匹配的性能。

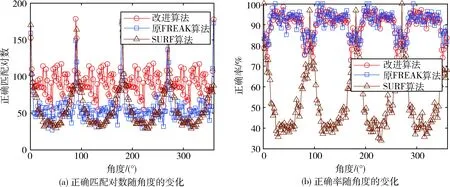
图6　图像旋转对匹配性能的影响Fig.6　Influence of image rotation on matching performance

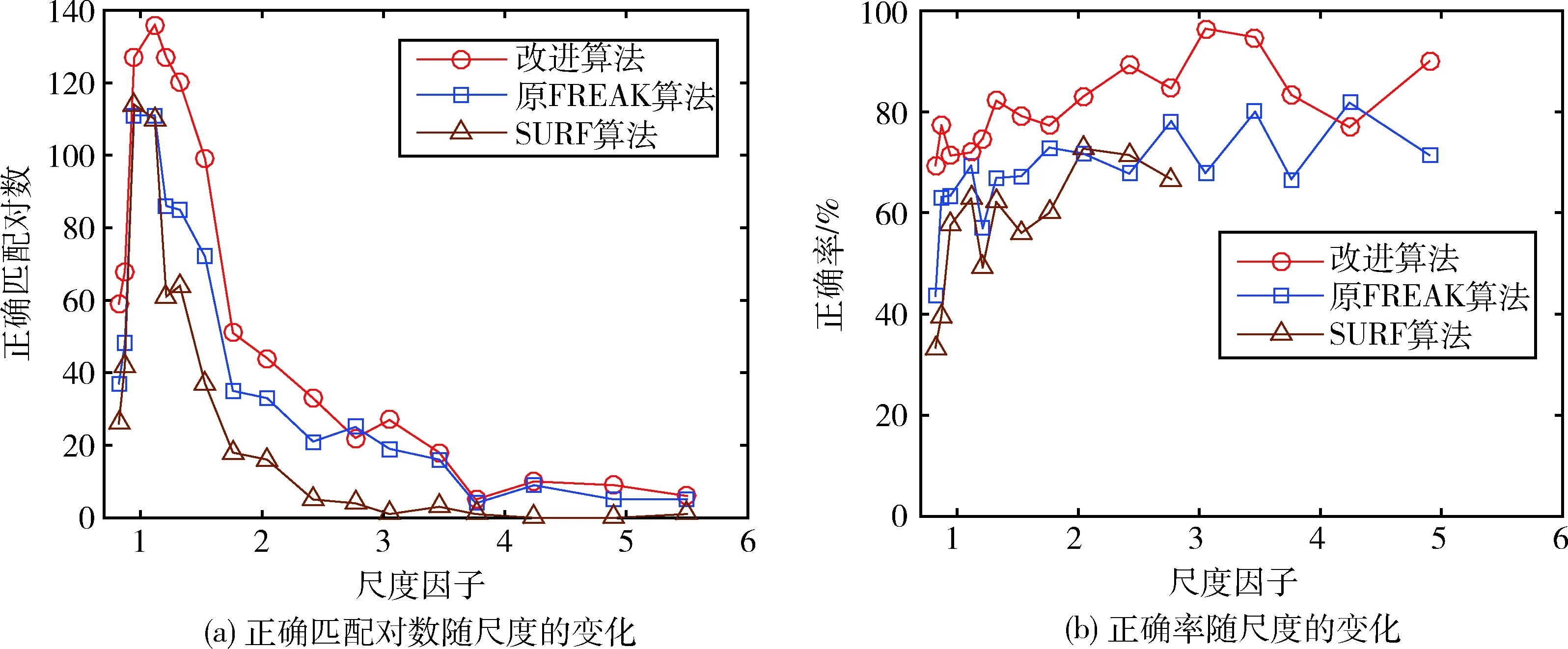
图7　尺度变化对匹配性能的影响Fig.7　Influence of scale change on matching performance

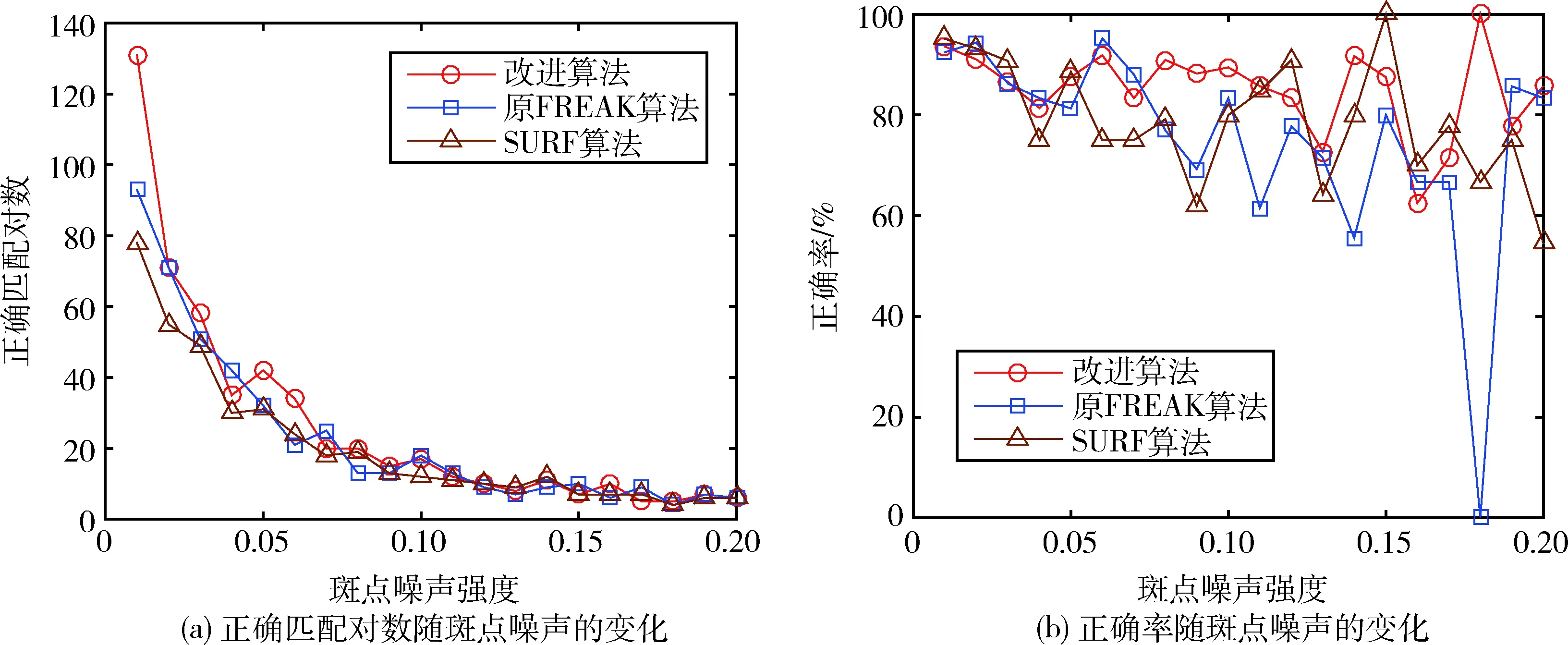
图8　斑点噪声对匹配性能的影响Fig.8　Influence of speckle noise on matching performance

图9模拟了尺度估计误差对匹配性能的影响，由于SURF算法具有尺度不变性，不需要对图像尺度进行估计，这里只对比改进算法与原FREAK算法的匹配结果.可以看出原FREAK算法对尺度估计的精度依赖较高，而改进的算法对尺度估计误差呈现出一定的鲁棒性；在尺度估计值低于准确值的某个范围之内，正确匹配对数几乎不受影响.

由以上4个仿真实验可知，提出的改进算法能够很好地应对图像旋转、尺度变化、图像噪声和尺度估计误差等外界干扰；相对于原FREAK算法和SURF算法能够正确匹配到更多的图像特征，且具有更好的鲁棒性.

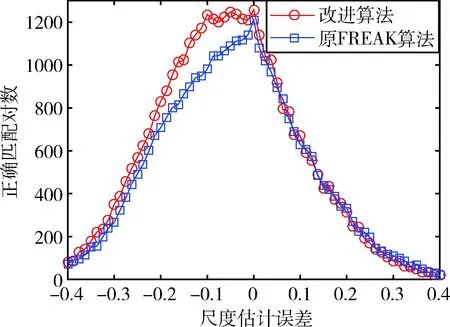
图9　尺度估计误差对匹配性能的影响Fig.9　Influence of scale estimation error on matching performance

4　结　论

针对地外天体着陆任务，由于可以通过导航滤波器获取着陆器的高度信息，提出了基于尺度估计的Harris算法检测路标特征；就特征表征信息量大和计算量大等问题，选择了最具优势的二进制特征描述子.分析了FREAK算子的优势和不足，从采样模式、特征主方向的计算和特征描述二进制位的筛选3个方面对FREAK算法进行了改进.减少了总的计算量，并缩小了描述子的尺寸，每一个路标特征只需要256位二进制串来描述，相比原算法的512位二进制串，进一步降低了匹配时间和对存储空间的要求；同时增强了特征描述性能，使特征正确匹配对数和正确率都得到了相应提升，说明提出的算法更适合地外天体着陆任务应用.