用于三维点云表示的扩展点特征直方图算法*

庄祉昀，张 军，孙广富

(国防科技大学 电子科学与工程学院， 湖南 长沙 410073)

用于三维点云表示的扩展点特征直方图算法*

庄祉昀，张 军，孙广富

(国防科技大学 电子科学与工程学院， 湖南 长沙 410073)

局部特征提取在点云相关应用中具有十分重要的作用，因此提出一种用于点云局部特征表示的扩展点特征直方图描述子。针对邻域点的两两点对提出一系列不变量；在特征点上构建一个局部参考坐标框架以获得特征描述子对旋转和平移的不变性；将关键点局部邻域划分成多个子空间，并依据每个子空间中的点对不变量构建一个直方图；将所有直方图串联起来得到扩展点特征直方图特征描述子。采用Bologna公共数据集对扩展点特征直方图特征描述子的性能进行测试，并与多个现有算法进行对比。结果表明，扩展点特征直方图特征描述子获得了良好的性能，其结果优于多个现有的特征描述子。

点云；局部特征；特征表示；点集；特征直方图

特征提取是计算机视觉和模式识别领域的一个核心基础问题，目前业界已提出多种点云局部特征描述算法，但如何实现对局部点云的高鉴别力描述依然是一个有待解决的问题。Johnson等[1-2]采用点云的法向量及点的位置信息提出了一个spin image特征。对于特征点的每一个局部邻域点，均可采用两个参数进行表示，其中一个参数是该邻域点到特征点法向量的距离，另一个参数是该邻域点到特征点切平面的距离。接着，对所有邻域点依据这两个参数值进行二维直方图统计以获得spin image特征描述子。Spin image特征描述子具有对刚性变换的良好不变性[1]。Hetzel等采用包括点云深度值、表面法向量以及曲率等在内的多个属性构建局部特征描述子[3]。这些特征描述子实现简单且对视点变化具有良好的不变性。Flint等[4-5]通过对关键点与局部邻域点的法向量夹角进行直方图统计以得到THRIFT特征描述子。Chen等[6]采用局部邻域点的形状指数和法向量变化这两类信息构建LSP(local surface patch)特征描述子。Rusu等[7]通过计算关键点及其邻域点的多个几何属性关系构建直方图，并将多个直方图串联起来得到快速点特征直方图(Fast Point Feature Histograms， FPFH)特征描述子。Pang等[8]通过体素化计算一系列3D Harr特征描述子，并将这些特征描述子用于包含遮挡的点云下的目标识别。Tombari等[9-10]在构建局部参考坐标框架的基础上提出了一种方位直方图(Signature of Histograms of OrienTations， SHOT)特征描述子。实验结果表明，SHOT特征描述子在鉴别力和稳健性之间获得了良好的折中。Cirujeda等[11]对三维局部表面的形状与颜色信息进行融合以获得MCOV特征描述子。MCOV特征对刚性变换具有不变性，且对噪声和数据分辨率变化具有稳健性。Hariri等[12]亦提出了一种基于协方差的局部特征描述子。此外，近期还有全局正交物体描述子(Global Orthographic Object Descriptor, GOOD)[13]、距离直方图描述子[14]、二值形状模式描述子[15]以及快速稳健局部特征描述子[16]等一系列算法被提出。

1 对几何属性不变量

大多数的现有特征描述算法直接采用邻域点的几何属性(如法向量、曲率[17]及积分体积[18]等)或空间坐标构建点云局部特征描述子。由于只采用了邻域点上的几何属性或空间坐标来对关键点邻域进行表示，这类特征描述子缺乏上下文结构信息，因此，点云中的许多关键点将得到非常相似的特征描述子，从而在特征匹配时带来大量的错误特征匹配。若能将邻域点的上下文信息添加到特征描述子中，则提取到的特征描述子将具有更高的鉴别力和更多的信息量。一种直观的思路是将点对的信息用于特征描述，从而使获得的特征描述子包含上下文信息。受此启发，基于点对属性不变量，提出了扩展点特征直方图(Extended Point Feature Histograms, EPFH)特征描述子。

1.1 Darboux框架

为获得关键点邻域表面的点对几何属性，首先为每一个点对构建一个Darboux框架。给定一个关键点pk及其法向量nk，邻域点pi及其法向量ni，则Darboux框架的三个坐标轴(u,v,w) 可通过这两个点及它们的法向量构建得到，即：

u=nk

(1)

v=(pi-pk)×nk

(2)

w=u×v

(3)

图1 Darboux框架示意图Fig.1 Illustration of the Darboux frame

关键点pk定义为该Darboux框架的原点，其示意图如图1所示。可以看出，Darboux框架给出了描述两个点之间关系的一种方式。后文将基于Darboux框架定义一系列点对几何属性不变量用于特征描述。

1.2 点对几何属性不变量

当得到一个关键点pk及其邻域点pi的Darboux框架后，可据此计算多个成对几何属性不变量[7]。第一个不变量定义为向量v和向量ni的点积，即：

α=vni

(4)

第二个不变量为向量u与连接点pk和点pi的直线之间的点积，即：

(5)

第三个不变量定义为：

θ=arctan(wni,uni)

(6)

这些不变量反映了关键点pk及其邻域点pi之间的几何关系。然而，这些不变量只给出了关键点与邻域点之间的几何关系，而没有反映出空间信息，因此提出一种同时包含几何关系和空间关系的EPFH特征，从而使得特征描述子的鉴别力更强。

2 EPFH特征提取

现有的点特征直方图(Point Feature Histograms, PFH)特征描述子将关键点邻域的所有点对几何属性累加以得到特征描述子[19]；现有的FPFH特征描述子只将关键点与邻域点的点对属性不变量累加到一个直方图中[7]。这两种特征描述子均缺乏点云空间分布的信息，本文提出的EPFH特征将同时包含几何信息和空间分布信息。EPFH特征的生成过程主要包括如下步骤：局部参考坐标框架构建、直方图生成以及直方图压缩。

2.1 局部参考坐标框架构建

一个良好的特征描述子应该对刚性变换(包含旋转和平移)具有不变性，以实现不同视角下的两个点云之间的精确特征匹配。一个典型思路是给每个关键点赋予一个局部参考坐标框架，并在该参考坐标框架下构建特征描述子[10，20]。

给定一个关键点pk及其邻域点集合{pi|i=1,2,…,N}，计算其邻域点的加权协方差矩阵如下：

(7)

式中，r为支撑域的大小，di为关键点pk到其邻域点pi的距离。

对协方差矩阵M进行特征值分解，得到：

M=VDVT

(8)

式中，D为协方差矩阵M的特征值构成的对角矩阵，V为协方差矩阵M的特征向量{e1,e2,e3}构成的矩阵。

由于特征向量相互正交，因此可采用协方差矩阵M的三个特征向量来构建局部参考坐标框架。为得到一个唯一的局部参考坐标框架，需要消除每个特征向量的方向模糊性。本文采用文献[10]的方法来消除特征向量的方向模糊，该方法首先计算从关键点到所有邻域点的向量，然后统计这些向量的分布情况，并使特征向量方向与前述向量的多数方向相一致。

具体而言，首先选出与向量e1方向一致的所有邻域点，即：

(9)

然后选出与向量e1方向相反的所有邻域点，即：

(10)

利用类似方法作用于向量e3以获得参考坐标框架的z轴。当得到x轴和z轴后，y轴定义为z×x。因此，最终的局部参考坐标框架将以关键点pk作为其原点，以x轴、y轴和z轴作为其坐标轴。

2.2 直方图生成

为生成特征描述子，首先将关键点的所有邻域点均变换到该关键点的局部参考坐标框架下，从而使得后续得到的直方图具有对刚性变换的不变性。接着，采用一个三维球形栅格沿距离、方位角和俯仰角三个维度将关键点的邻域空间划分成多个子空间。图2给出了该三维球形栅格的示意图。该栅格将空间在距离维度上划分成2部分，在方位角维度上划分成8部分，在俯仰角维度上划分成2部分。因此，关键点邻域空间共被划分成32个子空间。

关键点的邻域空间只被划分成了32个子空间，该划分总体上来说是较粗糙的。这样设计的目的在于：由于每个子空间中采用了点对几何属性不变量进行特征描述，因此本身已具有较高的鉴别力，只需要划分少量的子空间即可实现高鉴别力地特征描述；较小的子空间数量有利于获得紧凑且高效的特征描述子。一个紧凑的特征描述子是高效特征匹配和目标识别等高层视觉任务的基础，是提高运算效率的关键。

图2 三维栅格示意图Fig.2 Illustration of the 3D grid

在每个子空间中，分别采用点对几何属性不变量α，φ和θ各构建一个局部直方图，然后将这些直方图连接起来得到该子空间中的子特征。最后将各个子空间中的子特征连接起来得到最终的特征描述子。通过实验发现，直方图的维度设置为10时可以很好地获得特征描述子长度与鉴别力之间的折中。因此，本文设置每个直方图维度为10，则最终的特征描述子长度为10×3×32=960。由于采用了不同的不变量来描述点云所代表的局部表面，因此得到的特征描述子具有很强的鉴别力。

2.3 直方图压缩

由于特征描述子长度为960，其维度太高，依然难以实现高效的特征存储与匹配。事实上，特征描述子中依然存在较多的冗余信息，因此可以采用主成分分析(Principal Component Analysis, PCA)法获得更加紧凑且鉴别力更强的特征描述子。PCA作为一种典型的降维方法，在特征压缩、特征选择以及目标识别等领域得到了大量的应用[21]。PCA通过将高维特征描述子映射到低维向量空间以揭示特征描述子的内在结构。也就是说，通过PCA可用一个低维特征描述向量来表示高维特征向量中的大部分信息。

给定一个用于训练的特征描述子集合{fi|i=1,2,…,Nf}，首先计算其协方差矩阵：

(11)

对协方差矩阵C进行特征值分解，即得到：

C=VDVT

(12)

式中，D是协方差矩阵C的特征值构成的对角矩阵，V由协方差矩阵C的特征向量构成。

为降低特征描述子的维度，对C的特征向量依据其对应的特征值从大到小进行排序，并选择前Nfd 2个特征向量构成PCA投影矩阵Vc。特征向量个数的选择需满足如下要求：

(13)

式中，{λi|i=1,2,…,Nfd 1}为依降序排列的特征值，Nfd 1为原始直方图的维度，Nfd 2为投影后的特征描述子维度，η为特征压缩的系数。

因此，压缩后的特征描述子定义为：

(14)

3 实验结果

本节将在Bologna数据集上测试所提的EPFH特征描述算法，并将其与多个现有算法进行对比，包括spin image[2]，LSP[6]和THRIFT[5]。与文献[9]一致，本节将每个场景的特征描述子与模型库中的特征描述子进行匹配，从而测试特征描述子的匹配性能。

3.1 实验设置

给定一个包含遮挡和背景干扰的场景以及一组模型，特征匹配的任务在于获得场景局部特征描述子与模型局部特征描述子之间的特征对应关系。采用召回率-精度曲线这一常用指标来度量特征描述子的性能。首先，从每个模型上随机提取1000个特征点，然后采用已知的变换关系获得这些特征点在场景中的真实对应点。在测试时，计算每个场景特征描述子与所有的模型特征描述子的距离以获得最近和次近的模型特征描述子，进而将最近距离除以次近距离得到距离比值。若该距离比值小于一个预先设定的门限τf，则认为该场景特征描述子与最近模型特征描述子之间构成一个特征对应关系。采用场景与模型之间的真实变换关系可以确定一个特征对应关系是否正确。具体而言，可采用真实变换关系将场景与模型变换到同一个坐标系下，然后计算特征对应关系中的两个特征点之间的距离，若该距离较小，则认为获得的特征对应关系是正确的，否则认为是错误的。因此，特征匹配的精度定义为正确特征对应数量与所获得的所有特征对应数量的比值，而特征匹配的召回率定义为正确特征对应数量与所有真实特征对应数量的比值。实际上，特征匹配的精度与召回率依赖于门限τf的选取。采用多个不同的门限便可得到不同门限下对应的一系列召回率和精度，即获得召回率-精度曲线。需要说明的是，文中对所有特征描述子的测试均采用相同的特征点，因此对不同特征描述子的比较结果是客观公正的。此外，本文采用随机选取而非某个特定特征检测算法，因此可以避免特征检测算法本身对特征描述子性能带来的影响。

本文采用公共的Bologna数据集进行实验。该数据集包含了斯坦福3D扫描数据集中的6个模型，以及通过对多个模型进行随机旋转和平移得到的45个场景。因此，数据集中的场景包含了复杂的形状、丰富的几何细节、较强的背景干扰以及不同的姿态变化，这些问题增加了算法的挑战性。每个场景与模型之间的真实刚性变换关系在数据集获取的过程中便已记录下来。

3.2 噪声下的性能

本小节将测试不同强度噪声下的EPFH特征性能。实验中，将标准差分别为0.1 mr，0.2 mr，0.3 mr和0.4 mr的高斯噪声加入到每个场景中。不同高斯噪声下的召回率-精度曲线如图3所示。

可以看出，所提的EPFH特征描述子在不同强度的高斯噪声下均取得了最好的性能：

1)对于加入0.1 mr标准差噪声的场景，所提的EPFH特征描述子在精度为90%时取得的召回率可达到90%左右，大大超越了spin image特征描述子(spin image特征描述子在精度为90%时的召回率只有44%)。

2)当噪声标准差从0.1 mr增加到0.4 mr时，EPFH特征描述子的优势更加明显。当噪声标准差为0.4 mr时，EPFH获得的最高召回率为51.31%，而spin image，LSP和THRIFT特征描述子获得的最高召回率分别仅为6.86%, 2.62%，1.58%。

3)总体而言，当噪声增加时，EPFH特征描述子的性能逐步下降。这是由于，噪声增加会导致点云中点位置和法向量均与原始的无噪声点云上的值相差较大，使得得到的Darboux框架和点对属性不变量均发生较大变化，因此特征描述子也与无噪声点云上的特征描述子相差较大。

4)EPFH特征描述子对噪声相对比较稳健。当噪声标准差为0.1 mr时，获得的最大召回率为90%，而当噪声标准差上升到0.2 mr时，获得的最大召回率依然高达80%。特别地，当噪声标准差增加到0.4 mr时，获得的最大召回率依然可达50%以上。EPFH在噪声标准差为0.4 mr时的性能甚至与spin image在噪声标准差为0.1 mr时的性能相当，这充分表明了本文算法在含噪声场景下的优势。

(a) 高斯噪声标准差0.1 mr(a) Gaussian noise standard deviation of 0.1 mr

(b) 高斯噪声标准差0.2 mr(b) Gaussian noise standard deviation of 0.2 mr

(c) 高斯噪声标准差0.3 mr(c) Gaussian noise standard deviation of 0.3 mr

(d) 高斯噪声标准差0.4 mr(d) Gaussian noise standard deviation of 0.4 mr图3 不同高斯噪声下的特征匹配召回率和精度曲线Fig.3 Precision and recall for feature matching under different Gaussian noise

3.3 数据分辨率变化下的性能

本小节将测试特征描述子在不同数据分辨率下的性能。实验中，将每个场景点云降采样到原分辨率的1/4和1/8，得到不同分辨率下的召回率-精度曲线如图4所示。

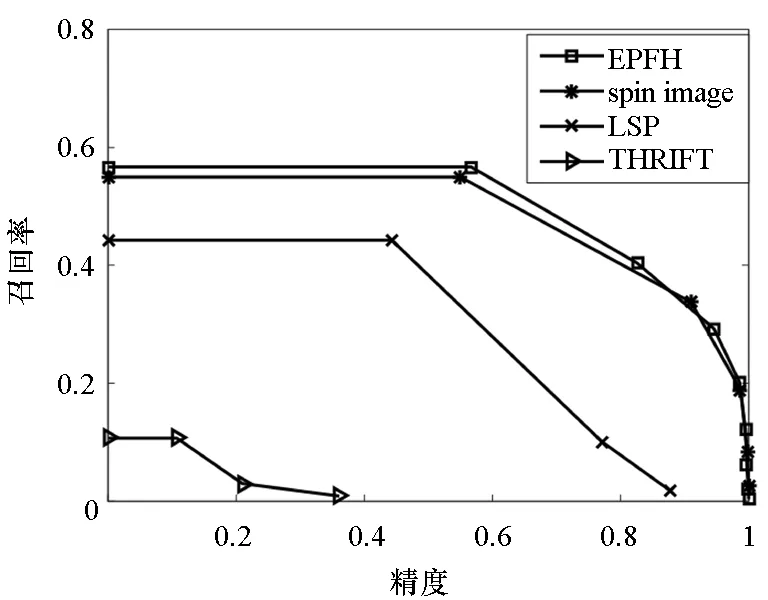
(a) 1/4降采样率 (a) 1/4 down-sampling

(b) 1/8降采样率(b) 1/8 down-sampling图4 不同数据分辨率下的特征匹配召回率和精度曲线Fig.4 Precision and recall for feature matching under different point cloud resolutions

由图可以看出，所提的EPFH特征描述子在两个不同的数据分辨率下均获得了比其他算法更好的性能。具体而言，EPFH在1/4降采样时的性能略优于spin image，其获得的最高召回率为56%。LSP和THRIFT的性能差于EPFH和spin image，获得的最高召回率仅分别为44%和11%。当采样率为1/8降时，EPFH的性能大大优于spin image特征。EPFH获得的最高召回率为50%，而spin image获得的最高召回率只有35%左右。由此可知，所提的EPFH特征描述子对数据分辨率变化较为稳健。

此外，所提EFPH算法是在FPFH特征提取算法[7]的基础上改进而得到，在大量数据集上的测试结果表明FPFH具有非常高的计算效率[22]。由于EPFH继承了FPFH高效的特点，因此EPFH算法本身也具有非常高的运算效率。

4 结论

本文提出了一种用于三维点云表示的EPFH特征描述子。该算法首先对一个点对构建Darboux框架并依此获得多个不变属性；接着，在每个关键点上构建一个局部参考坐标框架并将邻域空间划分成多个子空间。通过对不变属性进行直方图统计以获得每个子空间的子特征，最后将所有子特征串联并经过压缩以得到最终的EPFH特征描述子。在Bologna数据集上测试了该特征描述子在不同噪声和数据分辨率下的性能。实验结果表明，所提的EPFH特征描述子不仅鉴别力强，且对噪声和数据分辨率变化稳健，其获得了比spin image，THRIFT和LSP特征更好的性能。

References)

[1] Johnson A E, Hebert M. Surface matching for object recognition in complex three-dimensional scenes[J]. Image and Vision Computing, 1998, 16(9/10): 635-651.

[2] Johnson A E, Hebert M. Using spin images for efficient object recognition in cluttered 3D scenes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21(5): 433-449.

[3] Hetzel G, Leibe B, Levi P, et al. 3D object recognition from range images using local feature histograms[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2001.

[4] Flint A, Dick A, van den Hengel A. Thrift: local 3D structure recognition[C]//Proceedings of the 9th Biennial Conference of the Australian Pattern Recognition Society on Digital Image Computing Techniques and Applications, 2007: 182-188.

[5] Flint A, Dick A,van den Hengel A. Local 3D structure recognition in range images[J]. IET Computer Vision, 2008, 2(4): 208-217.

[6] Chen H, Bhanu B. 3D free-form object recognition in range images using local surface patches[J]. Pattern Recognition Letters, 2007, 28(10): 1252-1262.

[7] Rusu R B, Blodow N, Beetz M. Fast point feature histograms (FPFH) for 3D registration[C]//Proceedings of IEEE International Conference on Robotics and Automation, 2009: 3212-3217.

[8] Pang G, Neumann U. Training-based object recognition in cluttered 3D point clouds[C]//Proceedings of IEEE International Conference on 3D Vision, 2013: 87-94.

[9] Salti S, Tombari F, Di Stefano L. SHOT: unique signatures of histograms for surface and texture description[J]. Computer Vision and Image Understanding, 2014, 125: 251-264.

[10] Tombari F, Salti S, Di Stefano L. Unique signatures of histograms for local surface description[C]//Proceedings of European Conference on Computer Vision, 2010: 356-369.

[11] Cirujeda P, Mateo X, Dicente Y, et al. MCOV: a covariance descriptor for fusion of texture and shape features in 3D point clouds[C]//Proceedings of IEEE 2nd International Conference on 3D Vision (3DV), 2014, 1: 551-558.

[12] Hariri W, Tabia H, Farah N, et al. 3D face recognition using covariance based descriptors[J]. Pattern Recognition Letters, 2016, 78: 1-7.

[13] Kasaei S H, Tomé A M, Lopes L S, et al. GOOD: a global orthographic object descriptor for 3D object recognition and manipulation[J]. Pattern Recognition Letters, 2016, 83(3): 312-320.

[14] Kechagias-Stamatis O, Aouf N. Histogram of distances for local surface description[C]//Proceedings of IEEE International Conference on Robotics and Automation (ICRA), 2016: 2487-2493.

[15] Romero-Gonz C, Mart J, Garc I, et al. Binary patterns for shape description in RGB-D object registration[C]//Proceedings of IEEE Winter Conference on Applications of Computer Vision (WACV), 2016: 1-9.

[16] Yang J, Cao Z, Zhang Q. A fast and robust local descriptor for 3D point cloud registration[J]. Information Sciences, 2016, 346/347: 163-179.

[17] Bae K H, Lichti D D. A method for automated registration of unorganized point clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2008, 63(1): 36-54.[18] Gelfand N, Mitra N J, Guibas L J, et al. Robust global registration[C]//Proceedings of Symposium on Geometry Processing, 2005, 2(3): 5.

[19] Rusu R B, Blodow N, Marton Z C, et al. Aligning point cloud views using persistent feature histograms[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, 2008: 3384-3391.

[20] Petrelli A, Stefano L D. A repeatable and efficient canonical reference for surface matching[C]//Proceedings of IEEE Second International Conference on 3D Imaging, Modeling, Processing, Visualization and Transmission (3DIMPVT), 2012: 403-410.

[21] Ke Y, Sukthankar R. PCA-SIFT:a more distinctive representation for local image descriptors[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004, 2: 506-513.

[22] Guo Y, Bennamoun M, Sohel F, et al. A comprehensive performance evaluation of 3D local feature descriptors[J]. International Journal of Computer Vision, 2016, 116(1): 66-89.

Extended point feature histograms for 3D point cloud representation

ZHUANG Zhiyun, ZHANG Jun, SUN Guangfu

(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Local feature extraction plays an important role in related point cloud applications. Therefore, an EPFH (extended point feature histograms) descriptor for the local feature representation of 3D point cloud was proposed. Each point pair was represented by several invariant pairwise point attributes. Then, a local reference frame was defined for a keypoint and the neighboring points of the keypoint were transformed into the local reference frame. These pairwise points attributing between the neighboring points and the keypoint were accumulated into several sub-features in a set of subspaces. These sub-features were finally concatenated and compressed into an overall feature descriptor. The EPFH descriptor was tested by a popular publicly available Bologna dataset and was compared with several existing methods. Experimental results show that the proposed EPFH method outperforms several existing methods under different levels of noise and point cloud resolutions.

point cloud; local feature; feature representation; point sets; feature histograms

10.11887/j.cn.201606020

2016-05-19

国家自然科学基金资助项目(61471371)

庄祉昀(1986—)，男，福建南安人，博士研究生，E-mail：jy00842031@163.com； 孙广富(通信作者)，男，研究员，博士，博士生导师，E-mail：sunguangfu_nnc@163.com

TN95

A

1001-2486(2016)06-124-06

http://journal.nudt.edu.cn