GEO螺旋巡游轨道的相对运动分析和螺旋环设计*

郑乐天，周海俊

0　引　言

GEO螺旋巡游轨道[1-2]采用螺旋巡游方式，以不同的构型“上下浮动”在GEO轨道附近，实现对该轨道上空间目标和空间环境的高精度探测.为了能够在确保完成探测任务的同时，避免出现碰撞危险，本文在对GEO轨道上航天器的运动规律分析的基础上，对螺旋巡游轨道与GEO目标之间的相对运动规律进行研究，提出平面螺旋环和三维螺旋环的具体设计方法.

1　GEO轨道上航天器的运动

为实现与地面点相对静止，GEO轨道上的航天器卫星在地心赤道坐标系下的地心距、赤经、赤纬(r,α,δ)需要满足[3]

(1)

将地球近似为三轴椭球体，可获得地球引力位函数为

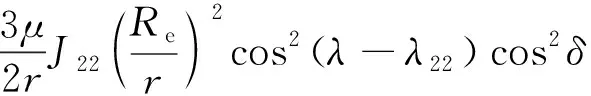
(2)

其中:μ=3.986×1014m/s为地球引力常数；r为卫星的地心距；Re为地球赤道半径；λ为卫星的星下点地理经度；δ为卫星星下点的纬度；J2=1.082 63×10-3为地球旋转椭球项;J22=-1.082×10-6为三轴椭球项；λ22=-14.9°.

将上述位函数代入式(1)的静止条件求解，可知只有在75.1°、165.1°、255.1°和345.1°经度上空，航天器才能实现自然对地静止，其他经度上空的航天器如果不施加控制力，将会沿东西(经度)方向和南北(纬度)方向漂移，其中切向代表经度方向漂移，径向代表南北方向的漂移.

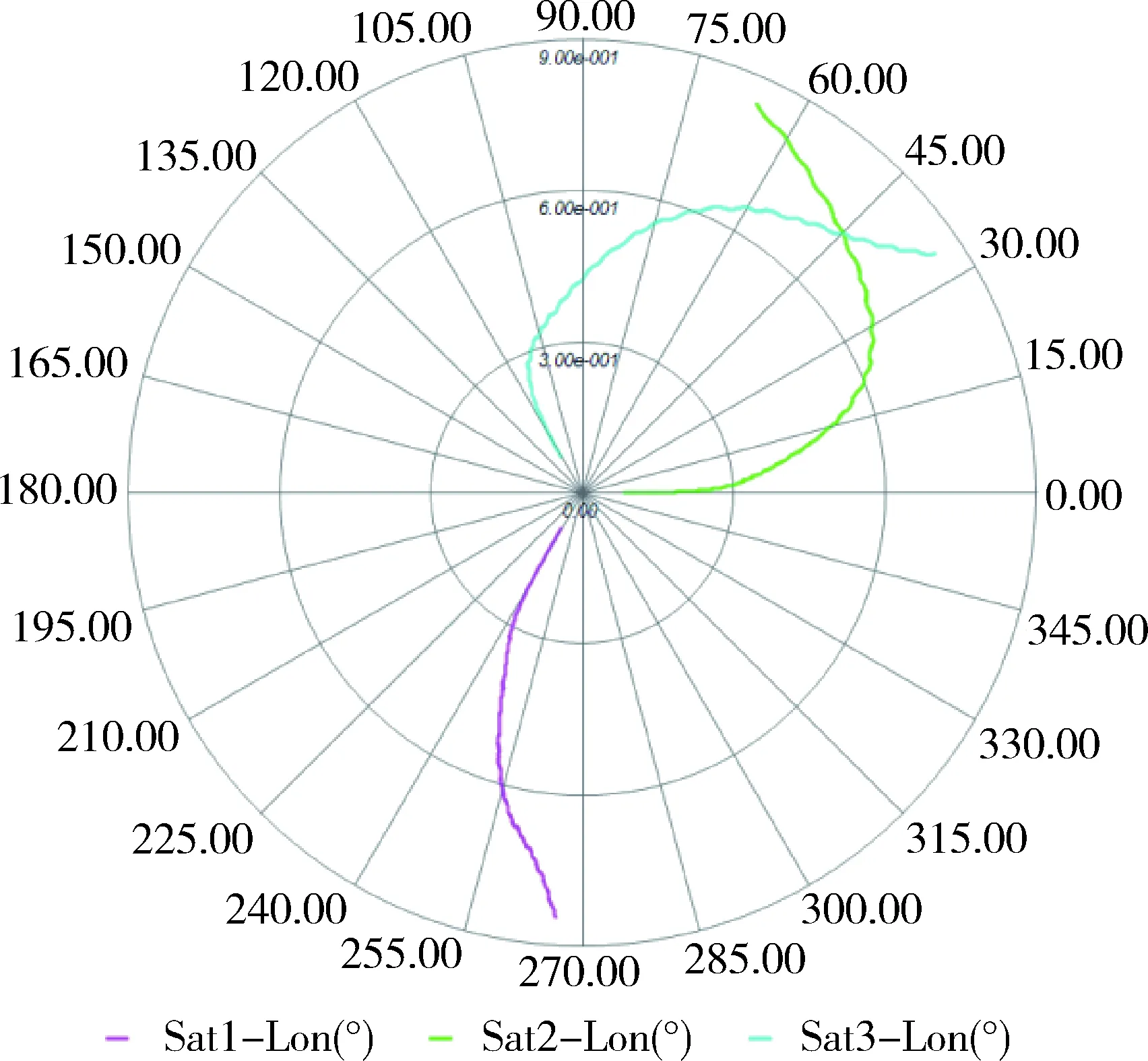
图1　定点在0°E、120°E、120°W卫星一年内东西、南北漂移Fig.1　Position drifts of satellite located in 0°E、120°E、120°W

虽然绝大多数经度上空的航天器都不能实现自然的对地静止，但是，由于航天器的漂移相对缓慢，实际应用中只需要稍加控制就可以实现对地静止，根据相关文献资料[4-6]，一年内GEO轨道航天器保持需要消耗的能量约为

Δv=53.66Δi+2.1

(3)

式(3)等式右边前一项用于南北方向漂移的修正，后一项用于经度方向漂移的修正.

2　相对运动分析

螺旋巡游轨道的轨道根数与目标轨道之间存在微小偏差，这个偏差使得巡游轨道上的航天器能够以一定的距离、方位实现对目标轨道的遍历探测.设螺旋巡游轨道在历元时刻的轨道根数为a,e,i,Ω,ω,tp,分别对应轨道长半轴、偏心率、轨道倾角、升交点赤经、近地点幅角和过近地点时刻.螺旋巡游轨道与目标轨道的轨道根数之间的偏差很小，Δa=a-as,as为目标轨道半长轴，e,i均为小量，作如下近似:

e2≈0,e·Δa≈0,sini≈i,cosi≈1

(4)

在上述近似条件下，螺旋巡游航天器相对于目标轨道的运动方程[4]

(5)

其中，Δr、ΔT和ΔN分别为螺旋巡游航天器相对于目标轨道初值在径向、经度方向和纬度方向的偏差,ωe为地球自转角速度.

由上式可知，当Δa≠0,e≠0时，螺旋巡游轨道相对于目标轨道的运动具有如下特点：

(1) 由Δr可知，在地心矢径方向上巡游航天器处于近地点时，与目标轨道的偏差为Δrp=Δa-eas;远地点时与目标轨道的偏差为Δra=Δa+eas.

当满足Δrp<0<Δra条件时，螺旋巡游轨道相对于目标轨道在目标轨道平面形成交叉的相对运动轨迹.

(2) 由ΔT可知，巡游航天器沿经度方向漂移，漂移速度为

(6)

当Δa>0时，向西漂移；Δa≤0时，向东漂移.

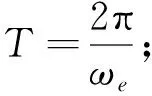
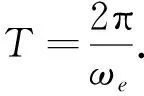
3　螺旋环设计

前面分析已知，满足一定条件下螺旋巡游轨道相对于目标轨道在目标轨道平面内具有交叉点.螺旋环定义在为巡游航天器两次经过同一个交叉点之间的路径.

根据《无线电规则》的规定，GEO轨道航天器的允许运动范围为以定点经度为中心，东西±0.1°，南北±0.1°的范围[6]，因此需要进行螺旋环设计，在满足任务要求的同时，保证航天器之间的安全，避免相互碰撞.

3.1　平面螺旋环设计

平面螺旋环是螺旋环在目标轨道平面内的投影，图2给出了螺旋巡游轨道(东进)的平面螺旋环以及该轨道与目标轨道之间的几何关系.本节主要对平面螺旋环的绕飞时间和绕飞距离进行设计.

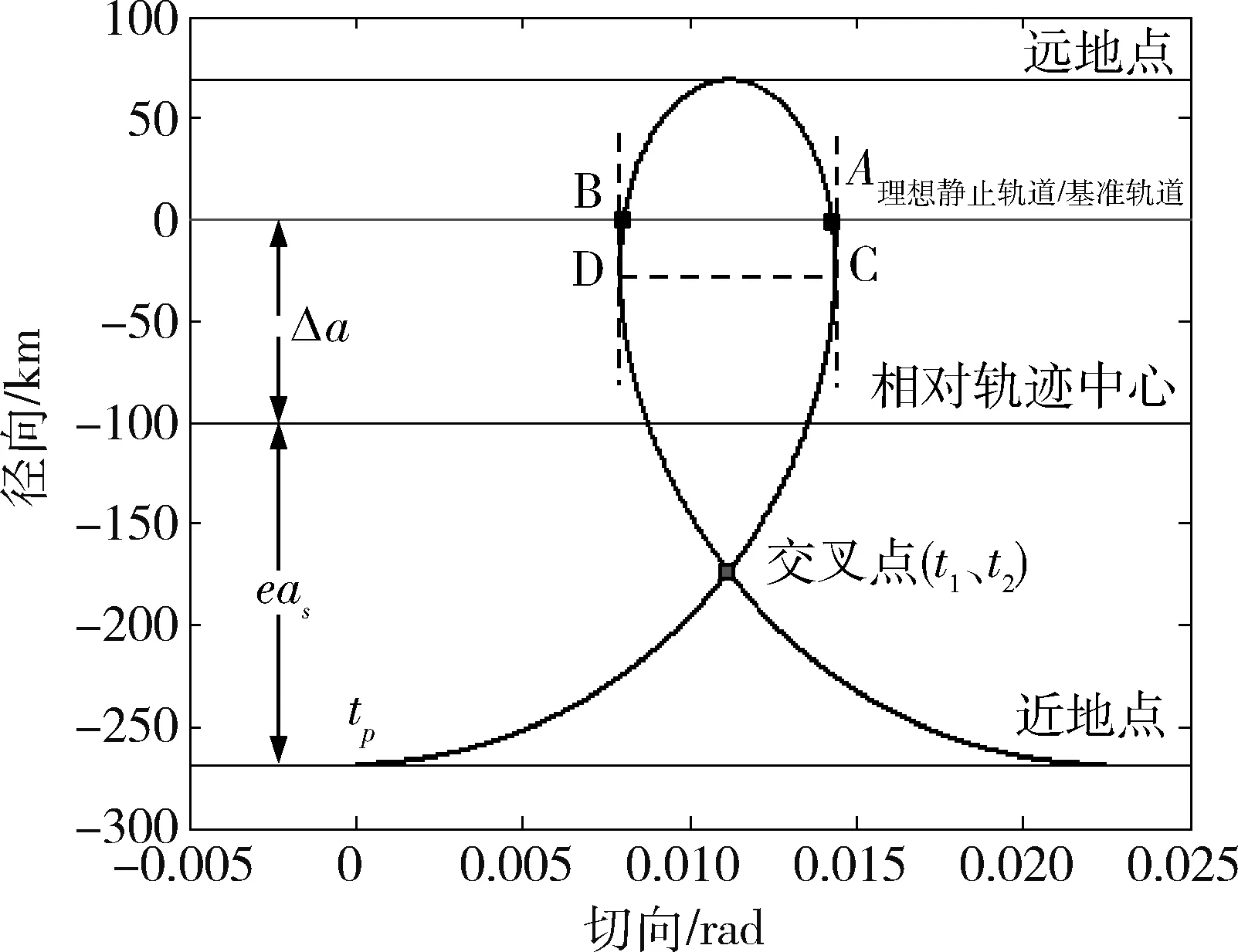
图2　东进螺旋巡游轨道的平面螺旋环Fig.2　Planar whorl of eastern helix tourist orbit

(1) 绕飞时间设计

设经过交叉点的时刻分别为t1、t2(t2>t1),根据式(3)，在t1、t2时刻有

(7)

(8)

设Δt=t2-t1,为绕飞时间，可得

(9)

消去变量t1,可以得到

(10)

由上式可知：Δt是螺旋巡游轨道偏心率、半长轴差Δa的非线性函数.

(2) 绕飞距离设计

图2所示，螺旋环在经度方向上的最大距离为C、D两个点之间的距离，对公式(3)中的第二式求导(忽略三阶小项)，得：

(11)

令式(11)等于0，得到

(12)

由C、D对应的时刻可以得出此两点的沿迹向距离近似等于

ΔTmax=|ΔTC-ΔTD|=

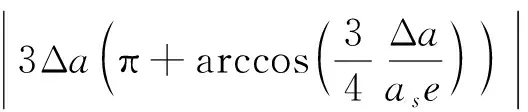
(13)

由公式(13)可知，ΔTmax主要由Δa决定，呈近线性关系.

3.2　三维螺旋环设计

三维螺旋环综合巡游航天器在目标轨道平面内的运动和纬度方向的运动，由于在三维空间内的运动比较复杂，本文只对两种特殊情况进行分析.

(1) 螺旋巡游轨道ω=0°或者180°的情况

根据公式(3)，可知当螺旋巡游轨道ω=0°或者180°时，纬度方向的运动为

ΔN=iassin(ωe(t-tp))

(14)

将式(11)与(3)的第一式联立，可以获得

(15)

即螺旋巡游轨道在目标轨道rN平面内形成椭圆轨迹，结合螺旋巡游轨道在目标轨道平面内的设计，可知，此时可获得三维空间内的螺旋环.设Δa=100 km，i=0.1°，e=0.003，tp=0，仿真时间取2天，则可以得到此时的三维螺旋环如图3所示.

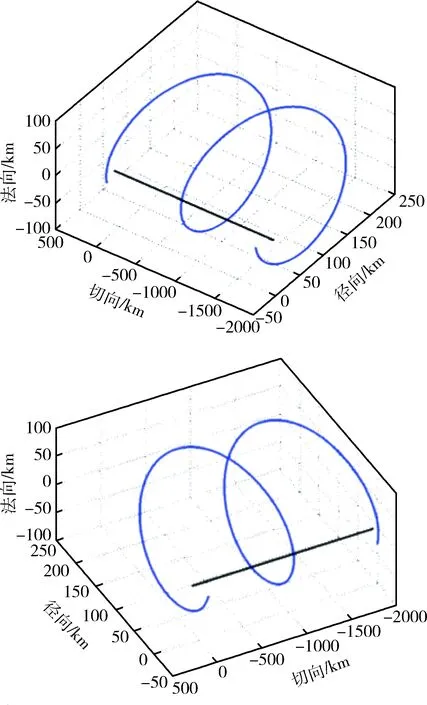
图3　ω=0°或者180°时的三维螺旋环Fig.3　3D whorl when ω=0° or 180°

(2) 螺旋巡游轨道ω=90°或者270°的情况

此时，螺旋巡游轨道在目标轨道rN平面内的轨迹满足

(16)

由式(13)可知，此时螺旋巡游轨道在目标轨道rN平面内的轨迹为直线，取上述相同的仿真条件，可以得到此时三维螺旋环退化为图4所示的平面.

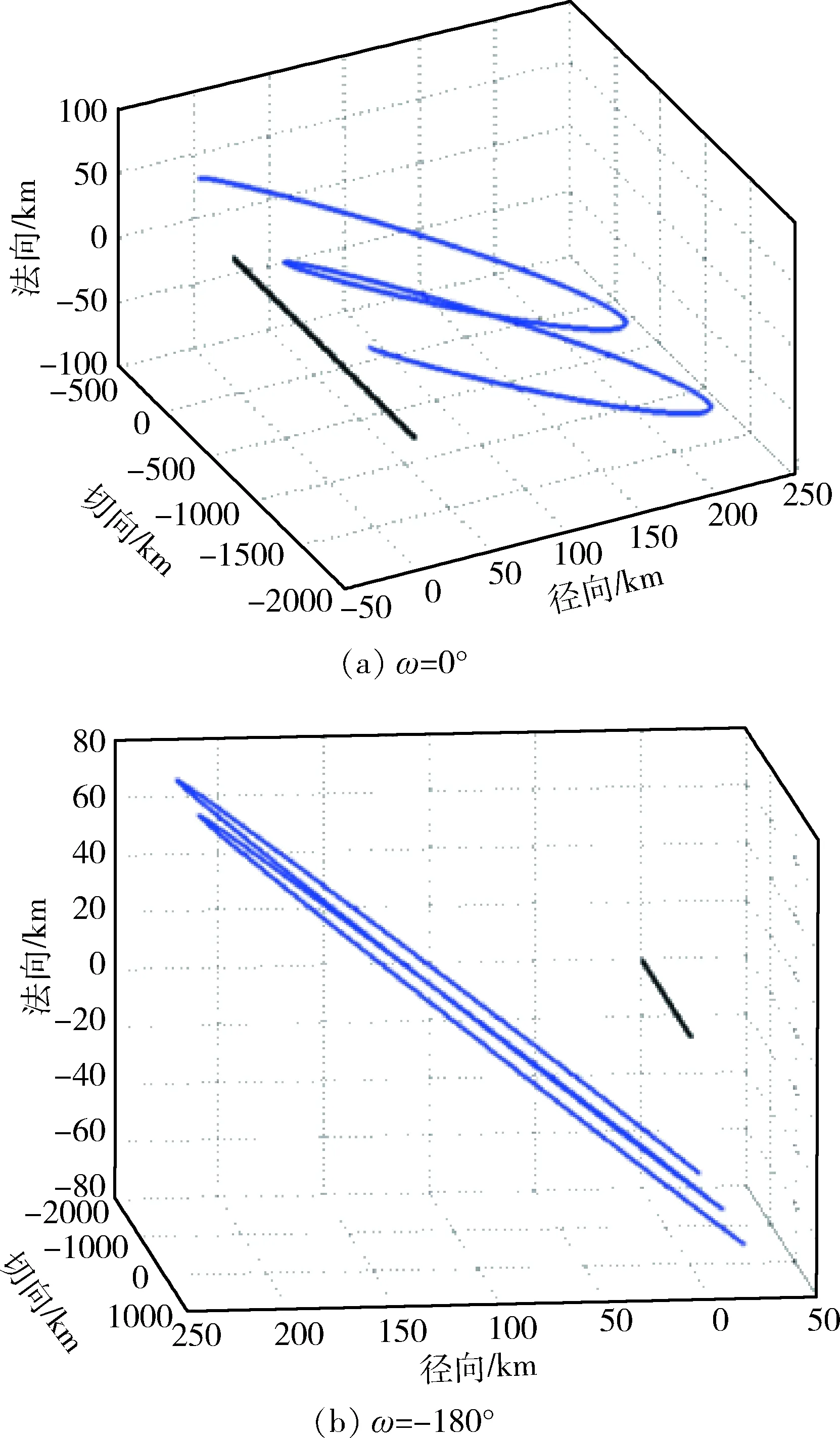
图4　ω=90°或者270°时的三维螺旋环Fig.4　3D whorl when ω=90° or 270°

由前述分析可得：当近地点幅角取0°或者180°时，观测更加全面，但由于巡游轨道与目标轨道平面之间有交点，存在着距离过近的风险；当近地点幅角取90°或者270°时，巡游轨道与GEO轨道平面没有交点，但是不会存在相撞的风险.

4　结　论

GEO螺旋巡游轨道中，螺旋环的设计是其首先需要解决的问题，本文通过相对运动规律的分析，给出了平面、三维螺旋环的基本设计方法.但实际上，由于空间各种摄动的影响，螺旋巡游轨道在空间会逐渐偏离原先的轨道，此时可采用多种方法进行修正，如采用轨道控制或者采用基于摄动补偿的轨道设计方法等.