基于红外波段船载星光定向仪白昼恒星探测技术*

夏梦绮，卢　欣，张春明，孙大开

0　引　言

船载天文导航以自然天体为导航基准，通过光电方式被动探测天体的位置，并结合地平、世界时等信息，最后通过惯性坐标系转换进行地理坐标系下的位置解算.在舰船的天文导航中，相比单陀螺惯性导航方案，“陀螺+星光定向仪”组合能够实现优势互补，可自主导航，具有较广泛的应用需求.其中，惯性导航提供较高精度的测量船水平姿态数据(纵摇和横摇)、中等精度的航向数据和船位数据，星光定向仪经过星图识别和姿态计算，实现对惯性导航航向和船位数据的高精度修正.

现行船载星光定向仪选用近红外波段进行探测.相比可见光波段，测星概率大约高一个数量级，且大气散射更低，透过率更高[1]，在白昼条件下具有更强的恒星探测能力.但其存在背景噪声起伏较大、伪星点坏像素较多等问题，红外白昼恒星探测技术是目前应用中一大难题.

本文针对以上问题，设计了一套比较实用、高效、可用于白昼条件下船载天文导航算法，给出了理论推导和实验验证.

1　算法基础

在舰船天文导航中，星光定向仪在提取和识别恒星后，计算出星光定向仪基准镜系相对惯性系的姿态数据，并利用协调世界时(UTC)、惯性系和地理系三者之间的转换关系，对惯性导航系统测得地理经纬度数据进行修正.其中，由于恒星观测在大气层内进行，观测星矢量混入蒙气差，导航算法需在当地地理坐标系下对恒星天顶角进行蒙气差修正.

1.1　工作原理

图1中，星光定向仪与惯性导航系统形成捷联组合导航系统，星光定向仪在大气层内对空间中的恒星成像，利用算法进行星点提取和星图识别，并利用多帧的方式去除伪星点，惯性导航系统给星光定向仪定时发UTC时间、水平方向(俯仰角和滚动角)数据，星光定向仪根据惯性系和地理坐标系的转换，在蒙气差修正的基础上给出修正后的地理位置和航向角信息，用于惯性导航系统自身修正.

下面根据工作原理流程图，对涉及的算法给出理论计算模型.

图1　星光/惯性组合导航工作原理图Fig.1　The principle of CNS/SINS integrated navigation

1.2　坐标系定义及坐标系转换

(1) 地心赤道惯性坐标系Ci

赤道惯性坐标系又称地心天球参考系(GCRS)，为近地空间坐标系.GCRS以地心为原点，xi轴指向春分点，zi轴指向北天极，yi轴由右手定则确定.

(2) 地心地理坐标系Ce

地心地理坐标系与地球固联，也称国际地球参考系(ITRS).其坐标原点在地心，xe轴指向经纬度为零的点，ze轴指向地北极，ye轴由右手定则确定.位置的测量通常以ITRS为基准.

(3) 当地地理坐标系Cg

当地地理坐标系是用来表示载体位置的坐标系，是水平和航向的基准，也称东北天地平坐标系(ENU).其原点为载体重心，E轴指向正东，N轴指向正北，U轴沿垂线方向指向天.

(4) 星光定向仪基准镜坐标系CJ

该坐标系与对应测量坐标系仅存在一个旋转矩阵，目前算法实验时假定等同于载体坐标系和测量系.恒星在像面的位置(u,v)坐标转换成单位矢量在该坐标系下表示，标定系数在该坐标系下表示.计算的姿态指该坐标系下惯性指向的方向余弦矩阵.

图2　星光定向仪测量原理示意图Fig.2　The measuring principle of star sensor

坐标系间的相互转换为：

(1) 像平面坐标系与基准镜坐标系的转换

已知某星点的位置为(u,v)，根据针孔成像模型，有

(1)

式中，f为星光定向仪的焦距.式中的非线性关系可近似由xS、yS与u、v的高阶多项式描述.

(2) 基准镜坐标系与惯性坐标系的转换

当像平面上出现不少于2颗观测星时，通过导航星匹配算法，基于单帧图像的姿态可由经典的QUEST算法给出[2].两坐标系的转换关系满足

W=CJiV+n

(2)

式中，CJi即为姿态矩阵，n为噪声误差.W和V矩阵分别定义在坐标系CJ和Ci内，即

(3)

其中，WSi=[xSiySizSi]T,Vi=[xiyizi]T.

由于观测星坐标中包含了测量误差，通常需通过姿态解算方法寻找CJi的最优解.

由惯性系下的姿态矩阵，结合UTC时间和水平姿态信息，可以对惯导给出的地理经纬度信息及方位角进行修正.

(3) 惯性坐标系与地心地理坐标系的转换

ITRS转换至GCRS有两种方法，一种是基于春分点的经典转换方法，另一种是基于无旋转原点NRO的坐标转换方法[3].本文采用基于无旋转原点NRO的坐标转换方法，基本转换公式如下：

Ci=Q(t)R(t)W(t)Ce

(4)

式(4)以瞬时天球中间级(CIP)对应的赤道坐标系为中间变换，CIP在GCRS和ITRS坐标系中都会产生旋转矩阵.其中，Q(t)是由于天球中间极CIP在GCRS中的运动而产生的转换矩阵；R(t)是由于地球旋转(将地球星历原点TIO方向旋转至天球中间原点CIO方向)所产生的旋转矩阵；W(t)为极移矩阵，由CIP在ITRS中的运动而产生.具体解算流程详见文献[4].

(4) 当地地理坐标系与地心地理坐标系的转换

约定R1(θ)、R2(θ)、R3(θ)分别为绕x、y、z轴的基元旋转矩阵，已知载体地理经纬度(λ,φ)，则地心地理系到当地地理系的转换矩阵为

Cge=R3(90°)R2(90°-φ)R3(λ)

(5)

以上所述的转换关系可以用图3表示.

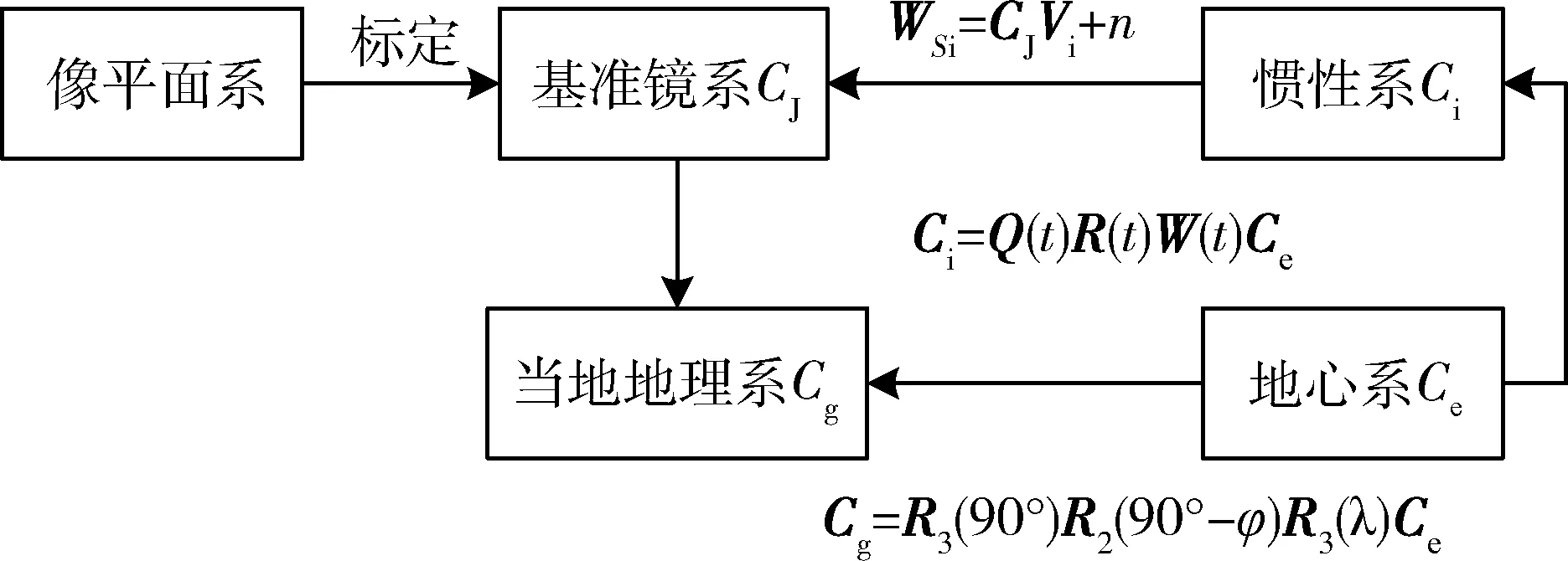
图3　船载星光定向仪坐标系转换关系Fig.3　The coordinate transformation of shipboard star sensor

1.3　蒙气差修正

在大气层内进行天文导航，蒙气差是最主要的误差源.影响蒙气差的因素有很多，如温度、湿度、气压、湍流等，其中观测天顶角是影响蒙气差大小的最主要因素[5].本文根据天顶角与蒙气差的关系，对恒星在当地地理坐标系下的指向进行修正，以基本消除蒙气差引起的观测误差.

已知导航星在惯性系下的矢量Vi，根据上述坐标转换关系(3)、(4)，推导得当地地理坐标系下的矢量Vg=[xgygzg]T.此时修正前的天顶角

h=arccoszg

(6)

根据蒙气差与地理经度λ、地理纬度φ、某月的上中下旬t、海拔高度H和修正前天顶角h的关系表格table，利用蒙气差查表法得到天顶角修正量dh，蒙气差查表法公式近似如下：

dh=table(λ,φ,t,H,h)

(7)

修正后的天顶角h′=h+dh.进而得到Vg修正后的矢量为

(8)

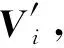
1.4　位置与航向计算

基准镜系相对当地地理系的角位置可通过按3-1-2转序旋转得到的3个欧拉角表示，即

CJ=R2(φ)R1(θ)R3(ψ)Cg

(9)

在静态观星实验条件下，基本可以保证星光定向仪水平放置，可取θ=0、φ=0.结合式(5)，近似有：

CJ=R3(ψ)R3(90°)R2(90°-φ)R3(λ)Ce

(10)

利用QUEST方法已求解出姿态矩阵CJi，通过坐标转换关系(3)得到视轴在地心地理系下的姿态CJe.则经度、纬度和方位角可分别表示为

(11)

2　算法实现技术方案

星光定向仪对空间恒星成像，经质心计算得到天体在像平面中的位置，并由坐标系转换关系求得恒星在载体系下的观测矢量.根据光轴粗指向和导航星表搜索导航星，通过星图识别将导航星与观测星匹配.利用导航星信息、观测星信息及时间信息可以精确计算出载体的位置与航向.

红外探测虽然比可见光有很大优势，但也存在多项问题.观星实验过程中出现4个主要问题：红外星图背景噪声；图像存在伪星点；红外芯片存在坏像素；算法需适应一定的灰度背景范围.

为解决上述问题，设计实现了4个技术方案，可实现白昼红外探测，提升探测概率.算法实现框图如图4所示.

图4　船载星光定向仪算法实现流程图Fig.4　The flow chart of algorithm of shipboard star sensor

2.1　星图噪声滤波算法

恒星在像平面上一般表现为近似圆形的点状光斑，光斑直径大小通常为3～5个像元，多次平均后的光斑能量近似高斯分布[6].然而，星点目标形貌极易受噪声的影响，导致偏离[7].对星图进行滤波，抑制背景噪声，是实现高精度质心定位的重要条件.

图5为星光定向仪采集的局部原始图像.红外星图图像噪声可分为3类，包括探测器噪声、读出噪声和光子噪声.探测器噪声包括固定模式噪声、暗电流随机噪声、暗电流非一致性、像素响应非一致性和随机热噪声等.其中，固定模式噪声、暗电流非一致性、像素响应非一致性可通过噪声修正去除，除光子噪声外，其他噪声可通过探测器致冷的方式降低[8,9].

图5　观星实验局部原始图像Fig.5　The part original image for a stellar observation test

实际嵌入式系统主要对固定模式噪声进行修正，本文采用简化模型将上一帧图像的列均值作为当前帧图像的固定模式噪声，当前帧图像在去除固定模式噪声的基础上，利用相邻两行图像灰度的背景噪声具有相关性逐行计算背景阈值.

算法中的背景阈值描述：

T=μ+α·σ

(12)

式中，T为当前行的背景阈值，μ为上一行的均值，σ为上一行的方差，α为方差系数，通常取2.0～3.5.具体的α取值按照T的取值范围动态调整，由DSP计算后写入FPGA.

经过阈值扫描处理后，提取每行超过阈值的像元作为有效像素.实际白昼观星的图像中提取出的大部分有效像素为单像素背景噪声，为此对连通域二次扫描算法进行改进，增加了单像素滤波扫描算法去除孤立噪声.该算法基本流程如下：

1) 对所存储的像元进行行内分析，扫描当前行是否有其≥2个像元的连通域存在；

2) 再对该像元进行行间分析，遍历下一行是否有其≥2个像元的连通域存在；

3) 若都不满足，将连通域=1个像元的单个像素的灰度标记为-1，以剔除单像素噪声.

图6为滤波算法修正后的有效像素直方统计图，可见，星点信号灰度明显高于其他像素，且近似呈正态分布.

图6　有效像素直方统计图Fig.6　The histogram of effective pixels

2.2　多帧伪星点剔除算法

经噪声修正后的图像中提取的星点分为3种：恒星、空中飞行颗粒、响应异常的像素.对伪星点的判断依据如下：

思维型学习疑难也称组织型学习疑难，它是在信息的组织时出现的异常情况而产生的学习疑难．美国学者安东尼·格里高根据知觉的具体与抽象，规则的次序与随机将人类的思维分成了四种：具体而有序的思维、抽象而有序的思维、具体而随机的思维、抽象而随机的思维[25]．这四种思维类型并无好坏之分，但它们之间的思维形式有所不同[26]．不同的思维形式在一方面表现出一些优势的同时，往往在另一方面会表现出劣势，以致于出现一些思维障碍，从而产生思维型学习疑难．

1) 恒星在视场内随着地球自转运动，运动的角速度较慢，且在像面上成像形状规则；

2) 空中飞行颗粒在视场中运动速度较快，且物距位置不固定，成像后有离焦现象，与恒星成像形状存在差别；

3) 像面中响应异常的像素位置固定，由像素响应的非一致性引起，与正常像素响应差别明显，有光照时处于饱和或接近饱和的状态.

红外芯片坏像素较多，将作为主要干扰目标影响恒星识别.利用上述不同星点的运动特点，采用连续多帧比对的方式可以有效去除.多帧算法策略的基本流程如下：

1) 取N帧图像为一组，记录每一帧图像提取的所有星点的(u+v)坐标，并按升序排列；

2) 统计相邻(u+v)的差值小于0.2个像元的累计次数与其对应的索引位置，连续出现3次以上则认为是坏像素，从星点序列中剔除；

3) 逐步扫描相邻两帧，若存在星点满足

Δu2+Δv2<6.5

图7为多帧处理前后有效星点的统计图.由图可见，多帧算法策略能有效剔除坏像素，提取真实星点.

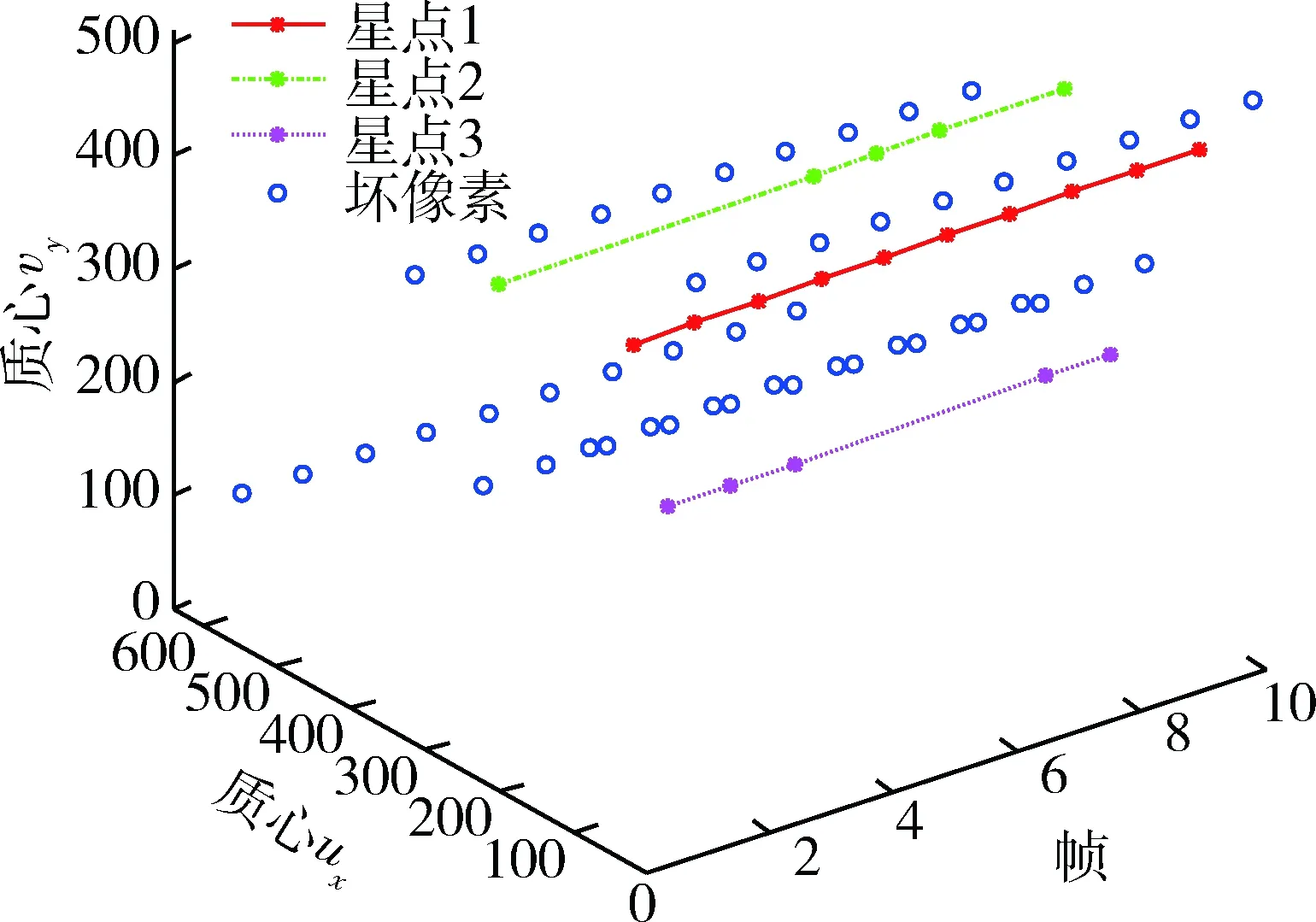
图7　多帧处理前后星点统计图Fig.7　The statistical stars chart before and after multi-frame process

2.3　坏像素索引表

实际系统中，每一组图像均采用多帧算法剔除坏像素将极大影响算法运算速度.由2.2分析可知，像面中响应异常的像素位置固定，因此存储所有坏像素的像平面坐标，并在星点提取阶段就对星点进行伪星判断，能够有效简化算法流程.具体判断过程如下：

1) 将所有坏像素的(u+v)坐标按升序排列，以(u+v)坐标间隔50为区间建立索引表，1～50索引为1，50～100索引为2，以此类推；

2) 计算星点的(u+v)坐标，判断其索引；

3) 将星点的像平面坐标分别与该索引内的坏像素的作差，当差值满足：

则认为该星点是表中坏像素，将其从星点序列中剔除.

2.4　积分时间自动梯度调整算法

图像灰度范围为0～1 023，当图像达到非线性工作区(灰度800～1 023)时无法观测到恒星，观星算法需要适应一定的灰度背景范围.实测白昼条件下积分时间与图像灰度均值的拟合关系如图8所示，有如下说明：

1) 当积分时间为0时，图像灰度均值为225，此数值为模数转换器设置的偏置量；

2) 在积分时间<5 ms的情况下，图像灰度增量随积分时间线性增加；

3) 当积分时间>5 ms时，探测器像素接近满阱，图像灰度随积分时间的增加而缓慢增加.

在实际积分时间自动调整算法设计中，根据该线性关系和当前背景灰度，有积分时间调整公式

T=k(DN)T0

(13)

式中:T0为当前时刻积分时间，默认初始化设置为2 ms；k为调整系数，在灰度250～700之间梯度设置为1.01～1.2；T为下一时刻积分时间.

根据式(13)设置下一时刻的积分时间，最终调整至合理灰度区间(灰度650～700).

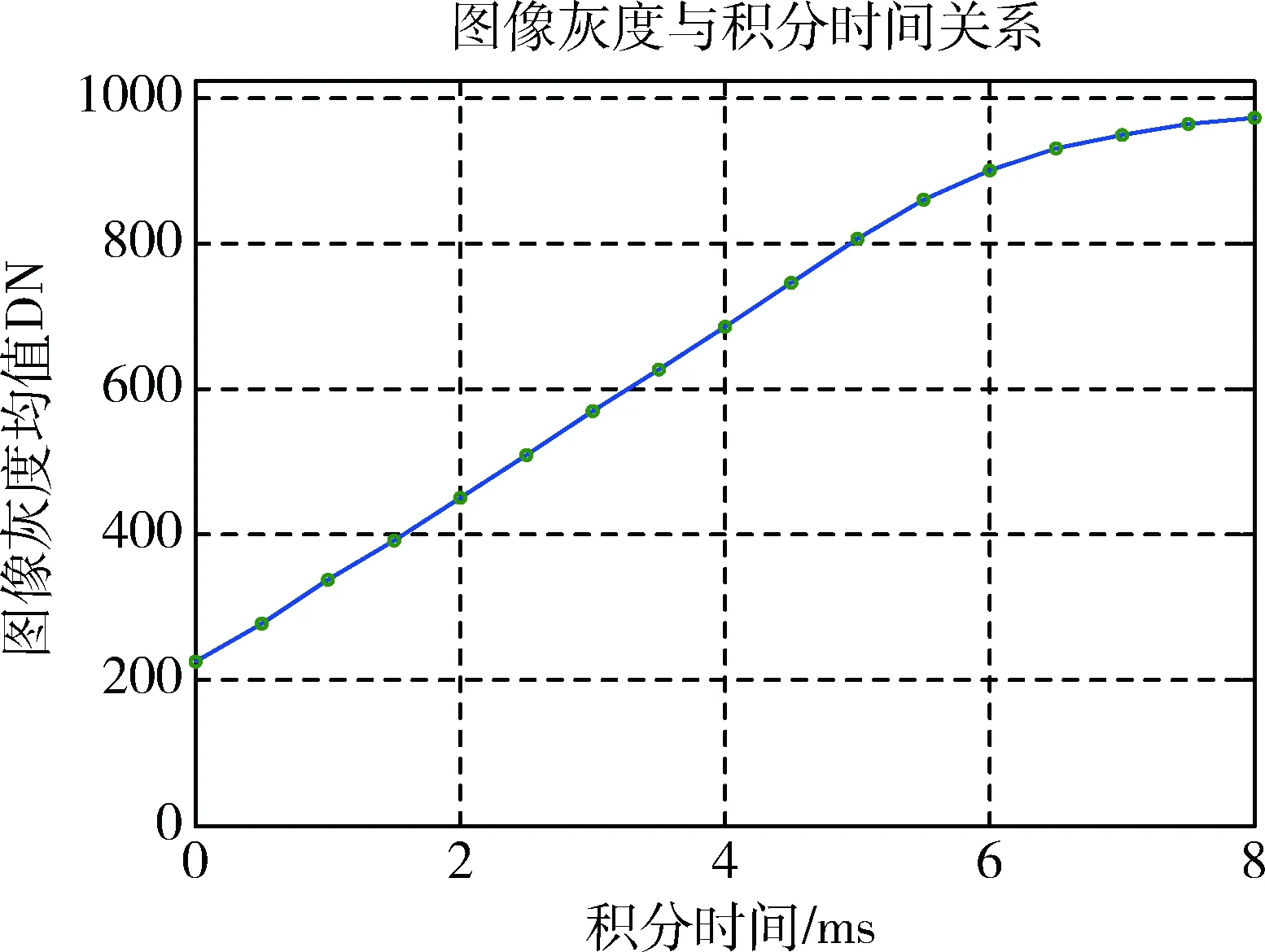
图8　图像灰度与积分时间关系Fig.8　The curve of image gray with different integral time

3　实验及分析

船舶平台星光定向仪的系统参数如表1所示.

表1　船舶平台星光定向仪参数Tab.1　The parameters of shipboard star sensor

采用红外波段2MASS(two micron all sky survey)星表作为原始星表[10].实验前将星光定向仪水平静止放置于地面，此时可认为载体水平倾角为(0°,0°).测量载体地理经纬度的初值为(λ0,φ0)=(117°13′7″E, 38°48′10″N)，方位角为ψ=121.112 0°.

选取了2017年1月20日18:07～18:08采集的图像作为实算数据.取10帧图像为一组，图9为连续60次外场实验的经度、纬度和方位角计算结果.统计结果显示：算法的定位误差为(Δλ,Δφ)=(12.101 3″, 16.241 8″)，航向误差为Δψ=9.353 7″.

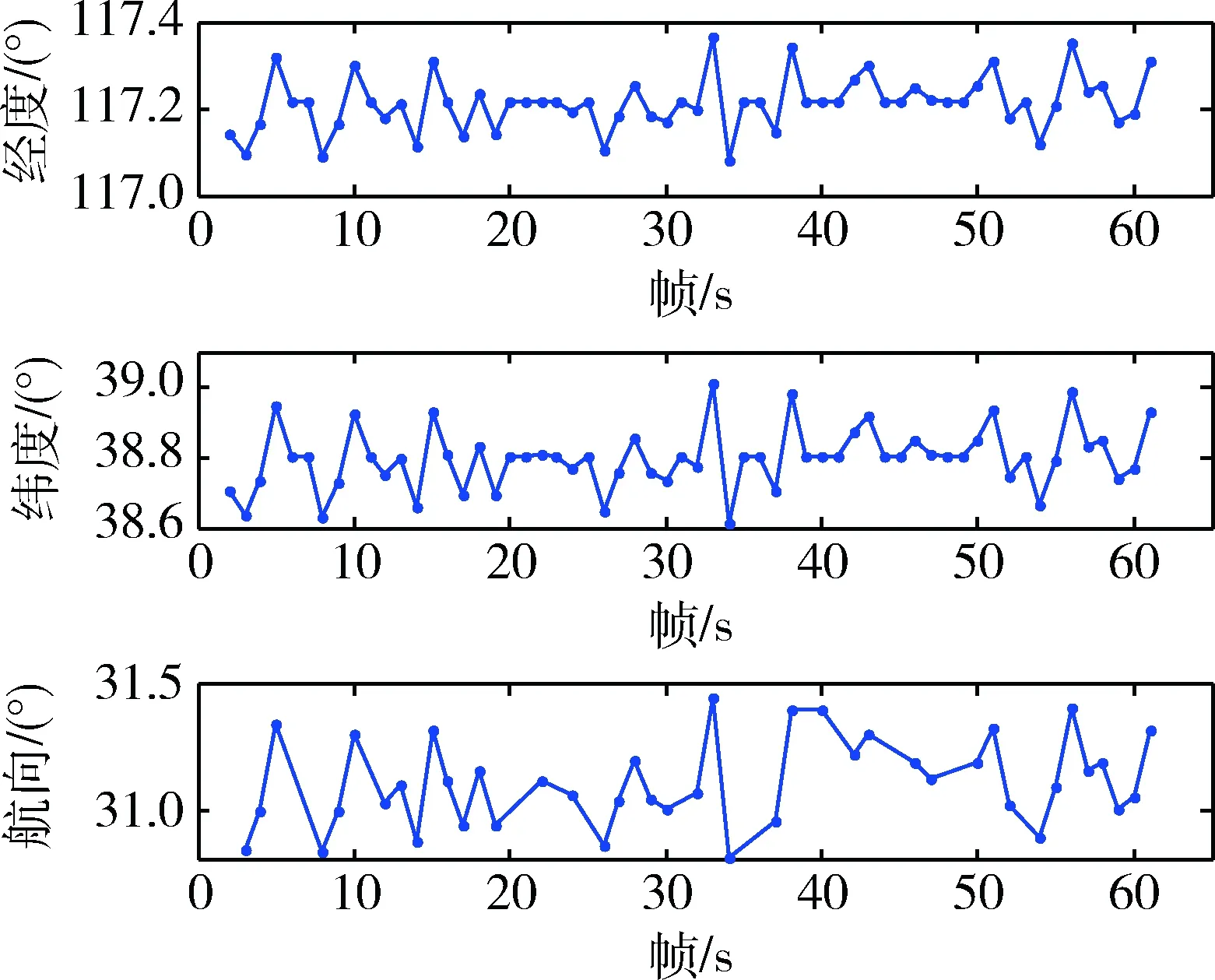
图9　位置与航向计算结果Fig.9　The results of position and orientation

实验结果表明，本文的算法能够利用外场实验拍摄的星图计算出较准确的位置与航向信息.

4　结　论

本文根据星光定向仪工作原理给出了基于红外探测的船载白昼恒星探测技术方案.该技术实时修正了蒙气差项，使用自动梯度调整算法增强背景的适应性.针对红外探测特有的帧间噪声波动大、伪星点及坏像素多等问题，使用滤波算法降低了帧间噪声影响，使用多帧伪星点剔除算法有效剔除了伪星点，并建立了坏像素列表.实地外场实验验证了天文导航算法有效性和精度，表明算法能从拍摄的红外星图中提取星点信息，并解算出载体地理位置和航向角，有较高精度，已具备一定的理论和实际应用价值.