控制力矩陀螺框架谐波减速驱动系统建模与仿真*

杜　航，李　刚，鲁　明

0　引　言

框架驱动组件是控制力矩陀螺的关键组成部分之一，用于驱动转子组件绕框架轴旋转以输出控制力矩，实现航天器的姿态控制与姿态机动.框架组件的性能直接决定了输出力矩的精度、响应速度与平稳性，直接影响航天器的姿态控制性能.采用谐波减速器作为传动机构的CMG框架具有体积小、重量轻、功耗低等优点，但不可避免地会带来由于传动精度、齿隙、刚度非线性特性等问题引入的传动误差.为此，建立充分描述谐波减速器特有性能的控制模型对研究采用谐波减速器的CMG框架系统传动精度问题具有重要作用.

在目前对采用谐波减速器作为传动装置的间接驱动的CMG框架驱动系统的研究中，文献[1]针对CMG框架伺服系统产生的谐振问题，提出了一种基于H∞混合灵敏度的振动抑制方法；文献[2]针对CMG框架系统谐振，建立了带有速度环的CMG框架动力学模型，但以上所建立的CMG框架模型中，针对谐波减速器只考虑了减速比和固定转速下的刚度，对于齿隙和减速器非线性扭转刚度等非线性因素没有考虑.文献[3]针对谐波减速器的迟滞特性建立了一种数学模型，并针对这一特性进行了仿真研究.文献[4-5]针对采用电机直驱的CMG框架伺服系统进行了建模.文献[6]对大型单框架CMG进行了整体仿真，考虑了谐波减速器但是所建立的模型并没对减速器的回差、非线性扭转刚度、传动刚度等现象进行研究.

本文对CMG框架驱动组件用谐波减速器进行了精细的建模，在谐波传动系统线性模型的基础上，充分考虑了谐波减速器的齿隙模型、非线性刚度、减速器效率等因素.针对低速下谐波减速器的低刚度特性所引起的传动误差较大提出了考虑传动误差的减速器模型；最后建立了CMG框架驱动系统模型，并对谐波减速器刚度和阻尼这两个因素对框架系统性能的影响做了研究.

1　直接驱动和间接驱动方式比较

根据国内外研究现状，框架驱动系统有直接驱动和间接驱动两种方式，其性能对比如表1所示.

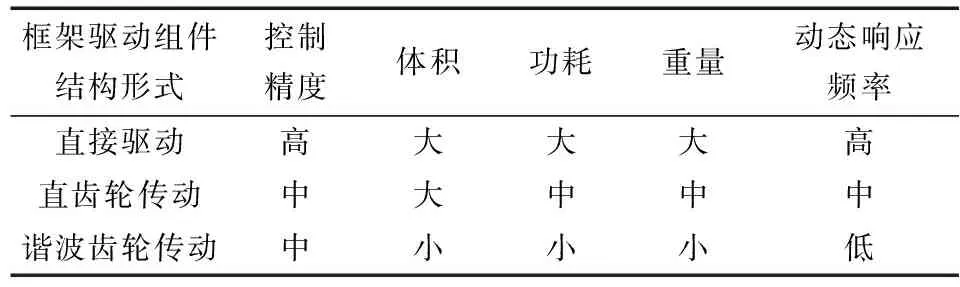
表1　框架驱动组件驱动方式性能对比Tab.1　Performance comparison of frame-driven component drive mode

由表1可知采用直接驱动形式的框架驱动系统，由于输入轴与输出轴之间一般采用刚性连接，不会引入传动误差，因此具有刚度高、测量精度高，框架动态响应频率高的优点.但是由于没有减速环节，所选用的电机力矩系数大，从而会产生电机与框架驱动组件的结构尺寸大、重量大等问题.间接驱动的框架驱动组件在驱动电机与输出轴之间一般选用谐波齿轮或直齿轮作为减速机构进行减速，框架转速的转速较低，不可避免的引入由于传动精度、回差等因素引入的传动误差，但采用间接驱动形式的框架驱动组件具有体积小、重量轻、功耗低、抗干扰能力强等优点.本文所研究的1 000 N·m·s控制力矩陀螺采用谐波减速器作为减速机构.

2　谐波减速器建模

2.1　谐波减速器线性建模

CMG框架系统中谐波减速器的作用是将框架电机的转速以一定的传动比减速并将框架电机的输出力矩放大后驱动框架——转子系统旋转的组件，谐波减速器要具备较大的减速比，而且要求扭转刚度大、反向间隙小、摩擦力矩小等特点.谐波减速器由柔轮、波发生器和刚轮3部分组成，这3部分可以以一个为固定端，其他两个中的一个作为输入端、另一个作为输出端，从而实现增速或减速.本文所研究的1 000 N·m·s控制力矩陀螺框架驱动系统中的谐波减速器所采用的传动方式为：刚轮为固定端，电机驱动波发生器主动运动，柔轮为从动.

根据谐波齿轮传动原理，可将谐波传动系统简化为典型的二质量系统[7-8]，中间由弹性轴连接.CMG框架驱动系统所采用的谐波传动系统线性模型如图1所示.

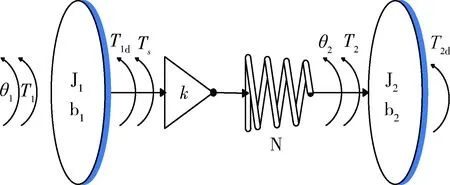
图1　谐波传动系统线性模型Fig.1　Simplified model of harmonic drive system

其中，θ1为电机端角位移，θ2为负载端角位移(即谐波齿轮输出角位移)，T1为电机输出力矩，T2为谐波齿轮柔轮输出力矩，J1为伺服电机转动惯量，J2为负载转动惯量，Ts为电机输出到谐波齿轮柔轮的力矩，T1d为电机端扰动，T2d为负载端扰动，b1、b2为粘性摩擦系数，k为谐波减速器刚度，N为谐波减速器传动比.

根据图1所示CMG框架驱动系统线性模型，根据力学关系，可以得到力矩平衡方程

(1)

由减速器传动比可以得出电机输出到谐波齿轮柔轮的力矩和柔轮的输出力矩

(2)

根据上述方程(1)～(2)即可建立CMG框架驱动系统线性模型.

2.2　谐波减速器齿隙死区模型

齿隙的死区模型被广泛地应用于描述传动的控制系统中齿隙的非线性特性，其模型描述如下：

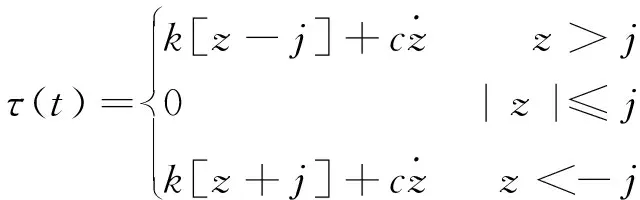
(3)

式中，z=θm(t)-iθd(t).

其中，k为谐波减速器刚度，c为谐波减速器阻尼，j为齿隙，z为输入的相对位移.

齿隙死区模型的输入是减速器输入与输出端的相对位移，输出是减速器输出端传递到负载上的力矩，其中综合考虑了减速器刚度和阻尼这两个非线性因素对齿隙的影响，通过驱动系统和从动系统的传递力矩来描述齿隙.

利用MATLAB/Simulink软件对齿隙死区模型进行仿真，得到反映输入转角相对位移和输出力矩之间关系的齿隙死区模型，如图2所示.图3模拟了正弦信号通过齿隙死区模型的输出.由图3可以看出，利用正弦函数来模拟框架转速方向从正转到反转的变向过程，此时输出力矩在转速变向处，即正弦函数的零点处，会出现延迟.

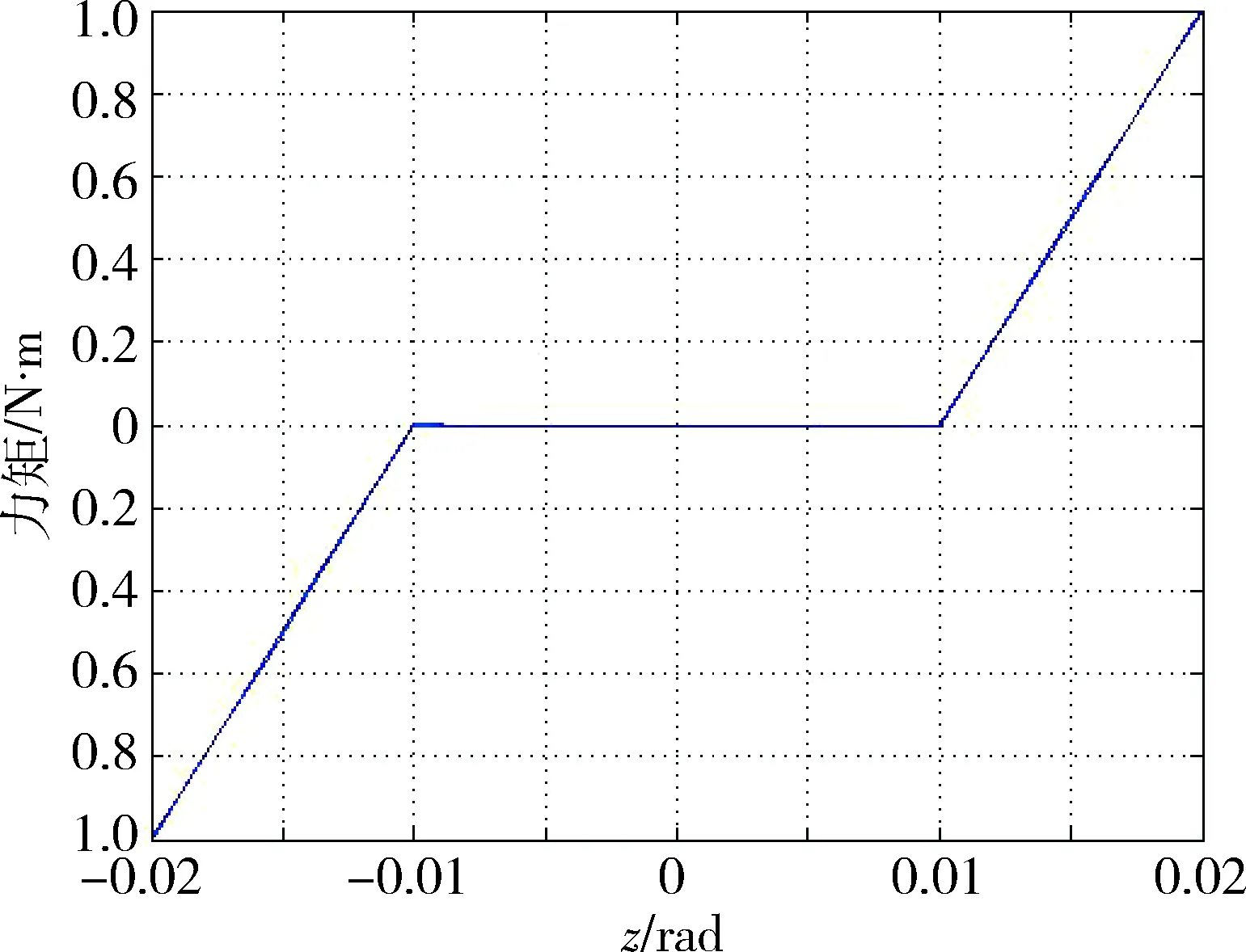
图2　齿隙死区模型Fig.2　Dead-zone model

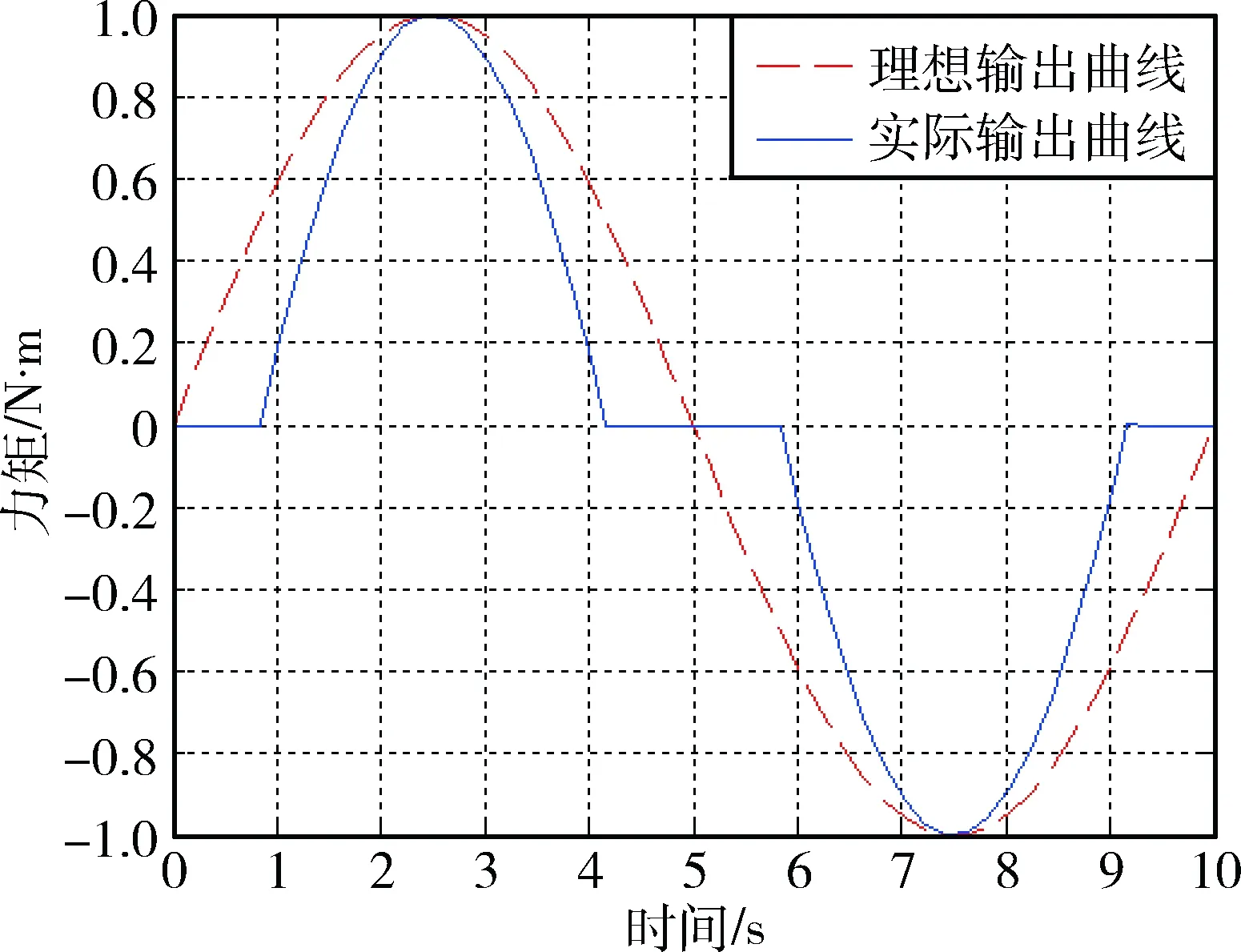
图3　正弦函数通过模型的输出Fig.3　Sinusoidal signal passes through the model

2.3　考虑传动误差的减速器模型

传动误差的定义如下：

(4)

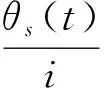
但由于在具有正反转运动的谐波齿轮传动中，存在着制造误差、传动刚度、外界负载的误差、齿隙回差等诸多影响传动误差的非线性因素，故式(4)并不能直接应用于谐波减速器传动误差的计算.考虑到具有正反转运动的谐波齿轮传动误差公式如下[9]：

(5)

式中，Δφhg为谐波传动中的转角误差，kB是实际测量传动误差值与传动误差理论计算值的比值；zmp是谐波齿轮同时参与啮合的齿对数；ΔF∑j是刚轮或柔轮的综合误差；d′是转动齿轮的分度圆直径；U为波发生器波数；ω0是柔轮的最大径向变形量；ih是谐波齿轮的传动比；Δpn是波发生器零件的径向误差；Δe是弹性回差的理论值.

根据式(5)的传动误差公式可以建立谐波减速器传动误差模型，与(1)～(3)联立可以建立考虑传动误差的减速器模型，并与不考虑传动误差的减速器模型进行对比.

取转速n=1 rad/s(模拟低速)和n=1 000 rad/s(模拟高速)进行仿真，结果如图4所示.

图4(a)表示在低速下不考虑传动误差的减速器模型，图4(b)表示在低速下考虑传动误差的减速器模型，图4(c)表示在高速下不考虑传动误差的减速器模型，图4(d)表示在高速下考虑传动误差的减速器模型.通过对比可以看出：在低速时，考虑传动误差的系统模型输出转速波动较大，在波峰处存在0.36 rad的传动误差，平均传动误差0.2 rad，而不考虑传动误差的系统模型在0.2 s后就达到稳定值，之后输出稳定传动误差可以忽略，显然考虑传动误差的系统模型更符合实际情况.在高速时，两种模型则无差别，说明在减速器高速运转时传动误差对系统的影响很小，与低速相比影响可以忽略.后续对CMG框架系统的建模中将采用考虑传动误差的减速器模型，更准确的描述框架系统在低速运转时的输出转速.

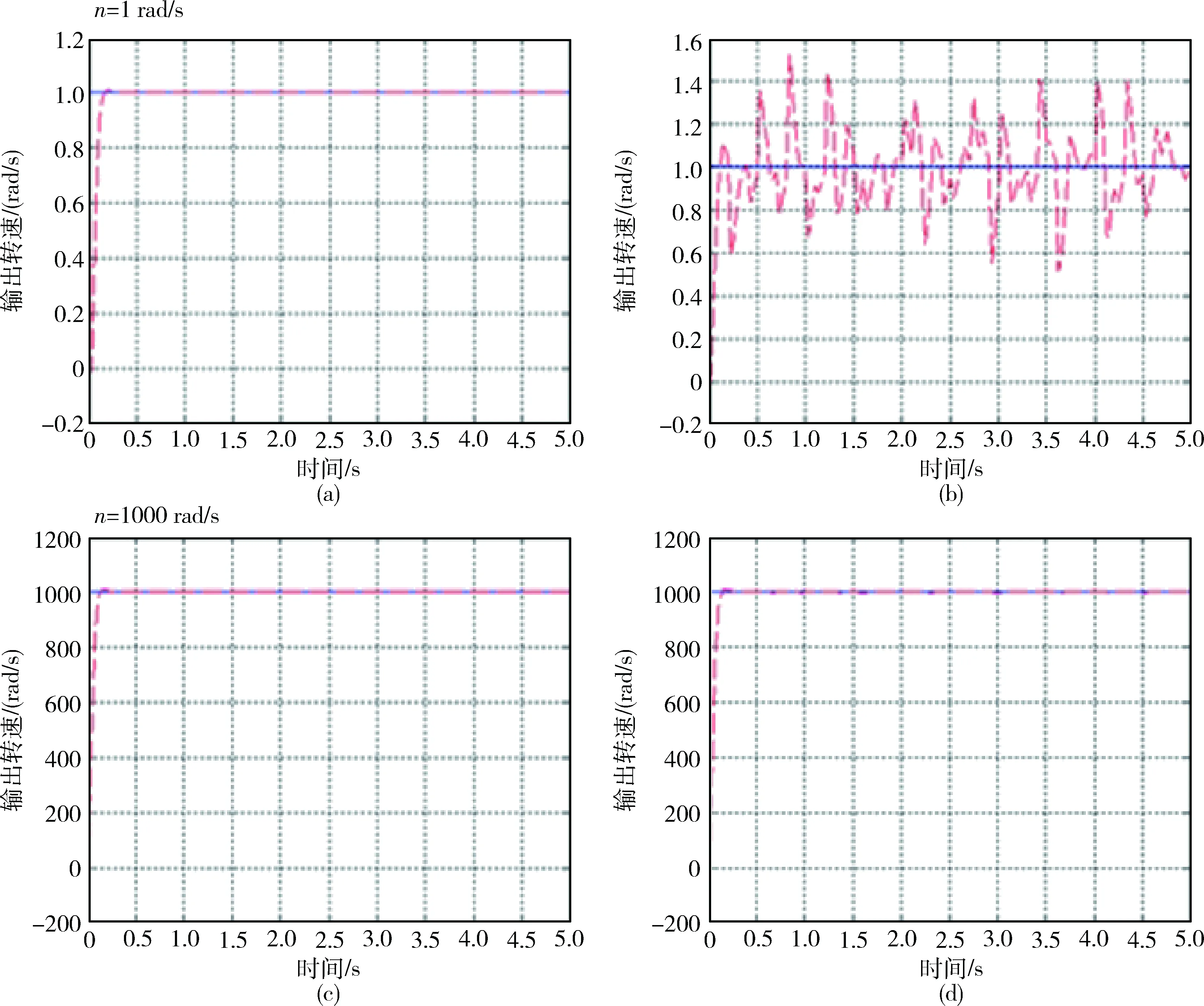
图4　两种减速器模型对比Fig.4　Comparison between two kinds of reducer models

3　控制力矩陀螺框架驱动系统建模

3.1　CMG框架驱动组件结构原理

CMG框架驱动组件结构如图5所示.

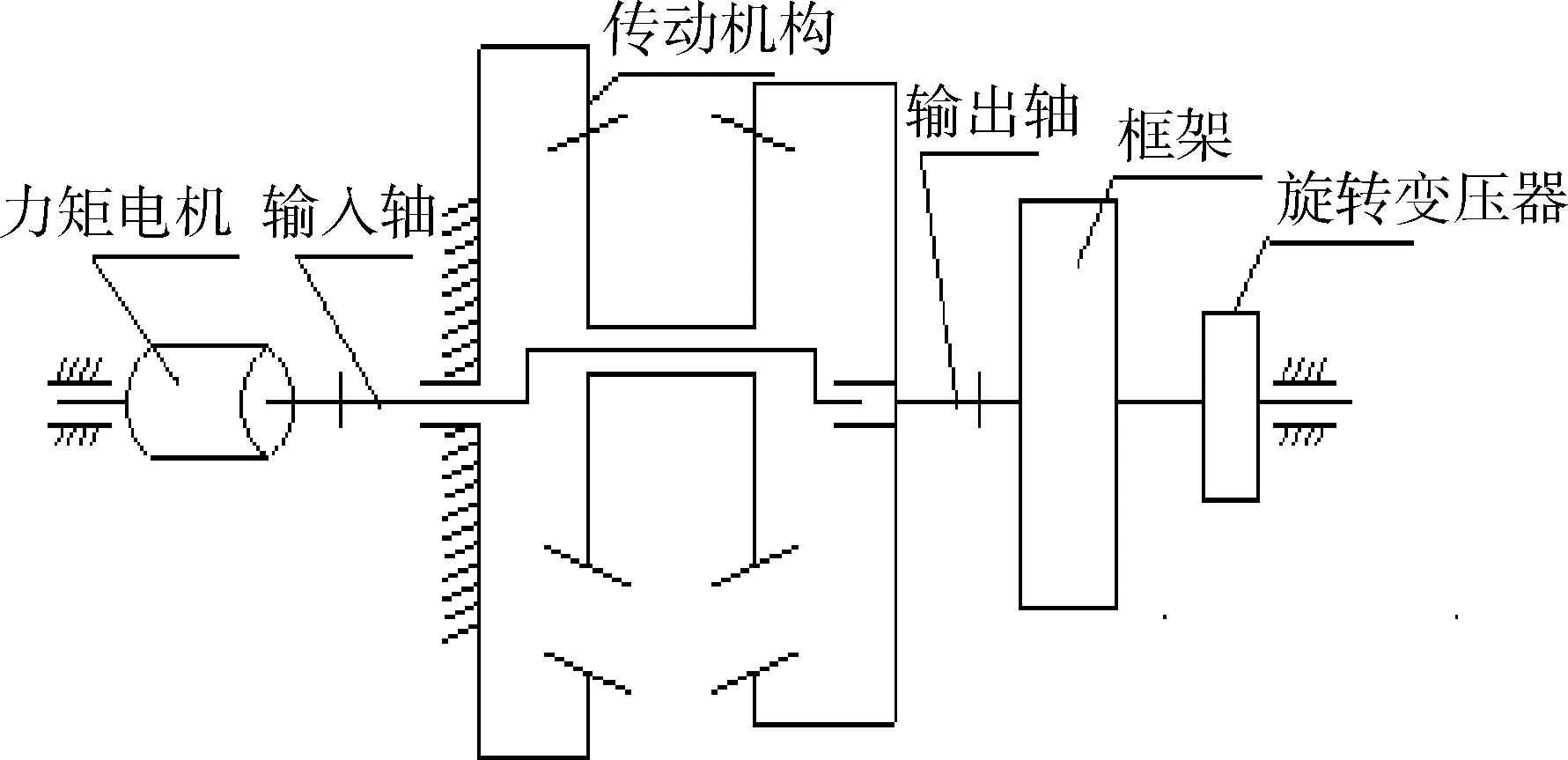
图5　CMG框架驱动组件示意图Fig.5　CMG Gimbal System

CMG框架驱动系统主要由框架电机、谐波减速器、旋转变压器、框架轴承组件等组成.其中，框架电机是驱动框架——转子系统旋转、实现控制力矩陀螺力矩输出的关键组件，框架电机要具有良好的低速稳定性，能将功耗维持较小的水平，研究对象所采用的框架电机为永磁直流无刷电机；谐波减速器的作用是将框架电机的转速以一定的传动比减速并将框架电机的输出力矩放大后驱动框架-转子系统旋转的组件，谐波减速器要具备较大的减速比，而且要求扭转刚度大、反向间隙小、摩擦力矩小等特点；旋转变压器是用于测量框架轴的角位置；框架轴承组件的作用是与供电端轴承组件一起支承框架—转子系统，使其得以旋转.

3.2　CMG框架系统设计

根据图5所示CMG框架驱动组件的结构原理，可以得到框架伺服系统动态电机数学模型：

以我院2017年2月-2018年2月内收治的20例冷凝集素增高患者为实验研究对象,所有患者均存在血型鉴定和交叉配血不合问题,包括9例慢性肺心病患者、6例感染性心内膜炎患者、5例肾病综合征患者。20例患者中男性12人,女性8人,患者年龄18.5-84.3岁,平均(49.6±7.4)岁。

(6)

其中，R为电机绕组电阻，im为电机绕组电流，L为电机绕组电感，Ce为电机反电动势系数，Cl为电机力矩系数.

将式(6)与(1)、(2)联立即为采用谐波减速器的框架伺服系统的数学模型.

在MATLAB/Simulink软件中搭建电机模型，将之前建立好的考虑传动误差的谐波减速器模型封装作为减速器模块，建立完整的CMG框架驱动系统模型.

仿真所采用的CMG框架转速控制系统是是一个转速、位置、电流三闭环控制系统，采用从内环到外环的设计方法，其结构简图如图6所示.

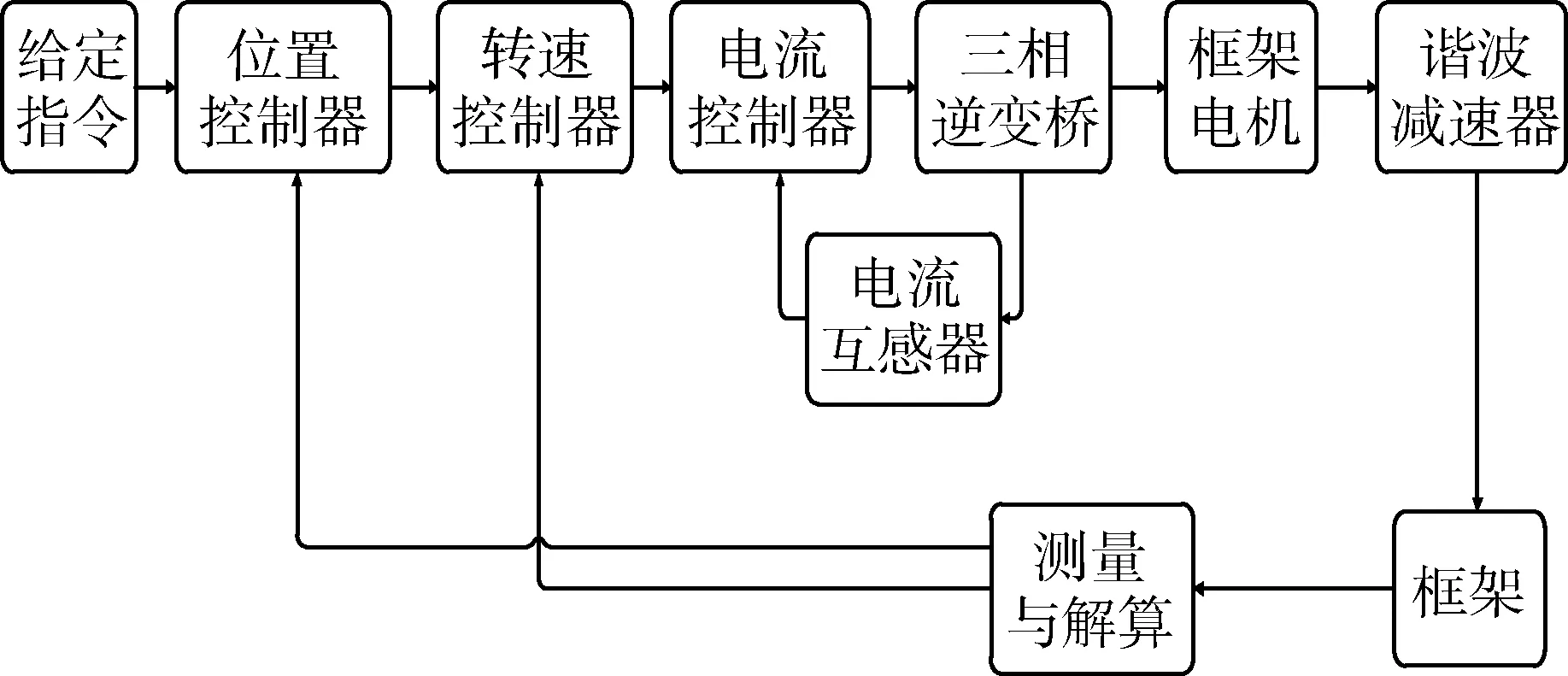
图6　CMG框架转速控制系统Fig.6　Control diagram of CMG gimbal system

4　仿真结果

4.1　CMG框架驱动系统仿真

本文仿真主要数据如表2所示.

表2　CMG框架驱动组件仿真参数Tab.2　Parameters of CMG gimbal system

因减速器存在着i=100的减速比，为模拟框架在低速时的转速，设置电机输出端转速为10 rad/s，则通过减速器的理想输出转速为0.1 rad/s，此时CMG框架输出转速开环仿真曲线如图7所示.

加入PID闭环控制后转速输出曲线如图8所示.输出转速误差降低了53.33%，得到了较好的抑制.

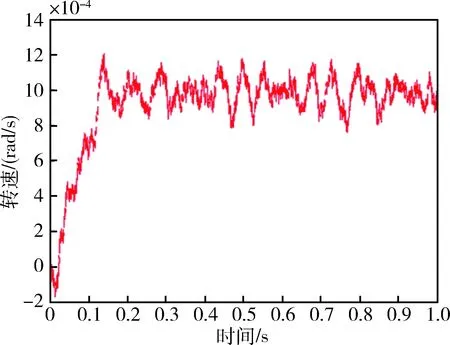
图7　框架输出转速Fig.7　Output velocity of CMG gimbal system

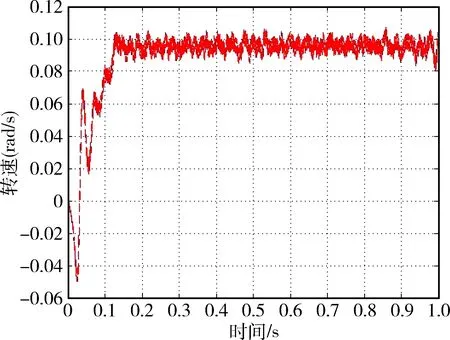
图8　加入PID控制后输出转速Fig.8　Output velocity of CMG gimbal system with PID control

4.2　谐波减速器刚度对框架驱动系统性能的影响

由已建立的CMG框架驱动系统模型研究刚度对框架驱动系统性能的影响，在低转速下(电机输出转速n=10 rad/s)，分别设置刚度为k=2 000 N·m/rad,k=5 000 N·m/rad,k=10 000 N·m/rad,k=20 000 N·m/rad, 可以得到系统在不同刚度条件下的输出转速曲线，如图9所示.

由图9可以看出，随着刚度的增加，输出转速曲线达到稳定值的时间从刚度为2 000 N·m/rad时的0.6 s减小到刚度为20 000 N·m/rad时的0.2 s，输出曲线的误差从2 000 N·m/rad时的5.3%降低到刚度为20 000 N·m/rad时的3.1%.由此可以看出框架驱动组件选用刚度值较大的谐波减速器，可以使输出转速更稳定，精度更高.而在实际情况时，由于谐波减速器的特性，其刚度并不是一个恒定的值，低速时刚度较小，随着速度的增加刚度会随之增加，所以会出现在低速时框架伺服系统输出转速误差较大的现象.

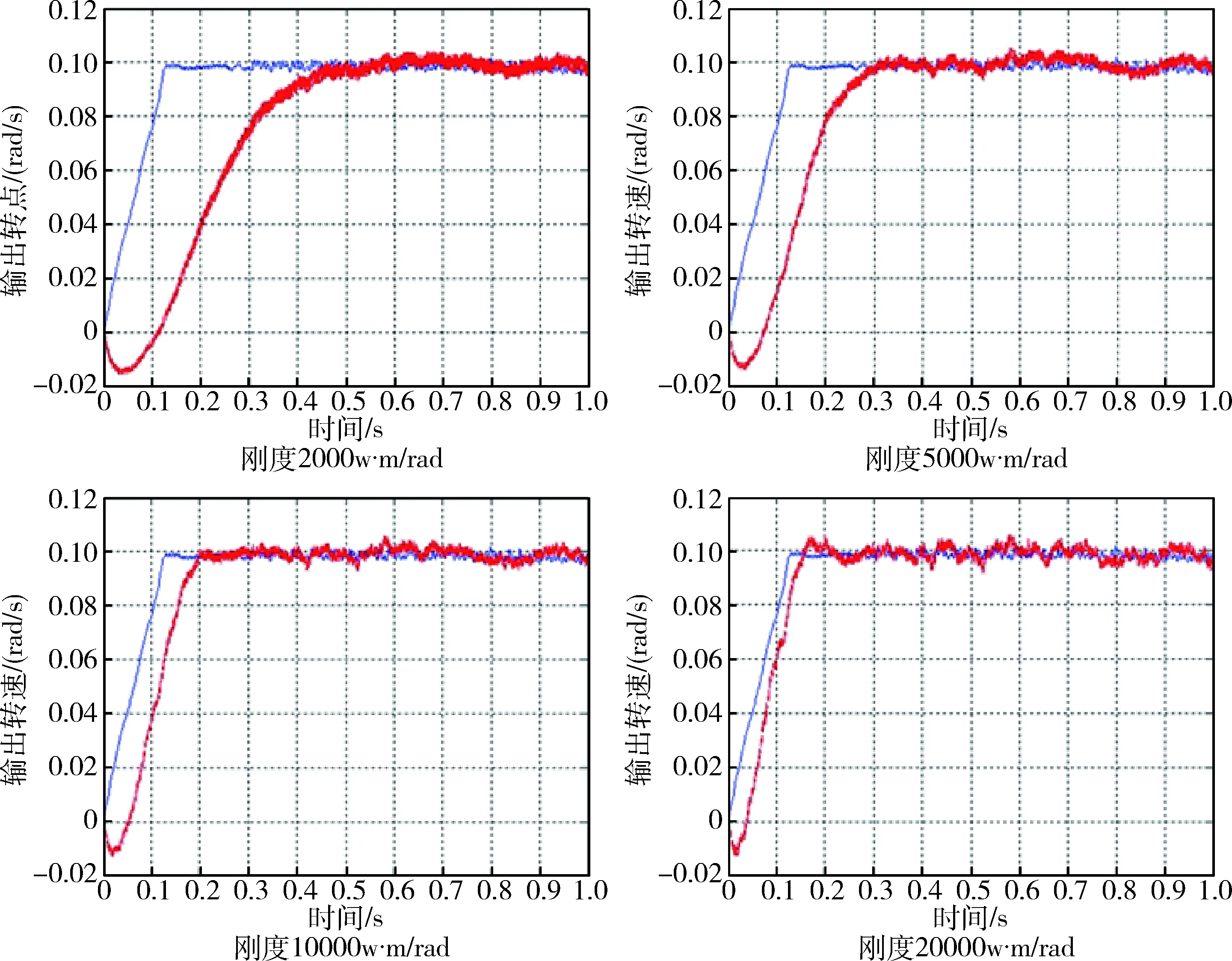
图9　刚度对系统的影响Fig.9　Influence of stiffness on the system

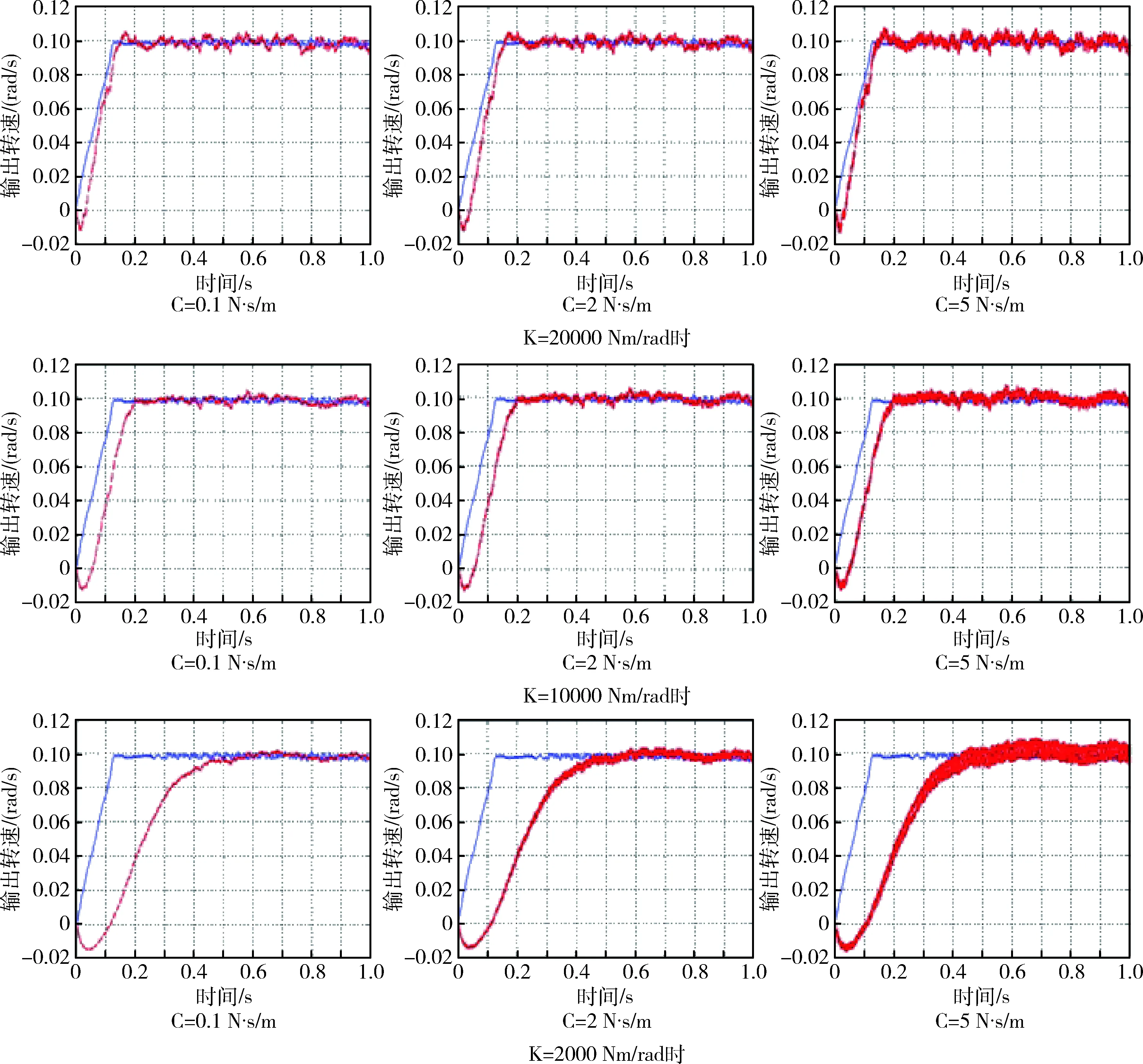
图10　阻尼对系统的影响Fig.10　Influence of damping on the system

4.3　谐波减速器阻尼对框架驱动系统性能的影响

由已建立的CMG框架驱动系统模型可以研究阻尼对框架驱动系统性能的影响，在低转速下(取电机输出转速n=10 rad/s)，设置刚度为k=2 000 N·m/rad,k=10 000 N·m/rad,k=20 000 N·m/rad 3种情况，分别取阻尼c=0.1 N·s/m,c=2 N·s/m,c=5 N·s/m,可以得到系统在不同刚度情况下、取不同阻尼值时系统的输出转速曲线，如图10所示.

从图10可以看出，在谐波减速器刚度很大时，其阻尼对系统的影响可以忽略不计；随着刚度的减小，阻尼对系统的影响逐渐增加；与此同时，在刚度为2 000 N·m/rad时，阻尼取0.1 N·s/m时误差为2.3%，阻尼取5 N·s/m时误差为5.3%，阻尼取5 N·s/m时误差为8.7%，可以看出，随着谐波减速器阻尼的增大，框架系统达到稳定后的误差也会增加.

5　结　论

本文利用MATLAB/Simulink软件建立了综合考虑减速器齿隙、传动误差、刚度、阻尼等因素的CMG框架伺服系统模型.采用PID闭环控制对低速下输出转速误差进行抑制，使输出转速误差降低了53.33%.最后利用模型分析了谐波减速器刚度和阻尼对系统的影响：谐波减速器刚度高时输出转速更稳定、精度更高；在刚度很大时，阻尼对系统的影响可以忽略，随着刚度的降低，阻尼越大系统达到稳定后的误差越大.