基于MATLAB的优化双圆弧插补高次曲线的算法*

王霞琴，张伟华，王发生

(1.兰州石化职业技术学院 机械工程学院，甘肃 兰州　730060；2. 甘肃驰奈生物能源系统有限公司，甘肃 兰州　730050)

0　引　言

工业技术的发展和消费理念的转变促进了曲线形产品的流行。表面圆滑、线条流畅的物体形态除了有较好的使用性能，同时也赋予产品以时代感，在工业生产方面，曲线形模压产品更有便于脱模成形的特点。因而，曲线元素被大量应用于产品当中。然而，产品或模具外形轮廓加工时，所使用到的大多数普通数控加工设备只提供有直线和圆弧插补指令，对于非圆曲线轮廓的加工必须依靠直线段或者圆弧段去拟合逼近非圆曲线。笔者主要针对非圆高次曲线轮廓外形，提出一种优化的双圆弧拟合方法，并运用MATLAB编程语言实现其拟合过程及误差分析，最终生成可加工的数控代码。

1　双圆弧插补的数学模型

在进行产品加工时，刀具轨迹的规划是决定加工效果的重要因素之一。对于非圆曲线的加工，如何生成的有效的加工代码，使之能最接近原曲线，并且任然保持光顺性是加工时要解决的难点问题。针对非圆高次曲线光顺性在加工路径的设计时，考虑用双圆弧插补非圆高次曲线。

1.1　双圆弧样条的做法

在保证曲线拟合的圆弧段能彼此相切的条件下，建立双圆弧样条的数学模型。在双圆弧拟合计算时，为避免复杂的三角运算，而采取矢量计算的方法来求解未知量。

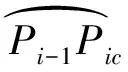
图1　双圆弧样条的做法

双圆弧彼此相切的约束条件有：

1.2　最优切向量的确定

在任意相邻两节点进行双圆弧样条的拟合时，双圆弧的公共单位切向量Ti可以有无穷多个。在进行曲线拟合时，公共单位切向量Ti作为一个自由变量是影响曲线拟合的一个因素。在很多文献中对于在两插值点进行双圆弧拟合时，公共单位切向量Ti的选择大多考虑到拟合圆弧段与圆曲线的相似程度作为目标函数(双圆弧插值曲线曲率的平方沿双圆弧插值曲线的积分值达到最小值)，求取公共切向量。但是在进行非圆高次曲线拟合时，根据高次曲线的曲率是不断发生变化的，并且呈现有明显的加减速度的特点。曲线拟合时，考虑机床刀具运动轨迹的规划，要求运动速度和加速度连续，实现刀具轨迹能够平稳光顺。

因此，在求取公共单位切向量Ti时，要考虑到以下因素：①拟合的双圆弧曲线要平稳、光顺；②双圆弧拟合曲线与原曲线的有较高的相似度。由此，建立新的目标函数：

U=Earc+λEcrv=MIN

式中：Earc为双圆弧样条的曲率差之和，Ecrv为曲率的平方沿曲线的积分值。

由此，可确定满足拟合条件的公共单位切向量Ti。如图1所示，取双圆弧在点取由x轴正方向到Ti-1的转角为φi，由Ti-1到Ti-1的转角为θi。经过大量的计算可知θi≈Δθi/2(其中Δθi为两节点切向量的转角)，为计算简便取定θi=Δθi/2，可以求得：

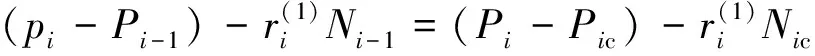
由此，可求得双圆弧的半径和圆心如下：

根据以上公式就可以计算出双圆弧拟合的相关点数据，对曲线进行拟合。

1.3　双圆弧拟合误差的分析

在对高次曲线拟合时，以原曲线和拟合曲线之间的法向距离作为拟合误差的评价标准，来衡量双圆弧样条的拟合效果。若某段曲线的拟合圆弧半径为R，圆心坐标为(xc,yc)，点qi为这段高次曲线上的任意一点，其坐标为(xi,yi)，则在该点处拟合误差为：

在双圆弧样条拟合过程中，影响拟合效果的变量有两个：一是节点的数量，二是双圆弧样条的公共切向量。在最优公共切向量的确定时，为保证拟合效果，切向量计算时已建立目标函数确定其值。

图2　拟合算法流程图

因此，节点数量成为确定拟合误差的唯一变量。拟合曲线是否能达到规定要求，可通过增加节点数量来保证。

2　双圆弧插补高次曲线及程序流程

数控加工非圆高次曲线拟合算法的设计思想如图2所示。将被加工轮廓曲线按曲线加工需要设定一组有序插值点，在每相邻两个插值点之间用双圆弧段拟合，解出所有圆弧段的端点、圆心及半径数据，则预加工曲线能够生成加工程序。生成数控程序之前利用Matlab分析计算拟合误差。一般来说，要获得较好的拟合效果，拟合误差Δ允应控制在零件表面尺寸公差要求的1/5之内[4]。如果拟合误差不能满足设计要求，可以增加节点数量，对曲线重新拟合。根据高次曲线的加工特点，曲率的变化是不均匀的，通过Matlab编程语言设计，对于原曲线节点的选取可根据曲率的变化更改步长，设定节点之间的距离，已获得更好的加工效果。

3　实　验

为检验双圆弧插补法在实际加工中的可靠性，选取涡旋压缩机的核心零件涡旋盘进行数控加工。精加工代码由上述语言编程实现，加工过程如图3所示。加工成品经三坐标测量仪检测，检验结果如表1所示，可知此双圆弧插补法能较好的保证表面加工精度。

图3　涡旋盘的精加工

表1　三维偏差分析结果

4　结　论

在实际加工中，选取一些非圆高次曲线进行加工，在相同的拟合误差下，采用优化双圆弧样条曲线的拟合方法比采用单圆弧或直线段拟合，节点数量少因而程序段减少，加工用时减少，获得了较好的加工效果。同时，结合Matlab计算对组合涡旋型线的拟合过程进行编程，减少了双圆弧样条拟合过程中大量的计算工作量和计算误差，而且编程过程中设计人员可以随时对设计结果进行干预，直接得到数控代码。该算法具有通用性和实用性。也可嵌套在CAD/CAM软件中，实现非圆曲线加工的优化。