基于核密度估计的互联网金融产品收益率对比分析*

马 馨 悦

(南京财经大学 应用数学学院，南京 210023)

从20世纪末开始，互联网信息技术呈现快速发展的势头，也给人们的思维方式和生活方式带来了巨大改变。在金融领域，互联网技术和金融业务的结合产生了一种新型的产品和业务模式——互联网金融。目前互联网金融大致可以分为如下4类：传统金融业务的互联网化、基于互联网平台开展的金融业务、全新的互联网金融模式以及金融支持的互联网化。

由于近几年互联网金融发展风头正劲，大众理财思维已由传统产品转向购买互联网平台的理财产品，其中2013年6月基于支付宝平台的天弘基金余额宝的横空出世，被普遍认为开创了国人互联网理财元年，余额宝也是迄今中国最大的货币资金[1]。同年10月微信理财通旗下的华夏财富宝货币基金应运而生，且发展迅速。余额宝和财富宝均为货币基金，具有低风险，高流动性，1元起投且随买随取的特征，因此成为当下互联网金融投资产品的代表。

学者们对传统金融产品的研究已经有很多，尤其是对金融资产收益率分布的研究。大量的实证研究表明：绝大多数金融资产的收益明显不符合正态分布假定，一般呈现“尖峰厚尾”特征[2]，因此国内外许多学者都进行了股票收益率分布的探索。在已有的国外股指收益率研究里，最早由Kendall[3]通过对英国股票价格的研究发现：股价的变动只是近似地服从正态分布，且大多数价格上的变化存在很明显的尖峰厚尾现象。Mandelbrot[4]认为这种不满足正态分布的现象不是偶然出现的，尖峰与厚尾的特征几乎为所有股票收益率数据所共有。我国也有相关学者证实了金融资产的相关指数或收益率。林美艳等[5]通过Q-Q图和有方向检验检验了1996-01-02到2001-12-28的上证指数日、周、月对数收益率，发现上证指数收益率不服从正态分布，反而是具有尖峰厚尾特征的t分布能够较好地拟合股指收益率数据。张德飞[6]建立股票指数的随机微分方程模型来刻画股票指数的许多统计特征，从而证实股票指数不服从正态分布。徐晓岭等[7]对上证指数收益率提出了一种混合正态分布的估计方法，即假设证券收益率分布函数是两个正态分布凸组合，使用经验分布极大极小准则得到参数的估计值，但没有说明混合正态分布究竟是否较好刻画收益率分布。

近些年，利用非参数估计方法——核密度估计对股票收益率进行拟合取得了显著不错的成果。非参数估计一般不对数据的分布作任何假定，估计的结果更加稳健[8]。在已有传统金融产品研究的基础上，本文使用非参数估计方法中的核密度估计对互联网金融产品——余额宝和财富宝二者收益率进行估计及对比。

1 核密度估计

在统计学中，往往需要根据样本数据去推断总体的分布，即密度函数。如果采用参数估计的方法，则要先假定总体分布的具体形式，如总体服从正态分布N(μ，σ2)，然后利用样本数据去估计参数(μ，σ2)，从而得到总体的密度函数。但若真实总体与假定分布相差甚远，则根据参数估计法得出的统计推断可能具有较大偏差。而非参数估计的方法可以在不假设总体分布的情况下进行密度函数的估计，从而降低误差。

本文选取非参数估计中的核密度估计对余额宝和财富宝收益率进行密度函数估计，其步骤一般如下：先选取核函数，然后计算最优带宽，最后进行核密度估计。

1.1 核函数

核密度估计[9]是由Rosenblatt(1956)和Parzen(1962)对直方图作密度估计的思想推广而来的。利用直方图作密度估计时，即使随机变量是连续的，直方图也始终是不连续的阶梯函数，而核密度估计可以解决这一缺点，从而得到密度函数的光滑估计，其核心是采用一个光滑可微的核函数。核密度估计量为

(1)

其中，函数K(·) 称之为核函数，h称为带宽。式(1)满足以下性质：

(i)K(·)连续且关于原点对称。

(iii)①z0>0 ，|z|≥z0时，K(z)=0；

②当|z|→∞ 时，|z|K(z)→0。

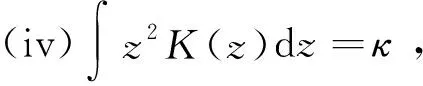
条件(iii)要求核函数的曲线下面积为1(将核函数标准化)，并满足一些有界条件。条件(iii)下①比②更强，在实践中常常采用条件①，即如果超出某个邻域范围[-z0，z0]，权重变为0，常将[-z0，z0]标准化为[-1，1] 。条件(iv)也是一个有界条件。

现给出常见核函数见表1：

表1 常见核函数

其中，均匀核也用于直方图，只是在用均匀核进行核密度估计时并不固定分组，而在每个点上进行估计，最流行的核函数为二次核与高斯核。条件(iii)下除高斯核满足②外，表1中的其他核均满足①。这些核函数的共同特点是，离原点越近，核函数的取值越大，并在原点处取得最大值，这意味着，越近的点给与的权重越大。

1.2 最优带宽

(2)

其中，

则式(2)可以改写成

均方误差依赖于每一个观测值，若希望对x所有取值的均方误差进行整体度量，则可以最小化积分均方误差(IMSE)：

为求解minIMSE (h)，Silverman(1986)[10]证明最优带宽为

(3)

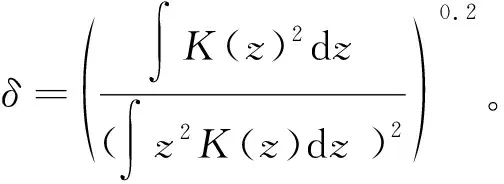
从式(3)可以看出，最优带宽h*依赖于δ从而依赖于核函数，还依赖于待估密度函数的二阶导数f″(x) 。对于不同的核函数分别使用不同的δ。

若样本来自于正态总体，则可以计算出h*=1.364 3δN-0.2s，其中s为样本标准差。为了防止样本标准差受极端值的影响，常使用Silverman嵌入估计，可得h*=1.364 3δN-0.2min(s，iqr/1.349) 其中，iqr为样本的四分位距。

在实际操作中，即使整体不服从正态分布，也可以使用嵌入估计来进行带宽的选择，但为了保险起见，可以比较两倍嵌入估计与一半嵌入估计的效果[11]。

2 余额宝和财富宝收益率差异比较

2.1 数据说明

本文选取余额宝和财富宝的7日年化收益率作为对比数据，7日年化收益率是指货币基金最近7日的平均收益水平，进行年化以后得出的数据[12]。考虑到两个基金在发布后需要一段时间的市场适应，选取2014-03-01至2017-10-20的收益率数据进行对比。将余额宝和财富宝收益率分别表示为样本x，y，单样本容量为1 330，总样本容量为2 660。数据来源天天基金网，分析软件选取R。

2.2 数据基本统计特征及正态性检验

首先，作出余额宝和财富宝的收益率的趋势变动图，见图1。可以发现二者收益率均具有很大的变动。

其次，对样本x，样本y的一些基本数字特征进行描述，对样本进行ADF平稳性检验。将基本特征及ADF检验对应的p值一起记录在表2。

从表2中可以发现，样本x的均值和标准差均小于样本y，说明余额宝的收益率略低于财富宝，但波动性较小。两样本的偏度均大于0，表明两组收益率分布均右偏，峰度分均小于3，说明二者分布均呈现平顶峰。

样本x进行ADF检验对应的p值为0.863 3，大于0.05，样本y进行ADF检验对应的p值为0.019 3，小于0.05，说明在0.05的显著性水平下，余额宝收益率不平稳，财富宝收益率平稳。

图1 余额宝及财富宝收益率的时序图

观察数据是否为正态分布，最直观的方法就是画Q-Q图(分位数-分位数图)，即将正态分布的分位数与样本数据的分位数化成散点图，若样本服从正态分布，则图中散点应该集中在45°线附近[13]。将余额宝、财富宝收益率的数据进行正态性检验，得到Q-Q图见图2。可以看出，两个样本的尾部均明显偏离直线，意味着两个样本均不服从正态分布。也说明，用核密度估计对余额宝和财富宝的收益率进行研究具有意义。

(a)余额宝 (b)财富宝

图2余额宝和财富宝的收益率正态性检验Q-Q图

Fig.2Q-QdiagramofnormalyieldofYu’EBao&Cai’FuBao

2.3 核密度估计及分析

在进行核密度估计之前，先做出余额宝及财富宝的收益率频数分布直方图，见图3。可以看出二者收益率都是在[0.04，0.045]区间内的频率最大，说明两者收益率大都集中在该区间内。但余额宝落在该区间内的频数大于400，而财富宝对应频数略高于300，说明余额宝有更大的概率收益率稳定在该区间内。对于余额宝来说，其落在[0.02，0.025]区间内的概率位居第二，而财富宝频率第二大区间则为[0.025，0.03]，明显高于余额宝。

(a)余额宝 (b)财富宝

图3余额宝和财富宝的收益率频数直方图

Fig.3ThefrequencydistributionmapoftheincomerateofYu’EBao&Cai’Fu

将两组数据得到的最优窗宽及两倍、一半的窗宽带入进行核密度估计，结果见图4。可以看出，两种收益率均为选取嵌入估计得到的最优带宽一半时进行核密度估计更光滑。余额宝和财富宝收益率均呈现双峰分布，说明二者收益率集中在两个值附近，一个是较低的收益率，一个是较高的收益率，从而说明余额宝和财富宝的收益率并不是一直稳定的。通过观察二者的收益率原始数据对应的时间节点发现，二者收益率均从较大的逐步降到较小。

(a)余额宝 (b)财富宝

图4带宽选择的核密度估计图

Fig.4Kerneldensityestimationofbandwidthselection

图5 核密度估计结果对比

现将两组收益率的核密度估计进行对比，结果见图5。由图5可以看出，余额宝的收益率对应概率密度曲线要尖，说明其分布在某点处的可能性更大，余额宝更易长期稳定在某一收益率附近。同时，财富宝收益率跨度更大，说明虽然其密度估计的结果较好，但会出现较高或者较低等极端值的情况。

结合图3，余额宝的峰值一个在0.023左右，另一个在0.043左右。财富宝的峰值一个在0.029，一个在0.045左右，且财富宝收益率的核密度估计曲线基本一直在余额宝收益率估计曲线的右侧，说明财富宝的收益率普遍比余额宝的收益率高。

3 结论及意义

无论是均值还是核密度估计图均能看出，微信理财通平台财富宝收益率比支付宝平台的余额宝收益率要高。因此对于用户的个人理财，单从收益一方面来看，选择财富宝要获得更高的收益。

但金融市场中，一个理性的经济人往往考虑的不止收益率一方面，还注重于风险的控制。风险控制模型中较为常用的是 VaR模型，此模型可以对风险价值进行计算。传统上会假定收益率或者对数收益率服从正态分布[14]。然而大量文献研究表明收益率并不服从正态分布，而是呈现尖峰后尾的分布。因此在进行VaR风险度量时，正确估计出收益率的分布可以令风险模型更加准确，得到的结果也更具说服力。

条件异方差作为一种动态非线性的股权定价模型[15]，研究者通常假定对该模型的资产收益服从正态分布，再利用最小二乘估计、极大似然估计、广义矩估计等方法来估计ARCH模型、GARCH模型中的参数。而这种正态的假定若与实际分布不相同，参数估计过程中会出现很大的偏差。本文采用非参数方法中的核密度估计对余额宝及理财宝收益率进行密度估计，不仅对传统金融市场中的模型具有参考意义，也能为新型互联网金融市场研究提供参考。

参考文献(References)：

[1] 庄雷. 余额宝与国债市场收益率波动的实证研究[J].经济与管理，2015(3)：74-79

ZHUANG L. An Empirical Study of Yu E Bao and Treasury Market Returns Volatility[J]. Economy and Management，2015(3)：74-79

[2] 杨一文，刘贵忠.分形市场假说在沪深股票市场中的实证研究[J].当代经济科学，2002(1)：75-79

YANG Y W， LIU G Z. Empirical Analysis on Fractal Market Hypothesis in Shanghai and Shenzhen Stock Markets[J]. Modern Economic Science， 2002(1)：75-79

[3] KENDALL M G，BRADFORD H A. The Analysis of Economic Time-Series-Part I： Prices[J].Journal of the Royal Statistical Society，Series A (General)， 1953，15(6)：11-34

[4] MANDELBROT B， TAYLOR H M. On the Distribution of Stock Price Difference[J]. Oper Res，1967：1057-1062

[5] 林美艳，薛宏刚，赵凤群，等.上证综合指数收益率的统计分析[J].运筹与管理，2005，14(2)：115-119

LIN M Y，XUE H G，ZHAO F Q，et al.Statistical Analysis on the Yield of Shanghai Composite Index[J]. Operations Research and Management Science，2005，14(2)：115-119

[6] 张德飞，段星德.随机微分方程的非参数估计及其在股票指数中的应用[J].重庆工商大学学报(自然科学版)，2009，26(5)：429-433

ZHANG D F，DUAN X D. Non-parametric Estimation of Stochastic Differential Equations and Its Empirical Study on Stock Index[J]. Journal of Chongqing Technology and Business University(Natural Science Edition)， 2009，26(5)：429-433

[7] 徐晓岭，放嵩，顾蓓青.上海股票市场收益率分布研究[J].数学理论与应用，2010， 30(3)：28-31

XU X L， FANG S，GU B Q. Study on the Distribution of Yield in Shanghai Stock Market[J]. Mathematical Theory and Applications， 20010， 30(3)：28-31

[8] 解其昌.稳健非参数VaR建模及风险量化研究[J].中国管理科学，2015，23(8)：29-38

XIE Q C.Robust Nonparametric VaR Modeling and Risk Quantification Research[J]. Chinese Journal of Management Science，2015，23(8)：29-38

[9] KEELE L. Semiparametric Regression for the Social Sciences [M]. John Wiley and Sons， 2008

[10] SILVERMAN B W. Density Estimation for Statistics and Data Analysis[J]. Chapman & Hall， London， 1986(39)：296-297

[11] 陈强.高级计量经济学及Stata应用[M].北京：高等教育出版社， 2014

CHEN Q. Advanced Econometrics and Stata Application[M].Beijing：Higher Education Press，2014

[12] 罗强强，吴洁，吴承逊.互联网金融理财产品——余额宝的收益与风险研究[J].现代商业，2015(28)：20-21

LUO Q Q， WU J， WU C X. Internet Financial Products——the Balance of Treasure Income and Risk [J]. Modern Commerce， 2015(28)：20-21

[13] 刘红忠，何文忠.股票收益率分布的核密度估计及蒙特卡罗模拟检验——基于涨跌停板制度推出前后数据的比较研究[J].世界经济文汇，2010(2)：46-55

LIU H Z， HE W Z. Simulation Test：A Comparative Study Based on the Data of Price Limits Before and After the Introduction of Kernel Density Estimation and Monte Carlo Distribution of Stock Returns[J]. World Economic Papers， 2010(2)：46-55

[14] 吴慧慧.人民币汇率厚尾特征及VAR估计[J].重庆工商大学学报(自然科学版)，2017，34(2)：41-47

WU H H. The Thick Tail Characteristics of RMB Exchange Rate and VAR Estimation[J]. Journal of Chongqing Technology and Business University (Natural Science Edition)， 2017，34(2)： 41-47

[15] 王燕.时间序列分析—基于R [M].北京：中国人民大学出版社，2015

WANG Y. Time Series Analysis：Based on R[M]. Beijing：China Renmin University Press，2015