分数阶混沌系统的间歇控制同步*
2018-07-10王娴,李东
王 娴, 李 东
(重庆大学 数学与统计学院,重庆 401331)
0 引 言
近年来的研究发现大部分整数阶混沌系统的阶数调整为分数阶时,系统仍具有混沌行为,且能更好地描述各类复杂力学和物理行为,如分数阶Lorenz系统[1]、分数阶Chua系统[2]、分数阶Liu系统[3]、分数阶Lü系统[4]等。
纵观已有的分数阶混沌控制同步方案,绝大多数都是建立在连续控制基础之上的。如主动滑膜控制法、反馈控制法、模糊控制法、自适应法[5]、脉冲同步[6]等。而间歇控制同步是一种较为重要的不连续同步方法,与脉冲同步有着一定的相似性。间歇控制可根据控制器是否工作将每个时间段分为“工作时间”和“休息时间”。当工作时间趋于一个点时,间歇控制就变成了脉冲控制;而当休息时间趋于零时,间歇控制就变成了连续控制。因此间歇控制同步方法更具有研究意义。目前,间歇控制在整数阶混沌系统中已取得了一定的成果,文献[7]首次提出了一种新的混沌控制方法—间歇控制法,并从理论上验证了方法的可行性。文献[8]详细讨论了间歇反馈对时滞混沌系统的控制问题,数值模拟验证了方法的有效性。在文献[9]将间歇方法应用于时延复杂网络系统,是间歇控制方法向实际应用的推广。但由于分数阶混沌系统的复杂性,间歇控制同步在分数阶混沌系统及在实际中的应用还需要去完善。
通过对分数阶混沌系统间歇控制同步的研究,基于Lyapunov稳定性理论构造合适的控制器得到其间歇控制同步稳定性的判定,并依此判定对分数阶混沌系统进行间歇控制同步研究。运用Matlab软件绘制分数阶Chen混沌系统的状态图和相图,以及同步误差系统的状态图,以验证方法的可行性和有效性。
1 问题的描述和系统模型
分数阶微分有多种定义方式,采用Riemann-Liouville(R-L)分数阶微分[10]定义如下:
(1)
其中q为分数阶阶次,Γ(·)为伽马函数。
考虑如下分数阶混沌系统
Dαx(t)=Ax(t)+φ(x(t))
(2)
其中x(t)=(x1(t),x2(t),…,xn(t))T∈Rn是系统的状态变量,α=(α1,α2,…αn)T,0<αi<1,i=1,2,…,n;A∈Rn×n是线性部分的系数矩阵,φ(x(t)):R+×Rn为非线性项。
为研究分数阶混沌系统同步问题,可将系统式(2)作为驱动系统,并选择如下形式的响应系统:
Dαy(t)=Ay(t)+φ(y(t))+u(t)
(3)
其中u(t)为间歇控制器,控制器的设计如下:
(4)
其中{τm},m=0,1,2…为一列时间点。
定义同步误差为e(t)=y(t)-x(t),则误差系统可描述为
Dαe(t)=Ae(t)+φ(y(t))-φ(x(t))+u(t)
(5)
可通过研究误差系统式(5)的渐近稳定性来实现系统式(2)和系统式(3)的同步。由于分数阶微分方程稳定性理论的发展不成熟,为解决问题,通过构造一个新的间歇可控响应系统,将分数阶间歇系统转化为整数阶间歇系统。
构造整数阶系统如下:

(6)
于是得到整数阶误差系统为
(7)
要实现驱动系统式(2)和响应系统式(3)的间歇同步,只需在整个时间区间满足误差系统式(7)的状态变量最终趋于零。
即
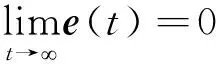
为得到误差系统式(7)的稳定性条件,需要如下假设。
假设1 假设φ(x)是Lipschitz连续函数,即存在一个正常数L,对∀x1,x2∈Rn,下式成立:
‖φ(x1)-φ(x2)‖≤L‖x1-x2‖
(8)
2 主要结论
给出一个渐近稳定的判据并提供严格的数学证明过程。
定理1 如果存在一个正定、对称的矩阵P和正常数θ1,θ2,使得
(a)ATP+PA+KTP+PK+2LP+θ1P<0;
(b)ATP+PA+2LP-θ2P<0;
(c) 对任意的m∈N,存在一个相应正常数ηm>1,使得ηmexp(-θ1(τ2m+1-t2m)+θ2(τ2m+2-τ2m+1))<1,则系统式(7)渐近稳定,系统式(2)和系统式(3)达到同步。
证明: 考虑如下的Lyapunov函数
V(t)=eT(t)Pe(t)
(9)
当t∈[τ2m,τ2m+1)时,根据假设1及定理1中条件(a)可得

eT(t)(ATP+KTP)e(t)+(φ(y(t))-
φ(x(t)))TPe(t)+eT(t)(PA+PK)e(t)+
eT(t)P(φ(y(t))-φ(x(t)))≤eT(t)
(ATP+KTP+PA+PK)e(t)+
2LeT(t)Pe(t)=eT(t)(ATP+KTP+
PA+PK+2LP+θ1P)e(t)-
θ1V(t)≤-θ1V(t)
(10)
即当t∈[τ2m,τ2m+1)时,
V(t)≤V(t2m)exp(-θ1(t-t2m))
(11)
当t∈[τ2m+1,τ2m+2时利用假设及定理1中条件(b)可得:

eT(t)(ATP)e(t)+(φ(y(t))-
φ(x(t)))TPe(t)+eT(t)(PA)e(t)+
eT(t)P(φ(y(t))-φ(x(t)))≤eT(t)
(ATP+PA)e(t)+2LeT(t)Pe(t)=
eT(t)(ATP+PA+2LP-
θ2P)e(t)+θ2V(t)≤θ2V(t)
(12)
即当t∈[τ2m+1,τ2m+2)时有
V(t)≤V(t2m+1)exp(θ2(t-t2m+1))
(13)
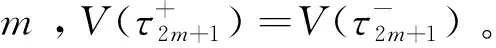
当m=0时,即t∈[t0,t1),由式(12)可知
V(t)≤V(t0)exp(-θ1(t-t0))
(14)
当t∈[t1,t2)时,根据式(13)可知
V(t)≤V(t1)exp(θ2(t-t1))≤
V(t0)exp(-θ1(t1-t0))exp(θ2(t-t1))
(15)
以此类推,可得当t∈[t2m,t2m+1)时,有
V(t)≤V(t2m)exp(-θ1(t-t2m))≤V(t0)exp(-θ1(t1-t0))exp(θ2(t2-t1))exp(-θ1(t3-t2))exp(θ2(t4-t3))…exp(-θ1(t2m-1-t2m-2))exp(θ2(t2m-t2m-1))exp(-θ1(t-
(16)
由定理1的条件(c)对任意i存在ηi>1,使得
(17)
可得
(18)
其中V(t0)为初值且有界,θ1为正数,exp(-θ1(t-t2m))为有界值,则t→时,m→,从而V(t)→0。
当t∈[t2m+1,t2m+2)时,有
(V(t)≤V(t2m+1)exp(θ2(t-t2m+1))≤V(t0)exp(-
(19)
由定理1的条件(c),对任意i存在ηi>1,使得
(20)
可得
t2m))exp(θ2(t-t2m+1))
(21)
其中V(t0)为初值且有界,θ1,θ2皆为正数,exp(-θ1(t2m+1-t2m))和exp(θ2(t-t2m+1))为有界,则t→时,m→,V(t)→0。所以误差系统式(7)是渐近稳定的。即系统式(2)和式(3)达到同步,证毕。
实际应用中采用间歇控制器实用性与可操作性更好,因此将上述定理中间歇控制器u(t)设计为周期间歇控制器
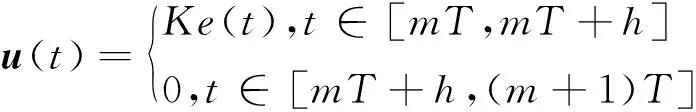
(22)
其中m=0,1,2…,T为周期,h 推论1 在假设1成立的条件下,设计满足式(22)的周期间歇控制器u(t),如果存在一个正定、对称的矩阵P和正常数θ1,θ2,使得 (a)ATP+PA+KTP+PK+2LP+θ1P<0; (b)ATP+PA+2LP-θ2P<0; (c)θ1h+θ2h-T>0。 那么系统式(7)渐近稳定,系统式(2)和式(3)达到同步。 选择分数阶Chen系统作为驱动系统: (23) 当参数取值为(α1,α2,α3)=(0.9,0.95,0.95)和(a,b,c)=(35,3,27)时,系统式(23)存在混沌吸引子,其混沌相图如图1所示。 图1 分数阶Chen系统的相图 设响应系统如下: (24) 系统参数同式(23)。无控制条件下系统式(23)和系统式(24),其误差曲线见图2。 图2 无控制时的系统误差曲线图 根据系统的参数设置,可得 图3 间歇控制时的系统误差曲线图 从图3可以看出,系统在周期间歇控制下,误差系统是渐近稳定的,驱动系统式(23)和响应系统式(24)达到同步。 针对分数阶混沌系统同步问题进行了研究,通过设计间歇控制器,实现了对分数阶混沌系统的不连续控制,由于分数阶微分方程稳定性理论的发展不成熟,通过对控制器的改进将分数阶同步误差系统转化为整数阶同步误差系统,基于Lyapunov稳定性理论,再利用整数阶间歇系统的稳定性判定,得出分数阶混沌系统间歇控制同步理论。数值模拟验证了理论的有效性和可行性。 参考文献(References): [1] HUANG L, FENG R, MAO W. Synchronization of Chaotic Systems Via Nonlinear Control[J]. Physics Letters A, 2004, 32(4): 271-275 [2] ZHU H, ZHOU S, ZHANG J. Chaos and Synchronization of the Fractional Order Chua,s System[J]. Chaos Solitons & Fractals, 2009, 39(4): 1595-1603 [3] 陈向荣,刘崇新,王发强. 分数阶Liu混沌系统及其电路实验的研究与控制[J]. 物理学报,2008, 57(3): 1416-1422 CHEN X R, LIU C X, WANG F Q,et al. Study on the Fractional Order Liu Chaotic System with Circuit Experiment and Its Control[J]. Acta Physica Sinica, 2008, 57(3): 1416-1422 [4] LU J G. Chaotic Dynamics of the Fractional Order Lü System and Its Synchronization[J]. Chinese Physics. 2006, 59(2): 301-305 [5] 胡玉婷,李东,张兴鹏. 参数未知的分数阶混沌系统的自适应追踪控制[J]. 重庆工商大学学报(自然科学版),2015,32(3): 1-7 HU Y T, LI D, ZHANG X P. Adaptive Tracking Control of Fractional Order Chaotic Systems with Unknown Parameters[J]. Journal of Chongqing Technology and Business University (Natural Science Edition) , 2015, 32(3): 1-7 [6] 马铁东,江伟波,浮洁. 基于比较系统方法的分数阶混沌系统脉冲同步控制[J]. 物理学报,2012,61(9):39-44 MA T D, JIANG W B, FU J. Impulsive Synchronization of Fractional Order Hyperchaotic Systems Based on Comparison System[J]. Acta Physica Sinica, 2012, 61(9):39-44 [8] LI C, LIAO X, HUANG T. Exponential Stabilization of Chaotic Systems with Delay by Periodically Intermittent Control[J]. Chaos an Interdisciplinary Journal of Nonlinear Science,2007,17(1): 431-438 [9] 孙海义,李宁,张庆灵. 时延复杂网络的自适应周期间歇同步控制[J]. 控制与决策,2013(5): 797-800 SUN H Y, LI N, ZHANG Q L. Synchronization of Delayed Complex Dynamical Networks Via Adaptive Periodically Intermittent Control[J]. Control and Decision, 2013(5): 797-800 [10] ERTURK V S, MOMANI S, ODIBAT Z. Application of Generalized Differential Transform Method to Multi-order Fractional Differential Equations[J]. Communications in Nonlinear Science & Numerical Simulation,2008,13(8): 1642-16543 数值仿真



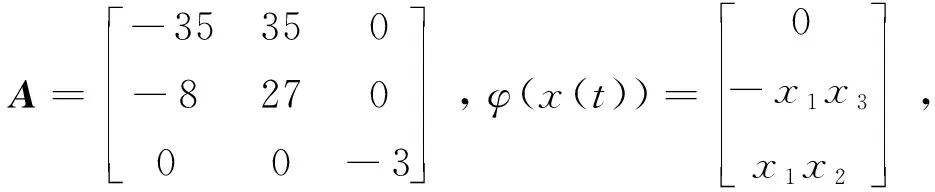


4 结 论
