广义变系数Hirota-Satsuma方程组的等价变换和守恒定律*

程爱芳， 陆 斌

(安徽大学 数学科学学院，合肥 230601)

0 引 言

Hirota-Satsuma方程或耦合Korteweg-de Varies方程的形式是：

(1)

方程组式(1)在1981年由Hirota和Satsuma首次提出，用来描述有不同色散关系的两个长波的相互作用。关于方程组式(1)，已经做了大量的研究。变系数非线性偏微分方程可以被用来描述一些复杂的现象，因此主要研究广义变系数Hirota-Satsuma方程组：

(2)

其中，pi(t)(i=1，2，3)，α(t)和β(t)是关于t的解析函数。当p1(t)=3，p2(t)=-6，方程组式(2)可以转化成方程组式(1)。

1 等价变换

主要研究了方程组式(2)的等价变换。方程组式(2)的等价变换是增广空间(t，x，u，v，α，β，p1，p2，p3)上一个非退化点变换。应用微分方程李不变性准则[1]求解方程组式(2)的等价变换。在无穷小准则下，要求延拓方程组不变，其方程组为

ut-p1(t)uux-p2(t)vvx-α(t)uxxx=0

vt-p3(t)uvx-β(t)vxxx=0

(3)

考虑增广空间(t，x，u，v，α，β，p1，p2，p3)上无穷小生成元的单参数群的等价变换：

连续性等价变换群的生成元的形式是：

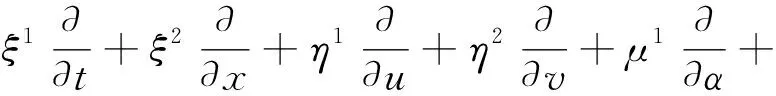
(4)

通过在延拓方程组上应用无穷小生成元的三阶延拓，可以得到关于ξ1，ξ2，η1，η2，μ1，μ2，μ3，μ4和μ5的多因素决定的线性微分方程组，通过求解这个方程组，可知方程组式(2)的等价代数Lε是4维李代数，且有下列一组基：

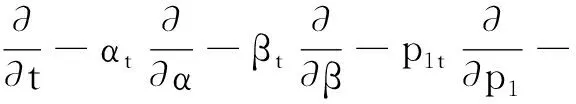
(5)

2 偏微分方程的李对称分析

广义Hirota-Satsuma方程组的对称群由下列形式的向量生成：

(6)

通过经典的李群方法[2，3-5]，在方程组式(2)中应用三阶延拓，可以得到一个关于ξt，ξx，ηu和ηv多因素决定的线性微分方程组。求解这个微分方程组，得到无穷小元素ξt，ξx，ηu和ηv：

ξt=f(t)=

ξx=c1x+c2

ηu=c4u

ηv=c5v

(7)

其中ci(i=1，…，5)是任意的常数，且p3(t)是任意的函数。函数pi(t)(i=1，2)，α(t)和β(t)有下列关系：

p1(t)=k1p3(t)

其中k1是任意的常数。

既然南海问题已经成为某些国家视野中的国际议题，那么中国有必要适时推出中国话语体系下的南海叙事框架，包括历史背景、现状、稳定机制和解决方案等。在这方面，中国历史上的“郑和模式”就是替代和超越上述意象的重要选项之一。

由于式(7)包含5个任意的常数，因此方程组式(2)的无穷小对称形成了五维李代数，由下列线性无关的算子生成：

3 非线性伴随

守恒定律是非线性科学中的一个重要概念，有研究偏微分方程的重要性质，例如数值解法，可积性和线性化，特别是解的存在性，唯一性和稳定性分析。微分方程非线性伴随的性质在参考文献[6-7]中已经说明了能够构造大量不同的守恒定律。

考虑广义变系数Hirota-Satsuma方程组：

(8)

规范的拉格朗日形式为

(9)

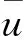
(10)

其中

而Dt和Dx分别是关于t和x的全微分。

考虑方程式(9)，关于方程组式(8)的伴随方程是：

(11)

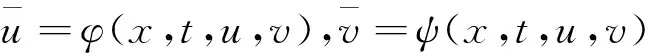
(12)

与λi1F1+λi2F2(i=1，2)相同，其中φ(x，t，u，v)≠0或ψ(x，t，u，v)≠0，则方程式(10)是非线性伴随的。换句话说，如果伴随方程组满足下列条件：

(13)

其中λij是未确定的系数，则方程组式(11)是非线性伴随的。

λ11=-φu，λ12=-φv，λ21=-ψu，λ22=-ψv，其中，φ和ψ满足下列方程组：

解上述方程组，有下列4种情形：

(1) 当p3≠0和α(t)≠β(t)时，

(14)

其中，ci(i=1，2，3)和k是任意的常数，方程组式(8)满足p1=-p3，p2=kp3。

(2) 当p3≠0和α(t)=β(t)时，

(15)

其中，ci(i=1，2，3)和k是任意的常数，方程组式(8)满足p1=2p3，p2=kp3。

(3) 当p3=0和p2≠0时，

(16)

其中，bi(i=1，2，3)和a是任意的常数。

(4) 当p3=0和p2=0时，

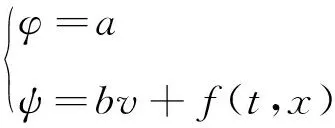
(17)

4 守恒定律

研究了广义变系Hirota-Satsuma方程组的守恒定律，用到以下定理。

定理1[6-7]有n个自变x=(x1，x2，…，xn)和m个因变量u=(u1，…，um)的s个方程方程组

Fα(x，u，u1，…，uN)=0，α=1，2，…，s

(18)

的任意无穷小对称(局部和非局部)有守恒定律Di(Ci)=0，这个守恒定律公式是：

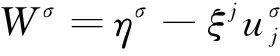
定理2 根据方程组式(8)的对称算子和它规范的拉格朗日形式，则方程组式(8)的一般的守恒定律DtCt+DxCx=0由下列公式给出：

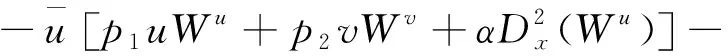
(19)

其中

Wu=ηu-ξtut-ξxux
Wv=ηv-ξtvt-ξxvx

通过对称分析的结果和定理2来计算方程组式(8)的守恒定律。

根据经典李群的理论[3]，方程组式(8)的对称可以写成下列形式：

根据定理2，有下列情形：

(1) 对于生成元

李的特征函数是：

可以从式(19)得到方程组式(8)的守恒向量：

α(2c1uxx+c1xuxxx)]+

β(2c1vxx+c1xvxxx)]+

(2) 对于生成元

李的特征函数是：

Wu=-c2ux
Wv=-c2vx

可以从式(19)得到方程组式(8)的守恒向量：

(3) 对于生成元

李的特征函数是：

可以从式(19)得到方程组式(8)的守恒向量：

(4) 对于生成元

李的特征函数是：

可以从式(19)得到方程组式(8)的守恒向量：

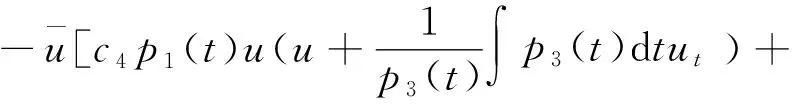
(5) 对于生成元

李的特征函数是：

Wu=0
Wv=c5v

可以从式(19)得到方程组式(8)的守恒向量：

6 结 论

基于广义变系数Hirota-Satsuma方程组的研究，对于理解非线性偏微分方程有了很大帮助。Hirota-Satsuma方程组的等价变换是增广空间上的一个非退化点变换，通过计算求解出方程组的等价代数。利用李经典对称分析法求出Hirota-Satsuma方程组的对称，并利用Ibragimov相关理论证明了这个方程组是非线性伴随的。最后利用方程组的伴随方程和Lie对称求出了方程组的无穷多个守恒定律，求出的守恒定律对于研究非线性偏微分方程的可积性具有重要意义。

参考文献(References)：

[1] DE L R，GANDARIAS M L. Equivalence Transformations and Conservation Laws for a Generalized Variable-coefficient Gardner Equation[J].Commun Nonlinear Sci Numer Simulat，2016，40：71-79

[2] SINGH K，GUPTA R.Lie Symmetries and Exact Solutions of A New Generalized Hirota-Satsuma Coupled KdV System with Variable Coefficients[J].International Journal of Engineering Science，2006， 44：241-255

[3] OLVER P J.Application of Lie Group to Differential Equation[M].New York：Sprin-ger，1986

[4] BLUMAN G W，ANCO S C.Symmetry and Integration Methods for Differential Equations[M]. New York：Springer，2002

[5] MALEK M，AMIN A M.Lie Group Method for Solving Generalized Hirota-Satsuma Coupled Korteweg-de Vries(KdV) Equations[J].Applied Mathematics and Computation，2013， 24：501-516

[6] IBRAGIMOV N H.A New Conservation Theorem[J].Journal of Mathematical Analysis and Applications，2006，33：311-328

[7] IBRAGIMOV N H.Nonlinear Self-adjointness and Conservation Laws[J].Journal of Physics A Mathematical & Theoretical，2011，44：4109-4112