随机丢失响应的半参数变系数部分非线性模型的估计*

张 文 佳

(南京理工大学 理学院，南京 210094)

0 引 言

作为非参数回归模型的演化版本，许多学者已经对其进行过研究。为了充分利用已知数据中的有效信息，考虑半参数变系数部分非线性模型， 它可以定义为

Y=XTα(U)+g(Z，β)+ε

(1)

其中α(·)=(α1(·)，α2(·)，…，αp(·))T是一个p维未知变系数函数，β=(β1，β2，…，βr)T是一个r维未知向量。Y是响应变量，(X，Z)∈Rp×Rq及U∈R是协变量。为了避免维数祸根，一般简单假设U是单变量。ε是模型的随机误差且与协变量(X，Z，U)独立，其期望和方差分别满足E(ε|X，Z，U)=0，E(ε2|X，Z，U)=σ2。g(Z，β)是已知的非线性函数，且Z和β不需要具有相同的维度。

变系数部分线性模型是最常见的半参数模型，被广泛研究。ZHOU X和YOU J H[1]，ZHAO P和XUE L G[2]及AHMAD I等[3]阐述了这种模型的许多经典方法、例子和应用。但在该模型中响应变量Y和协变量Z之间的关系是线性的，这可能会增加模型估计过程中的误差。因此，LI T Z和MEI C L[4]提出了变系数部分非线性模型。该模型包含许多其他重要的模型。例如，如果作为未知参数向量的α(·)≡α，或者p=1和X=1，则模型式(1)成为部分非线性模型。参见文献[5]，研究了带有变量误差的模型。若g(·；·)=0，则模型式(1)化为早期就开始研究的变系数模型，参见文献[6-7]，提出了一些基本的推断方法。此外，当模型式(1)中的g(Z，β)=ZTβ时，即为变系数部分线性模型。因此，模型式(1)既有变系数模型的灵活性又有非线性模型的便于理解的特性。

目前的研究旨在用完整的数据集来估计模型式(1)，然而在做观测研究时，研究中的一些变量值可能会丢失，因此完全数据集通常的推断过程不能直接被应用。许多作者在不同的回归函数中研究了缺失数据的回归分析。例如，ZHAO P X和XUE L G[8]研究了随机缺失响应变量的变系数部分线性模型的经验似然估计。WANG Q H等[9]探讨了缺失数据下的半参数回归模型的估计。XU W L和GUO X[10]对响应变量缺失下的变系数模型进行了非参数检验。牛翔宇和冯予[11]研究了数据缺失情况下广义非线性回归模型的统计诊断问题。

关于模型式(1)，LI T Z和MEI C L[4]通过结合局部线性估计及剖面最小二乘估计的方法来估计未知系数函数α(·)和未知参数β。QIAN Y Y和HUANG Z S[12]讨论了具有测量误差的模型，并建立了一个GLR统计量来判断α(·)是否是一个常数。本文提出了一种线性近似方法来估计随机丢失响应的模型式(1)的参数。通过样条法将可变系数部分转换为线性模型，并通过泰勒展开将非线性部分转换为线性模型。最后，基于插补的思想得到估计方程，然后用牛顿迭代法回归方程，得到α(·)和β的收敛估计。

1 估计过程

因此有：

(2)

1.1 线性近似

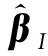
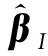
(3)

g(Z(i+1)，β)+g(Z(i)，β)}2

(4)

1.2 样条估计

经过第一步的转换，模型化为变系数部分线性模型。令M阶B样条的基函数为B(u)=(B1(u)，B2(u)，…，BL(u))T，其中L=K+M，K是节点的数量。取αk(u)≈B(u)Tγk，k=1，2，…，p。当Xi可以被完整观测到时，代入式(3)，可以得到：

(5)

(6)

其中：

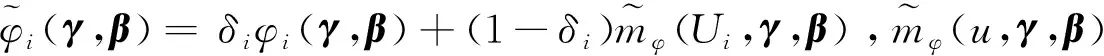
(7)

K(·)是一个核函数，h是带宽。

接下来研究得到估计量的渐近性质。令α0(·)和β0是α(·)和β的真实值。为了不失一般性，假设αk0(·)=0，k=d+1，d+2，…，p，且αk0(·)，k=1，2，…，d是α0(·)的所有非0部分。此外，假设βl0=0，l=s+1，s+2，…，q，且βl0，l=1，2，…，s是β0的所有非0部分。以下定理给出了估计量的一致性：

其中r在条件C1中定义。

从定理可以看出，通过选择适当的调整参数，估计过程是一致的，非参数分量的估计量就像真实零系数的子集一样已经达到最佳收敛速度，参见文献[14]。

(7)

2 定理证明

为方便起见，令C表示正数，每次出现可表示不同的值。下面首先给出下列正则条件。

C1：α(u)在(0，1)上r次连续微分，其中r>1/2。

C2：U的密度函数由f(u)表示，它在[0，1]上是0到无穷大，此外，假设f(u)在(0，1)上是连续可微的。

C3：记G1(u)=E(ZZT|U=u)，G2(u)=E(XXT|U=u)。因此对于u，G1(u)，G2(u)及，E(ε|U=u)是连续的。此外，对于给定的u，G1(u)和G2(u)是正定矩阵，且它们的和的特征值是有界的。

C4：定义τ1，τ2，…，τK为[0，1]的内部节点。取τ0=0，τK+1=1，hi=τi-τi-1，则存在一个常数C0满足：

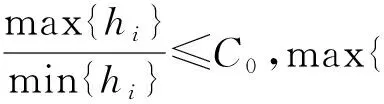
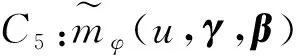
这些条件在非参数的文献中很常见。 条件C4意味着τ1，τ2，…，τK按顺序均匀分割[0，1]。 这些条件类似于文献[2]中使用的条件。

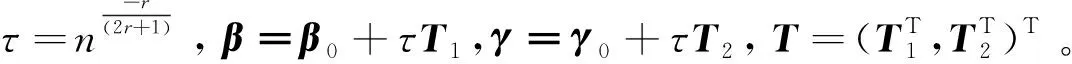
为了证明结论，首先需要证明给任意的ε>0，存在一个足够大的常数C使：

(8)

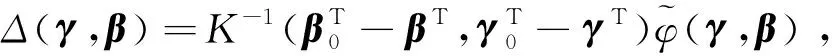
此外可以证明：

其中R(u)=(R1(u)，R2(u)，…，Rp(u))T，且Rk(u)=αk(u)-B(u)Tγk，k=1，2，…，p。由条件C1，C4及文献[15]的推论6.21，有‖Rk(u)‖=O(K-r)。因此由φi(γ，β)的定义式可得：

=I11+I12+I13+I14

由条件C3，并经过简单的化简可得：

=OP(τnK-1-r)‖T‖=OP(‖T‖)

因此得到：

I13=OP(τ2nK-1)‖T‖2=OP(‖T‖2)，

(2)由上一部分的证明可得：

综上所述，命题得证。

3 数值模拟

数据由半参数回归模型式(1)生成：Y=XTα(U)+g(Z，β)+ε，其中g(Z，β)=3(ZTβ)2，β=1.3及α(U)=(4U)3-eU+10.8，协变量X～N(1，1)，协变量Z和U分别服从平均值为-2，方差为2的正态分布，及均匀分布U(0，1)。ε是正态分布N(0，0.5)的模型误差。 样本大小n设置为100和300。本文对不同大小的样本分别运用了3组缺失概率，通过模拟的情况，来验证提出的估计方法。

首先对不同样本大小的数据进行模拟，然后在两种样本容量中对具有不同缺失率的数据进行模拟，为了更清楚地观察α(·)的模拟，将缺失数据下的3组拟合曲线、完整数据下获得的拟合曲线及其对应的实际曲线放在一张图中作对比(见图1)。

从图1可以看出，样本容量的大小对拟合精度有显著的影响。随着样本量的增加，拟合过程中数据缺失的偏差和影响减小。 此外，估计量的准确性随着缺失率的增加而降低。 模拟结果报告在表1中。

可以看出，随着U的变化，当α(U)的值在较小的范围内变化时，数据的浮动对估计结果有很大的影响； 相反，估计曲线将相对准确。且基于上述结果，可以知道数据缺失的概率越大，得到的数据分散度越大。此外，可以看到，β的估计比α(·)部分更准确。 随着样本量增加，缺失率的降低，准确率提高。

(a)a1缺失10%的数据及拟合曲线 (b)a2缺失20%的数据及拟合曲线 (c)a3缺失30%的数据及拟合曲线 (d)a4拟合曲线合并

(e)b1缺失10%的数据及拟合曲线 (f)b2缺失20%的数 (g)b3缺失10%的数据及据及拟合曲线 (h)b4拟合曲线合拟合曲线

图1样本量分别为100(ai)和300(bi)时不同缺失率下的拟合曲线

Fig.1Thefittingcurvesofthesampleswith100(ai)and300(bi)，respectively

注：a4、b4中实线代表真实曲线，虚线代表在完整数据下的拟合，点线、点划线和长虚线是对缺失率分别为10%、20%、30%的数据下进行拟合的曲线。

表1 在不同样本容量与不同缺失率下β与γ的估计值

4 结 论

基于变系数部分非线性回归模型，首先，结合了非线性最小二乘与插补的方法，给出了β的初始估计；其次，运用泰勒展开与样条估计，将函数g(·)与X的变系数分别化为β与x的线性模型；然后，用插补的思想，结合文献[8]，运用牛顿迭代的方法对感兴趣的参数进行估计。将线性近似方法与随机缺失响应变量的变系数部分非线性模型的样条估计方程相结合，可以解决更复杂的模型且便于理解并且操作简单，得到了估计量较好的渐进性质。模拟的两组结果显示了方法具有良好的回归结果，两个步骤在有限样本中表现良好，并随着样本数据量的增加及缺失率的降低，估计的精确性提高。

参考文献(References)：

[1] ZHOU X，YOU J H. Wavelet Estimation in Varying-coeffcient Partially Linear Regression Models[J].Statistics and Probability Letters，2004，68(1)：91-104

[2] ZHAO P，XUE L G. Variable Selection for Semiparametric Varying-coefficient Partially Linear Models with Missing Response at Random[J].Acta Mathematica Sinica (English Series)， 2011， 27(11)：2205-2216

[3] AHMAD I，LEELAHANON S，LI Q. Efficient Estimation of a Semiparametric Partially Linear Varying Coefficient Model[J].Institute of Mathematical Statistics in the Annals of Statistics， 2005， 33(1)：258-283

[4] LI T Z，MEI C L. Estimation and Inference for Varying-coefficient Partially Nonlinear Models[J]. Journal of Statistical Planning and Inference， 2013， 143 (11)：2023-2037

[5] FENG S Y，LI G R，ZHANG J H. Efficient Statistical Inference for Partially Nonlinear Errors-in-variables Models[J].Acta Mathematica Sinica(English Series)， 2014， 30(9)：1606-1620

[6] FAN J Q，ZHANG W Y. Statistical Estimation in Varying-coefficient Models[J].The Annals of Statistics， 1999， 27(5)：1491-1518

[7] CAI Z W，FAN J Q，LI R Z. Effcient Estimation and Inferences for Varying-coefficient Models[J].Journal of the American Statistical Association， 2000， 95(451)：888-902

[8] ZHAO P X， XUE L G. Empirical Likelihood Inferences for Semiparametric Varying -coefficient Partially Linear Models with Missing Responses at Random[J].Chinese Journal of Engineering Mathematics， 2010， 27(5)：771-780

[10] XU W L， GUO X. Nonparametric Checks for Varying Coefficient Models with Missing Response at Random[J].Metrika， 2016， 76(4)：459-482

[11] 牛翔宇，冯予.缺失数据下广义非线性回归的经验似然及诊断[J].重庆工商大学学报(自然科学版)，2016，33(6)：15-21

NIU X Y，FENG Y. Empirical Likelihood and Diagnosis of Generalized Nonlinear Regression under Data Missing[J]. Journal of Chongqing Technology and Business University(Naturnal Science Edition)， 2016，33(6)：15-21

[12] QIAN Y Y，HUANG Z S. Statistical Inference for a Varying-coefficient Partially Nonlinear Model with Measurement Errors[J].Statistical Methodology， 2016， 103(483)：1187-1199

[13] YATCHEW A. An Elementary Estimator of the Partial Linear Model[J].Econometric Letters， 1997， 57(2)： 135-143

[14] TANG Q G，CHENG L S. M-estimation and B-spline Approximation for Varying-coeffic-ient Models with Longitudinal Data[J].Journal of Nonparametric Statistics， 2008， 20(7)： 611-625

[15] SCHUMAKER L L. Spline Functions[M].New York： Wiley， 1981

[16] LI R Z， NIE L. Efficient Statistical Inference Procedures for Partially Nonlinear Models and Their Applications[J].International Biometric Society， 2008， 64(3)： 904-911