无原子可测集的一个注记*
2018-07-10曾小林吴明智
曾小林, 吴明智
(1.重庆工商大学 数学与统计学院, 重庆 400067; 2.中国地质大学(武汉) 数学与物理学院,武汉 430074)
0 引 言
测度论中,原子是一个很基础的概念。给定一个测度空间(Ω,F,P),设A∈F,A⊂Ω,如果P(A)>0且对A的任意可测子集B,要么P(B)=0, 要么P(B)=P(A),则称A为一个P-原子,简称为原子[1];如果A的任意可测子集B都不是原子,就称A是一个无原子可测集。原子的数学定义与经典物理学中的原子概念是一致的:原子里面除了它自己以外,不含比它还小的原子。
如果测度P对应的σ-代数F中没有任何原子,就称P为非原子测度。当提到无原子可测集时,不言自明地有一个测度,将它限制在无原子可测集上就可形成一个非原子测度。所以为了简洁起见,专注于讨论无原子可测集。
1922年,SIERPINSKI W建立了如下定理。
定理1 设(Ω,F,P)是一个测度空间,A∈F是一个无原子可测集,使得P(A)=a>0,那么对任意实数b∈[0,a],存在B∈F,B⊂A使P(B)=b。尽管这个定理看起来很简单,但是它的证明相当复杂,即使经过后人大量简化,依然需要使用很专门的知识和高超的技巧[2]。
原子的概念在随机赋范模理论的研究中常被用到。比如:随机赋范模中的Banach-Alaoglu定理与BBKS定理[3]的研究、从闭区间到完备随机赋范模的抽象值函数Riemann可积性的进一步研究[4]、各种随机共轭空间关系的深入讨论[5]、随机赋范模上非零连续线性泛函的存在性[6]等。在研究可测函数的分布函数与非增函数的重排函数时,程民德等[7]学者在其专著中也使用了定理1。
鉴于原子这一基础概念在随机泛函分析和实分析中的重要性,它的基本性质引起格外关注。针对测度在无原子可测集上的取值问题,提出两个新的命题,即第2节的命题2,3进行详细讨论,从而对定理1给出一种新的证明,同时也完善了人们对文献[7]中相应问题的认识。
1 预备知识
随机变量集合的性质,如同数学分析中实数集的性质一样,在相关研究领域中扮演重要的角色。考虑(Ω,F,P)上的实值随机变量全体形成的集合L0(F,R),下述重要命题是众所周知的:
命题1[8]设D是L0(F,R)中的某个非空集合,则必有D的可数子集{an,n≥1},{bn,n≥1},使得∨D=∨n≥1an,∧D=∧n≥1bn。
进一步,如果D关于L0(F,R)中的序≤是上(下)定向的,那么上述序列{an,n≥1}({bn,n≥1})可以选为关于序≤是非降的(非增的),相应结论简记为an↑∨D(bn↓∧D)。
所谓的上定向是指:如果a,b∈D,则存在c∈D使得a≤c,b≤c。下定向是指:如果a,b∈D,则存在d∈D使得d≤a,d≤b。
而L0(F,R)中的序≤是几乎处处意义下的不等式关系。涉及随机变量的运算都是几乎处处意义下的,不再一一指明。
2 主要结果及其证明
引理1 设(Ω,F,P)是一个测度空间,A∈F 是一个无原子可测集,使得P(A)=a>0,则存在A1∈F,使得A1⊂A且P(A1)∈[a/3,2a/3]。
证明(反证法)假设对任意C∈F,C⊂A有P(C)2a/3。
因A中无原子,必存在B∈F,B⊂A使得0 0 当0 注意集族C(C0) = {D∈F|D⊂C0,2a/3 令ξ= ∧{ID:D∈C(C0)} 先证{ID:D∈C(C0)}是下定向的。事实上,任取D1,D2∈C(C0),则Di⊂C0,2a/3 P(D1)-P(C0D2)>2a3-a/3=a/3。 仍然由反证假设知P(D1∩D2)>2a/3,所以D1∩D2∈C(C0),显然IDi≥ID1∩D2,i=1,2,因此{ID:D∈C(C0)}是下定向的。 命题2 设(Ω,F,P)是一个测度空间,A∈F 是一个无原子可测集,使得P(A)=a>0,则A中存在单调不增的子集列{An,n≥1}⊂F满足P(An)∈[a/3n,2na/3n]。 证明(数学归纳法)对集A运用引理1得:存在A1∈F,使得A1⊂A且P(A1)∈[a/3,2a/3]。记P(A1)=a1。 假设对n=k,存在A1,A2,…,Ak∈F使得Ak⊂Ak-1⊂…⊂A1⊂A且P(Ak)∈[a/3k,2ka/3k],记P(Ak)=ak,对集Ak运用引理1得:存在Ak+1∈F,使得Ak+1⊂Ak且P(Ak+1)∈[ak/3,2ak/3],由于ak∈[a/3k,2ka/3k],故得P(Ak+1)∈[a/3k+1,2k+1a/3k+1]。证毕。 命题3 设(Ω,F,P)是一个测度空间,A∈F 是一个无原子可测集,使得P(A)≥λ>0,则存在C∈F,使得C⊂A且λ/3≤P(C)≤2λ/3。 证明(反证法)假设对任意C∈F,C⊂A有P(C)<λ/3或P(C)>2λ/3。 观察集族G = {C∈F|C⊂A,0 令η= ∨{IC∶C∈C},类似引理1中的证明,易得对任意的C1,C2∈C,有C1∪C2∈C,从而易知集合{IC∶C∈G}是上定向的。 当P(F)=λ/3时,结论成立。 当P(F)<λ/3时,注意P(AF)=P(A)-P(F)>λ-λ/3=2λ/3,记P(AF)=b>0, 对集AF运用命题2得:AF中存在单调不增的子集列{Bn,n≥1}⊂F 满足P(Bn)∈[b/3n,2nb/3n]。故当n充分大时,0 下面给出定理1的一种新证明。 定理1之证先用数学归纳法证明事实(1): (1) 归纳基础:不失一般性设0 (n=2,…k)。只需证存在满足条件的Ck+1。 事实(1)得证。 注记1 文献[7]第163页给出了定理1的另一个巧妙证明,依赖于可测集剖分和实数集上确界技巧。但需要指出的是,那个证明过程中F1,F2,…,Fn如果只含空集∅,方法将会失效。人们自然会问这种情况可能出现吗?利用命题2立即可以看出这是不可能的。主要结果的证明中所采用的反证法和分情形讨论法在实变函数、高等概率论的研究中也是很普遍的。 利用下定向的随机变量集合的下确界性质,通过对可测集细致的剖分,结合可测集的性质、测度的有限可加性与从上连续性,凭借反证法证明了测度为正数a的无原子可测集中必存在某个可测子集,使得其测度落在区间[a/3,2a/3]内。然后,用数学归纳法证明了无原子可测集中必有一个单调不增的子集列,使得对无论多小的正实数区间,子集列中总存在某个集,其测度落在区间内。接着,以上述结论与类似方法为基础,证明了测度不小于某正实数λ的无原子可测集中必存在某可测子集,使得其测度落在区间[λ/3,2λ/3]内。进一步给出下述经典事实的一个新证明:如果0 参考文献(References): [1] 刘培德. 鞅与Banach空间几何学[M]. 北京:科学出版社,2007 LIU P D. Martingale and the Geometry of Banach Spaces[M]. Beijing: Science Press, 2007 [2] FRYSZKOWSKI A. Fixed Point Theory for Decomposable Sets[M]. New York: Springer, 2005 [3] GUO T X. The Relation of Banach-Alaoglu Theorem and Banach-Bourbaki-Kakutani-Smulian Theorem in Complete Random Normed Modules to Stratification Structure[J]. Science in China Series A: Mathematics, 2008, 51(9): 1651-1663 [4] 吴明智. 关于从闭区间到完备随机赋范模的抽象值函数的Riemann 可积性的进一步研究[J]. 中国科学:数学,2012, 42(9):897-903 WU M Z. A Further Study on the Riemann-integrability for Abstract-valued Functions from A Closed Real Interval to A Complete Random Normed Module[J]. Scientia Sinica Mathematica, 2012, 42(9):897-903 [5] GUO T X,ZHAO S E. On the Random Conjugate Spaces of A Random Locally Convex Module[J].Acta Mathematica Sinica,English Series, 2012,28(4): 687-696 [6] 郭铁信,曾小林. 随机赋范模上非零连续线性泛函的存在性[J]. 工程数学学报,2008, 25(1):117-123 GUO T X, ZENG X L. Existence of Nonzero Continuous Linear Functionals on Complete Random Normed Modules[J]. Chinese Journal of Engineering Mathematics, 2008, 25(1):117-123 [7] 程民德,邓东皋,龙瑞麟. 实分析(第2版) [M]. 北京:高等教育出版社,2008 CHENG M D, DENG D G, LONG R L. Real Analysis (2ndEdition) [M].Beijing:Higher Education Press, 2008 [8] DUNFORD N, SCHWARTZ J T. Linear Operators I[M]. New York: Interscience, 1957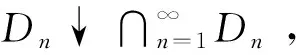
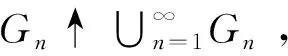
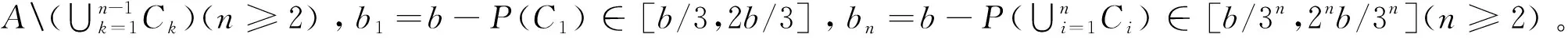
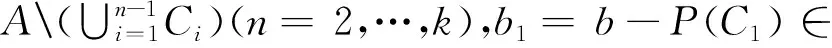
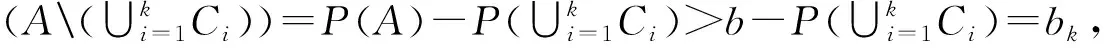
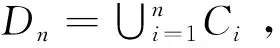
3 结束语
