例析求线段长度的几种方法

福建省泰宁县第四中学 温清梅

几何图形中的计算题是初中数学中常见题型，一直是数学中考的必考题型，求线段的长度正是这类计算题中的典型代表。纵观近年来的中考试题，求线段的长是中考中与图形有关的问题中经常会涉及的知识点，它在各市的中考压轴题中也常常涉及到。因此，能否掌握初中线段长的求解方法，将会影响到学生解决这些问题的能力。以下笔者将就一道题的多种解法谈谈求线段长度的方法。不难发现，解决途径都是运用转化的思想方法。要求学生自己探究、发现，寻求解决的途径。我在多年的初中教学中，特别是初三数学教学中，结合例题总结了几种常用的求线段的长度的方法。原题如下：

如图，在边长为1的正方形组成的6×6方格中，点A，B都在格点上。（1）在给定的方格中将线段AB平移到CD，使得四边形ABDC是矩形，且点C，D都落在格点上，画出四边形ABDC；（2）在方格中画出△ACD关于直线AD对称的△AED；（3）求出AB与DE的交点P到线段AD的距离。

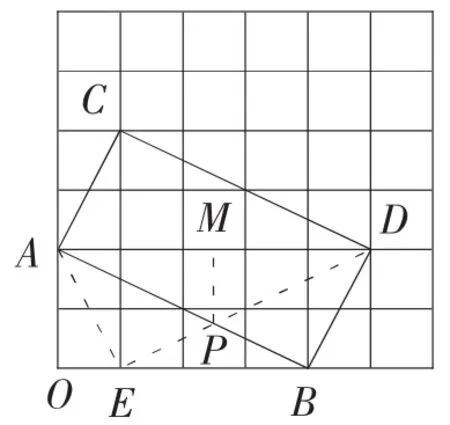
对线段长度的求解，则有多种方法，如解析法，相似三角形对应求线段比，等面积法，勾股定理以及相似三角形中的对应边的比等于相似比等方法。

一、解析法

在这里若以0为原点，0B所在直线为x轴，0A所在直线为y轴建立平面直角坐标系，此时A、B、D、E都在格点上，通过这几个点的坐标可以求出直线DE、AB的解析式，此时联合组成方程组就可以通过方程的解求出相应的P点的坐标，而坐标可以转化为长度，则可以求出P到AD的距离，这类解法得求出AB的解析式，ED的解析式，而后联立解析式，将它们看成方程（相应），求出方程的解，则是P点的坐标，再用A点的纵坐标减去P点纵坐标，得P点到AD的距离，方法较为繁琐，不得已才用这种方法。因为耗时耗力，一般不可取，但在抛物线与直线相交时，求线段的长段则基本要考虑这种方法，只要能求出直线与抛物线的交点坐标，便可以用纵坐标与纵坐标相减得到了，这是通法，当然，如果解析法熟练的同学这种方法可以节省许多思考的时间。

二、相似法

利用△APD∽△BPE，先由AD∥OB得到内错角相等，而后可由内错角相等和对顶角相等，得证△APD∽△BPE，对应高的比等于相似比，因此这里P至AD的距离比P到EB的距离即AD与EB的比，这里AO＝2，只设P到AD距离为x，而P到EB距离为（2-x），可列式求得x＝1.25，这种思路的理解，解法既简单又准确，是可以提倡的解法。利用相似三角形对应边成比例是求线段长度的常见方法，关键是找出所求线段和已知线段是哪两个三角形的边元素，再找寻出证明这两个三角形相似的方法，问题即可以解决。

三、勾股定理和相似结合的方法

首先，由各边的长度，如可知 AE2＝5，DE2＝20，AD2＝25，可知 AE2+DE2＝AD2，从而知道∠AED＝90°，过P作PM⊥AD，可知△PMD∽△AED，这里根据对称性可得AM＝DM，DM＝2.5，这里的PM就是我们所要求的，因此可列式即这里顺利的求出PM的值为1.25，这里的方法较第一种容易，但较第二种方法来说稍显繁琐。利用勾股定理求线段的长度关键是构建出直角三角形，再找出所求的线段是这个三角形的直角边还是斜边，或者它们的关系，就可以利用勾股定理求出所要求的线段长度。因此，相似和勾股结合的话会费时些，但是求线段常用的思路是相似和勾股，而许多同学也较常用，因此是较为提倡的好办法。

四、等面积法

运用面积关系解决平面几何体的方法，称为面积法。在此题中△APD的面积可以由AD乘以PM除以2得到，也可以由以PD为底，AE为高得到，AE为AD为5易求，而PD的求法叫可以由△ADP∽△BPE，得到这里求出PD，则再利用等面积式子，PD·AE＝AD·PM求得，这里PD的求法也可在△BPD中，利用勾股定理得到，但是方法较为麻烦。等面积方法不是最可取，但是它的这种思想方法将来会常用而且便捷，因此不失为一种好办法。等面积法常常会使题目简化，常见的有求直角三角形斜边上的高，常给出两直角边，可以利用勾股定理求出斜边，再求斜边上的高（用等面积法）。又常见与两条线段或三角线段相加之和，当没有办法将两条或三条线段转移到同一直线或边上时，常常会分解到两个三角形或三个三角形中，线段此时充当的角色是三角形的高，两个或三个三角形的面积等于一个三角形的面积，这时两线段或三角条段之和便转移到了总长上，它是几何中常用的一种方法。特点是把已知和未知各量用面积公式联系起来，通过运算达到求证的结果。所以用面积法来解几何题，几何元素之间关系会变成数量之间的关系。这个时候，问题就化繁为简了，只需要计算，有时甚至可以不添置辅助线就迎刃而解了。

此外，用面积法还可以用来证明线段相等（不等），角相等，比例式或等积式，求线段比等。虽然这些几乎都可以用其他方法来解决，但是面积法无疑是一种更直接、简易、有效的方法。

五、锐角三角函数法

在此题中，由于A、E、B、D在网格上，而且四边形A EBD是轴对称图形，因而可以求出AE、AD、DE的长度，从而可求∠AED＝90°，这样便得知∠ADE的正切值，过P作PM⊥AD，MD为AD一半，此时利用∠ADE的正切值，PM的长度则可解，在求线段长度的过程中，有时利用锐角函数值比用勾股定理和解析法在解题步骤上来得更为简便是值得推荐的方法。我们要理解在直角三角形中，当锐角一定时，它的对边与斜边、邻边与斜边、对边与邻边、邻边与对边的比值是固定的，这几个比值称为锐角三角函数，它反映的是两条线段的比值；它提示了三角形中的边角关系，这可以让我们找到相等角，在其他三角形中较快速地求出线段。

求线段的长度还有其他的一些方法，这几种方法只不过是平常较为常用的方法，在遇到类似问题时，教师可以多引导学生总结，归纳，具体情况具体分析，灵活运用数学思想方法来解决问题。