都是“直觉解题”惹的祸

浙江省绍兴市上虞区沥海镇中 张 薇

初中生初学平面几何，由于研究对象从数转到形，研究方法也从以运算为主转到以合情推理为主，又由于平面几何中新概念的大量集中出现，学生无论在知识的学习、技能和能力的形成，还是在学习方法和学习习惯培养等方面，都存在着相对不适应的状况。这无形中提高了几何入门的门槛。而《数学课程标准》在教学内容的安排上，变化最大的是几何教学提前，这更为几何入门教学增添了难度。因此，初学几何，尽管推理的能力已开始萌芽，但直觉、直观性操作、试验仍占主要地位，由于直觉思维具有自由性、灵活性、偶然性、不可靠性等特点，因而在我们的日常教学过程中，学生凭“直觉”“直观判断”等常规思维、经验解题，这里“直觉”起了举足轻重的作用，“直觉”是一把双刃剑，在解题中有时惹祸也确实不少。本文将通过一则案例，剖析“直觉解题”惹祸的内在原因，并提出一些化解对策。

案例：“平行四边形的判定”教学

赵老师施教的内容是浙教版八年级下册第五章第二节“平行四边形的判定”。教学中赵教师补充的一个推论是“如果一个四边形两组对角相等，则这个四边形是平行四边形”。即：已知在平行四边形ABCD中，∠A=∠C,∠B=∠D。求证四边形ABCD是平行四边形。（题目出示后，学生思考几分钟）

师：哪位同学能够说一下证明思路？

生1：连结 BD，我想证明∠1=∠2，因此来证明△ABD≌△BCD（如图1）。

师：请接着讲。

生 1：因为 BD=BD，AD=BC,AB=CD,

所以△ABD≌△BCD(SSS)，

所以∠1=∠2，于是AD∥BC。

同理，AB∥CD，

所以四边形ABCD是平行四边形。

师：为什么 AD=BC，AB=CD？

生1：四边形ABCD是平行四边形啊！所以对边相等。（还挺自信的）

师：同学们，我们的题目是要求证明四边形ABCD是平行四边形，你怎么说它已经是平行四边形了呢？那不是不用证了吗？请你坐下，再仔细想想。

（生1无言以对，一脸茫然地坐下。）

教师又叫了一位学生，问：你是怎么想的？

生2：过D、C两点分别向AB边作垂线段，我想证明高DH、CG相等，为此想证明△ADH≌△BGC。

在生2的证明中还是不知不觉地利用了“四边形ABCD是平行四边形”，证明失败之后，又企图证明DH=KB，还是没有成功（如图2）。

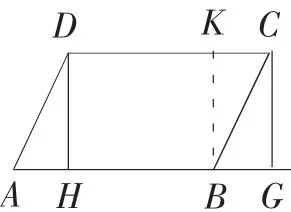
图2

接着，学生3作了两条高，企图证明DN=MB，为此想证明四边形MBND是矩形，也都失败了（如图3）。

图3

学生的这些“证明思路”都是无意之中默认了“四边形ABCD是平行四边形”的缘故。这显然都是直觉图形惹的祸！

剖析：

数学直觉作为数学学科的发端、数学学习的奠基石，它是数学学习有所发现、有所创造、有所发展的基础和前提，在数学学习中起着重要的作用。但是在初学几何的时候，由于学生对直观图形的认知相当直接、相当明白，因此它常常在学生的解题中惹起事端。因为几何的体系是从给出的已知条件出发，根据某些定理推到结论。解题中，学生所运用的依据只有两个：一是已知条件，二是已经学过的定理或定义等。图形里面看来正确的东西（我们姑且把它称为“图形信息”）是不能作为推理的依据的。但是由于学生尚处于借助直观进行初步的形象思维阶段，对这样的逻辑系统一时难以适应，于是就带来了有意无意地使用“图形信息”的错误，不经意间有时也常给我们教学惹祸。

化解对策：

在解题教学中，如何帮助学生克服这类低级错误？除了在遇到这种情况时能着力指出错误根源，帮助学生纠正之外，我们还可以采取如下的一些方法。

1.画“残缺图形”和“不正确图形”法。为了让学生不受或少受直觉的干扰，例如前面赵老师的课，如果教师把图形故意画成不正确的图（如图4），直觉的干扰可能会少些，当然也可以画成残缺图形。

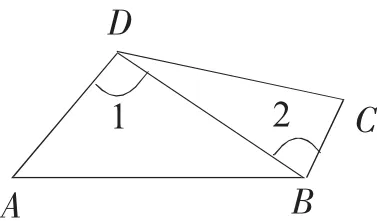
图4

2.通过不同途径，让学生多体会“眼见不一定为实”。

初学几何，学生往往凭直觉想当然。不认真分析题目的已知条件就草率下结论，从而导致错误。例如，比较图5两幅图形中线段AB与线段CD的大小。不少学生不假思索地回答AB小于CD。这时，教师不要急于否认学生的答案，可以组织学生自己亲自动手量一量或者教师利用几何画板等现代化教学手段显示出他们的实际长度，学生内心一定有强烈的震动，从而深切地体会到“眼见不一定为实”，直觉虽好但有时也会“惹祸不少”。

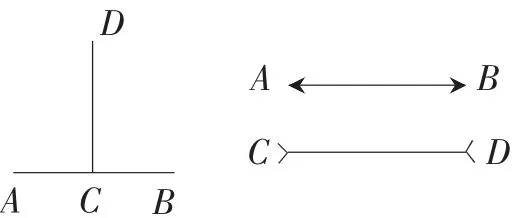
图5

通过观察、测量、计算、作图等实践活动，可以深化学生对数学的理解。所以在化解“直觉惹祸”的过程中一定要注意学生的主体参与，力争让学生多体验、多体会、多经历。只有经过参与其中的体验活动，学生才能真正做到将知识内化，转化为自己的知识。

3.举反例是化解“直觉解题惹祸”的重要途径。

反例在辨析错误中具有直观、说服力强等突出特点。在教学中，我们要注重反例的运用，这不但能使学生发现错误和漏洞，而且还可以修补相关知识，学会多角度考虑问题，从而提高思维的全面性。因此，在化解“直觉解题惹祸”的过程中，这是一种非常有效的“常规武器”。

例如，判断下列说法：“底面是正三角形，侧面均为等腰三角形的棱锥是正三棱锥。”是否正确？

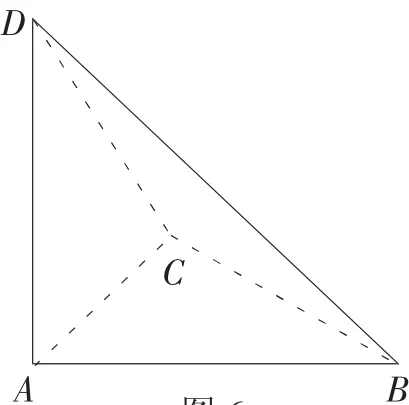
图6

这个命题绝大部分学生凭自己的直觉进行感知解题，觉得其正确性不容怀疑。但是条件“侧面是等腰三角形”并不等同于条件“侧面是全等的等腰三角形”。如图6，底面ABC是正三角形，DA垂直于平面 ABC，并且 DA=AB，这样侧面△ABD，△ACD均是等腰直角三角形，△DBC是等腰三角形，符合题设诸条件。但显然此棱锥不是正三棱锥。

数学家伊思·斯图尔特曾经说过：“数学的全部力量就在于直觉和严格性巧妙的结合在一起，受控制的精神和富有美感的逻辑。”受控制的精神和富有美感的逻辑正是数学的魅力所在，也是数学教育者努力的方向。在教学中，我们要充分发挥好直觉的威力，同时也游刃有余地化解“直觉解题所惹的祸”，充分发挥我们的聪明才智，为提高学生的数学思维和数学素养而不懈努力。

[1]郭允远.注意加强非逻辑思维训练[J].中学数学研究，2008.（2）.

[2]姚文孝.数学思想方法论选讲[M].长春：东北师范大学出版社，2001.