“一线三等角”问题学生解题调查
2018-07-10浙江省杭州市胜蓝中学吴莹莹
浙江省杭州市胜蓝中学 吴莹莹
一、原题呈现 题源分析
原题:如图 1,在 △ABC中,AB=AC=10,在BC边上取点D使BD=6,连结AD。以AD为一边作∠ADE=∠B交边AC于点E。若,求 cos∠AED的值。

图1

图2
题源分析:本题由两个简单图形组成,一个是腰长为10,底边长为16的等腰三角形,在浙教版九下课本P18例1能找到它的原型;另一个是书上常见的相似三角形。在浙教版九上数学书P135课内练习2能找到这组相似三角形。
1.如图2是某市“平改坡”工程中一种坡屋顶的设计图,已知原平屋顶的宽度l为10m,坡屋顶高度h为3.5m,求斜面钢条a的长度和坡角α(长度精确到0.1m,角度精确到1°)(浙教版教科书九下数学书P18例1)
2.如图,D为△ABC的边上一点,若要使△ABD与△ACB相似,可添加什么条件?你有几种不同方法?(浙教版教科书九上数学书P135课内练习2)
二、学生解法汇集
解法一:解:作AF⊥BC于点F,

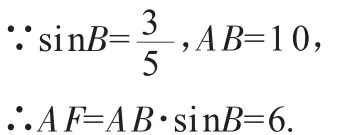
由勾股定理得:

由勾股定理得:

解法二:解:作AF⊥BC于点F,AG⊥DE于点G,
同解法一:BF=CF=8,

由勾股定理得
解法三:作AF⊥BC于点F,作DH⊥AC于点H,
同 解 法 二 得 :BF=8

解法四:作AF⊥BC于点F,作MA⊥AC交ED的延长线于点M.
同 解 法 三 得 :BF=8,△ABD≌△DCE,CE=BD=6,

三、数据分析
观成,朝晖,胜蓝,启航,江南实验共700名初三学生参加测试。笔者对各种数据作了汇总分析。

杭城5所初中本题解法及得分统计表
四、解法调查
1.课堂中要重视培养学生思维的灵活性。在调查中发现,观成跟江南实验两所学校得分率相对较高。这与学生本身的素质息息相关,也和教师的教法有关。教师在教学过程中只是一名学习的组织者,引导者与合作者。这样的教学方式改变了传统的教学模式——老师讲,学生听。马成瑞在《中学数学两种思维结合学习论》中阐述:数学中经常用到正向思维、逆向思维以及多向思维,体现了数学思维的灵活性。所以在课堂中培养学生思维的灵活性是非常重要的。
2.课堂中要重视培养学生思维的主动性。
每到初三,在传统教学模式中,往往逃不掉题海战术,试图通过学生不停地做题,以求学生对所学知识的灵活运用,从本次的调查中可看出这种做法收效甚微,在新课标下的教学模式,要求教师在教学过程中由主导为引导,如本题,如果直接求∠AED的余弦值是非常困难的,此时要求学生利用所学知识,在图中找到与∠AED相等的角,算出与之相等的角的余弦值,从而求得∠AED的余弦值。因此我们在教学过程中应该重视培养学生思维的主动性。
3.课堂中要重视培养学生思维的创造性。
本题中343位学生都想到了去构造以∠AED为内角的直角三角形。这样的定式思维把解题过程复杂化,从数据上也可以发现解法二、三的得分率较低。解法一更具创造性,得分率明显提高。新课标下,在教学过程中教师应该把数学思想方法慢慢渗透到每道题中,让学生自然而然找到最优解题方法。让我们更新教学观念,让学生创造性思维的火花在课堂上熠熠生辉。
解题时,既要注意一题多解,也要注意一题多变,更要重视多题一解,力求做一题通一类,做一类归一题,切实提高学习能力。通过本次对这“一线三等角”问题的调查,教师在日常教学中要重视培养学生思维的灵活性、主动性、创造性。充分发挥引导作用,让学生在自主学习的过程中快速有效地解答问题。
[1]教育部审定.义务教育教科书数学九年级上册[M].杭州:浙江教育出版社,2013.7.
[2]马成瑞.中学数学两种思维结合学习论[M].北京:教育科学出版社,2016.11.
