基于磨削力的磨削区表面温度场理论模型*

何玉辉， 冯 珂， 唐 楚， 唐进元

(1. 中南大学 机电工程学院， 长沙 410083)(2. 高性能复杂制造国家重点实验室， 长沙 410083)

磨削加工过程中，磨削温度超过临界值时会引起工件表面热损伤，如表面烧伤、材料氧化、残余应力和裂纹等，进而影响零件的使用寿命和工作性能，以及砂轮的使用寿命。因此，研究磨削温度，对改善表面质量、提高加工效率具有重要的理论意义和实际价值。

TOENSHOFF等[1]运用数学建模法研究磨削表面温度，以数学公式描述工件表层被磨去的物理过程，计算磨削热引起的表面温度升高及温度分布；该方法逻辑清晰、适用性广，但计算思路复杂，尚未被应用到实际加工中。ROWE[2]实验研究了低进给速度下的蠕动进给磨以及高进给速度下的高效大切深磨，提出一种估计温度量级的方法，但没建立磨削参数与磨削表面温度间的联系。MALKIN等[3]讨论了能量分配、热损伤的临界温度和热损伤建模，提出了关于磨削表面最高温度(MGT)的经验模型。席辉[4]用杯形砂轮平面磨削石英陶瓷，提出磨削表面温度与工艺参数的单因素经验公式，对温度分布建模做了初步探索。周德旺[5]以45号钢及灰铸铁为磨削加材料进行实验，研究其温度分布情况，将数据回归拟合，推导出了表面最高温度和加工参数相关的数学模型。李伟[6]等对碳纤维材料进行磨削加工时，考虑材料弹塑性变形，推算了该材料磨削温度的计算式；并用三元线性回归方法，推导了表面温度与3加工参数的回归模型，从而进一步分析各参数与磨削温度的相关性。

在磨削加工表面温度的理论建模研究中，多采用实验回归分析的方法，而从磨削力分析出发对磨削工件表面温度进行纯理论建模鲜见报道。因此，我们将磨削力分为切削变形力和摩擦力2部分，分别推导其同加工参数的关系，再计算这2个磨削力的切向分力，并结合切向磨削力与热源强度的关系，建立起磨削表面最高温度与加工参数的理论模型。运用热电偶完成磨削45号钢的测温实验，确定模型的常数。揭示磨削工艺参数对温度的影响趋势，为研究磨削力与磨削热耦合作用的残余应力场打下基础，也为合理选用磨削加工工艺参数提供理论依据。

1 理论建模

1.1 磨粒的磨削力分析

在磨削计算过程中，一般将磨削力分为切削变形力和摩擦力2部分，即：

Ft=Ftc+Fts

(1)

式中：Ft为切向磨削力，Ftc为由切削变形产生的切向力，Fts为由摩擦作用产生的切向力。

1.1.1 切削变形力

单颗磨粒切削模型如图1所示。图1a所示为单颗磨粒在切深为ap时的受力分析图。在忽略摩擦的情况下，单颗磨粒的切削力dFx垂直于磨粒锥面上，它可以划分为垂直方向上的法向力dFnx和水平方向上的切向力dFtx，其作用的范围如图1b中的虚线圈所示[7]。

依据图1可知，在X-X截面上单颗磨粒受到的切削力dFx可表示为：

dFx=Fp×dAcosθcosψ

(2)

式中：Fp为单位面积上的磨削力；θ为磨粒的半锥角；ψ为切削力方向与切削方向之间的夹角。

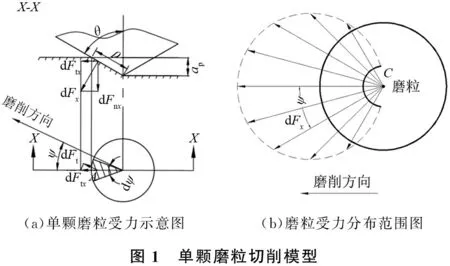
(a)单颗磨粒受力示意图(b)磨粒受力分布范围图图1 单颗磨粒切削模型

假设磨粒中心线沿砂轮直径方向指向砂轮中心，且其母线长度为ρ，则单颗磨粒与工件的切削面积

(3)

综合式(2)和式(3)得：

(4)

根据图1a可得：

(5)

将式(4)代入式(5)得：

(6)

依据图1b知：单颗磨粒受到的切削合力

(7)

其中：ψ1、ψ2分别为磨粒和工件接触的初始角与结束角。在一般磨削中，ψ1=-π/2，ψ2=π/2，由式(7)可以获得单颗磨粒由切削变形力产生的法向力和切削方向力：

(8)

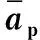
根据文献[8]，假定未变形磨屑厚度服从瑞利分布，在推算平均磨屑厚度的过程中假设：(1)砂轮磨粒可看作圆锥体，其顶锥角确定为2θ；(2)突出砂轮表面的磨粒都进行加工，且去除工件表面材料；(3)磨粒加工时产生完全切削，不考虑工件与砂轮的变形。求得：

(9)

将式(9)代入式(8)并乘以砂轮与工件接触区内的总磨粒数Nd，便可获得由切削变形力产生的切向力和法向力分别为：

(10)

1.1.2摩擦力

由磨削原理可知[9]，

(11)

(12)

式中：p0为常数，可通过实验确定。在平面磨削中，Δ=4vw/(dsvs)，表示磨粒实际参与磨削的轨迹的曲率半径与砂轮半径之差。

依据摩擦的二项式定理，摩擦因数μ可以表示为：

(13)

式中：α、β均为系数，由接触面的物理性能确定。

将式(13)代入(11)中，并乘以砂轮与工件接触区内的总体磨粒数Nd，得摩擦力的切向磨削力Fts

(14)

1.2 切向磨削力模型

综上分析，可得磨削由切削变形和摩擦共同作用引起的切向磨削力Ft

(15)

1.3 磨削区的最高温度模型

根据磨削原理，反映磨削温度场大小的最主要因素是热流密度，基于移动热源理论，磨削区单位时间单位磨削宽度的热流密度qw

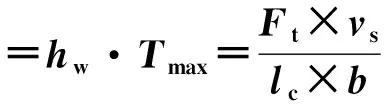
(16)

其中，对流因子可以表示为：

(17)

式中：λ为热导率，βw为热接触系数。

由此，ROWE[11]提出磨削区工件表面最高温度Tmax的公式如下：

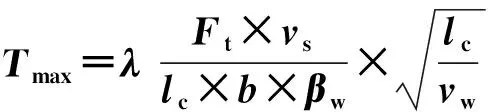
(18)

通过上述分析可知，表面最高温度可以和磨削工艺参数建立紧密的联系。将式(15)代入式(18)得：

2 实验验证

2.1 实验条件

磨削实验在超精密成型磨床MKL7132(如图2所示)上进行，主轴转速0～2500r/min，工件纵向最大行程650mm，横向最大行程230mm，连续进给速度0.1～1m/min。磨削实验条件如表1所示。砂轮参数如表2所示。由于此次磨削实验为小切深磨削，砂轮磨损不大，所以整个实验不用更换砂轮。

图2 成型磨床MKL7132

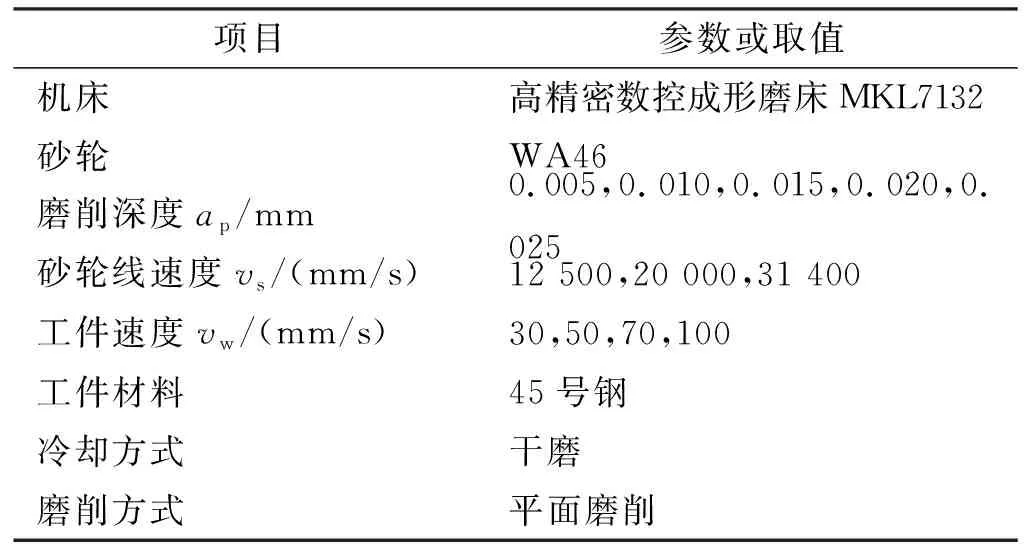
表1 磨削条件

表2 实验所用砂轮参数指标

2.2 实验装置

测温装备采用双极可磨热电偶。信号采集卡为OM-DAQ-USB-2401，一款全速USB 2.0热电偶/电压输入数据采集模块。热电偶传输的电动势信号传到信号采集卡，经信号放大和隔噪降噪处理，再传到电脑中，转换为可靠性高的温度信号。该温度信号直接在电脑中用Matlab进行绘图。磨削力和磨削温度测量系统示意图如图3所示。

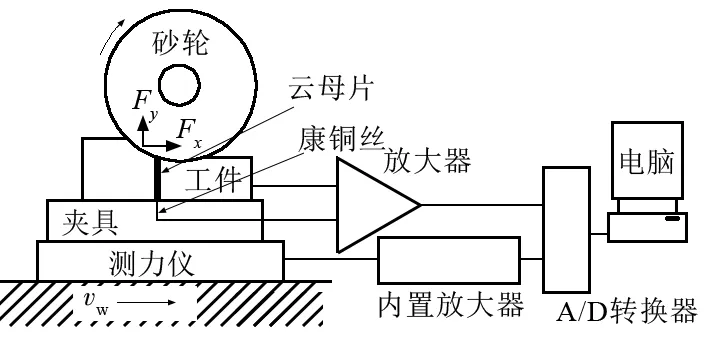
图3 磨削力和磨削温度测量系统示意图

磨削过程中，温度不断变化，而且这个变化时间很短。为准确测温，测温装置需要反应迅速。实验使用双极可磨热电偶装置，其在磨削过程中形成的热电偶结小，在传导温度的过程中迟滞效应小；且实验用的信号分析仪反应迅速，能满足测温要求。

使用双极可磨式热电偶，需要在工件上开单面槽，即先把待磨工件对等切开为A、B等2块，切后尺寸均为25 mm×20 mm×30 mm(长×宽×高)，再将结合面在抛光机上进行平磨和抛光，使再次配合时缝隙尽量小以减小测温误差；在一块磨块接合面上开安装槽，其大小和形状能够刚好嵌入热电偶即可。本次实验样件的尺寸如图4，内部开槽尺寸定为0.2 mm×0.1 mm。

图4 工件的几何尺寸

2.3 实验结果

模型磨削温度和实验温度数据如表3所示。

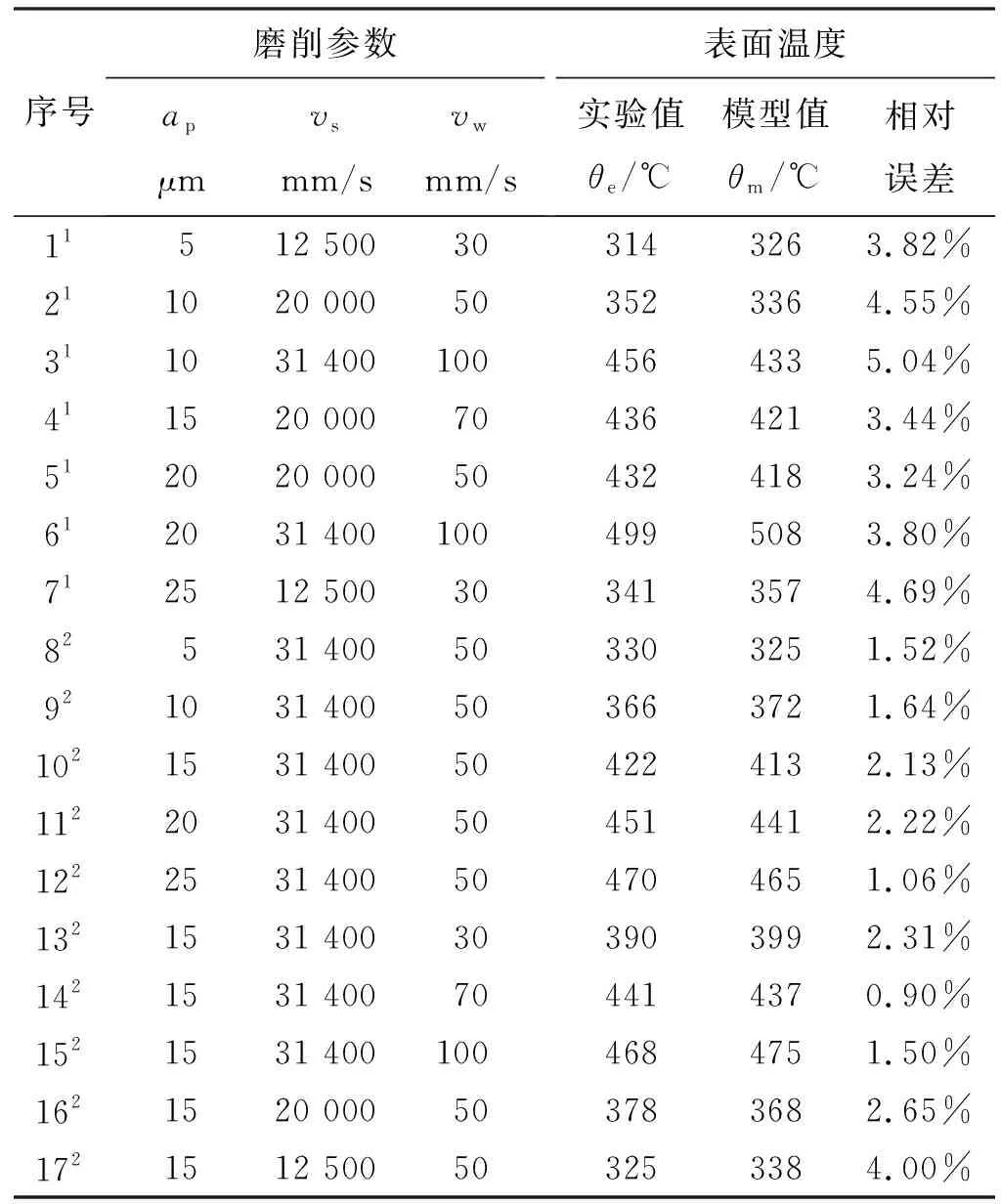
表3 不同磨削实验条件下的测试结果与预测结果

1：数据用于测定模型的常量；2：数据用于验证模型与实验吻合程度。

基于1stOpt计算软件，将表3中1～7组的测试结果代入式(20)，采用Levenberg-Marquart优化算法进行非线性拟合，得到磨削表面温度的拟合方程为：

另一方面，智能家居产品也提供了一种新型的早教形式。近两年，智能家居产品在科技的推动下逐渐渗透至年轻家庭生活的方方面面，其中母婴亲子类智能家居产品不仅能提供母婴知识，还能帮助宝宝学习知识，进行简单早教，因此广受欢迎。各类产品中最受追捧的智能家居产品是智能电视，家庭拥有比例为51%，远高于智能体重秤、智能可穿戴设备等其他智能产品。

2.4 结果与讨论

将表3中8～17组的数据代入式(21)可得：本次实验的表面温度模型值与实验结果之间的最大相对误差为5.04%，平均相对误差为2.47%。

其原因在于：(1)用管式电炉对热电偶进行测量标定，然后通过调节电炉的炉温大小来确定输出热电势，没有考虑实际加工时动态切削力的作用对热电势的影响；(2)热电偶测量磨削温度时有迟滞效应，且提取温度时经滤波处理，多次测量求平均值法只能减小误差而不能消除误差。

图5～图7为磨削表面温度预测值与实验值随加工参数变化的对比图。从图5～图7中可以看出：磨削表面温度的计算结果与实验结果随工件速度、磨削深度以及砂轮转速的变化趋势一致、数值接近，验证了模型的正确性。

(1)工件速度

磨削表面温度预测值与实验值随工件速度变化如图5所示。由图5可知：随vw增加，表面温度值相应升高。通过磨削温度模型得到的温度和实验得到的温度随工件速度的改变趋势是相同的，并且模型温度和实验温度相差不大。这是因为：当磨削深度ap和砂轮旋转线速度vs一定时，将砂轮与工件接触区看作移动热源，随着vw增大，磨粒与工件间的冲击力更大，挤压力增大，温度升高。

图5 磨削表面温度预测值与实验值随工件速度变化对比图

(2)磨削深度

由图6还可以得到：在磨削深度不断变大的过程中，温度的增幅在减小。因为随磨削深度变大，砂轮中参与磨削的磨粒变多，最后会达到饱和状态，所以温度的增幅降低。

图6 磨削表面温度预测值与实验值随磨削深度变化对比图

(3)砂轮速度

图7为模型磨削温度和实验温度随砂轮速度变化的对比图。由图7可知：随vs增大，表面温度线性升高。这是因为vs增加，单位时间内参与工件磨削的砂粒数量变多，总热流密度升高、磨削热变多，磨削温度也随之增大。

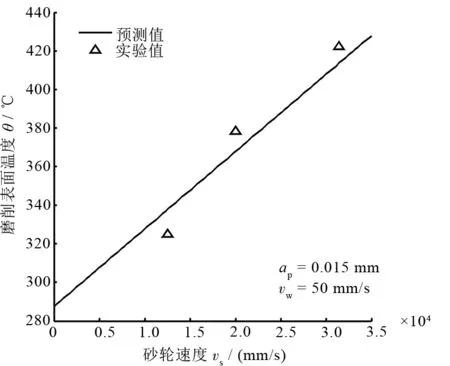
图7 磨削表面温度预测值与实验值随砂轮速度变化对比图

3 结论

假设未变形磨屑厚度服从瑞利分布，将磨削力分为切削变形力和摩擦力2部分，分别推导了摩擦力和切削变形力同加工参数的关系式，再计算这2个磨削力的切向分力，并结合切向磨削力与热源强度的关系，建立起磨削表面最高温度与加工参数的理论模型。然后在成型磨床MKL7132上进行加工45号钢的测温实验，研究表明：

(1)试件表面温度随着切深ap、进给速度vw和砂轮速度vs的增大而增大。

(2)在实验的工艺参数范围内，工件表面温度预测值与实验结果之间的最大相对误差为5.04%，平均相对误差为2.47%。

[1] TOENSHOFF H K, PETERS J, INASAKI I, et al. Modeling and simulation of grinding processes [J]. CIRP Annals-Manufacturing Technology, 1992, 41(2): 677-688.

[2] ROWE W B. Thermal analysis of high efficiency deep grinding [J]. Int. J. Mach. Tool. Manu., 2001, 41(1): 1-19.

[3] MALKIN S, GUO C. Thermal analysis of grinding [J]. CIRP Annals-Manufacturing Technology, 2007, 56(2): 760-782.

[4] 席辉. 杯形砂轮平面磨削温度场的实验研究及其仿真 [D]. 天津: 天津大学, 2007.

XI Hui. Experimental study of surface grinding temperature filed by cup wheel based on computer simulation [D]. Tianjin: Tianjin University, 2007.

[5] 周德旺. 平面磨削温度场的研究 [D]. 长沙: 湖南大学, 2008.

ZHOU Dewang. Study on the temperature field in surface grinding [D]. Changsha: Hunan University, 2008.

[6] 李伟. 碳纤维复合材料磨削温度理论分析与试验研究 [D]. 大连: 大连理工大学, 2008.

LI Wei. Theoretical analysis and experimental research on grinding temperature of carbon fiber reinforced composites [D]. Dalian: Dalian University of Technology, 2008.

[7] 李伯民, 赵波. 现代磨削技术 [M]. 北京: 机械工业出版社, 2003.

LI Bomin, ZHAO Bo. Modern grinding technology [M]. Beijing: Machinery Industry Press, 2003.

[8] 何玉辉, 唐楚, 唐进元, 等. 轴向超声振动辅助磨削的表面残余应力建模 [J]. 振动与冲击, 2017, 36(22): 185-191.

HE Yuhui, TANG Chu, TANG Jinyuan, et al. Modeling of grinding surface residual stress assisted with axial ultrasonic vibration [J]. J. Vibration and Shock, 2017, 36(22): 185-191.

[9] 任敬心, 华定安. 磨削原理 [M]. 北京: 电子工业出版社, 2011.

REN Jingxin, HUA Ding′an. Grinding principle [M]. Beijing: Publishing House of Electronics Industry, 2011.

[10] 傅杰才. 磨削原理与工艺 [M]. 长沙: 湖南大学出版社, 1986.

FU Jiecai. Grinding principle and technology [M]. Changsha: Hunan University Press, 1986.

[11] ROWE W B. Thermal analysis of high efficiency deep grinding [J]. Int. J. Mach. Tool. & Manu., 2001, 41(1): 1-19.