工件旋转磨削表面纹理数值预测模型分析*

曹治赫， 林 彬， 周 平， 康仁科

(大连理工大学， 精密与特种加工教育部重点实验室， 辽宁 大连 116024)

在电子工业中，工件旋转磨削被广泛应用于单晶硅等硬脆材料的加工上，是精密/超精密加工的核心技术之一；而芯片制造技术的飞速发展，对于硅片的表面及亚表面质量提出了越来越高的要求[1-2]。在硅片磨削过程中会不可避免地产生表面及亚表面损伤[3]，其表面纹理和损伤深度限制了后续加工流程的效率。因此，对磨削后工件的表面纹理特征、粗糙度和亚表面损伤进行准确预测，对磨削工艺的优化和磨削机理的研究都有着极为重要的意义。

磨削仿真模型主要包括砂轮模型与砂轮工件相互作用模型。随着测试技术的发展和计算机运算能力的提高，通过数值模拟方法已经可以模拟出被磨削工件表面磨痕的一些几何特征[4-7]。CHEN 等[8]在砂轮模型中假设球形磨粒在砂轮体内均匀分布，研究砂轮磨损特性对外圆磨削表面粗糙度的影响。ZHOU 等[9]同样使用球形磨粒均布的假设，根据外圆磨削中的运动学关系，研究磨削表面纹理及砂轮磨损对表面粗糙度的影响。AHEARNE 等[10]提出了工件旋转磨削条件下的二维工件形貌模型，仿真区为工件上的一段圆弧，研究了磨粒切深及表面粗糙度沿硅片径向位置变化的趋势，仿真结果与粗粒度砂轮磨削实验结果吻合较好。ZHOU 等[11-12]根据工件旋转磨削过程中的运动学关系，模拟工件表面磨痕密度分布，并研究了工件表面粗糙度沿径向变化的趋势及其与磨痕密度之间的关系。但是，目前尚未有能准确预测细粒度砂轮磨削工件的表面形貌及粗糙度的仿真模型。

我们基于现有的磨削纹理数值仿真模型[4, 10]，分析了工件旋转磨削表面的纹理特征，并与单晶硅片超精密旋转磨削的结果对比。鉴于超细粒度砂轮孔隙度高、磨粒易脱落，调整其实际有效磨粒数，并对数值仿真模型进行修正，将实验获得的表面纹理特征和文献报道的单磨粒纳米切深划擦实验研究成果结合，讨论了超细粒度砂轮磨削过程的数值仿真结果存在偏差的可能原因。

1 表面纹理的数值分析模型

1.1 仿真流程

工件旋转磨削是平面磨削的一种，其形式如图1所示：工件被吸附在带有真空吸盘的工作台上，砂轮轴与工件轴之间有一定的倾角来保证半弧磨削。这种磨削方式具有面形精度高、表面质量好、自动化程度高、成本低等优点，是目前集成电路领域广泛采用的超精密磨削方式。

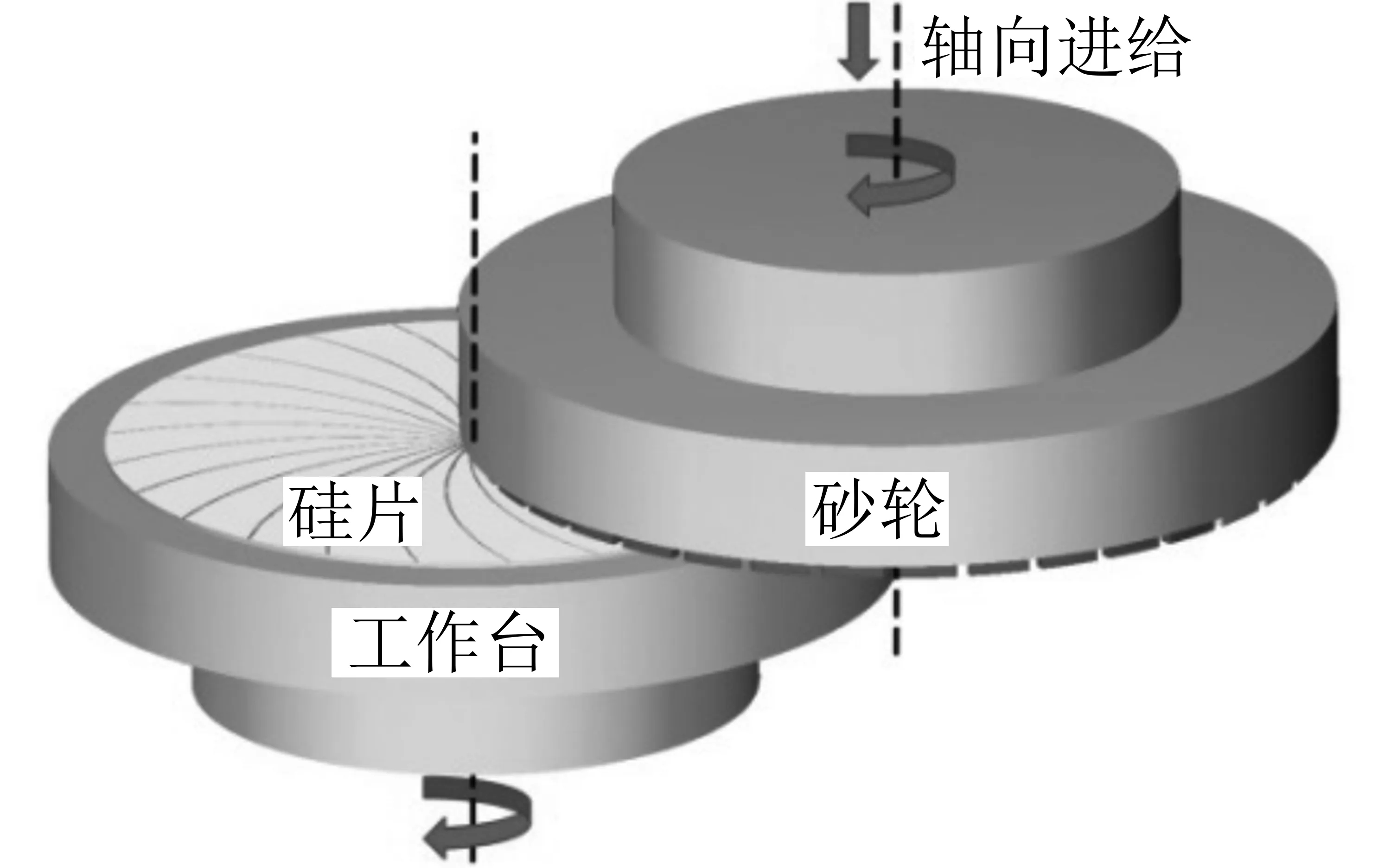
图1 工件旋转磨削

图2为仿真模型布置。为研究仿真结果随工件径向变化的趋势，沿工件直径方向共分布有5个仿真区。仿真模型运行流程如图3所示：输入砂轮参数与磨削参数后，首先计算对仿真区磨削一次过程中砂轮转过的角度，再设定砂轮上对应角度范围内磨粒的位置分布，随后计算这些磨粒对工件的切削作用。工件转过一周后判断磨粒切深是否稳定，如切深未稳定则按砂轮进给速度增加切深，对仿真区重新计算下一次磨削所需的砂轮磨粒分布，并重复此过程直至磨粒切深稳定。磨粒切深稳定时，说明磨削进入稳定磨削过程，这时可输出磨粒切深及仿真区工件形貌，完成磨削仿真过程。对每个仿真区重复此过程，直至整个磨削过程完成。

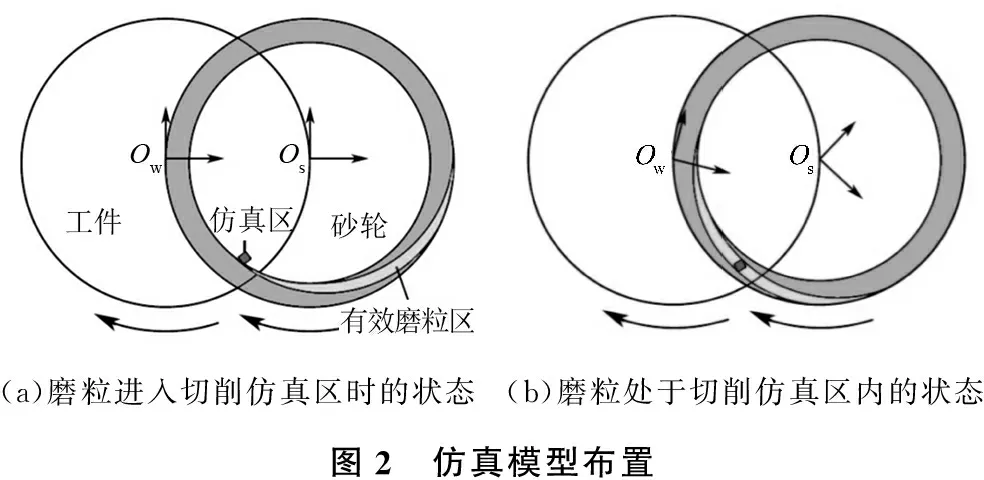
(a)磨粒进入切削仿真区时的状态(b)磨粒处于切削仿真区内的状态图2 仿真模型布置

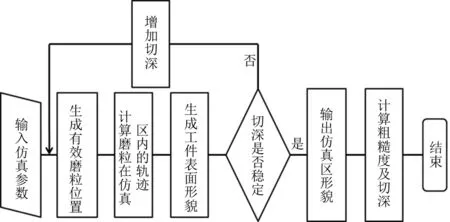
图3 模型运行流程

1.2 砂轮模型构建

球形磨粒假设在磨削仿真模型中广泛应用[4-7, 13]。我们假定有均一大小的等效球形磨粒随机均匀分布在砂轮基体内，且等效磨粒直径为dg。同时，假设磨粒中心点突出砂轮基体dg/4就会脱落，则磨粒中心点在Z方向的分布范围为0到3dg/4。

从图2中的仿真区位置可以看出：在工件旋转一周的过程中，只有一小段时间磨粒会对仿真区进行磨削。为了提高效率，只需计算出这段时间内砂轮转过的角度θ1就可以生成一个扇形的磨粒分布，而这些磨粒足够对仿真区进行磨削。在这个扇形磨粒分布区域内，总磨粒数目N可以由下式确定：

(1)

其中：vg是磨粒的体积浓度，Vs是砂轮上有磨粒分布区域的体积。在Vs内磨粒中心点的三维随机分布是均匀的，有效磨粒中心点突出砂轮基体的高度hcore应当满足：

dg/4≥hcore≥0

(2)

有效切削磨粒的位置记做集合O。为提高计算效率，在仿真磨粒对工件进行切削时再计算磨粒形貌。

超精密磨削砂轮内部存在较多的气孔，且表面的磨粒分布与仿真模型中假设的均匀分布并不一致[14]。此外，砂轮中磨粒粒度及形状的随机分布对砂轮有效磨粒数及磨粒凸出基体高度与数量等参数均有影响[15]。

1.3 构建砂轮工件相互作用模型

使用时序仿真模型，假设在工件旋转一周的时间内，仿真区开始接触磨粒区的时间为ts，仿真区离开磨粒区的时间为te，则需要对这个时间段内的每个时刻进行采样分析。要计算某时刻磨粒对仿真区的切削作用，首先要判断此时刻可能对仿真区进行磨削的磨粒在砂轮坐标系内的位置。假设工件仿真区中心点在工件坐标系内的坐标为(xw,yw)，将其转换到砂轮坐标系内，坐标转换式如下式：

(3)

式中：φs、φw分别为砂轮和工件从初始时刻到现在时刻转过的角度，lws为砂轮与工件的轴心距。

以点(xs,ys)为中心，在砂轮坐标系中取边长为2l的正方形，l为工件上仿真区边长；筛选之前生成的磨粒中心点坐标，选出位于正方形内的坐标点的集合P，保证集合P转换到工件坐标系中后能完全覆盖仿真区：

(4)

集合P内的点转换到工件坐标系后的坐标，就是实际磨削时在这一时刻磨粒在工件坐标系内的位置。由式(4)即可得到某采样时刻，集合P内所有磨粒中心点在工件坐标系上的分布情况。

磨粒对工件的弹塑性切削深度矩阵，可以用等效磨粒形貌矩阵数据与仿真区形貌矩阵数据，按下列公式进行计算：

hcut(m,n)=hmax-ap-h(i,j)

(5)

式中：hmax为集合O中磨粒最高点高度的最大值，ap为集合O中最高的磨粒对工件的未变形切深，h(i,j)为集合P内某个磨粒形貌矩阵的元素。若某点的切削深度计算值为负，则将其置为0。经过此时刻的切削后，仿真区形貌矩阵的变化由下式计算：

hw1(m,n)=hw(m,n)-hcut(m,n)

(6)

对工件旋转一周时间内每个切削时刻重复上述过程，就得到了工件旋转一周之后的仿真区形貌。为使仿真中磨粒分布更加合理，在工件旋转一周后、再旋转下一周之前，要重新生成磨粒中心点分布。

2 实验条件及方法

磨削验证实验在VG401 MKII型超精密磨床(Okamoto，日本)上进行，磨削工件为φ200 mm的(100)单晶抛光硅片(有研，中国)，使用的砂轮为不同粒度的陶瓷基金刚石杯型砂轮(Asahi，日本)，磨削过程冷却液为去离子水，磨削参数如表1所示。

表1 磨削及仿真参数

在硅片的实际生产过程中，硅片减薄到目标厚度后会进入光磨阶段后，砂轮停止轴向进给，仅依靠基体弹性变形产生的让刀量继续加工硅片，直至让刀量接近零。光磨过程会使硅片的表面形貌趋于一致，但是为了观察到不同磨削条件下硅片表面形貌的区别，在验证实验中，光磨时间被设置为零。

SD600砂轮磨削表面形貌使用美国ZYGO公司New View 5022型3D表面轮廓仪测量，SD1500和SD5000等2个砂轮的磨削表面粗糙度较小，其表面形貌使用韩国PARKER公司XE-200原子力显微镜测量。

3 仿真与实验结果分析与对比

3.1 磨粒平均切深分析

通过仿真研究磨粒平均切深随砂轮粒度的变化趋势。仿真参数如表1所示，仿真结果如图4所示。

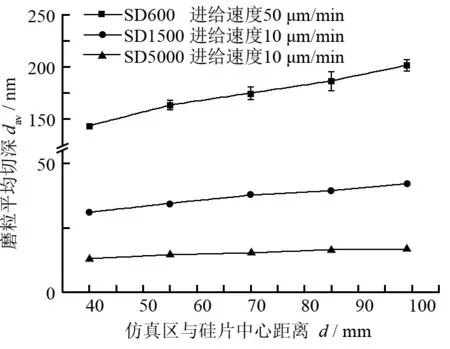
图4 磨粒平均切深沿硅片径向变化

如图4所示：磨粒平均切深均随着仿真区与硅片中心距离增大而增大，而且随着磨粒尺寸的增大，磨粒平均切深逐渐增大，粗糙度在径向变化的范围也随之增大。这一现象基本与现有文献中的变化趋势相吻合，但是磨粒切深却小于磨粒使工件产生塑性变形的切深。

WANG 等[16]对磨削过程中磨粒的状态进行了分析，根据Hertz接触公式提出了磨粒进入耕犁状态所需要的临界切深hplow，其表达式如下：

(7)

由式7计算可得SD5000、SD1500砂轮磨削时，磨粒进入耕犁状态的临界切深分别为18.1 nm、60.2 nm。从图4中可以发现：磨粒切深均小于对应的耕犁临界切深，即磨粒不能进入耕犁状态，更不可能对工件材料产生切削。因此，现有工件旋转磨削仿真模型应用于实际细粒度工件旋转磨削过程的预测尚有一定问题。

3.2 磨削表面纹理的验证

图5是10 μm/min进给速度下SD1500砂轮磨削硅片的测量纹理与仿真纹理。对比图5c、图5d可以发现：距离硅片中心较近的仿真区纹理比较散乱，而距离硅片中心较远的仿真区纹理相对有序，这与工件旋转磨削的原理相符合。但是对比仿真结果与测量结果的纹理特征可以发现：仿真结果与测量结果的纹理间距相差甚多。

3.3 磨削表面粗糙度的分析与验证

磨削验证实验的测量结果与基于现有模型假设的磨削仿真模型预测结果[4, 10]的对比如图6所示。

从图6中可以发现：基于现有工件旋转磨削仿真模型假设[4, 10]的磨削仿真结果与实验结果，不论在粗糙度数值还是沿硅片径向变化趋势上均有较大的差距。

(a) 距中心40 mm处的表面纹理(b) 距中心99 mm处的表面纹理(c) 距中心40 mm处的仿真结果(d) 距中心99 mm处的仿真结果图5 10 μm/min进给速度下SD1500砂轮与磨削仿真结果

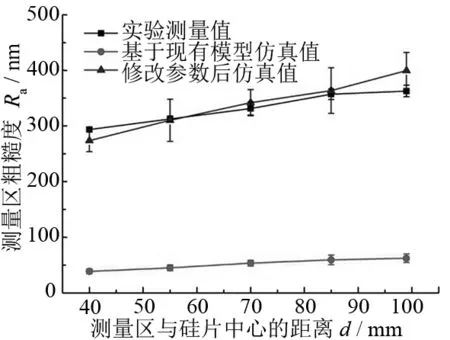
(a) SD600砂轮，进给速度50 μm/min

我们尝试对现有磨削仿真模型中的参数进行修正。通过仿真发现：当磨粒体积比变为原始值的1/40时，SD600砂轮仿真结果的粗糙度数值与沿硅片径向的变化都与实验结果吻合较好(图6a)。随磨粒直径变小，仿真结果与实验结果的差距逐渐变大。因此，现有磨削仿真模型不适于预测细粒度砂轮磨削过程。尽管修改磨粒体积比之后的仿真结果与实验结果较为接近，但是实际有效磨粒数只有计算有效磨粒数的1/40，这一论点仍然缺乏数据支撑：即使考虑到砂轮孔隙率以及磨粒半径变化对磨粒体积比的影响[15]，实际有效磨粒数也仅能变为计算有效磨粒数的1/5。因此，现有工件旋转磨削仿真模型应用于实际细粒度工件旋转磨削过程的预测尚有一定问题。

4 超精密磨削仿真模型存在的问题

在超精密磨削硅材料的过程中，为了控制脆性损伤，磨粒的切深一般都在几十纳米左右[17]，甚至控制在几纳米[18]。单颗粒划擦实验表明，当切深在这一范围时，单晶硅表现出很强的弹塑性特征[19-20]，材料去除特征和目前的刚塑性假设明显不符。SURATWALA等[21]针对光学玻璃抛光加工过程的模拟，提出了2种弹塑性磨削模型。一个模型认为：在磨粒切削过程中，如果作用在磨粒上的力超过一定值，磨粒就会对工件造成恒定深度的切削作用。另一个模型则认为：磨粒的实际切削深度与未变形切削深度存在一定的比例关系。考虑材料弹塑性之后的仿真结果与实验结果，在工件表面纹理、粗糙度和表面能量谱方面都有较好的吻合。因此，不论是理论分析还是实践加工，在纳米级切削深度的超精密磨削过程中，考虑工件材料的弹塑性都尤为重要。

此外，超细金刚石砂轮的磨粒多为多面体结构的微米尺度颗粒，磨粒切深在百纳米以下时，实际上只有磨粒的近似球形顶点部分参与了切削，所以对磨削后形貌有影响的是磨粒顶端部分的刃圆半径而不是磨粒整体的半径。在一些基于磨粒的划擦实验和磨削实验中也可以看到，磨痕的曲率半径和磨粒粒径有很大差异[17]。但是，对于磨粒粒径在微米量级的超细金刚石砂轮，其刃圆半径的测定和评估仍旧没有很好的方法。

在现有的磨削纹理数值仿真模型相关文献中，磨粒对工件材料均为刚性去除[4, 10]，即工件材料与磨粒接触即被去除。但是在实际磨削过程中，如果磨粒一直处在划擦阶段就不可能去除工件材料，因此有效切削磨粒的切深要大于耕犁阶段与切削阶段的临界切深，即磨粒成屑临界切深，因此有必要在磨削纹理仿真模型中考虑成屑临界切深。MATTHIAS 等[22]通过单颗CBN磨粒高速划擦实验，对磨粒成屑临界切深进行了测量。言兰等[23]通过构建划擦过程的数值仿真模型，研究了划擦速度等对成屑临界切深的影响。SON 等[24]对二维直角切削过程的切削力进行了分析，得到了刀具切深很小时进入切削状态的临界切深。

以上是针对现有工件旋转磨削仿真模型在应用于细粒度砂轮磨削过程仿真时，出现较大误差的问题提出的几点改进，这些因素目前还没有直接的实验与理论支撑，仍需要进行进一步的研究。

5 结论

为更准确地仿真磨粒切深及工件形貌，基于现有磨削仿真模型相关文献中的假设，构建了可以对磨粒平均切深及磨削区形貌进行计算的工件旋转磨削仿真模型，并使用不同粒度的砂轮进行磨削实验，验证仿真结果。总结了目前研究中存在的问题并提出了改进建议：

(1)仿真模型输出的磨粒平均切深，小于基于Hertz接触理论计算得到的磨粒进入耕犁阶段所需的最小切深；仿真模型得到的仿真区纹理特征以及粗糙度参数都与实验结果有较大偏差。改变磨削过程中的有效磨粒数，如修改磨粒体积比为原始值的1/40，则模型对粗粒度砂轮的预测较为准确；但随着砂轮粒度逐渐变细，仿真模型预测结果与实验结果也出现了较大的偏差。但此修改缺乏理论支持，即磨粒体积比最小只能降低至原始值的1/5。

(2)在超精密磨削仿真模型中，应考虑硅材料的弹塑性效应，计算磨粒顶端的刃圆半径及成屑临界切深等。

我们将进一步研究有效磨粒数修正理论及仿真参数的选取与设定，努力提高工件旋转模型预测的准确性，进而提高硅片表面的加工质量与效率。

[1] CHEN J, WOLF I. Study of damage and stress induced by back grinding in Si wafers [J]. Semicond. Sci. Tech. , 2003, 18(4): 261-268.

[2] PEI Z J, STRASBAUGH A. Fine grinding of silicon wafers [J]. Int. J. Mach. Tool. Manu. , 2001, 41(5): 659-672.

[3] ZHOU L, TIAN Y B, HUANG H, et al. A study on the diamond grinding of ultra-thin silicon wafers [J]. P. I. Mech. Eng. P-B: J. Eng. Manu. , 2012, 226(1): 66-75.

[4] CAO Y L, GUAN J Y, LI B, et al. Modeling and simulation of grinding surface topography considering wheel vibration [J]. Int. J. Adv. Manuf. Tech. , 2013, 66: 937-945.

[5] PAUL S. Numerical modeling of surface topography in super-abrasive grinding [J]. Int. J. Adv. Manuf. Tech. , 2008, 39: 29-38.

[6] GONG Y D, WANG B, WANG W S. The simulation of grinding wheels and ground surface roughness based on virtual reality technology [J]. J. Mater. Process. Tech. , 2002, 129: 123-126.

[7] LIU Y M, WARKENTIN A, BAUER R, et al. Investigation of different grain shapes and dressing to predict surface roughness in grinding using kinematic simulations [J]. Precision Engineering, 2013, 37: 758-764.

[8] CHEN X, ROWE B, MILLS B, et al. Analysis and simulation of the grinding process- Part IV: Effects of wheel wear [J]. Int. J. Mach. Tool. Manu. , 1998, 38(1-2): 41-49.

[9] ZHOU X, XI F. Modeling and predicting surface roughness of the grinding [J]. Int. J. Mach. Tool. Manu. , 2002, 42: 969-977.

[10] AHEARNE E, BYRNE G. Simulation of the local kinematics in rotational grinding [J]. CIRP Annals-Manufacturing Technology, 2008, 57: 333-336.

[11] ZHOU L B, EDA H, SHIMIZU J. State-of-the-art technologies and kinematical analysis for one-stop finishing ofφ300 mm Si wafer [J]. J. Mater. Process. Tech. , 2002, 129: 34-40.

[12] 田业冰. 大尺寸硅片磨削平整化理论与工艺技术的研究 [D]. 大连: 大连理工大学, 2007.

TIAN Yebing. Study on grinding-based flattening theory and process technology for large-sized silicon wafer [D]. Dalian: Dalian University of Technology, 2007.

[13] CHEN X, ROWE W B. Analysis and simulation of the grinding process. Part I: generation of the grinding wheel surface [J]. Int. J. Mach. Tool. Manu. , 1996, 36(8): 871-882.

[14] DARAFON A, WARKENTIN A, BAUER R. Characterization of grinding wheel topography using a white chromatic sensor [J]. Int. J. Mach. Tool. Manu. , 2013, 70: 22-31.

[15] ZHOU L B, EBINA Y, WU K, et al. Theoretical analysis on effects of grain size variation [J]. Precision Engineering, 2017, 50: 27-31.

[16] WANG D X, GE P Q, BI W B, et al. Grain trajectory and grain workpiece contact analyses for modeling of grinding force and energy partition [J]. Int. J. Mach. Tool. Manu. , 2014, 70: 2111-2123.

[17] YOUNG H T, LIAO H T, HUANG H Y. Novel method to investigate the critical depth of cut of ground silicon wafer [J]. J. Mater. Process. Tech. , 2006, 182: 157-162.

[18] BIFANO T G, DOW T A, SCATTERGOOD R O. Ductile regime grinding: a new technology for machining brittle materials [J]. J. Eng. Industry, 1991, 113(2): 184-189.

[19] YOUN S W, KANG C G. A study of nanoscratch experiments of the silicon and borosilicate in air [J]. Mater. Sci. Eng. , 2004, 384: 275-283.

[20] GASSILLOUD R, BALLIF C, GASSER P. Deformation mechanisms of silicon during nanoscratching [J]. Physica Status Solidi, 2005, 202(15): 2858-2869.

[21] SURATWALA T, FEIT M, STEELE W, et al. Microscopic removal function and the relationship between slurry particle size distribution and workpiece roughness during pad polishing [J]. J. Am. Ceram. Soc. , 2014, 97(1): 81-91.

[22] RASIM M, MATTFELD P, KLOCKE F. Analysis of the grain shape influence on the chip formation in grinding [J]. J. Mater. Process. Tech. , 2015, 226: 60-68.

[23] 言兰, 姜峰, 融亦鸣. 基于数值仿真技术的单颗磨粒切削机理 [J]. 机械工程学报, 2012, 48(11): 172-182.

YAN Lan, JIANG Feng, RONG Yiming. Grinding mechanism based on single grain cutting simulation [J]. J. Mech. Eng. , 2012, 48(11): 172-182.

[24] SON S M, LIM H S, AHN J H. The effect of vibration cutting on minimum cutting thickness [J]. Int. J. Mach. Tool. Manu. , 2006, 46: 2066-2072.