服务组合的代数规约*
2018-07-05刘冬梅何娟娟
陈 颖,刘冬梅,朱 鸿,兰 斌,何娟娟
(1.南京理工大学计算机科学与工程学院,江苏 南京 210094;2.英国Oxford Brookes大学计算与通信系,英国 牛津 OX33 1HX)
1 引言
近年来,服务计算得到越来越广泛的关注和应用[1]。面向网络、分布式、模块化的服务计算已经成为支持异构环境下分布式计算的主要途径[2]。然而,单个服务提供的功能有限,为更充分地利用已有服务,提高系统开发效率,需要将单个服务组合成更强大的服务。因此,服务组合一直是服务计算研究的热点。现有的服务组合描述方法主要基于业务流程,这些方法虽然可以有效地描述组合服务的实现方式,但缺乏对预期组合结果的功能性语义定义,从而难以支持服务组合正确性的验证和测试[3,4]。
代数规约[5]作为一种形式化方法,最早被用于描述抽象数据类型。在过去30多年中,它发展到用于描述各种软件系统,尤其是将行为代数[6]和合代数[7 - 9]理论相结合后,能够抽象地描述并发系统、基于状态系统和软件构件。在前期工作中,我们扩展了行为代数和合代数理论,提出面向服务的代数规约语言SOFIA(Service-Oriented Formalism In Algebras)[10],并开发了自动化测试工具,实现了基于SOFIA语言书写的规约对单个服务进行自动化测试[11,12]。与其他形式化方法相比,代数规约高度抽象且支持自动化软件测试[11 - 15]。
本文针对服务组合的正确性验证和测试问题,提出用代数规约描述服务组合的方法。该方法以现有服务的代数规约为基础,用代数规约形式化地、抽象地定义服务组合的实现,并进一步用代数规约定义组合服务对外提供的抽象接口和功能语义,从而形成了由实现规约和抽象规约组成的服务组合代数规约的双元结构。在双元结构的基础上,进一步定义了服务组合实现规约和抽象规约之间必须满足的“实现”关系。为了支持该方法的实现,本文扩展了面向服务代数规约语言SOFIA,提出了规约包机制,将定义一个服务系统的众多规约单元封装在一个规约包中,形成一个命名空间,增强了代数规约的重用性和可组合性。
本文第2节介绍代数规约的基本概念;第3节定义代数规约的规约包机制,讨论如何应用代数规约描述服务组合,并定义代数规约之间的实现关系;第4节结合实例介绍服务组合描述机制;第5节分析所提描述机制的一些特性;第6节讨论本研究的一些相关工作;第7节展望未来的工作。
2 软件系统的代数规约
一个面向服务的系统可以看成一组相互关联的软件实体的集合,每个软件实体可以是抽象数据类型、类、构件、服务或服务组合等,用来表示现实世界中的物理对象、设备、数据、抽象概念或商业过程等[10]。在面向服务系统的代数规约中,每个软件实体可以用一个规约单元来描述,规约单元也称为类子。类子之间有使用和扩展两种关系,类似于面向对象中的关联和继承关系,记为≻和▷。通过这两种关系可从已有规约单元构造新的规约单元。一个结构良好的代数规约将系统中每个软件单元及相关概念和实体都抽象为相应的规约单元,并且实体之间的关系对应成规约单元之间的关系。
2.1 代数规约的基调
定义1(系统基调(System Signature)) 软件系统的基调由有序对(S,Σ)表示,其中,
(1)S=(St,≻,▷),其中St是类子的有限集;≻是集合St上的使用关系,s1≻s2表示类子s1使用类子s2;▷是集合St上的扩展关系,s1▷s2表示类子s1扩展类子s2。
(2)Σ={Σs|s∈St}是所有单元基调Σs的集合。

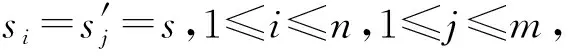
2.2 代数规约的公理
令(S,Σ)为系统基调,定义Vs为类型为s的变量集,其中s∈St。假设ss1,s2,…,sn,s′,其中ss′表示s≻s′或s=s′。
定义3(s-项(s-term)) 类子s的项记为s-项,其递归定义如下:
(1)类型为w的s′-项τ是类型为w的s-项;
(2)对所有v∈Vs′,v是类型为s′的s-项;
(3)对所有类型为s1,…,sn的s-项τ1,…,τn,〈τ1,…,τn〉是类型为(s1,…,sn)的s-项;
(4)对所有类型为(s1,…,sn)的s-项τ,τ#i,1≤i≤n,是类型为si的s-项;
(5)对所有φs:w→w′,φ(τ)是类型为w′的s-项,其中τ是类型为w的s-项。
定义4(等式(Equation)) 条件等式e是一个三元组(τ,τ′,C),其中τ和τ′是类型相同的s-项,C={(ci,di)|0≤i≤n}是条件集合,其中当i=0,1,…,n时,ci和di为类型相同的s-项。条件等式e=(τ,τ′,C)可以表示为(τ=τ′,C),其语义是当C中所有条件ci=di(0≤i≤n)成立时,有τ=τ′。
定义5(公理集(Axiom Set)) 定义类子s上的公理集Axs是s中公理ax的有限集,公理ax是二元组(V,e),e为条件等式,V={vs′|ss′},vs′是公理e中的类型为s′的变量,集合V可为空。
定义6(系统规约(System Specification)) 系统规约用三元组(S,Σ,Ax)表示,其中(S,Σ)是系统基调,Ax={Axs|s∈St}是公理集Axs的有限集。
为提高代数规约的模块化特性,在使用代数规约语言时,系统规约往往分解成一组规约单元,规约单元定义如下:
定义7(规约单元(Specification Unit)) 类子sn的规约单元是一个三元组(s,Σsn,Axsn),其中,
(1)s=(sn,sn≻,sn▷),sn是规约单元名,也称类子名,sn≻是sn上的使用关系集合;sn▷是sn上的扩展关系集合;
(2)Σsn是类子sn的单元基调;
(3)Axsn是定义在类子sn上的有限公理集。
2.3 代数规约的语义
定义8(代数(Algebra)) 给定系统基调(S,Σ),一个(S,Σ)代数A表示为(A,F),其中,
(1)A={As|s∈St}是由s索引的载体集As组成的有限集;
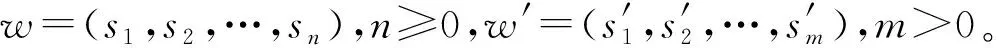
定义9(代数中项的值(Evaluation of Terms in an Algebra)) 将项中的变量映射到A的赋值函数记为α。给定一个赋值函数α,(S,Σ)-代数A=(A,F)中项τ的值记作Evaα(τ),其定义如下:
(1)Evaα(v)=α(v);
(2)Evaα(〈τ1,…,τn〉)=〈Evaα(τ1),…,Evaα(τn)〉;
(3)Evaα(τ#i)=ai,如果Evaα(τ)=〈a1,…,an〉,1≤i≤n;
(4)Evaα(φ(τ))=fA,φ(Evaα(τ))。
定义10(满足性(Satisfaction)) 令ax是公理(V,e),e为条件等式τ=τ′,C,其中C={(ci,di)|0≤i≤n}。若对所有V的赋值函数α,当Evaα(ci)=Evaα(di),i=1,2,…,n成立时,有Evaα(τ)=Evaα(τ′),则称(S,Σ)-代数A=(A,F)满足公理ax,记为A|=ax。令规约ε=(S,Σ,Ax),若(S,Σ)-代数A=(A,F)满足Ax中所有公理ax,则称代数A满足规约ε,记作A|=ε。
3 服务组合的代数规约方法
本节讨论如何应用代数规约方法描述服务的组合。首先引入“规约包”的概念,将一个服务的规约封装在一个包中,以便对服务进行组合。
3.1 规约包
一个系统的代数规约通常包含许多规约单元,给人们书写和理解规约带来不便,也为代数规约的重用和组合带来不便。为此,本文提出规约包机制,将面向服务系统的代数规约拆分封装成若干个包,将关系较为密切的类子放在同一包中。一个包可以引用其他包。通过引用其它包,包中类子可以使用被引用包中的类子。令P、Q为两个包,用P≻Q表示包P引用包Q。包机制有以下特点:
(1) 同一包中的类子名不同,不同包中的类子名可以相同,因此包可以避免类子命名冲突;
(2) 关系紧密的类子放在同一包中,进一步增强了代数规约模块化特性;
(3) 通过引用其他包,可以提高代数规约的重用性。
假设面向服务系统的代数规约是规约单元集合{U1,…,Un},n>0,将关系密切的规约单元构建为一个包,则系统规约划分为包集合{P1,…,Pl},l>0,且
①对于任意Pi,1≤i≤l,Pi≠∅;

③Pi∩Pj=∅;
④若Pj≻Pi,则允许Ub≻Ua,其中Ub∈Pj,Ua∈Pi。
一个包P由一系列规约单元U1,…,Uk组成,有一个唯一的名称IdP,并给出所引用的包P1,…,Pn的名称IdP1,…,IdPn。即包是一个三元组P=(IdP,{IdP1,…,IdPn},{U1,…,Uk})。
定义11(包的语义(Semantics of Package)) 包P=(IdP,{IdP1,…,IdPn},{U1,…,Uk})的语义是一个规约(SP,ΣP,AxP),其定义如下:
如果包P不引用任何其它包,即P=(IdP,{},{U1,…,Uk}),则:
(1)SP=({s1,…,sk},≻P,▷P),si是规约单元Ui的类子名,≻P和▷P分别是规约单元U1,…,Uk之间的使用和扩展关系;
(2)ΣP={Σs|s∈{s1,…,sk}};
(3)AxP={Axs|s∈{s1,…,sk}}。
如果包P引用P1,…,Pn,n>0,令(Si,Σi,Axi)为包Pi所定义的规约,则:
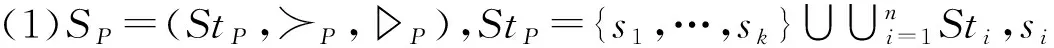
□
假定服务CS需要通过其他调用服务S1,…,Sn(n>1)以实现其功能,即CS是由服务S1,…,Sn组合而成。服务CS可以用两种不同的代数规约来定义:
(1)用代数规约抽象地定义服务的用户接口和功能,称这样的代数规约为服务的抽象规约;
(2)用代数规约定义该服务由哪些其他服务组成,描述每个向用户提供的服务如何转化为对其他服务的调用等实现方式,如同用代数规约描述如何用已有的数据类型实现新的数据类型,称这样的代数规约为服务的实现规约。
服务组合的抽象规约描述服务组合所提供的抽象功能,描述用户对所期待服务的功能需求,不涉及服务组合的具体实现细节,而服务组合的实现规约则描述组合服务CS如何调用其他服务S1,…,Sn来实现其功能。由此可见,一个完整的服务组合代数规约应该包含三个层次:组合抽象层、组合实现层和被调用服务层。
规约语言的包机制可以有效地支持这样的规约结构。如图1所示,可以将被调用服务的代数规约放在相应包中,组合服务的抽象规约放在一个包(或几个包)中,组合服务的实现规约放在另一个(或几个包中)且申明引用被调用服务规约的包。图1中包PIMP为组合服务CS的实现规约,被调用服务S1,…,Sn的代数规约分别定义在包PS1,…,PSn中,且PIMP≻PS1,…,PSn,组合服务CS的抽象规约定义在包PABS中。
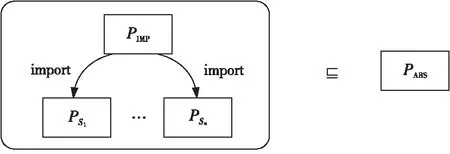
Figure 1 Algebraic specifications of web service composition图1 服务组合代数规约的结构
由包的语义定义可知,抽象规约包PABS相当于一个系统规约(ABS,ΣABS,AxABS),其中,
(1)ABS=〈Abs,Abs≻,Abs▷〉,Abs是抽象组合服务类子的集合,Abs≻和Abs▷分别表示Abs上的使用和扩展关系;
(2)基调ΣABS描述组合服务的抽象接口;
(3)公理集AxABS描述ΣABS中服务操作的语义,需要注意的是,AxABS中的公理并不描述组合服务如何调用其他服务,而是将组合服务看成一个原子服务,描述其应当满足的特性。
实现规约包也是一个系统规约三元组(IMP,ΣIMP,AxIMP),其中,
(1)IMP=〈Imp,Imp≻,Imp▷〉,Imp是组合实现中所涉及的类子名的集合,Imp≻和Imp▷为这些类子的使用和扩展关系。对于一个正确的实现规约,要求Abs⊆Imp,并且如果类子s是一个被组合的服务,s∈Imp。
(2)ΣIMP是所实现服务的接口。作为一个正确的实现,要求抽象规约中定义的服务操作都被实现了,即ΣABS⊆ΣIMP。
(3)公理集AxIMP中公理ax=(V,e),描述如何通过调用其他服务来实现所需的服务操作。如果这些公理所描述的实现是正确的,那么应该能保证那些在抽象规约中定义服务需求的公理是成立的。因此,要求能够从这些公理以及被组合的服务规约公理推导出抽象规约中的公理。
根据如上分析,下一节定义代数规约之间的实现关系。
3.2 代数规约之间的实现关系
定义12(实现关系(Implementation Relation)) 令CSIMP=(S,Σ,Ax)和CSABS=(S′,Σ′,Ax′)分别为两个代数系统规约。CSIMP是CSABS的正确实现,表示为CSIMP⊆CSABS,如果下述三个条件成立:
(1)St′⊆St;
(2)Σ′⊆Σ;
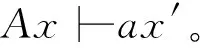
上述定义中,条件(1)要求所有在抽象规约中定义的软件实体都在实现规约中实现了,条件(2)要求抽象规约中的操作都在实现规约中实现了,条件(3)要求抽象规约所具有的服务特性都被实现规约满足了。因此,CSIMP正确地实现了CSABS所规约的系统。
定义13(模型(Model)) 给定代数系统规约ε=(S,Σ,Ax),一个代数A是(S,Σ,Ax)的模型,如果A存在一个子代数A′满足条件:(1)A′是一个(S,Σ)代数;(2)A′|=ε,即A′满足公理Ax。用Mod(ε)表示规约ε的模型的集合。
由模型的概念及代数规约的语义定义易证明下面的定理为真,证明从略.

定理1说明,如果一个组合服务系统满足实现规约且实现规约相对于抽象规约是正确的,那么该组合服务系统一定满足抽象规约,也就是一个相对于抽象规约的正确实现。
4 实例
本节以订票组合服务TravelS为例,说明用代数规约语言SOFIA描述组合服务的方法。
该服务根据服务请求中包含的雇员信息和旅行信息,返回机票价格较低的订票信息。它由如下服务组合而成:(1)雇员状态服务EmployeeInfoS,根据雇员的姓名和员工号,提供雇员的职位等基本信息,并提供雇员所允许的旅行仓位(如经济舱、商务舱或头等舱等);(2)美国航空公司和达美航空公司提供的机票查询服务AAFlightTicketS和DAFlightTicketS。订票组合服务TravelS比较两者的机票价格,返回适合旅行者身份的价格较低的订票信息。
4.1 代数规约的总体结构
三个被组合服务EmployeeInfoS、AAFlightTicketS、DAFlightTicketS的代数规约分别封装在三个包中,组合服务的实现规约和抽象规约分别封装在TravelSImp包和TravelS包中。此外,包AirTravel包含了机票服务有关的公共概念。包之间的引用关系如图2所示。

Figure 2 Algebraic specifications of TravelS图2 订票组合服务代数规约的结构
4.2 被组合服务的规约
下面是AAFlightTicketS的代数规约。
package AAFlightTicketS;
import AirTravel;
spec AAFlightTicketS;
uses TravelClass,FlightReq,Flight;
operation
ticketReq(TravelClass,FlightReq):Flight;
axiom
for allaa:AAFlightTicketS,tc:travelClass,f:FlightReq that
aa.ticketReq(tc,f).class=tc;
(1)
aa.ticketReq(tc,f).leavingFrom=f.leavingFrom;
aa.ticketReq(tc,f).destination=f.destination;
aa.ticketReq(tc,f).departDateTime.date=f.departDate;
(2)
aa.ticketReq(tc,f).returnDateTime.date=f.returnDate;
end
end
end
DAFlightTicketS的规约包类似,故省略。因篇幅限制,也略去EmployeeInfoS和AirTravel规约包的细节。
4.3 服务组合的抽象规约
订票服务的抽象规约如下:
package TravelS;
import EmployeeInfoS,AAFlightTicketS,DAFlightTicketS;
spec TravelS;
uses Employee,FlightReq,Flight,EmployeeInfoS,AAFlightTicketS,DAFlightTicketS;
operation
travelReq(Employee,FlightReq):Flight;
axiom
for alle:Employee,f:FlightReq,ts:TravelS,es:EmployeeInfoS,aa:AAFlightTicketS,da:DAFlightTicketS
that
ts.travelReq(e,f).departDateTime.date=f.departDate;
(3)
ts.travelReq(e,f).returnDateTime.date=f.returnDate;
(4)
ts.travelReq(e,f).destination=f.destination;
(5)
ts.travelReq(e,f).leavingFrom=f.leavingFrom;
(6)
letc=es.empInfoReq(e) in
ts.travelReq(e,f).class=c;
(7)
ts.travelReq(e,f).price=min(aa.ticketReq(c,f).price,da.ticketReq(c,f).price);
(8)
end
end
end
end
订票服务抽象规约单元TravelS定义了一个服务操作travelReq,用户提供员工信息和旅行信息,服务返回与员工身份相符的旅行机票信息。公理(3)~公理(6)要求服务提供的机票信息的出发日期、返回日期、目的地和出发地与服务请求中的相应信息是吻合的。公理(7)要求服务返回的机票的等级与旅行者的身份一致。公理(8)要求机票的价格是两家航空公司相应票价中的较低者。
4.4 组合实现的规约
订票服务的实现规约如下:
package TravelSImp;
import EmployeeInfoS,AAFlightTicketS,DAFlightTicketS;
spec TravelS;
uses Employee,FlightReq,Flight,EmployeeInfoS,AAFlightTicketS,DAFlightTicketS;
attr
empInfoS:EmployeeInfoS;
aaTicketS:AAFlightTicketS;
daTicketS:DAFlightTicketS;
operation
travelReq(Employee,FlightReq):Flight;
axiom
for allts:TravelS,e:Employee,f:FlightReq that
let
c=ts.empInfoS.empInfoReq(e);
aaTicket=ts.aaTicketS.ticketReq(c,f);
(9)
daTicket=ts.daTicketS.ticketReq(c,f);
in
ts.travelReq(e,f)=aaTicket,ifaaTicket.price (10) ts.travelReq(e,f)=daTicket,ifaaTicket.price>=daTicket.price; (11) end end end end 上述规约说明TravelS包含三个服务作为其成分:empInfoS是EmployeeInfoS服务,aaTicketS是AAFlightTicketS服务,daTicketS是DAFlightTicketS。其中公理(10)规定当AAFlightTicketS服务返回的票价低于DAFlightTicketS服务返回的票价时,选择美联航空公司的机票。公理(11)规定当AAFlightTicketS服务返回的票价等于或高于DAFlightTicketS服务返回的票价时,选择达美航空公司的机票。值得注意的是,抽象规约没有指定当两家航空公司的票价一样时选择哪个。因此,实现规约和抽象规约并不完全一样。 本节证明TravelS的实现规约正确实现了其抽象规约。首先,TravelS规约包的类子集合与TravelSImp包的类子集合完全相同。其次,TravelS在抽象规约包TravelS中说明的操作是在TravelSImp规约包中说明的操作的子集,这是因为在TravelSImp规约包中比TravelS包中多了三个观察操作:empInfoS:EmployeeInfoS,aaTicketS:AAFlightTicketS,daTicketS:DAFlightTicketS。因此,实现关系的条件(1)和(2)均满足。下面证明条件(3)也满足。 (1)证明抽象规约包TravelS中的公理(3)成立。 由实现规约包TravelSImp中的公理(9)和公理(10)可知,当aaTicket.price ts.travelReq(e,f).departDateTime.date=aaTicket.departDateTime.date=ts.aaTicketS.ticketReq(c,f).departDateTime.date 又由被调用服务类子AAFlightTicketS中公理(2)可知 ts.travelReq(e,f).departDateTime.date=ts.aaTicketS.ticketReq(c,f).departDateTime.date=f.departDate 同理可证,当aaTicket.price>=daTicket.price时,有: ts.travelReq(e,f).deparDateTime.date=ts.daTicketS.ticketReq(c,f).departDateTime.date=f.departDate 因此,TravelS包中的公理(3)成立。 类似地,可以证明抽象规约包中的公理(4)~公理(6)成立。 (2)证明抽象规约包TravelS中的公理(7)成立。 由实现规约包TravelSImp的公理(9)和公理(10)可知,当aaTicket.price ts.travelReq(e,f).class=aaTicket.class=ts.aaTicketS.ticketReq(c,f).class 其中c=ts.empInfoS.empInfoReq(e)。 又由AAFlightTicketS规约中的公理(1)可知 ts.travelReq(e,f).class=ts.aaTicketS.ticketReq(c,f).class=c 同理可证,当aaTicket.price>=daTicket.price时,有 ts.travelReq(e,f).class=ts.daTicketS.ticketReq(c,f).class=c 因此,抽象规约包TravelS中的公理(7)成立。 (3)证明抽象规约包TravelS中的公理(8)成立。 由实现规约包TravelSImp中的公理(9)和公理(10)可知,当aaTicket.price ts.travelReq(e,f).price=aaTicket.price=ts.aaTicketS.ticketReq(c,f).price 当aaTicket.price>=daTicket.price时,有 ts.travelReq(e,f).price=daTicket.price=ts.daTicketS.ticketReq(c,f).price 因此,抽象规约包TravelS中的公理(8)成立。 综合上述结果,由定义12,TravelSImp是TravelS的一个正确实现。 □ 本文提出的服务组合的代数规约方法具有如下特性。 (1)抽象性:SOFIA作为一种代数规约语言,将服务系统中的实体都抽象为规约单元。在描述服务组合时,既可以给出组合服务的抽象描述,也可以描述其组合的实现。由于语言的抽象化特点,调用其他组合服务时,往往只需考虑被调用服务的抽象接口,而不用考虑多层组合服务的嵌套。 (2)表达力:服务组合中,多个被调用服务之间的调用关系可能是顺序、选择或者循环调用,其中循环组合可由递归等式描述。SOFIA语言书写顺序和选择服务调用的公理形式如下。 ①顺序组合。 顺序组合是指多个服务按顺序依次执行,前一个服务的输出结果作为后一个服务的输入参数。假定φ是组合服务CS的一个操作,其输入的类子为R。如果服务操作φ的实现是依次调用服务sa的操作φ1和服务sb中的操作φ2,则公理的形式如下: For allsc:CS,x:R that sc.(x)=sc.sb.(sc.sa.(x)); End ②选择组合。 如果组合服务的操作φ根据条件选择要执行的服务,例如当条件Con为真时,调用服务sa中操作φ1,否则调用服务sb中操作φ2,则公理的形式如下: For allsc:SC,r:R that sc.φ(r)=sc.sa.φ1(r),if Con; sc.φ(r)=sc.sb.φ2(r),if not Con; End (3)可验证性:若组合服务的抽象规约单元中的公理能够由被调用服务规约的公理和组合实现规约中的公理证明得到,那么组合实现是正确的。上述订购机票组合服务的例子说明,这样的证明是可行的。 目前,Web服务组合规范主要从工作流程的角度描述和定义参与服务组合的各个子服务之间的动态交互的逻辑顺序,工业界广泛采用的业务流程执行规范BPEL(Business Process Execution Language)将服务组合调用动作视为一组活动,用控制流块结构组织这些活动,并提供服务组合的抽象行为和具体实现描述[16],但这种方法缺乏形式化语义以及验证机制来保证服务组合的质量[17]。针对服务组合的可验证性和可测试性这一问题,学者们基于Web服务组合规范建立形式化模型,以形式化方法定义和描述服务组合的各个子服务之间的动态交互,其中使用最多的三种形式化方法分别是有限自动机及其变体[18,19]、Petri网[20,21]和进程代数[22]。这些已有工作主要对服务和服务之间的交互行为建模,并支持组合的性质如死锁避免、数据类型一致性和动态行为匹配性的检查和验证。但是,这些方法着重关注服务组合调用行为的协调性,缺乏对服务功能的描述,因此难以支持对服务功能正确性的验证和测试。 与上述三种形式化方法相比,代数规约[5]不仅能够描述软件行为,还能通过公理描述软件功能。代数规约作为一种高度抽象的形式化方法,从20世纪70年代被提出发展至今,其理论基础从初始代数发展到终代数、行为代数[7]和合代数[7 - 9],描述对象从抽象数据类型扩展到并发系统、基于状态的系统和软件组件。在前期工作中,我们扩展了行为代数和合代数理论,提出设计并实现了面向服务系统的代数规约语言SOFIA[10]。对服务系统代数规约的实例研究表明,与其他形式化方法相比,代数规约具有表达力强、高度模块化等特点,更适合描述服务系统[11 - 15],但文献中尚未见将代数规约技术用于描述服务组合的研究。本文在上述研究的基础上,将包的概念引入到代数规约语言,进一步扩展了SOFIA语言,提高服务描述的模块化特性,从而支持服务描述的重用和组合。包作为一个软件语言设施已广泛应用于程序设计语言,但未见于代数规约语言。本文定义的代数规约之间的实现关系与传统代数规约理论中的定义有所不同,传统的定义要求两个代数规约的基调完全相同[23]。但是,我们在描述组合服务的实例研究中发现,如同本文的例子所示,抽象规约和实现规约的基调可能不同,实现规约的基调可能包含额外的用于实现组合的操作,并可能使用抽象规约中无需指定的类子。相应地,我们对规约的模型概念也作了修改。在定理1中我们证明了,对这些代数规约基本概念的修改保持了“实现规约的模型必须也是抽象规约的模型”这个重要性质。本文给出的例子说明,证明实现规约与抽象规约之间的实现关系是可行的,为形式化验证和测试服务组合描述的正确性奠定了基础。 代数规约方法的一个主要特点是支持软件测试的自动化,包括测试用例生成,测试执行和测试结果正确性判断,代表性的研究成果有:Bernot等[24]开发的测试过程程序的测试工具。针对面向对象软件,Doong等[25]提出LOBAS规约语言并开发自动化测试工具ASTOOT,Hughe等[26]开发了DAISTISH。针对Java平台软件组件,Zhu等[14,15]提出CASOCC语言并开发CASCAT自动化测试工具。在前期工作中,我们设计并实现了以代数规约语言SOFIA为基础的自动化测试工具,支持对单个服务进行自动化测试[11,12]。此外还提出了代数规约到语义本体的转换方法[27],并开发了转换工具TrS2O[28],将服务的代数规约转换成本体语义描述,使得代数规约在机器可理解性和人工可读性方面得到改善。 本文提出了基于代数规约的服务组合形式化规约方法,使验证和测试服务组合的正确性成为可能。下一步的工作将进一步进行实例研究,总结服务组合的模式,设计并实现证明服务组合正确性的自动化推导工具,以及服务组合自动测试工具。 [1] Papazoglou M P,Heuvel W J.Service oriented architectures:Approaches,technologies and research issues[J].The VLDB Journal—The International Journal on Very Large Data Bases,2007,16(3):389-415. [2] Bouguettaya A, Sheng Q Z, Daniel F.Web services foundations[M].New York:Springer,2014. [3] Goguen J A,Thatcher J W,Wagner E G,et al.Initial algebra semantics and continuous algebras[J].Journal of the ACM (JACM),1977,24(1):68-95. [4] Bartalos P,Bieliková M.Automatic dynamic web service composition:A survey and problem formalization[J].Computing and Informatics,2012,30(4):793-827. [5] Charif Y,Sabouret N.An overview of semantic web services composition approaches[J].Electronic Notes in Theoretical Computer Science,2006,146(1):33-41. [6] Goguen J,Malcolm G.A hidden agenda[J].Theoretical Computer Science,2000,245(1):55-101. [7] Cirstea C.Coalgebra semantics for hidden algebra:Parameterised objects and inheritance[C]∥Proc of International Workshop on Algebraic Development Techniques,1997:174-189. [8] Rutten J J M M.Universal coalgebra:A theory of systems[J].Theoretical Computer Science,2000,249(1):3-80. [9] Bonchi F,Montanari U.A coalgebraic theory of reactive systems[J].Electronic Notes in Theoretical Computer Science,2008,209:201-215. [10] Liu D,Zhu H,Bayley I.SOFIA:An algebraic specification language for developing services[C]∥Proc of 2014 IEEE 8th International Symposium on Service Oriented System Engineering (SOSE),2014:70-75. [11] Liu D,Liu Y,Zhang X,et al.Automated testing of web services based on algebraic specifications[C]∥Proc of the International Workshop on Service-Oriented System Engineering,2015:143-152. [12] Liu D,Wu X,Zhang X,et al.Monic testing of web services based on algebraic specifications[C]∥Proc of Service-Oriented System Engineering (SOSE),2016:24-33. [13] Chen H Y,Tse T H,Chen T Y.TACCLE:A methodology for object-oriented software testing at the class and cluster levels[J].ACM Transactions on Software Engineering and Methodology (TOSEM),2001,10(1):56-109. [14] Kong L,Zhu H,Zhou B.Automated testing EJB components based on algebraic specifications[C]∥Proc of the 31st Annual International Computer Software and Applications Conference(COMPSAC 2007),2007:717-722. [15] Yu B, Kong L,Zhang Y,et al.Testing java components based on algebraic specifications[C]∥Proc of 2008 1st International Conference on Software Testing,Verification,and Validation,2008:190-199. [16] Weske M.Business process management architectures[M]∥Business Process Management.Berlin:Springer Berlin Heidelberg,2012:333-371. [17] Aalst W M P V D,Dumas M,Hofstede A H M T.Web service composition languages:Old wine in new bottles?[C]∥Proc of the 29th Conference on Euromicro,2003:298-305. [18] Keum C S,Kang S,Ko I Y,et al.Generating test cases for web services using extended finite state machine[C]∥Proc of the 18th International Conference on Testing of Communicating Systems,2006:103-117. [19] Ramollari E,Kourtesis D,Dranidis D,et al.Leveraging semantic web service descriptions for validation by automated functional testing[C]∥Proc of European Semantic Web Conference on the Semantic Web:Research and Applications,2009:593-607. [20] Zhu H,He X.A methodology of testing high-level Petri nets[J].Information & Software Technology,2002,44(8):473-489. [21] Xu D.A tool for automated test code generation from high-level Petri nets[C]∥Proc of International Conference on Applications and Theory of Petri Nets-,2011:308-317. [22] Frantzen L, Huerta M D L N, Kis Z D,et al.On-the-fly model-based testing of web services with Jambition[C]∥Proc of Web Services and Formal Methods,2009:143-157. [23] Sannella D,Tarlecki A.Foundations of algebraic specification and formal software development[M].Berlin:Springer,2012. [24] Bernot G,Gaudel M C,Marre B.Software testing based on formal specifications:A theory and a tool[J].Software Engineering Journal,2010,6(6):387-405. [25] Doong R K,Frankl P G.The ASTOOT approach to testing object-oriented programs[J].ACM Transactions on Software Engineering and Methodology(TOSEM),1994,32(2):101-130. [26] Hughes M,Stotts D.Daistish:Systematic algebraic testing for OO programs in the presence of side-effects[C]∥Proc of the 1996 ACM SIGSOFT International Symposium on Software Testing and Analysis,1996:53-61. [27] Liu D,Zhu H,Bayley I.From algebraic specification to ontological description of service semantics[C]∥Proc of IEEE,International Conference on Web Services,2013:579-586. [28] Liu D,Zhu H,Bayley I.Transformation of algebraic specifications into ontological semantic descriptions of web services[J].International Journal of Services Computing,2014,2(1):58-71.4.5 证明实现关系
5 讨论
6 相关工作
7 结束语
