一种改进的模糊连接点聚类算法*

孙明珊，覃 华，苏一丹

(广西大学计算机与电子信息学院，广西 南宁 530004)

1 引言

模糊聚类是一类建立在模糊数学基础上的数据挖掘方法[1]，其中较为经典的是模糊C均值聚类算法FCM(Fuzzy C-means)[2]，它把聚类问题转化为对一个最优化问题的求解从而实现对数据集的模糊划分，目前FCM已被广泛应用于电力系统[3]、环境科学[4]、空间图像处理[5]、医疗[6]、电子与信息工程[7,8]等领域。FCM聚类前需要先确定簇的数目，但很多实际工程问题中，聚类前并不知道数据集中簇的个数，为解决此问题，文献[9,10]用粒子群PSO(Particle Swarm Optimization)产生初始聚类中心，获取簇的数目，最后再用FCM进行聚类，但PSO本质上属于随机搜索算法，每次运算得到的簇数目不尽相同，影响了FCM聚类的可靠性和准确性。为了解决FCM在自动模糊聚类上遇到的难题，Nasibov等人[11 - 15]另辟蹊径，提出一种新的自动模糊聚类算法—模糊连接点FJP(Fuzzy Joint Points)聚类算法，它的基本思想是：对于给定的数据集X，先用距离公式计算X的模糊相似度矩阵T，再用最大-最小合成法为T构造一个传递闭包(Transitive Closure)矩阵T*，最后在T*上用alpha扫描子算法(alpha-scan)进行聚类划分。FJP算法在聚类时之所以不需要事先知道簇的数目，是因为传递闭包T*具有传递性，描述样本数据间是否存在关联，存在关联的样本数据在FJP算法中称为模糊连接点，FJP算法利用T*的传递性判断两个样本数据是否属于同一簇。FJP算法有两个问题：首先，因其采用循环遍历相似度矩阵计算传递闭包，时间复杂度是O(n3),所以处理大数据集时计算时间较长；其次，它的相似度矩阵由欧氏距离获得，在此基础上获得的传递闭包会存在数据间关联、依赖失真的问题，从而影响FJP算法簇数目的正确性和聚类的精度[16]。

文献[17]研究了一种最优传递闭包生成算法，它采用基于核函数的桥元素填充法生成传递闭包，传递闭包失真度小，且时间复杂度只有O(n2)。本文提出用该理论为FJP算法生成传递闭包，改进FJP算法的计算效率和聚类精度，从而形成一种改进的模糊连接点聚类IFJP(Improved Fuzzy Joint Point)算法，所提算法的基本思想是：先用组合核函数生成数据集的模糊相似度矩阵，并用大顶堆存储，初始时传递闭包矩阵为空；然后遍历传递闭包矩阵的空元素，取出堆顶中的桥元素填充到传递闭包相应的空元素位置上，直至传递闭包中所有空元素被桥元素填充完毕。用此方法生成传递闭包的计算时间复杂度是O(n2)，优于传统FJP算法的O(n3)。测试数据集上的实验结果表明，本文所提算法在平均聚类准确度上较FJP-2008算法[14]提高26.7%，较FJP-2016算法[15]提高25.1%；在平均计算效率上，本文算法较FJP-2008算法提高44.5%，较FJP-2016算法提高35.5%，说明了本文用基于核函数的桥元素填充法改进FJP算法的思路是可行的、有效的。

2 用桥元素填充法生成传递闭包

原FJP算法不断遍历扫描相似度矩阵T中的每个元素，并对每个元素进行最大-最小值合成运算，更新相似度矩阵，直至矩阵各个元素不再变化即得其传递闭包T*。为避免不断遍历导致计算时间长的问题，本文采用桥元素填充法生成传递闭包，对于给定数据集X的模糊相似度矩阵T，用大顶堆数据结构存储T，依次遍历堆顶的桥元素，并把它填充到T*的空元素位置上，同时也避免了原FJP算法中多次最大-最小值合成运算，提高了计算效率。本文所用的传递闭包生成子算法如下：

输入:数据集X={x1,x2,x3,…,xn}，X的模糊相似度矩阵T。

输出:T的传递包T*。

Step1初始化一个n×n的空矩阵T*。

Step2为T构建大顶堆H。

Step3使得T*(i,i)=1,1≤i≤n。

Step4当T*中还存在空元素时，取H中的堆顶元素T(u,v)，1≤u≤n且1≤v≤n。

Step4.1若T*(u,v)为空，则T(u,v)为桥元素，I={j|T*(u,j) ≠null}且I″={i|T*(i,v) ≠null}，使T*(s,t)=T*(t,s)=T(u,v),s∈I且t∈I〃。

Step4.2删除H的堆顶元素，用文献[18]的算法重新排序堆H，产生新的堆顶元素。

上述子算法的一些关键细节说明如下。

2.1 桥元素填充传闭包规则

令P是一个n1×n1的模糊矩阵,Q是一个n2×n2的模糊矩阵，E是一个(n1+n2)×(n1+n2)的模糊矩阵，让P和Q成为模糊矩阵E左上角和右下角的子矩阵。如式(1)中，b为桥元素，其中0≤b≤min(min(P),min(Q))。若P和Q均是模糊等价矩阵，则填入桥元素构成的矩阵E,因仍然满足每个元素均大于或等于与自身同行同列元素对中较小值序列的最大值，故也是模糊等价矩阵。由Step 4知，当前T*中已填充的元素通过行列置换构成对角分块矩阵，两个对角分块矩阵均是模糊等价矩阵。当前堆顶元素小于T*中所有已填充元素，因此可作为T*已填充元素的桥元素。又因为具有最大-最小传递性的模糊矩阵即为模糊等价矩阵，则通过桥元素的添加进行模糊等价矩阵扩展，所得矩阵仍然是模糊等价矩阵。

(1)

用桥元素填充传递闭包的规则为：获得堆顶元素在T的行列数为u、v，I由T*中与堆顶元素同行元素的列下标组成，I″由T*中与堆顶元素同列元素的行下标组成，若T*中第u行v列不为空，则该堆顶元素不能称为桥元素，否则依次将I和I″中元素组成行列对在T*相应位置进行填充。

2.2 传递闭包生成子算法的计算时间复杂度

Step 4步骤是整个传递闭包生成子算法的核心，是一个循环嵌套结构，它的作用是遍历T*中的空元素，并从大顶堆H中取出堆顶桥元素填充到T*空元素位置上；如果数据集X有n个数据样本，则传递闭包T*中元素总数为n×n个，遍历T*中空元素的计算时间复杂度为O(n2)。Step 4的内部主要有Step 4.1和Step 4.2计算步骤，其中Step 4.1的计算时间复杂度是一个常量O(1)，而Step 4.2堆排序的计算时间复杂度也是一个常量O(1)[18],故整个传递闭包生成子算法的计算时间复杂度为O(n2)，较原FJP算法的传递闭包子算法的计算复杂度O(n3)有明显改善。所以，本文采用桥元素填充法生成传递闭包有利于提高整个FJP算法的计算效率，更适用于处理大数据集。

3 改进的FJP算法流程

本文所提的IFJP算法流程如下：

输入:数据集X={x1,x2,x3,…,xn}。

输出:聚类划分{C1,C2,C3,…,Ck}。

Step1参数初始化，划分水平初始值α0=max(T*)。

Step2计算模糊相似度矩阵T。

Step3调用第2节子算法生成传递闭包T*。

Step4用T*计算α划分水平的间距△α。

(2)

Step5当α0>0时，α0=α0-△α:

Step5.1S=X;k=1。

Step5.2对任意元素xi∈S，依次取S中其余所有元素xj,形成数据集Ck={xj∈S|T*(i,j)≥α0},S=SCk。

Step5.3若S非空，则k=k+1并转至Step 5.2；否则，转至Step 5.4。

Step5.4得划分数据集{C1,C2,C3,…,Ck}和划分簇数目k。

Step6出现次数最多且划分水平最小的k为划分簇数，返回结果{C1,C2,C3,…,Ck}。

上述子算法的一些关键细节说明如下。

3.1 数据样本划分水平的设置

模糊聚类理论中，已知相似度矩阵T的传递闭包T*，对给定的α划分水平，若T*(i,j)≥α，则认为样本xi和xj可划分在同一簇内。当α=1时，表示所有数据样本各自独立成一簇；而当α=0时，表示所有数据样本只分为一类。为避免遍历过多的划分水平，本文把划分水平从值域[min(T*),max(T*)]，每间隔△α制作一个分割点，得到一组划分水平{α1,α2,…,αi,…,αz}。将T*在z个不同的划分水平下分别聚类，根据z个聚类结果找出出现次数最多的簇数目并记为v，将v所对应的划分水平的最小值记为αmin。T*在αmin划分水平下的聚类结果即为最佳聚类结果，所获得的簇记为{C1,C2,C3,…,Ck}。

3.2 模糊相似度矩阵的计算

数据样本集X记为X={x1,x2,x3,…,xn}，其中n为数据样本的总数；xi∈Rm，m为样本的维度。

数据集X的模糊相似度矩阵T是一个n×n的矩阵，矩阵中的元素T(i,j)表示样本xi和xj的相似程度，常用欧氏距离函数来计算T(i,j)。为提高对复杂特征数据相似性的判别能力，本文采用文献[19]支持向量机高斯核、线性核的组合核函数来计算T(i,j)，得到数据样本集X的模糊相似度矩阵T。所用的高斯核函数为：

(3)

所用的线性核函数为:

(4)

其中,d(xi,xj)为xi和xj的欧氏距离，dmax为各数据样本间欧氏距离的最大值。由此构建X的模糊相似度矩阵T为：

T(i,j)=(1-γ)·K1(xi,xj)+γ·K2(xi,xj)

(5)

其中,γ为核函数组合系数，用文献[19]的半定规划法计算。采用核函数计算模糊相似度矩阵，有利于提高FJP算法对非线性数据特征的辨识能力，从而有利于减少传递闭包失真[16]。

4 数值实验

实验环境：CPU为Intel(R) Core(TM) i5-4200M，主频2.50 GHz，内存4 GB；操作系统Windows 8.1-64 bit，用Matlab (R2016a)实现算法。表1是测试数据集列表，前两个是UCI数据集，后三个是人工数据集。

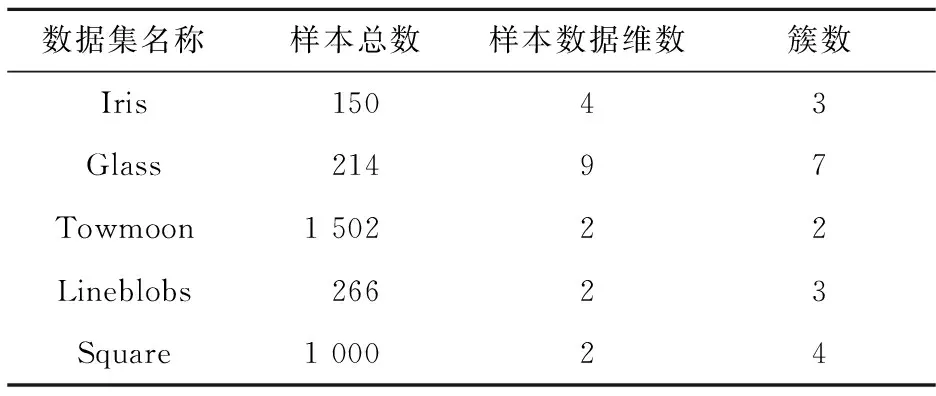
Table 1 Datasets in experiments表1 测试数据集列表

五个测试数据集所用的核函数参数如表2示，其中σ是高斯核函数的宽度，γ是高斯核与线性核的组合系数。参数σ和γ用文献[19]的方法确定。

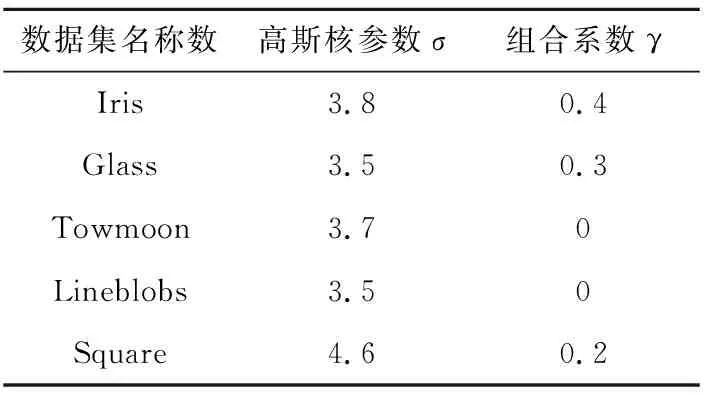
Table 2 Parameters chosen in kernel functions表2 核函数的参数列表

将本文IFJP算法与FJP-2008算法、FJP-2016算法作比较，其中FJP-2008算法采用固定的alpha值作为划分水平，FJP-2016算法采用动态的alpha值作为划分水平。用纯度(Purity)和标准化互信息NMI(Normalized Mutual Information)两个指标评价各算法的聚类效果[20]。纯度(Purity)指标的定义：令X的正确聚类簇为Ω={W1,W2,…,Wk}，纯度计算公式如下：

(6)

纯度值越高，表示算法的聚类准确率越高。NMI指标的计算方法如下：

(7)

(8)

(9)

NMI值在[0,1]，值越大表明算法的聚类效果越好。

表3是五个测试数据集上四种算法聚类结果的比较。根据表3，计算各算法在五个测试数据集上Purity指标的平均值，IFJP算法是82.3%，FJP-2008算法是55.6%，FJP-2016算法是57.2%。因此，在Purity指标平均值上，IFJP算法比FJP-2008算法高出26.7%，比FJP-2016算法高出25.1%；而FJP-2016算法仅比FJP-2008算法高出1.6%，两者的聚类准确度相差不大。Purity指标上的实验结果表明：传统FJP算法因传递闭包失真，包含了较多错误的关联信息，造成聚类准确度不高，FJP-2016算法虽然采用了动态alpha值划分水平但对改进聚类效果不明显，而本文采用基于核函数的桥元素填充法计算传递闭包，聚类准确度均明显优于FJP-2008算法和FJP-2016算法。所以，基于核函数的桥元素填充法生成传递闭包有效地降低了传递闭包的失真度。根据表3，计算各算法在五个测试数据集上NMI指标的平均值，IFJP算法是82.5%，FJP-2008算法是21.1%，FJP-2016算法是25.1%，由此可知，IFJP的聚类效果比FJP-2008算法和FJP-2016算法高出1倍以上，本文提出的算法使得聚类效果显著提升。同理，计算FCM算法Purity指标的平均值是79.9%，NMI指标的平均值是48.3%，两指标平均值均优于FJP-2008算法和FJP-2016算法的。这说明传统的FJP算法虽然引入传递闭包实现了自动模糊聚类，但因传统FJP算法的传递闭包计算方式存在缺陷，导致FJP聚类效果差于FCM，而本文采用基于核函数的桥元素传递闭包计算方法后，传递闭包中的关联信息更准确，聚类精度提高，故Purity、NMI指标均优于FCM的。综合上述实验结果分析，本文采用基于核函数的桥元素填充法计算传递闭包，有效地提高了FJP算法的聚类准确度，本文改进FJP算法聚类效果的思路是有效的、可行的。

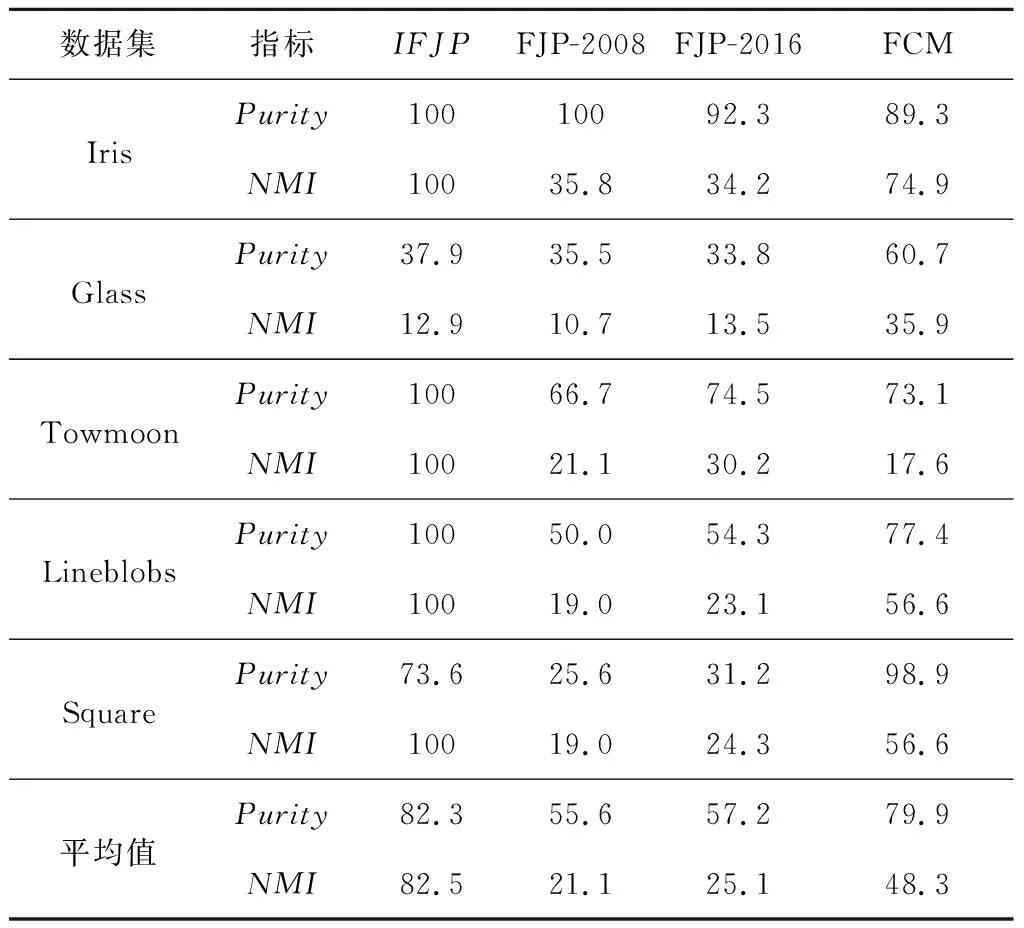
Table 3 Comparison of clustering results among the four algorithms表3 四种算法聚类结果的比较

在表1的五个测试数据集中，Lineblobs是一个二维的数据集，并且其平面图形的轮廓较其它测试集规整，容易从其聚类图中观察聚类效果的好坏，故本文选择Lineblobs数据集制作聚类效果平面图，如图1示。从图1可看出，三种FJP算法引入传递闭包后，利用传递闭包中的数据关联信息较好识别出扭转型曲线，但FJP-2008算法和FJP-2016算法因存在传递闭包失真问题，造成此数据集的三个簇仅识别出两个，而本文改进传递闭包计算方式后，有效降低了传递闭包失真，提高了传递闭包中数据关联信息的准确度，本文算法准确地识别出数据集的三个簇，取得了较好的自动聚类效果。因此，本文用桥元素填充法改进FJP算法聚类效果是有效的。

表4是四种算法在五个测试数据集上计算时间的比较，时间单位为秒(s)。在小型数据集上，例如Iris和Glass，三种FJP聚类算法的计算时间相当，但在其它三个大数据集上，本文的IFJP算法计算效率均优于FJP-2008算法和FJP-2016算法的。传统的FJP算法计算传递闭包时，需要反复扫描模糊相似度矩阵，所以生成传递闭包的计算时间较长，而本文采用桥元素填充操作取代原FJP算法的反复矩阵扫描操作，简单而高效，提高了FJP算法的计算效率，实验结果说明本文改进FJP算法的思路是有效的。

Table 4 Comparison of computing time of the three algorithms表4 三种算法计算时间的比较

对五个测试数据集进行复制，分别产生2倍(2×)、4倍(4×)、8倍(8×)、16倍(16×)的大型数据集，IFJP、FJP-2008、FJP-2016三种FJP算法在这些大型数据集上的计算时间随数据集规模变化的趋势如图1示。由图1可知：三种FJP算法的计算复杂度均具有多项式时间特性，前面的理论分析中曾指出：传统FJP算法的计算复杂度是O(n3)，本文所提IFJP算法的计算复杂度是O(n2)，均为多项式的时间复杂度，理论分析与实验结果符合。当数据集呈指数级(2n)增长时，本文算法的时间增加幅度明显小于传统FJP算法的，并且数据集规模越大，本文算法的计算效率优势越明显。图2的实验结果再次验证了本文桥元素填充法生成传递闭包的计算时间复杂度优于传统FJP算法的循环遍历相似度矩阵的最大-最小模糊关系合成闭包法。

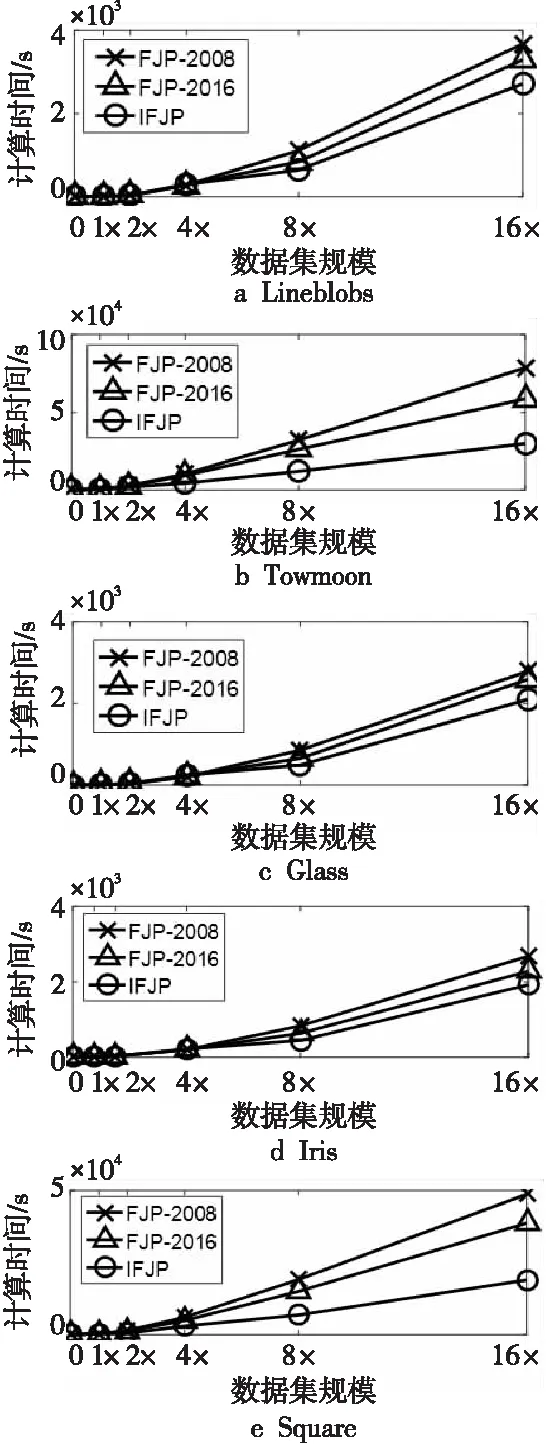
Figure 1 Running time vs.data set cardinality of three FJP algorithms图1 三种FJP算法计算时间随数据集规模变化的趋势

综合上述实验结果分析可知：本文采用桥元素填充法计算FJP算法的传递闭包，有效地提高了FJP算法的计算效率和聚类精度，本文改进FJP算法的思路是有效的、可行的。

图2是在五个测试数据集上，α划分水平与簇数目之间的关系，它反映了FJP算法的聚类特性。从图2可看出，当划分水平从1逐次减少时，簇的数目也逐渐减少并趋向稳定，从中可找出正确的簇数目。

以Lineblobs数据集为例，当划分水平α=1时，簇数目与样本个数相当；减少α水平，聚类产生的簇数目也随之减少。当α划分水平小于0.808 3时，簇数目维持1不变，剔除簇数为1的结果，出现划分次数最多的簇数为3，再取所有划分结果为3个簇的α划分水平中最小值作为αmin，以αmin对应的聚类结果此作为IFJP算法的最终聚类结果。

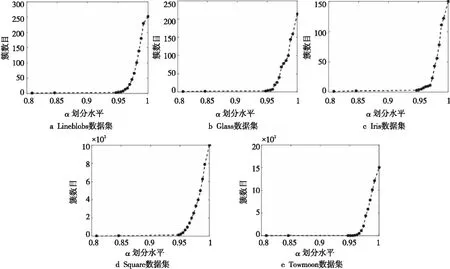
Figure 2 Relationship between α and the cluster number on datasets图2 各数据集上α划分水平与簇数目的关系

5 结束语

传统FJP算法生成的传递闭包存在失真问题，导致传递闭包中包含较多错误的关联信息，造成算法计算时间复杂度较高且聚类效果不理想。本文提出基于核函数的桥元素填充法计算传递闭包，能有效地提高传递闭包的计算效率，并且降低传递闭包的失真，提高聚类效果。在UCI数据集和人工数据集的实验结果表明，本文算法的计算效率和聚类效果均优于传统FJP算法的，本文改进FJP算法的思路是有效的、可行的。

[1] Zadeh L.Fuzzy sets[J].Information and Control,1965,8(3):338-353.

[2] Bezdek J C.Numberical taxonomy with fuzzy sets[J].Journal of Mathematical Biology,1974,1(1):57-71.

[3] Zhao Jin-shuai, Qiu Xiao-yan,Ma Jing-man,et al.Multi-objective optimization method of microgrid based on fuzzy clustering analysis and model recognition[J].Power System Technology,2016,40(8):2316-2323.(in Chinese)

[4] Xu Heng-peng,Li Yue,Shi Guo-liang,et al.The fitting component selection model of PM2.5 based on fuzzy clustering[J].China Environmental Science,2016,36(1):12-17.(in Chinese)

[5] Li Yang,Pang Yong-jie,Sheng Ming-wei.Side-scan sonar image segmentation via fuzzy clustering with spatial constrains[J].Journal of Image and Graphics,2015,20(7):865-870.(in Chinese)

[6] Haldar N A H，Khan F A，Ali A,et al.Arrhythmia classification using Mahalanobis distance based improved Fuzzy C-means clustering for mobile health monitoring systems[J].Neurocomputing,2017,220:221-235.

[7] Modava M,Akbarizadeh G.Coastline extraction from SAR images using spatial fuzzy clustering and the active contour method[J].International Journal of Remote Sensing,2017,38(2):355-370.

[8] Wang Ya-fei,Zhao Fei-fei,Chen Pei-pei.A framework of spatiotemporal fuzzy clustering for land-cover change detection using SAR time series[J].International Journal of Remote Sensing,2017,38(2):450-466.

[9] Thong P H, Son L H. A novel automatic picture fuzzy clustering method based on particle swarm optimization and picture composite cardinality[J].Knowledge-Based Systems,2016,109:48-60.

[10] Liu Han-bing,Wang Xian-qiang,Jiao Yu-bo.Damage identification for irregular-shaped bridge based on fuzzy C-means clustering improved by particle swarm optimization algorithm[J].Journal of Vibroengineering,2016,18(4):2149-2166.

[11] Nasibov E N,Ulutagay G.A new approach to clustering problem using the fuzzy joint points method[J].Automatic Control and Computer Sciences,2005,39(6):8-17.

[12] Nasibov E N,Ulutagay G.On the fuzzy joint points method for fuzzy clustering problem[J].Automatic Control and Computer Sciences,2006,40(5):33-44.

[13] Nasibov E N,Ulutagay G.A new unsupervised approach for fuzzy clustering [J].Fuzzy Sets and Systems,2007,158(19):2118-2133.

[14] Nasibov E N.A robust algorithm for solution of the fuzzy clustering problem on the basis of the fuzzy joint points method [J].Cybernetics and Systems Analysis,2008,44(1):7-17.

[15] Nasibov E N,Atilgan C.A note on fuzzy joint points clustering methods for large datasets[J].IEEE Transactions on Fuzzy Systems,2016,24(6):1648-1653.

[16] Zhu Jian-ying.Some common key problems and their dealing methods in the application of fuzzy mathematical methods[J].Fuzzy Systems and Mathematics,1992,6(2):57-63.(in Chinese)

[17] Lee H S.An optimal algorithm for computing the max-min transitive closure of a fuzzy similarity matrix[J].Fuzzy Sets and Systems,2001,123(1):129-136.

[18] Che Xiang-jiu, Liang Sen. Improved algorithm of SPIHT based on max-heap tree[J].Journal of Jilin University(Engineering and Technology Edition),2016,46(3):865-869.(in Chinese)

[19] Zhang Min, Qin Hua, Su Yi-dan. Reseach of semi-definite programming SVM model[J].Computer Engineering and Design,2011,32(5):1785-1788.(in Chinese)

[20] Christopher D M,Prabhakar R,Hinrich S.Introduction to information retrieval[J].Journal of the American Society for Information Science & Technology,2008,2(2):96-1.

附中文参考文献：

[3] 赵劲帅，邱晓燕，马菁曼,等.基于模糊聚类分析与模型识别的微电网多目标优化方法[J].电网技术,2016,40(8):2316-2323.

[4] 徐恒鹏,李岳,史国良,等.基于模糊聚类的PM2.5拟合组分选择模型的研究[J].中国环境科学,2016,36(1):12-17.

[5] 李阳，庞永杰，盛明伟.结合空间信息的模糊聚类侧扫声纳图像分割[J].中国图形图像学报,2015,20(7):865-870.

[16] 朱剑英.应用模糊数学方法的若干关键问题及处理方法[J].模糊系统与数学,1992,6(2):57-63.

[18] 车翔玖，梁森.一种基于大顶堆的SPIHT改进算法[J].吉林大学学报(工学版),2016,46(3):865-869.

[19] 张敏,覃华,苏一丹.半定规划支持向量机模型的研究[J].计算机工程与设计,2011,32(5):1785-1788.