基于不可满足原因的最小纠正集求解*

胡潇洒，张越岭，李建文，蒲戈光，张 敏

(华东师范大学计算机科学与软件工程学院，上海 200062)

1 引言

最小纠正集MCS(Minimal Correction Subset)是约束的集合。对于一个约束求解问题，MCS是其约束的子集。在布尔可满足性判定问题中，MCS是原公式的子集。与计算不可满足公式的最大不可满足的核MUC(Maximal UNSAT Core)类似，计算不可满足公式的MCS也是 NP-难问题[1]。MCS和MUC互为击中集(Hitting Set)问题[2]，因此可以通过计算MCS找到不可满足公式的MUC[3,4]。MCS还可以用于求解MaxSAT问题，通过多次计算MCS得到最大可满足子集SS(Maximal Satisfiable Subset)的集合，进而找到MaxSAT。对于可满足的公式，MCS也能够帮助其计算最大(小)的可满足解[5]。

在实际问题中，MCS也有着相应的应用[6,7]。由于MCS具有识别不可满足约束的最小原因的功能，能够帮助自动分析软硬件设计中的故障，通过计算MCS能够得到可能的出错原因，进而根据实际情况对软硬件故障进行修复[8 - 12]。由于软硬件系统通常较为复杂，拥有很大的状态空间，模型检查工作通常转换为软硬件系统内的可达性分析。通过使用MCS 计算两个状态之间不可达的原因，能够引导可达性分析问题中下一个状态的选取，对软硬件系统进行剪枝，实现加速模型检查的效果。MCS也可以用于实际的配置优化问题中，当用户给出的要求过于严格时，无法计算出一个完全符合要求的配置方案，通过计算MCS能够给出一个次优的配置方案，以尽量满足用户所提出的配置要求。用户根据MCS给出的配置方案，可以调整配置要求，最终找到一个用户满意且可行的配置方案。

本文提出了不可满足子句中的冲突算法CUC(Conflict in Unsatisfiable Clauses)，一种基于不可满足原因计算MCS的方法。CUC首先根据初始赋值，将公式分为可满足的子公式集合S和不可满足的子公式集合U。然后通过提取U中所出现的文字L(U)，并对L(U)进行分组，迭代判断L(U)中是否有文字可以加入到S中。当发现可加入的文字后，将所有出现该文字的子句从U中删除，并加入到S中。直到U中没有任何可加入S中的文字，当前的U子句集合即为MCS。

在CUC中，通过对L(U)进行分组，加速了L(U)的处理过程。对于一组文字g⊆L(U)，若g不能加入到S中，SAT(boolean SATisfiability)求解器将返回其不能加入(不可满足)的原因。通过对不可满足原因的分析，能够得到关键文字信息，进而加速MCS求解过程。

与其他求解MCS的工作相比，本文采用组合判定的方法，在可满足性求解搜索之前预先规定了一组文字的赋值，降低了可满足性求解所需要的时间。实验表明，与目前性能优秀的基于文字的提取LBX(Literal-Based eXtractor)[1]工具相比,CUC平均多求解65个(5%)公式，且求解效率比LBX快2.5倍。在4种不同的初始化策略中，CUC比LBX最多多求解出9%(113个)公式。

本文第2节给出文中所用到的定义和符号；第3节介绍所提出的CUC算法和 4种不同的初始化策略，并简单介绍本文根据已有算法所实现的LBX工具；第4节介绍CUC 与LBX的实验比较结果，并分析CUC占优势的原因；第5节对全文进行总结，并指出可能存在的问题。

2 预备知识

定义1(布尔变量) 布尔变量集合X={x1,…,xr}，文字是布尔变量xj(j=1,…,r)或者是布尔变量的否定xj。xj称为正文字，xj称为负文字。

定义2(布尔子句) 布尔子句由一组文字的析取组成，对于一个布尔子句φ=x1∨x2∨x3，我们称x1,x2,x3出现在φ中，即x1,x2,x3∈φ。

定义3(布尔公式) 布尔公式由布尔子句合取组成，对于一个布尔公式F=φ1∧φ2∧φ3，我们称φ1,φ2,φ3出现在F中，即φ1,φ2,φ3∈F。

为了讲解方便，我们使用变量、子句、公式代替布尔变量、布尔子句、布尔公式。给定一个公式F，我们使用cls(F)表示公式中出现的所有子句集合，用var(F)表示公式中出现的所有变量集合，用lit(F)表示公式中出现的所有文字集合。对于一个给定子句φ，我们使用var(φ)表示子句中出现的所有变量集合，用lit(φ)表示子句中出现的所有文字集合。对于所有集合Z，我们用|Z|表示集合的长度，即集合中元素的个数。

定义4(赋值) 对于变量集合X={x1,…,xr}，赋值是一个映射μ:X→{0,1},当μ(xi)=1时，i=1,…,r,μ(xi)=0。当μ(xi)=1时，μ(xi)=0。

通过计算公式F中每个变量的赋值，根据布尔公式中∧和∨的计算规则，能够得出F的整体赋值。给定一个赋值μ，若F在μ的赋值情况下真值为1，则F可以被μ满足，μ是F的一个解。若F在μ的赋值情况下真值为0，则F不可以被μ满足。若F不存在一个解，则F不可满足。

定义5(MCS) 对于不可满足公式F，MCS⊆F,是F的一个子集，且FMCS可满足，对于MCS中任一子句φ，FMCS∪{φ}不可满足。本文所研究的问题即为不可满足公式的MCS求解问题。

一个不可满足公式F如下:

F=(x1∨x2∨x3)∧(x1∨x2)∧x1∧x3∧(x4∨x5∨x6)∧(x4∨x5)∧x4∧x6

其中,变量集合为X={x1,x2,x3,x4,x5,x6}，子句集合C={c1=(x2∨x2∨x3),c2=(x1∨x2),c3=x1,c4=x3,c5=(x4∨x5∨x6),c6=(x4∨x5),c7=x4,c8=x6}。则子句集合C={c3,c7}为公式F的MCS，从F中移除C后，剩余集合：FC=(x1∨x2∨x3)∧(x1∨x2)∧x3∧(x4∨x5∨x6)∧(x4∨x5)∧x6可满足，且(x1∨x2∨x3)∧(x1∨x2)∧x3∧(x4∨x5∨x6)∧(x4∨x5)∧x6∧x1和(x1∨x2∨x3)∧(x1∨x2)∧x3∧(x4∨x5∨x6)∧(x4∨x5)∧x6∧x4均不可满足。

3 基于不可满足原因的最小纠正集求解方法

本文所提出的算法思想如下：对不可满足公式进行分组，使用不可满足原因，迭代分析公式中当前不可满足的部分能否被其他赋值满足，进而找到最小不可满足的部分，即为当前公式的MCS。我们通过一个简单例子说明CUC的工作流程。

对于一个不可满足公式：

F=(x1∨x2)∧(x1∨x2)∧(x1∨x2)∧(x1∨x2)∧(x3∨x4)

首先使用初始化赋值μ(x1)=1,μ(x2)=1,μ(x3)=0,μ(x4)=0将F分为可以被μ满足的子集S和不可以被μ满足的子集U两个部分，其中

S={(x1∨x2),(x1∨x1),(x1∨x1)}

U={(x1∨x2),(x3∨x4)}

CUC计算U中的所有文字lit(U)，并对lit(U)进行分组。lit(U)={x1,x2,x3,x4}。CUC将lit(U)分为组，每组包含个文字。在当前例子中，lit(U)被分为两组，每组包含两个文字。第一组为{x1,x2}，第二组为{x3,x4}。

CUC通过SAT求解器判断是否存在一个新的解μ′，使得分组中每个文字在μ′中的赋值为1。对于第一组，CUC通过求解S∧x1∧x2判断是否存在一个新的解μ′，μ′满足S，且μ′(x1)=1,μ′(x2)=1。由于不存在这样一个新的μ′ ，SAT求解器返回不可满足的原因{x1,x2}。CUC将删除不可满足原因中的第一个文字，判断剩余的文字所组成的单元子句能否加入到S中。在这个例子中，S∧x1和S∧x2均不可满足，不存在一个新的解μ′，U中没有新的子句可以加入到S中。在完成第一组文字分组的判定之后，CUC继续处理剩余的文字分组，在当前的例子中，S∧x3∧x4可满足，存在一个新的{x3,x4}所组成的单元子句可以加入到S中，U中所有包含x3或x4的子句可以加入到S中，CUC将{x3∨x4}加入到S中。此时，U中所有的文字均已处理，MCS求解完成，求得的MCS为{(x1∨x2)}。

计算MCS(CUC算法)流程描述如下：

算法1计算MCS

输入:不可满足公式F;

输出:最小修正子集MCS。

1: (S,U) ←initialAssignment(F);

2: (L,B,Lc) ← (L(U),∅,∅)

3: whileL≠ ∅ do

4:Lc ←removeLiterals(L,m);

5: (sat,μ,conflcit) ←SAT(S∪B∪Lc);

6: ifsatthen

7: (S,U) ←updateSatClauses(μ,S,U);

8: else

9:dealConflict(S,conflict,Lc);

10: returnMCS=FU

算法1中，F是不可满足的公式，S和U是F的子集，S∪U=F；L是U中文字的集合;B是CUC在求解过程中找到的关键文字集合;Lc是L的子集，表示当前正在处理的文字分组。

算法1的详细过程如下:

第1行给定不可满足公式F，使用initialAssignment方法将F分为子公式集合S和U两部分。

第2行将所有出现在U中的文字放入L中，B和Lc初始化为空集。

第3行根据U中的文字集合L，开始循环计算U中可以加入到S中的子句。在循环过程中，不断从L中移除已经访问过的文字，直到L变为空集。循环的终止条件是U中所有的文字都已标记为已访问。

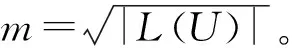
第5行求解公式S′:=S∪B∪Lc的可满足性，返回结果为三元组(sat,μ,conflict)。若S′可满足，sat为true，μ为S′的一个解，conflict为空集；否则sat为false，μ为空集，conflict为S′ 不可满足的原因。

第6、7行当sat为 true时，调用updateSatClauses方法将U中的子句加入到S中。

第8、9行当sat为 false，即S′不可满足时，根据得到的conflict使用dealConflict继续求解当前文字分组中能够加入到S中的单元子句，进而计算能够加入到S中的子句。

第10行最终的MCS为F和S的差集。

CUC设计并实现了4种不同的initialAssignment方法，分别为:

(1) 全0(-0)初始化策略:将所有的正文字赋值为0，负文字相应地赋值为1。

(2) 全1(-1)初始化策略:将所有的正文字赋值为1，负文字相应地赋值为0。

(3) 随机初始化(-random)策略:随机决定所有正文字的赋值，负文字相应地取反赋值。

(4) 最大出现次数(-max)初始化策略:计算其相应正负文字的出现次数，将出现次数较多的文字赋值为1。比如，在公式F中，若文字a的出现次数为10次，文字a的出现次数为5次，则a的赋值为1，a的赋值为0。

在removeLiterals方法中，CUC从L中顺序选取m个文字，并将其加入到Lc中形成当前正在处理的文字分组。由于CUC保证一个分组结束之后才会开始计算下一个分组，因此从L中直接移除这m个文字，并将其标记为已访问。

在updateClauses方法中，CUC根据得到的解μ将U中的子句加入到S中。对于所有U中的子句，若其所包含的文字中至少有一个文字在μ中的赋值为1，则当前子句可以加入到S中。即对于∀φ∈U,φ可以加入到S中，当且仅当∃a∈φ,μ(a)=1。当子句φ加入到S中后，CUC将φ从U中移除。

当算法1中第5行的可满足性求解结果为不可满足时，CUC根据当前分组及其所返回的原因继续计算MCS，其算法伪代码如算法2所示。

算法2CUC不可满足原因处理算法dealConflict(S,conflict,L)

输入:可满足子公式S，不可满足的原因conflict，文字分组Lc;

输出:文字分组Lc中的文字是否均完成处理。

1:(len,vlen)←(|L|,0);

2:if |conflict| == 1 then

3:B←B∪{conflict};

4:vlen++;

5:whilelen≠vlendo

6:a=conflict[0];

7: (sat,μ,conflict′)←SAT(S∪B∪a);

8: ifsatthen

9: (S,U) ←updateSatClauses(μ,S,U)

10: else

11:B←B∪(a)

12: (sat,μ,conflcit′)←SAT(S∪B∪(conflicta}))

13: ifsatthen

14: (S,U)←updateSatClauses(μ,S,U)

15: break

16: else

17:dealConflict(S,conflict′,conflicta}))

18:vlen=vlen+|conflict|;

19:return true

算法2中，len为当前文字分组Lc的长度，vlen为当前分组中已完成处理的文字个数。

算法2的详细过程如下:

第1行len初始化为当前输入的文字集合的长度，vlen初始化为0。

第2～4行当前输入的不可满足原因conflict长度为1时，将原因中唯一的文字的反加入到关键文字集合B中，将已完成处理的文字个数加1。

第5行当Lc中还存在未处理的文字，len≠vlen时，且len≠ 1，循环处理Lc中剩余的未处理文字，直到所有文字均已完成处理。

第6～11行取出当前不可满足原因集合中的第1个文字a，判断单元子句a能否加入到S中。若单元子句a可以加入到S中，则根据第9行中得到的解μ更新S；若单元子句a不能加入到S中，则执行第11行，将文字a的反加入到关键文字集合中。

第12行使用移除了第1个文字a后的不可满足原因conflict计算能够加入到S中的子句，若存在能够加入到S中的子句，则执行第14行更新S；若仍然不存在能够加入到S中的子句，则根据第12行返回的新的不可满足原因递归执行dealConflict方法，处理新的不可满足原因，继续计算能够加入到S中的子句。

4 实验结果

实验结果显示，CUC整体性能比LBX好。综合4种策略，CUC平均计算出1 249个公式，LBX平均计算出1 184个公式，CUC比LBX平均多计算出5%的公式。在LBX与CUC均能够解出的公式中，LBX的平均计算时间为0.44 s，CUC的平均计算时间为0.18 s，比LBX快了2.5倍。

4.1 实验环境与数据集设置

本文使用Minisat 2.2[5]作为可满足性求解器，使用C++语言设计并开发了CUC工具，用于计算不可满足的布尔公式的最小纠正子集。工具的下载链接为http:∥lab301.cn/blog/?page_ id=168&lang=en。

实验的运行服务器为Intel i7处理器，运行内存限制为4 GB，ijcai13-bench中的公式运行时间限制为30 s，maxsat14-bench中的公式运行时间限制为180 s。由于maxsat14-bench中的公式求解更加困难，我们在实验中为其设置了比ijcai13-bench中公式更长的运行时间限制。

通过查阅参考文献[1,14]中的实验部分发现,LBX[1]是目前求解效率最高的MCS求解工具。我们选用LBX作为比较的工具，但由于LBX不提供开源代码，因此本文按照LBX文中的描述，重新实现了LBX的工具。

LBX算法同样根据初始赋值将不可满足公式F分为可满足子集S和不可被满足子集U两个部分。LBX通过逐个判断U中文字能否加入到S中的方法，找出U中所有可以加入到S中的子句，进而求出F的MCS。

我们严格按照参考文献[1]中算法1对LBX求解算法的描述实现了LBX。由于参考文献[1]中没有详细说明LBX中的初始化策略，我们使用与CUC中相同的4种初始化策略，实现了 LBX的4种不同的初始化策略，即LBX-1、LBX-0、LBX-random和LBX-max。

本文选用的测试数据集包括：ijcai13-bench[1],共1 642个，其所包含的公式均为合取公式;maxsat14-bench,共105个[1]，选取了2014年MaxSAT比赛中公式规模小于30M的公式。

4.2 初始化策略分析

图1给出了CUC与LBX在4种不同初始化策略下能够求解出的公式个数情况。通过比较发现，除了LBX-random 初始策略外，CUC的求解个数均多于LBX的求解个数。而由于LBX-random初始策略具有随机性，因此其数据对性能的反应具有偏差。

Figure 1 Number of instances whose MCS can be solved by the two algorithms under four strategies图1 两种算法在4种不同策略下可以求解出MCS的实例数量

表1给出了在ijcai13-bench 数据集中，LBX与CUC能够同时求解出的公式个数，及相应的求解时间和平均求解时间。结果表明CUC在不同策略下的性能均要优于LBX，平均求解效率是LBX的2.5倍。在4种不同的初始化策略下，求解同样的公式，CUC所需的总时间均小于LBX所需总时间。值得注意的是，虽然CUC-random的求解时间与LBX-random 的求解时间相差最大，但由于LBX-random能够求解出的公式数量较少，且多数为简单公式，因此该组时间差距最大。

Table 1 Analysis of the formulas which can be solved by both CUC and LBX表1 CUC与LBX均可求解的公式分析结果

图2展示了LBX和CUC在不同策略和不同时间内求解出的公式个数的变化。在1 642个公式中，存在部分公式使用LBX和CUC计算MCS的平均求解时间小于0.01 s。为了使图表更加清晰，图2中仅选择了LBX和CUC的平均时间大于0.01 s的公式进行分析。CUC-max、CUC-1、CUC-0可求解公式的个数均大于LBX的相应策略。

上述实验结果表明，CUC在CUC-1、CUC-0初始化策略下，求解公式个数均多于 LBX的，总求解时间和平均求解时间均小于LBX的求解时间。依据图2展示的LBX和CUC在-max策略下不同时间求解出的公式个数的变化，在相同时间下，CUC求解出的公式个数均大于LBX的，换言之求解出相同个数公式的情况下，CUC效率高于LBX，如表3所示，其平均求解时间比LBX快2.5倍。最为重要的是，CUC可以求解出LBX无法在规定时间内求解出的公式，这表明 CUC的平均性能优于LBX。分析CUC求解数据情况可知，CUC-0与CUC-max的性能优于其他两种策略。CUC-max能够比CUC-0多求解出46个公式。在520 s时，CUC-max求解个数比 CUC-0多了9个，时间超过520 s，CUC-max可以求解出在规定时间内CUC-0无法求出的公式，占总公式2%。由此可知，CUC-max性能优于CUC-0，在4种不同的初始化策略中最优。而分析LBX求解数据情况也可以发现，LBX-max能够求解出的公式个数在LBX的4种策略中最多，其求解公式数量仅次于CUC-max的。因此，在4种初始化策略中，-max初始化策略的性能最优。这是因为-max初始化策略通过不停地选择未赋值文字出现次数最多的文字，能够使得初始化赋值尽量满足更多的子句。在后续的计算过程中，仅有较少的未满足子句需要使用CUC或LBX方法进行判定，节省了判定过程中调用可满足性求解器的次数，加快了LBX和CUC的求解效率，缩短了求解时间。

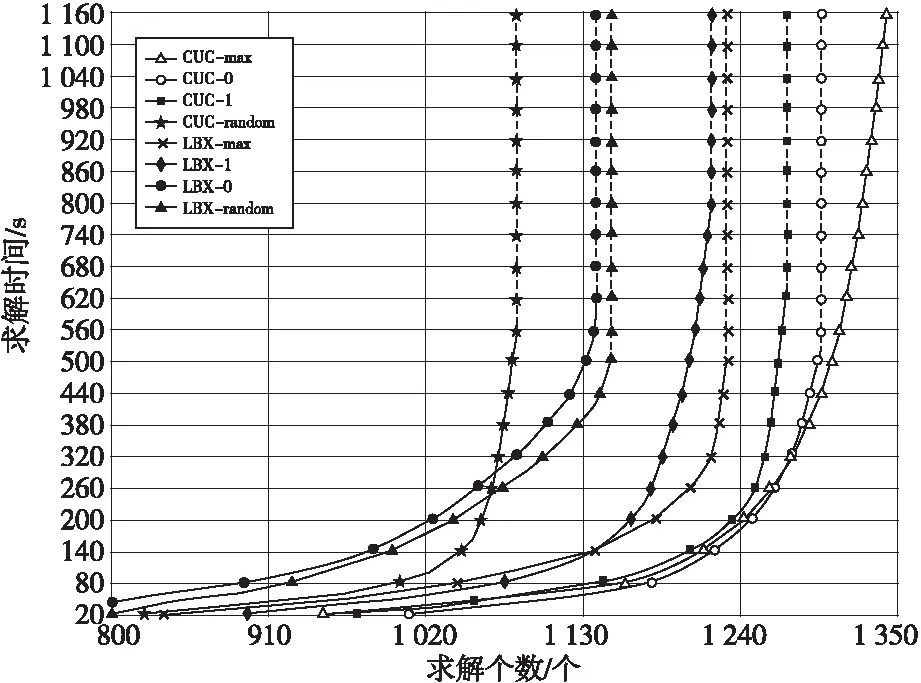
Figure 2 Running times for ijcai13-bench instances图2 ijcai13-bench运行时间图

图3展示了CUC-max与LBX-max在不同时间内求解出的公式个数的变化。CUC-max的求解个数优于LBX-max的。由于选取的公式在规定的时间内求解出MCS较为困难，CUC与LBX均只能求解出较少的公式，CUC-max能够求解出10个公式， LBX-max能够求解出5个公式，所有LBX-max能够求解出的公式，均可以由CUC-max求解得出。

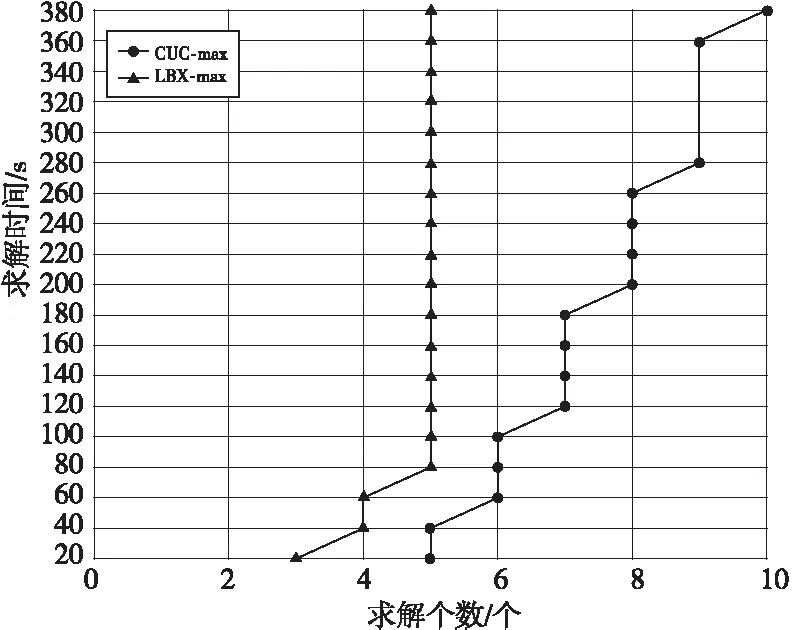
Figure 3 Running times for MaxSAT instances图3 MaxSAT运行时间图

5 相关工作

MCS计算问题作为一种研究不可满足约束的主要方法，从1987年开始就引起了研究学者的关注，并应用于基于可满足性分析的模型故障分析之中[12]。MCS求解方法主要分为迭代求解公式可满足性的方法和根据初始化赋值构建最大可满足公式的方法两类。

迭代求解公式可满足性方法主要包括线性搜索方法[15]、松弛文字方法[16]和FASTDIAG方法[17]。

Bailey等人[15]使用线性搜索方法求解公式F的MCS集合C。线性搜索算法从MCS的定义出发，每次选择一个子句c∈F，并将c从F中移除，判定Fc的可满足性，若Fc可满足，则完成了对C的计算，若Fc不可满足，则继续选择另一个子句c′，并判定Fc∪c′的可满足性。线性搜索算法通过不断地从原公式F中删除子句的方法，能够找到一个子句集合M，使得FM可满足，且对于M中的任一子句m，FM∪m均不可满足。M就是原公式F的MCS集合。对于同等的布尔约束公式，当公式不可满足时其可满足性评价判定时间较长，线性搜索算法中的大部分需要判定可满足性的公式均为不可满足公式，因此线性搜索的平均搜索时间较长。

Liffiton等人[16]提出了使用最大可满足子集计算MCS的方法。为了避免多次判定不可满足公式的可满足性，节省判定时间，最大可满足子集方法为原公式中每个子句增加了一个松弛文字l，所生成的新公式为F′，c′一定存在一个解μ，μ中所有的松弛文字均被赋值为1，则F′一定是可满足的。最大可满足子集方法不断搜索新的解，并希望在新的解中赋值为1的松弛文字个数不断减少。当不存在能够将赋值从1改为0的松弛文字时，最大可满足子集方法结束搜索，最终的MCS是那些松弛文字赋值为1的子句组成的集合。

Felfernig等人[17]提出了FASTDIAG算法，使用分而治之的思想计算MCS。FASTDIAG算法递归地分析原公式F不可满足的原因。FASTDIAG算法将F逐层分解为子公式，每层两个子公式均由上层的子公式一分为二而来。通过将不可满足的原因分解到两个子公式中，逐层分析出原公式的最小不可满足原因MCS。

在通过初始化赋值构建最大可满足公式的MCS求解方法中，为了避免判定公式不可满足所需的大量时间，MCS提取算法在调用求解器之前，先生成初始化赋值μ，根据μ将原公式F分为能够被μ满足的子集S和不能被μ满足的子集U，该类方法主要有D子句算法CLD(Clause D)[18]、分区算法CMP(Computational Method for Partitioning)[4]和LBX方法[1]。

Marques-Silva等人[18]提出了CLD算法。CLD算法根据初始化赋值，将原公式分为子公式集合S和U两个部分，子公式集合S能够被初始化赋值满足，子公式集合U不能够被初始化赋值满足。CLD算法统计所有出现在子公式集合U中的文字Lit(U)，并将这些文字析取连接，生成一个新的子句clauseD，即clauseD=∨l,l∈Lit(U)。将子句ClauseD合取加入到子公式集合S中，判定S∧clauseD的可满足性。若S∧clauseD可满足，则根据所得到的解更新S和U；若不可满足，则说明当前的U即为MCS。

Grégoire等人[4]提出的CMP算法也使用初始化赋值将原公式划分为可满足子公式集合S及其补集U。CMP算法利用MCS和MUC计算互为击中集问题的性质，通过计算变迁子句(Transition Clause)来计算MCS。假设一个不可满足的公式F存在多个不可满足的最小核(MUC)，即F中存在多组由于互相冲突导致无法同时可满足的子句集合。为了消除冲突，找到可满足子公式，需要解决每个MUC的冲突。根据MUC的性质，从MUC 子句集合中任意移除一条子句即可解决该MUC的冲突。因此，从每个MUC中移除一条子句即可使得到的子公式可满足，所移除的所有子句组成了MCS。CMP提出了一种从MUC中找到一条子句的方法，进而能够计算MCS。需要注意的是，计算MUC的时间开销较大，因此CMP没有选择通过计算得到所有的MUC。CMP首先从U中选择一条子句c，计算S∧Uc的可满足性，若公式可满足，则根据所得到的解更新子公式集合S和U，并将c放入MCS集合中，c是CMP找到的一个能够解决相应MUC冲突的变迁子句。若公式不可满足，则将c从U中移除，之后重新选择一条子句c′，重复上述步骤。已经放入 MCS中的子句c不会再次出现在子公式集合S和U中，当存在一个赋值，其计算出的子公式集合U为空集时，CMP算法结束，返回计算得到的MCS。

Mencia等人[1]提出的LBX算法首先根据初始化赋值将原公式划分为可满足子公式集合S及其补集U。之后，LBX算法调用CLD算法计算所有出现在子公式集合U中的文字，与CLD算法不同的是，LBX算法将U中出现的文字构建为单元子句，逐个地加入到S中。LBX算法每次选取一个构建的单元子句c，判定是否可满足，若可满足，则根据求得的解更新S和U，若不可满足，继续选择下一个单元子句c进行判定。已判定过的单元子句不会重复判定，当所有的单元子句均判定结束后，LBX算法结束，最终得到的U即为 MCS。与CUC算法相比，CLD算法将出现在子公式集合U中的文字组成一个新的子句，容易导致新生成的子句过长，影响可满足性求解器的求解效率。在CMP的运行过程中，对不可满足公式的判定次数明显多于对可满足公式的判定次数，算法整体的可满足性判定效率因此降低。LBX算法对每个出现在子公式集合U中的文字均调用一次可满足性求解判定其是否出现在MCS 中，对可满足性求解的利用效率较低。

6 结束语

本文提出了一种基于不可满足计算MCS的CUC算法和工具。CUC通过分析不可满足的原因，改进LBX求解MCS的算法，减少了调用SAT求解器的次数，最终加速了求解过程。与LBX比较，CUC能够通过一次可满足性求解确定多个文字是否出现在最终的MCS中，而LBX中的一次可满足性求解只能确定一个文字是否出现在最终的MCS中。通过与已有LBX的实验比较发现，CUC能够使用更少的求解时间求解出更多的公式。总体而言，与LBX工具相比，CUC在求解MCS时更具有优势，特别在初始赋值使用-max策略时，CUC的优势更为显著，对于CUC和LBX同时可以解出的公式，CUC平均求解时间比LBX快2.5倍。

[1] Mencia C,Previti A,Marques-Silva J.Literal-based MCS extraction[C]∥Proc of the 24th International Joint Conference on Artificial Intelligence, 2015:1973-1979.

[2] Reiter R.A theory of diagnosis from first principles[J].Artificial Intelligence,1987,32(1):57-95.

[3] Liffiton M H,Previti A,Malik A,et al.Fast,flexible MUS enumeration[J].Constraints,2016,21(2):223-250.

[4] Grégoire E,Lagniez J M,Mazure B.An experimentally efficient method for (MSS,CoMSS) partitioning[C]∥Proc of AAAI,2014:2666-2673.

[5] Kavvadias D J, Sideri M,Stavropoulos E C.Generating all maximal models of a Boolean expression[J].Information Processing Letters,2000,74(3-4):157-162.

[6] Xu Dao-yun. Applications of minimal unsatisfiable formulas to polynomially reduction for formulas[J].Journal of Software,2006,17(5):1204-1212.(in Chinese)

[7] Yin Ming-hao, Lin Hai,Sun Ji-gui. Solving #SAT using extension rules[J].Journal of Software,2009,20(7):1714-1725.(in Chinese)

[8] Koitz R,Wotawa F.SAT-based abductive diagnosis[C]∥Proc of the 26th Internatinal Workshop on Principles of Diagnosis,2015:167-176.

[9] Walter R, Felfernig A, Küchlin W.Constraint-based and SAT-based diagnosis of automotive configuration problems[J].Journal of Intelligent Information Systems,2017,49(1):87-118.

[10] Arif M F, Mencía C,Ignatiev A,et al.BEACON:An efficient SAT-based tool for debugging εL ontologies[C]∥Proc of International Conference on Theory and Applications of Satisfiability Testing,2016:521-530.

[11] Arif M F, Mencía C,Marques-Silva J.Efficient axiom pinpointing with EL2MCS[C]∥Proc of Joint German/Austrian Conference on Artificial Intelligence (Künstliche Intelligenz),2015:225-233.

[12] Bekkouche M,Collavizza H,Rueher M.LocFaults:A new flow-driven and constraint-based error localization approach[C]∥Proc of the 30th Annual ACM Symposium on Applied Computing,2015:1773-1780.

[13] Eén N,Sörensson N.An extensible SAT-solver[C]∥Proc of International Conference on Theory and Applications of Satisfiability Testing,2003:502-518.

[14] Mencía C,Ignatiev A,Previti A,et al.MCS extraction with sublinear oracle queries[C]∥Proc of International Conference on Theory and Applications of Satisfiability Testing,2016:342-360.

[15] Bailey J,Stuckey P.Discovery of minimal unsatisfiable subsets of constraints using hitting set dualization[C]∥Proc of the 7th International Symposium on Practical Aspects of Declarative Languages,2005:174-186.

[16] Liffiton M H,Sakallah K A.Algorithms for computing minimal unsatisfiable subsets of constraints[J].Journal of Automated Reasoning,2008,40(1):1-33.

[17] Felfernig A,Schubert M,Zehentner C.An efficient diagnosis algorithm for inconsistent constraint sets[J].AI EDAM,2012,26(1):53-62.

[18] Marques-Silva J,Heras F,Janota M,et al.On computing minimal correction subsets[C]∥Proc of the 23rd International Joint Conference on Artificial Intelligence, 2013:615-622.

附中文参考文献：

[6] 许道云.极小不可满足公式在多项式归约中的应用[J].软件学报,2006,17(5):1204-1212.

[7] 殷明浩,林海,孙吉贵.一种基于扩展规则的#SAT求解系统[J].软件学报,2009,20(7):1714-1725.