高斯光束通过颗粒系统的衰减特征

王 涵, 周哲玮,张金松, 张建华,王志亮

(1.上海大学上海市应用数学和力学研究所,上海200072;2.上海大学机电工程与自动化学院,上海200444)

有机发光二级管(organic light-emitting diode,OLED)是近年来迅速发展起来的一种新型显示器件.相对于传统显示技术,OLED具备轻薄、可弯、自发光、色彩还原度高、低压效、可视角度大等优点,并且在照明、电子产品显示及工业仪器仪表等领域都呈现出较好的应用效果,从而成为近些年显示技术领域的研究热点.

早期一些学者们所研究生产的有机电致发光器件,由于其驱动电压太大或成品质量差、效率低等问题而一直未被重视[1-3].直到1987年,美国Kodak公司率先发现了低分子有机材料的发光特性,并制备出低电压、高效率的OLED器件,人们才开始对这种新型显示技术产生了研究兴趣,OLED显示技术也在近30年来得到了飞速发展[4-5].如今,市面上已经有了各种各样的OLED产品(主要集中在小屏幅产品),但其价格与其他同类产品相比要高出许多,主要原因是高额的制造成本:①高纯的有机发光材料的价格十分昂贵;②在制备OLED器件过程中材料的利用率很低.OLED的制备方法[6-8]以真空蒸镀工艺为主,在蒸镀过程中被蒸发的有机分子很容易脱离而向靶外溅射,只有少数有机分子运动到基板形成薄膜(＜15%),使得材料的利用率低,镀膜的沉积时间长.近年来,针对提高有机材料利用率这一问题,研究人员提出了一些新的方法[9-10].与前人工作不同,本课题组提出了利用光束来导向真空蒸镀过程中有机发光分子射流的运动,从而提高有机分子材料的利用率.

利用光束操纵微粒的技术原理是基于光的辐射压力作用.1873年,Svoboda等[11]发表的电磁场理论表明,光可以产生辐射压力.随着激光的问世,1986年,Ashkin等[12]利用高聚焦的激光束成功地对颗粒实现2维束缚,随着各种新型激光的发明以及光力学效应的不断发展[13-15],许多不同材料及形状的颗粒都可以被运用光学来实现精确操控或限制活动范围[16-17].因此,针对真空蒸镀工艺中存在的材料利用率低这一问题,本课题组以光学理论为桥梁,研究光束对粒子流的操控以及二者之间的相互影响关系,解决真空蒸镀中材料利用率低的问题.通过研究多粒子体系对光的能量衰减,重点讨论粒子光学、颗粒及其作用表征量与坡印廷矢量衰减规律之间的关系,以期获得颗粒射流在光约束下的力学行为.

1 理论基础与方法

1.1 广义Mie理论

1908年,德国科学家Mie在给出了平面波源的条件下,单个均匀球体粒子在散射场下的精确解,即Mie理论[18].1988年Gouesbet等[19]以Mie理论为基础,利用Bromwich公式进一步提出了广义Lorenz-Mie理论,并给出了在Gauss光束入射情况下均匀球体粒子的消光截面、散射截面等表达式.而后,Xu[20]发展了广义Mie理论,成功解决了由多粒子所构成的群聚体的光散射问题.因此,本工作以广义Lorenz-Mie理论为基础,研究光与粒子间的各类相互作用.

众所周知,麦克斯韦方程在时谐电磁场问题中可以简化为亥姆霍兹方程,即

式中,k=2π/λ为波数,λ为波长;E和H分别为空间时谐电磁场分布,由于E场与H场展开方式类似,故只以时谐电场E为例进行简单说明.

在以任意球体粒子i的中心为原点的球坐标系下,将第i个粒子的入射场、散射场和激励场分别以矢量球谐函数展开[21-22]:

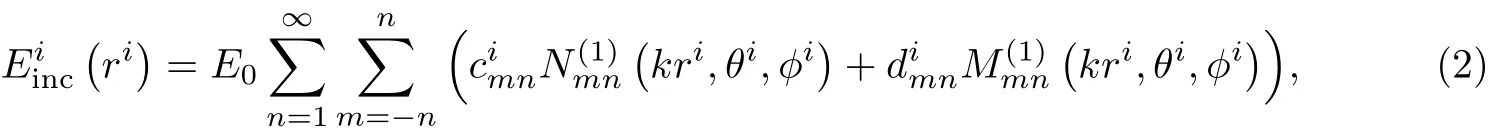
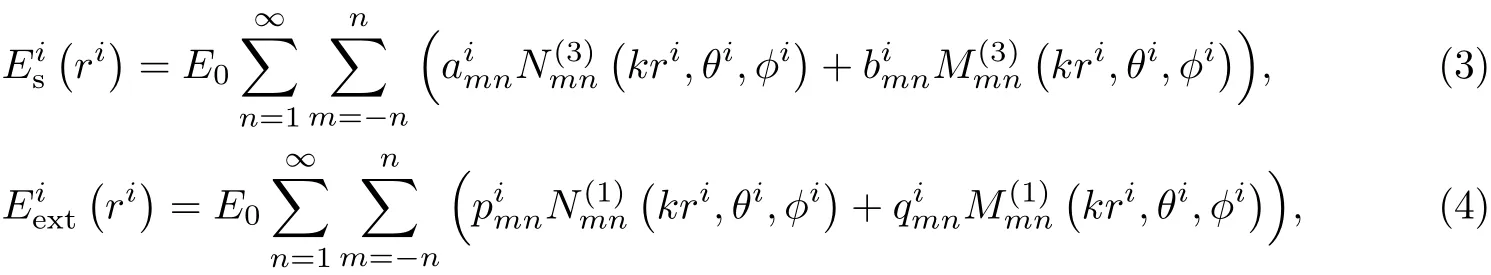
式中,与dimn为入射场展开系数,由入射波束中心场强振幅和波形系数决定[23-24];aimn与为单粒子的散射场展开系数;与为单粒子的激励场展开系数;ri,θi,ϕi分别代表第i个粒子在球坐标中的位置;与为满足亥姆霍兹方程的矢量球谐函数,具体形式如下:

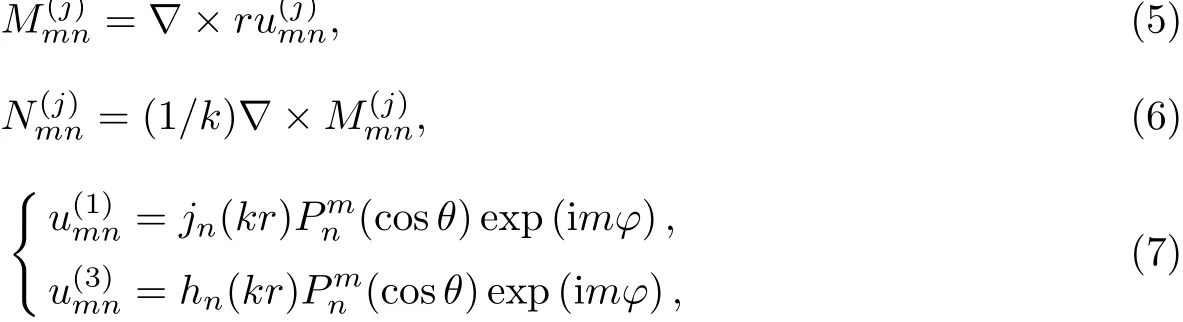
式中,是标量球谐函数,jn与hn=jn+iyn为球Bessel函数和球Hankel函数,为缔合Legendre函数,r为无量纲化的径向位置.

在多粒子体系中,某个粒子的散射场对其他粒子存在一定的影响,故i粒子表面的激励场应当由外部入射场以及体系中其他粒子的散射场的和组成,即

式中,Ns为散射量粒子数,由于要进行散射场的叠加,故将以j为展开中心的球谐函数转换为以i为展开中心的球谐函数,这一步由加法定理实现[11]:

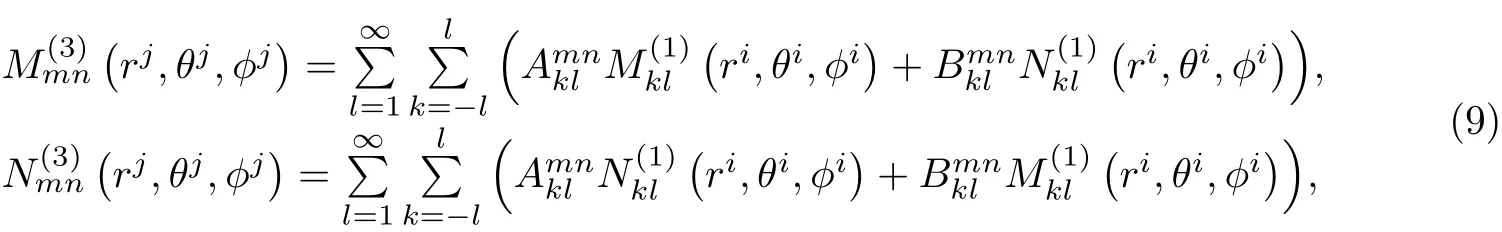
式中为加法系数,由任意2个粒子之间的距离和位置确定.接下来再利用粒子表面边界条件以及三角函数、缔合Legendre函数的正交性,可得到将散射场系数由入射场系数、粒子尺寸参数和复折射率表示的线性方程组:

式中为入射场系数,Tji为多粒子体系中j和i粒子之间的传输矩阵:为散射场系数,

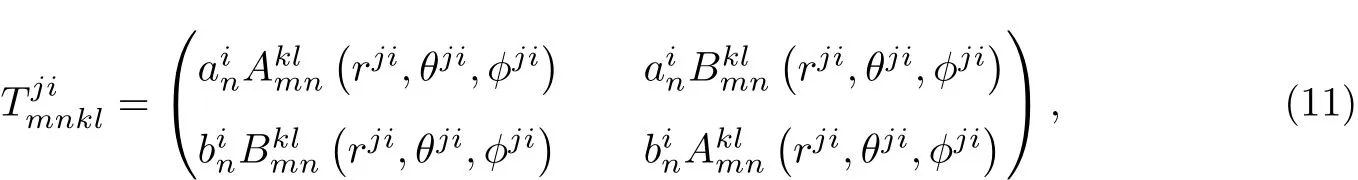
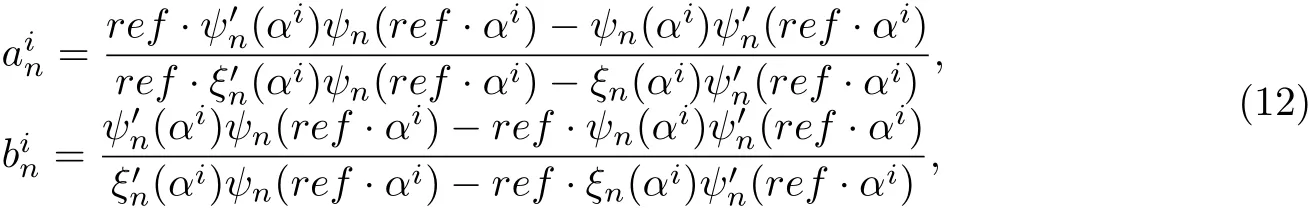
式中,为Mie散射系数,仅依赖于球粒子的尺寸参数ai=2πri/λ和相对折射率ref;ψn和ξn为Ricatti-Bessel函数.这样便可得到入射场系数与散射场系数之间的关系,进一步利用式(4)来得到整个多粒子体系中场的分布.

1.2 坡印廷矢量

坡印廷矢量反应了光束能流密度,表示单位时间内电磁场的能量通量.在多粒子体系中,坡印廷矢量S的表达式为

其中,

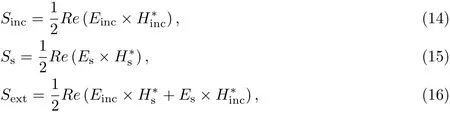
式中,∗表示取共轭,Sinc由入射场决定,Ss由散射场决定,Sext由入射场与散射场相互作用决定.利用上述算法可求得多粒子体系内的电磁场分布,然后代入坡印廷矢量中即可求得整个体系中的坡印亭矢量;再通过改变体系中粒子的光学特征,观察坡印廷矢量的变化情况,进一步找到多粒子体系中粒子的光学特征对波印廷矢量变化的影响规律.

2 计算过程及分析

2.1 计算模型

将静态下的蒸发气体等效为由一定数量的蒸发颗粒组成的多粒子体系,基于忽略蒸发颗粒具体形貌特征,在对其作粗粒化处理等效为球体颗粒[25]的前提下,本计算模型选取一定体积内的颗粒作为研究对象,令蒸发颗粒等概率地随机分布在扁圆柱体内,并假设粒子的半径相同且互不重叠(见图1).高斯光束沿z轴入射,高斯波常数s=1/k ω0=0.01(k为波数,ω0为高斯光束束腰),线偏振且电场矢量沿x轴振动,定义xOz为散射平面.图2计算了在高斯光束入射(ω0=10µm)时,多粒子体系yOz平面的归一化电磁场分布.图中所选参数为球形颗粒与周围介质的相对折射率ref=1.61+0.6i,粒子尺寸参数α=0.6.另外,关于粒子的光学特征,由于有机分子颗粒在可见光范围内,折射率实部变化范围为1.0～3.0,虚部变化范围为0～0.8[26],故本工作中颗粒折射率实部与虚部取在上述范围内,为保证在一定体积内粒子不相互重叠,尺寸参数a变化范围为0.4～1.0.

2.2 主粒子数量及收敛性验证

本工作计算了在体积分数相同、粒子数不同的情况下,多粒子体系沿z轴的归一化平均坡印廷矢量分布.横、纵坐标取无量纲数,其中kz=2πz/λ,S=Sz/S0.选取主粒子数分别为2 000个与3 000个,当取定复折射率实部为1.6,虚部为0.6,尺寸参数分别为0.4,0.6和0.9时,多粒子体系沿z轴的归一化平均坡印廷矢量分布如图3所示.从图中可以发现,在体积分数相同、粒子数不同的情况下,z向平均能量都得到一定程度的衰减,且衰减的趋势呈指数分布,但粒子数的变化对z向平均能量的影响并不是十分明显.由此,本研究结果在讨论范围内较好地收敛;为减少计算量及计算时间,取2 000个粒子进行进一步研究.

图1 多粒子体系计算模型Fig.1 Computing model of multi-particle system

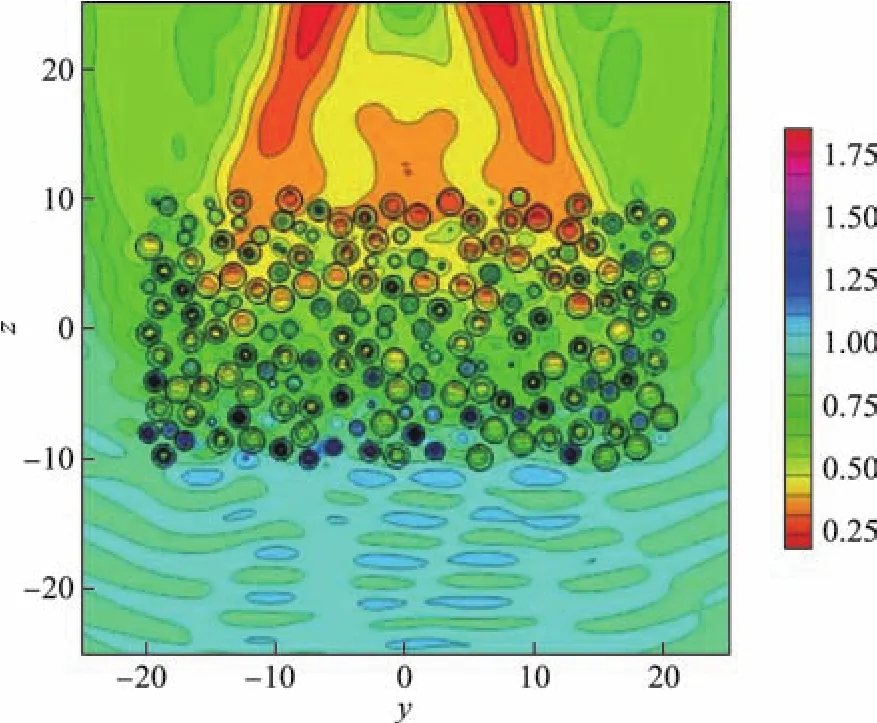
图2 蒸发颗粒体系yOz平面归一化电磁场分布Fig.2 Normalized electric f i eld of yOz plane in evaporated granalar system

2.3 粒子光学特征

粒子的光学特征主要由粒子的尺寸参数和复折射率决定,颗粒对光具有散射和吸收的作用,其折射率用复数表示如下:

式中,ε为介电常数,λ为波长,σ为导电率,c为光在真空中的传播速度.复折射率的实部β为光在介质中的传播速度与在真空中传播速度的比值;虚部γ为介质对光的吸收作用.同时,粒子大小也对光的散射和吸收有一定的影响.

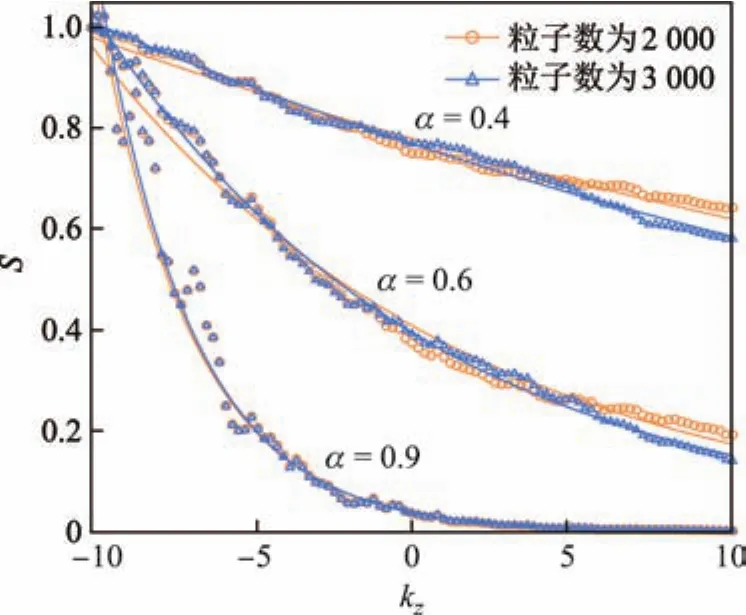
图3尺寸参数变化时不同粒子数能量衰减Fig.3 Energy attenuations at diあerent particle counts as size parameter changes

图4 分别给出了在不同光学特征情况下多粒子体系沿z轴的归一化平均坡印廷矢量分布,并用指数曲线S=exp(Akz+B)对其进行拟合.由于粒子尺寸参数与折射率对光的散射有影响,故在模型z=−10截面处光的能量也不同,即不同方程对应的B值不同.从图4(a)中可以看出,当折射率实部β取1.61,虚部γ取0.6,粒子尺寸参数α分别取0.4,0.6,0.9时,粒子的尺寸参数α越大,z向平均能量的衰减速度越快.从图4(b)可以看出,当折射率虚部γ取0.6,主粒子尺寸参数α取0.5,实部β分别取1.3,1.5,1.7时,粒子折射率实部β越小,z向平均能量的衰减速度越快.从图4(c)可以看出,当折射率实部β取1.4,主粒子尺寸参数α取0.5,折射率虚部γ分别取0.3,0.5,0.7时,粒子折射率虚部γ越大,z向平均能量的衰减速度越快.另外,对比图4(a)～(c)可以发现,在选取的光学特征范围内折射率实部对衰减速度的影响并不十分明显,而粒子的尺寸参数与折射率虚部对衰减速度的影响较大.

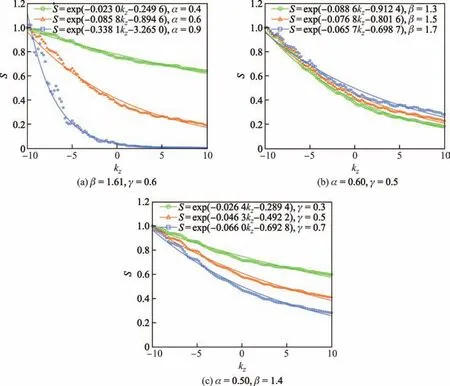
图4 不同α,β和γ值对应S的衰减曲线Fig.4 S attenuation curves corresponding to diあerent α, β and γ values

2.4 拟合分析

由前文可知,在粒子的光学特征值不同的情况下z向平均能量都呈指数衰减.接下来,任意取满足前述范围的光学特征数值来计算多粒子体系沿z轴的归一化平均坡印廷矢量,通过对尺寸参数α、折射率实部β和折射率虚部γ与拟合方程S=exp(Akz+B)中系数A,B的多元非线性回归分析,找到能反应其变化规律的关系式,进而能更好地理解粒子的光学特征对z向平均坡印廷矢量变化规律的影响.在拟合前,考虑到虚部γ与尺寸参数α对能量衰减的速度影响较大,故在拟合的过程中,以尺寸参数和虚部作为对z向平均能量影响的主体进行分析.

拟合时可以发现,能量衰减方程S=exp(Akz+B)中的系数A,B分别与颗粒折射率虚部γ和尺寸参数α3成正比,通过调研可以发现已知光学和物质作用规律如表1所示.表1中,

表1 已知光在介质中传播和衰减规律的相关工作Table 1 Related works of known laws of light propogation and attenuation in media

兰伯特吸收指数定律Ix=Ie−ax,a=4πγ/λ说明了系数A,B与颗粒折射率虚部γ的关系.另外,在全内反射测速技术中,为确定界面隐失波的基准光强I0,有实验证明荧光粒子的激发光强和粒子的体积成正比,即I(r,z)=(−(z−a)/dp).可见,在多粒子消光问题中,不考虑颗粒的浓度变化与分布规律,而只考虑各光学特征对系数A,B衰减速率的影响情况,去掉某些相关性较小的项,以γ和a3为拟合方程主体简化方程,最后整理得到光学特征与拟合系数之间的关系式

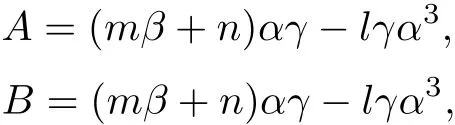
式中,各参数值的定义如表2所示.

3 回归检验

将系数A,B代入方程S=exp(Akz+B)中检验拟合效果得到Sreal与Sfit的相关性(见图5).图5中,横坐标为不同横截面处对应的z向平均坡印廷矢量的实际值Sreal,纵坐标为拟合方程计算出的对应相同截面的z向平均坡印廷矢量的拟合值Sfit.可以发现,Sreal与Sfit的对应点聚集在直线Sfit=Sreal附近,误差在10%以内.

表2 拟合公式参数值Table 2 Parameter values of f i tting coeきcients

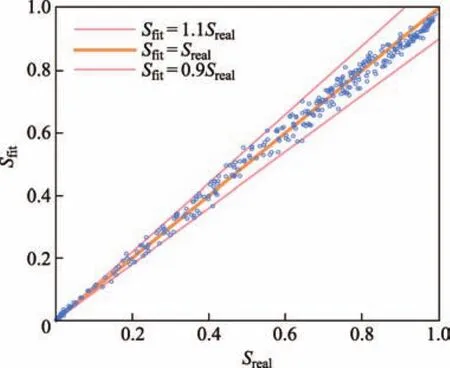
图 5 Sreal与Sf i t的相关性Fig.5 Correlation diagram between Srealand Sf i t

4 结束语

本研究以广义Lorenz-Mie理论为基础,计算了蒸发微粒多粒子体系沿入射光方向的归一化平均波印廷矢量,同时给出在不同尺寸参数与折射率情况下光轴方向能量的衰减情况,找到衰减规律与尺寸参数和折射率实部、虚部之间的联系,并给出了关系表达.研究表明:①入射光经过蒸发颗粒多粒子体系,能量沿入射方向呈指数衰减;②γα3为能量衰减的主要影响量,客观上讲光束通过球体体积的效应和其他研究所反映物理规律保持一致;③由拟合方程计算得到了y向平均坡印廷矢量值Sfit与实际坡印廷矢量值Sreal的相关性,拟合误差在10%之内,可见关系式能较好地反演计算数据.

[1]CHIANG C K,FINCHER C R,PARK Y W,et al.Electrical conductivity in doped polyacetylene[J].Physical Review Letters,1977,39(17):1098-1101.

[2]POPE M,KALLMANN H P,MAGNANTE P.Electroluminescence in organic crystals[J].Chemical Physics,1963,38(8):2042-2043.

[3]VINCETT P S,BARLOW W A,HANN R A,et al.Electrical conduction and low voltage blue electroluminescence in vacuum-deposited organic f i lms[J].Thin Solid Films,1982,94(2):171-183.

[4]CHANG Y L,SONG Y,WANG Z,et al.Highly eきcient warm white organic light-emitting diodes by triplet exciton conversion[J].Advanced Functional Materials,2013,23(6):705-712.

[5]ZHONG C,DUAN C,HUANG F,et al.Materials and devices toward fully solution processable organic light-emitting diodes[J].Chemistry of Materials,2010,23(3):326-340.

[6]JU J,YAMAGATA Y,HIGUCHI T.Thin-f i lm fabrication method for organic light-emitting diodes using electrospray deposition[J].Advanced Materials,2009,21(43):4343-4347.

[7]KOPOLA P,TUOMIKOSKI M,SUHONEN R,et al.Gravure printed organic light emitting diodes for lighting applications[J].Thin Solid Films,2009,517(19):5757-5762.

[8]LEE E.Simulation of the thin-f i lm thickness distribution for an OLED thermal evaporation process[J].Vacuum,2009,83(5):848-852.

[9]DUAN L,HOU L,LEE T W,et al.Solution processable small molecules for organic light-emitting diodes[J].Jmaterchem,2010,20(31):6392-6407.

[10]LI J,NAKAGAWA T,MACDONALD J,et al.Highly eきcient organic light-emitting diode based on a hidden thermally activated delayed f l uorescence channel in a heptazine derivative[J].Advanced Materials,2013,25(24):3319-3323.

[11]SVOBODA K,BLOCK S M.Biological applications of optical forces[J].Annual Review of Biophysics and Biomolecular Structure,1994,23(1):247-285.

[12]ASHKIN A,DZIEDZIC J,BjORKHOLM J,et al.Observation of a single-beam gradient force optical trap for dielectric particles[J].Optics letters,1986,11(5):288-290.

[13]BAUMGARTL J,MAZILU M,DHOLAKIA K.Optically mediated particle clearing using Airy wavepackets[J].Nature Photonics,2008,2(11):675-678.

[14]MARAGO O M,JONES P H,GUCCIARDI P G,et al.Optical trapping and manipulation of nanostructures[J].Nature Nanotechnology,2013,8(11):807-819.

[15]URBAN A S,CARRETERO-PALACIOS S,LUTICH A A,et al.Optical trapping and manipulation of plasmonic nanoparticles:fundamentals,applications,and perspectives[J].Nanoscale,2014,6(9):4458-4474.

[16]BUI A A M,STILGOE A B,NIEMINEN T A,et al.Calibration of nonspherical particles in optical tweezers using only position measurement[J].Optics Letters,2013,38(8):1244-1246.

[17]TSAI W Y,HUANG J S,HUANG C B.Selective trapping or rotation of isotropic dielectric microparticles by optical near f i eld in a plasmonic archimedes spiral[J].Nano Letters,2014,14(2):547-552.

[18]MIE G.Beitr¨ae zur optik tr¨uer medien,speziell kolloidaler metall¨oungen[J].Annalen der Physik,1908,330(3):377-445.

[19]GOUESBET G,MAHEU B,GREHAN G.Light scattering from a sphere arbitrarily located in a Gaussian beam,using a Bromwich formulation[J].JOSA A,1988,5(9):1427-1443.

[20]XU Y L.Electromagnetic scattering by an aggregate of spheres:asymmetry parameter[J].Physics Letters A,1998,249(1/2):30-36.

[21]MACKOWSKI D W.Analysis of radiative scattering for multiple sphere conf i gurations[J].Mathematical and Physical Sciences,1991,433:599-614.

[22]DOICU A,WRIEDT T.Computation of the beam-shape coeきcients in the generalized Lorenz?Mie theory by using the translational addition theorem for spherical vector wave functions[J].Applied Optics,1997,36(13):2971-2978.

[23]GOUESBET G,GREHAN G,MAHEU B.Computations of the g(n)coeきcients in the generalized Lorenz-Mie theory using three diあerent methods[J].Applied Optics,1988,27(23):4874-4883.

[24]GOUESBET G,GREHAN G,MAHEU B.Localized interpretation to compute all the coeきcientsin the generalized Lorenz-Mie theory[J].Journal of the Optical Society of America A,1990,7(6):998.

[25]黄凯,王志亮,周哲玮,等.蒸发微粒气体对光的消光特征[J].上海大学学报(自然科学版),2013,19(6):598-605.

[26]魏斌,吴谊群,顾冬红,等.偶氮金属螯合物薄膜的光学常数和吸收光谱[J].光学学报,2004,24(6):739-742.

[27]王曙.不透明矿物晶体光学[M].北京:地质出版社,1976:43-47.

[28]PLASS G N.Mie scattering and absorption cross sections for absorbing particles[J].Applied Optics,1965,5(2):279-285.

[29]蔡文彬,王乃岩,宋东明,等.石墨粒径对红外消光特性的影响[J].红外技术,2003,25(5):68-71.

[30]KIHM K D,BANERjEE A,CHOI C K,et al.Near-wall hindered Brownian diあusion of nanoparticles examined by three-dimensional ratiometric total internal ref l ection f l uorescence microscopy(3-D R-TIRFM)[J].Experiments in Fluids,2004,37(6):811-824.

[31]史飞,郑旭,陈荣前,等.全内反射测速技术(TIRV)中界面隐失波基准光强I0的确定[J].实验流体力学,2014,28(6):80-85.本文彩色版可登陆本刊网站查询:http://www.journal.shu.edu.cn