InAs/GaAs量子点生长的KMC模拟

陈 龙,徐凯宇

(1.上海大学上海市应用数学和力学研究所,上海200072;2.上海大学理学院,上海200444)

量子点结构是指在空间3个维度内尺寸均小于电子波长(载流子在空间各方向上均受到限制)、具有量子限域效应的3维量子受限系统[1].量子点是由半导体材料制成的纳米粒子,具有许多独特的纳米性质.由于量子点具有明显的量子约束、隧穿、干涉等光、电学效应,使其在微电子、光电子器件、超大规模集成电路以及量子计算机等方面具有较大的潜在应用优势[2-3].目前,利用分子束外延技术[4],基于Stranski-Krastanov(S-K)生长模式[5-6]的自组织生长是制备量子点的一种有效途径,制备高度有序的量子点以及研究量子点的定位生长成为研究热点.

制备空间排列有序、量子点密度高的手段有很多,而在应变弛豫图形衬底上生长量子点的方法具有可控性好、杂质较少等优点[7-8],从而受到越来越多的关注.有2种方法可以得到应变弛豫的图形衬底:①通过物理化学腐蚀在衬底表面形成沟槽;②采用埋藏量子点方法,从而在衬底表面产生应变弛豫图形.在GaAs衬底上生长InAs量子点系统中,一般会采用第2种方法,即在GaAs衬底中预先埋藏1层InAs量子点方法,而后在此衬底上进行自组织外延生长,此时岛成核位置会更倾向于埋藏量子点的正上方,从而得到有序排列的岛[9].

半导体量子点的生长通常采用的是自组织外延生长方式,其生长过程是一个复杂的热动力学过程,因此影响量子点生长的因素比较多,主要包括生长过程中的温度、沉积速率、应变能等[10].在实际制备中量子点的生长温度不宜太低,因为过低的生长温度有可能导致生成物为多晶和非晶结构[11];其次,在利用外延技术制备InAs/GaAs系统量子点的工艺过程中,原子沉积到衬底上的速率不同将对生长制备结果造成影响[12].由于沉积速率不一样,单个原子沉积到衬底表面的时间也就不一样,衬底上原子的扩散时间也不一样,沉积速率越低,扩散的时间也越充足.因此,扩散是否充分对生长过程显得犹为重要.另外,从热力学角度来看,量子点生长过程是系统能量达到最小化的过程,也是表面能与应变能相互作用和相互竞争的过程,故应变能的分布是影响半导体量子点生长的因素之一.研究结果表明,在量子点的生长过程中原子趋向于向应变能较高的位置聚集,应变能不同的分布形式将决定量子点的成型位置与形状[13],因而通过改变应变能分布可以有效控制量子点的定位生长.

考虑到量子点生长过程是一个随时间变化的随机过程,本工作运用动力学蒙特卡罗(kinetic Monte Carlo,KMC)方法,通过定义能量势垒来模拟量子点早期生长阶段单原子层成核(2D岛形成)过程[14],分析量子点的生长温度、沉积速率和埋层深度对InAs/GaAs量子点系统生长的影响.该阶段将直接影响在S-K生长模式下量子点的最终位置和大小.

1 计算模型以及温度和沉积速率对量子点生长的影响

1.1 KMC模型的建立

为了模拟量子点生长早期第1层单原子层阶段,本工作将采用全扩散SOS(solid-onsolid)模型的KMC模型,此模型中将衬底划分成离散的网格,每个沉积原子只可占据1个格点.该模型中沉积过程是任意的,也就是说原子沉积位置是随机的,而表面扩散是该模型的主要机制,此过程由原子跃迁概率控制(跃迁概率可由Arrhenius公式得到).KMC模拟过程如下:首先,沉积原子按照沉积速率随机沉积到衬底(衬底大小为LxLy,其中Lx为长度,Ly为宽度)上任意位置,如果该位置已有原子占据则重新选择1个沉积位置;然后计算出每个位置原子相对应的跃迁概率p和总跃迁概率,由此确定原子是否跃迁以及跃迁方向.取总跃迁概率的倒数为每一步的时间步长,当时间满足(式中,F为沉积速率,即单位时间内沉积到衬底表面的原子层数;t为沉积时间)时,新的原子开始沉积,重复以上步骤直至全部原子完成沉积(其模拟过程流程图见图1).

由于模拟过程为早期单原子层阶段,故模拟对象都是小覆盖率条件下的生长过程.表面覆盖率

图1 KMC模拟过程流程图Fig.1 Flow chart of KMC simulation process

原子在衬底表面的运动为热迁移过程,在本模型中原子每次只能跃迁到邻近的空位,如果邻近位置都已有原子则不跃迁.如果原子要从一个点跃迁到另一个点,由于这个过程包含了一个简单的态的转变,故其跃迁就需要克服相应的能量势垒.由跃迁理论可知,在跃迁过程中所需克服的能量势垒只取决于其初始位置,而与跃迁方向和终点位置无关.衬底表面的原子是否跃迁由其跃迁概率(只与初始位置相关)决定,跃迁概率满足Arrhenius公式:

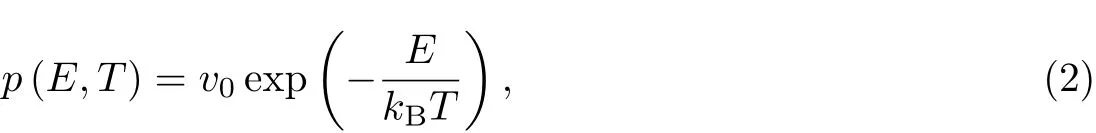
式中,v0为表面原子的尝试跃迁频率(约为1013s−1),kB为玻尔兹曼常数,T为衬底温度(生长温度),E为在跃迁过程中所需克服的能量势垒,

式中,Es为原子与衬底表面的结合能,通常为一固定常数;En为与周围原子之间的束缚能之和,

式中,n(n≤4)为周围最邻近位置的原子数,m(m≤4)为次近邻位置上的原子数.在InAs/GaAs系统中,E0=0.3 eV,表示目标原子与最近邻单个原子之间的束缚能[15];而Estr(x,y)为图形化衬底表面的应变能,应变能的分布与位置坐标相关.

1.2 温度对量子点生长的影响

对于InAs/GaAs系统而言,常见的生长制备得到的量子点通常为金字塔形,过高的温度会出现塌陷现象,量子点形状则变成圆屋顶形.另外,从热力学角度看,当温度过高时原子的热运动比较活跃,扩散比较快速,岛间距离比较分散,岛的密度会减小,不利于控制;但温度太低又不利于原子的结晶成核.同时,在实验中也可以观察到,小幅提高生长温度可获得更宽的尺寸分布和较少缺陷的量子点材料;而过高的生长温度将会导致量子点面密度降低[16].因此,本工作将通过计算机模拟研究温度对量子点生长的早期阶段的影响.

为了研究GaAs应变弛豫图形衬底上生长InAs量子点过程中温度的影响,本工作模拟了温度从350 K到700 K之间变化(每次温度变化间隔为50 K)的量子点前期单原子层生长情况.模拟中选取的模拟参数[7,15,17]为选取的图形衬底为正方形的渐变应变弛豫衬底,图形衬底大小为100×100网格化格点.根据应变能的分布衬底又划分成10×10正方形小区域,每个区域中应变能分布均为正四棱锥形式,在中间处取得最大值Estr2,在边界处取最小值Estr1.生长时间t=1.5 s,沉积速率F=0.1 mL/s,表面覆盖率为15%,即模拟中沉积原子数为1 500个,能量势垒取值为Estr1=0.35 eV,Estr2=0.55 eV,Es=0.3 eV.

图2显示了在不同温度条件下衬底上岛的生长形态.从图中可以很直观地看到,在温度很低时岛的分布比较凌乱,且岛的尺寸也较小;随着温度的升高,岛的尺寸逐步增大,逐渐出现定位清晰整齐的较大岛;当温度达到450 K时,可以看到原子分布依旧比较混乱,但已经有原子开始聚集在一起;当温度升高至600 K时,岛的分布已经比较均匀,在每个网格之内基本上都有且仅有一个岛,各个位置的岛的大小也比较一致;当温度达到650 K或更高时,虽然此时每个网格中仅有一岛,但却出现了部分尺寸较小的岛,这些小岛中的原子被一些较大岛吸引而离开,这与奥斯特瓦尔德熟化现象相符.随着进一步迁移,这些小岛可能会逐渐消失,从而使得衬底上的2D岛的分布不再有规律,岛的尺寸也会相差较大,这对于工艺上定位生长量子点或者控制制备量子点尺寸是不利的.

图2 在不同温度下2D岛的形态模拟结果Fig.2 2D island morphologies results under diあerent temperatures

通过模拟结果可以看出,温度对于衬底表面2D岛的生长影响显著.在生长制备过程中所选取的温度不宜过低,因为温度过低会导致原子的跃迁概率减小,原子在衬底表面的扩散不活跃,就不利于原子聚集;而温度过高会使原子扩散行为非常活跃,一些较小的岛上的原子容易被更大的岛所吸引,从而使得岛的形态大小分布不再均匀,同样也不利于量子点的生长,这一结论与实验结果基本吻合[15].模拟结果显示,温度在600 K左右时,2D岛的分布更趋于均匀,这表明600 K是最有利于量子点生长的温度.

1.3 沉积速率对量子点生长的影响

从温度条件的模拟结果中可以看出,扩散是否充分对生长非常重要,尤其是对于低温条件,因为此时原子运动不够活跃,很难扩散充分.那么针对低温条件,如果给予更充足的扩散时间,即更低的沉积速率是否能得到更好的结果？为此本工作将进一步研究沉积速率对生长的影响.

为了研究GaAs应变弛豫图形衬底上生长InAs量子点过程中沉积速率对其影响,本工作模拟了温度在400 K和600 K的量子点前期单原子层生长情形.模拟中选取的模拟参数:能量势Estr1=0.35 eV,Estr2=0.55 eV,Es=0.3 eV.表面覆盖率为15%,即模拟中沉积原子数为1 500个,在保持同样覆盖率条件下根据沉积速率的不同考虑2种情况:①生长时间t=1.5 s,沉积速率F=0.1 mL/s;②生长时间t=1.5 s,沉积速率F=0.01 mL/s.

由于仅考虑沉积速率的影响,故本模拟中除了沉积速率外的其他参量保持不变,使系统在沉积结束时能达到相同的表面覆盖率,即要求在不同的沉积速率下都沉积了相同数量的原子.这样,低沉积速率就需要更长的时间来完成沉积过程,而在沉积过程中扩散过程同时进行.因此,在低沉积速率的情况下沉积原子的扩散将进行得更加充分.考虑到当温度在400 K、沉积速率为0.1 mL/s时原子分布还比较混乱,只有少量原子聚集成核形成岛.图3为当温度保持400 K不变时,只改变沉积速率的2维生长模拟结果.结果表明,在沉积刚刚结束时低沉积速率情况下成岛的尺寸要比高沉积速率下成岛的尺寸更大、更均匀,且岛的分布也比较有规律,同一区域内几乎只形成一个岛.因此,当温度保持在400 K时,如果不考虑由沉积速率太慢引起的沉积过程时间过长可能造成的外在因素的影响(沉积时间过长可能使生长过程中有更多杂质成分进入,从工艺生产制备角度出发,太长的生长时间会导致效率问题),较低的沉积速率有利于2D岛聚集成核.相应地,实验结果也表明较高的沉积速率会降低量子点的质量,较低的沉积速率可以得到分布更均匀、纯度更高的量子点[12],本模拟所得到的结果与实验结果基本一致.

图3 不同沉积速率下2D岛的形态模拟结果(T=400 K)Fig.3 2D island morphologies results under diあerent deposition rates(T=400 K)

相较于图3结果,图4为在相同条件下只将生长中衬底的温度从400 K改成600 K时的情况.当温度为600 K时,无论是在低沉积速率还是高沉积速率生长结束时都出现了分布均匀的岛.从直观上看二者差别并不大,岛的分布情形基本一致,基本上每个岛都占据一个区域,二者的差别只是岛的大小略有出入.造成以上结果的原因在于,低沉积速率量子点生长比高沉积速率情形下能得到更多的沉积时间,使原子在表面的扩散能进行得更彻底,也就越容易聚集成核形成2D岛.在400 K时,高沉积速率下沉积结束时原子在表面的扩散行为并未彻底完成,而低沉积速率给了原子足够时间去扩散迁移,从而更有利于其生长;当温度在600 K时,原子的表面扩散进行得比较充分,因此无论沉积速率高还是低均能得到分布均匀的生长情形.可见,在温度较低或其他原因导致的不利于量子点生长的情形下,可以通过适当地降低沉积速率的方法得到尺寸更均匀的量子点结构.

图4 不同沉积速率下2 D的岛的形态模拟结果(T=600 K)Fig.4 2D island morphologies results under diあerent deposition rates T=600 K

2 埋层深度对量子点生长的影响

2.1 衬底表面的应变能计算

在GaAs衬底上生长InAs量子点的过程中,为了得到应变弛豫的图形衬底,通常会采用埋藏量子点的方法,即在GaAs衬底中预先埋藏一层InAs量子点,而后在此衬底上进行自组织外延生长.以上的模拟在考虑影响量子点生长因素时,应变弛豫衬底上的应变能都取定值,也就是说衬底是一样的.然而,事实上在不同的埋层深度下得到的衬底表面的应变能是不同的,大量研究也已证实应变能对于量子点的生长有着重要影响作用[10,13,17],因此需要考虑埋藏量子点的深度对应变弛豫衬底上应变能的影响,进而研究对量子点生长产生的影响.为了考虑埋层深度的影响,需要计算出在不同深度下衬底表面的应变能的分布情况及大小.如果将埋藏在衬底中的量子点看成夹杂物,即将衬底看作夹杂问题中的半无限大基底,则此问题便可以作为夹杂问题来处理.而这类各向异性非均匀夹杂问题可用格林函数法得到精确封闭形式解[18-20].

在将InAs量子点埋藏在GaAs衬底时会产生一个特征应变,该特征应变可由晶格失配度决定,InAs与GaAs的晶格失配度约为7%,故在InAs/GaAs系统中特征应变取为0.07[21-22].对于各向异性非均匀夹杂问题,在夹杂物内部存在特征应变,内外部材料参数分别为和Cijlm.如果等于Cijlm,则非均匀夹杂问题就退化成为均匀夹杂问题.

首先,用D表示基体区域,在基体区域V中有一个特征应变.假设是在无限远处施加的应力,如果材料是均质的,即没有非均匀性,则在基体区域中应变场所对应的本构关系为=.因此,一个非均匀问题,即在区域V内外部的本构关系可以根据经典的Eshelby非均匀夹杂关系得到[23-24]

式中,σij和γij为产生的应力和应变场.

引入等效特征应变概念,式(5a),(5b)能够被等价成

令

则式(6)可以被写成

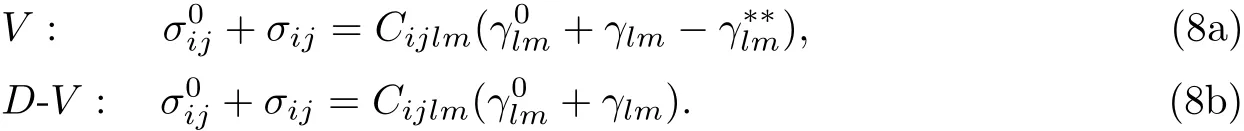
对于如上所述的特征应变问题,区域V中的应力平衡方程可表示为[25-26]

将式(8a)代入式(9)可以得到

可以清楚看到,等式(10)的右边部分代表等效体积力,可写为

式(11)即为新的特征应变与等效体积力之间的关系式.

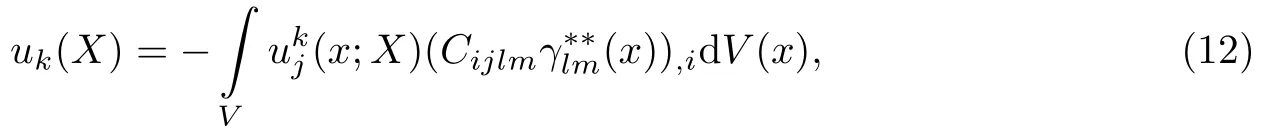
通过格林函数法可以得到夹杂区域V中任意点x(x,z)处的特征应变,在点X(X,Z)处产生的位移式中,被积函数是等效体积力与线源格林函数的乘积,x;X)为线源格林函数[19],Cijlm为GaAs材料的弹性常数.

进一步,可以得到相应的应变、应力以及应变能:

通过计算得到应变能的分布形式与之前模拟中提出的应变能分布形式近似相同,是完全对称的近似于正四棱锥形状,只是在不同埋层深度下的应变能大小不同.表1给出了在不同埋层深度下应变能的最大值Estr2和最小值Estr1.从表中可以清晰地看出,随着深度的增大,应变能的大小逐渐减小,而应变能的变化幅度也随之减小.为了简化计算量,本模拟中只改变在不同埋层深度下对应的应变能的最大值和最小值,且应变能分布形式均选取正四棱锥形.

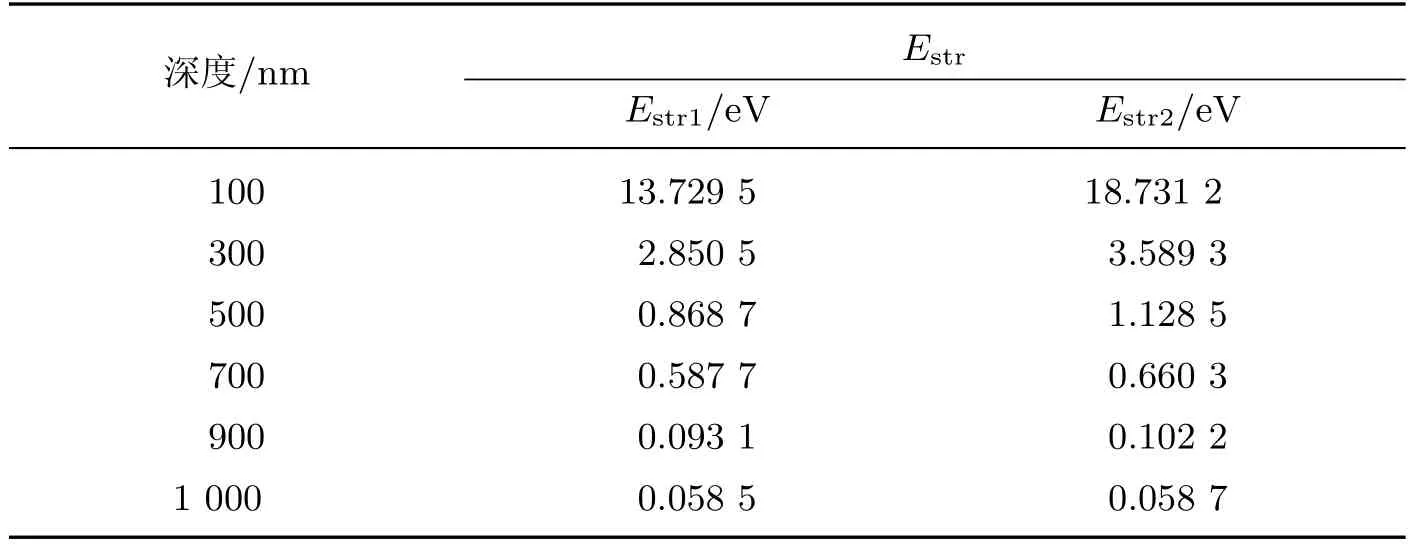
表1 不同深度下的应变能计算结果Table 1 Corresponding strain energy results under diあerent depths

2.2 模拟结果分析

在运用KMC方法模拟在GaAs衬底上生长InAs量子点的过程中,选取的模拟参数为模拟区域大小为100×100网格,整个区域又分成10×10的小区域,每个小区域上都是应变能呈正四棱锥分布的渐变的应变弛豫图形衬底形式.生长温度T=600 K;生长时间t=1.5 s;沉积速率F=0.01 mL/s;表面覆盖率为15%,即模拟中沉积原子数为1 500个;埋层深度分别为100,300,500,700,900和1 000 nm.相对应的应变能大小由表1给出.

图5为埋层深度在100,300,500,700,900和1 000 nm情况下,生长结束时的衬底上2D岛的形态.从图中可以明显看到,在埋层深度较深时,2D岛的分布比较混乱,岛的尺寸也较小,甚至在达到1 000 nm时几乎看不到成形的岛,也就是说此时量子点几乎不生长.而随着深度变浅,岛形状开始变得有规律,开始出现较大的岛,模拟中发现埋层深度在100 nm或更浅时,有些小岛会逐渐被较大的岛吸引,小岛逐渐消失,从而形成更大的岛.从模拟结果中还可以看出,深度在100,300和500 nm时都出现岛成核现象,在700 nm深度下有少量原子在聚集,但原子分布依旧比较混乱,而在900 nm或1 000 nm时并无岛形成,而2D岛的成核过程将直接影响到3维量子点的生长,这说明埋藏量子点的深度越深越不利于量子点的生长与制备.

上述结果可从计算得到的应变能角度来解释.量子点埋藏越深,其在衬底表面所产生的应变能越小且应变能的变化幅度越小,如埋层深度达到100 nm时,衬底表面的应变能大小是1 000 nm深度下应变能的200～300倍,变化幅度约为25 000倍.由式(2)可知,应变能越大跃迁概率越大,沉积原子越活跃也越容易在衬底表面迁移.由于在生长过程中量子点更偏向于向着应变能较大的位置生长,故应变能的变化幅度越大越有利于量子点的生长.而埋层深度在1 000 nm时衬底表面应变能的变化几乎可以忽略,因此在此深度下没有出现2D岛成核情况.

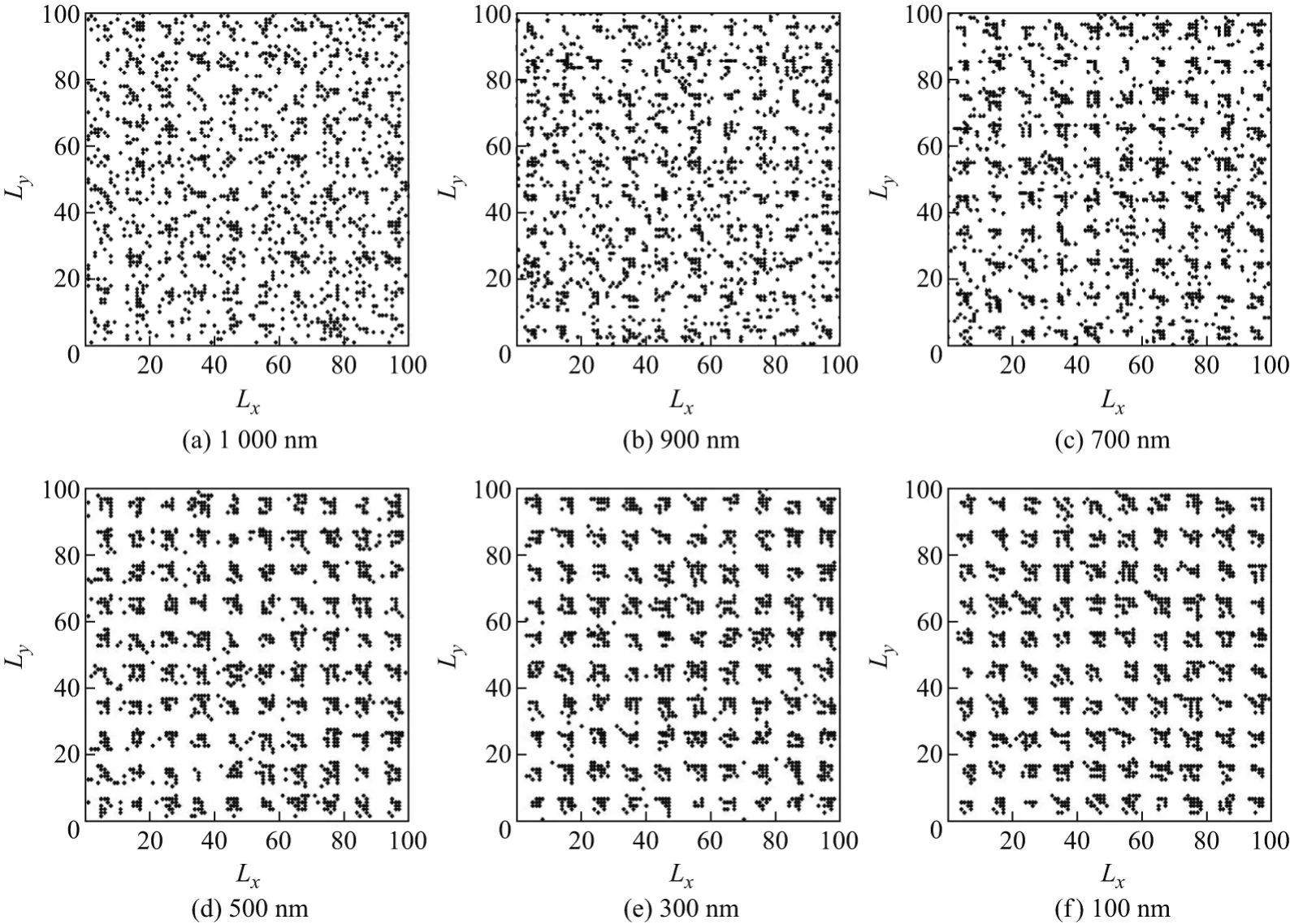
图5 不同深度下2D岛的形态Fig.5 2D island morphologies under diあerent depths

图6 不同大小岛的数量分布Fig.6 Island quantities distributions with diあerent island sizes

虽然从模拟结果中看,埋藏位置越浅越好,但也不能过浅.首先,在深度100 nm条件下已经出现部分较小的岛被较大的岛吸引的情形,从而出现小部分离散的原子,这并不利于生长大小分布均匀的量子点.图6显示不同大小岛的数量分布.从图6中可看出,相对于300 nm情形下,埋层深度在100 nm时岛的大小分布更不均匀,出现较多的大于理想尺寸的岛(岛的尺寸用岛所包含的原子数计量,理想的分布均匀的岛含有15个原子).为了衡量2D岛分布的混乱程度,本工作计算了岛的尺寸分布的标准差,标准差越小说明岛分布越均匀.计算结果发现,在100 nm情形下标准差值为4.533,而300 nm时为3.307,显然在100 nm时岛的分布比300 nm时更混乱.另外,如果埋藏的量子点位置太浅,埋藏在衬底中的量子点有可能会直接影响到沉积原子与衬底之间的结合能.当埋层深度太小时,其在衬底表面的应变能会非常大,在埋层深度为50 nm时的大小约为100 nm时的103倍.从跃迁概率式(2)可知,跃迁概率随着应变能大小呈指数级增长,此时的跃迁概率将会非常大,原子会非常活跃,从实际生长制备角度考虑,生长速度太快不容易控制应变能.

3 结束语

利用KMC方法对GaAs衬底上生长InAs量子点的过程进行了模拟,并考虑了温度、沉积速率和埋层深度对量子点生长前期单原子层阶段的影响.模拟结果显示,温度对量子点早期2D成核过程有显著影响,通过控制温度可以形成均匀有序排列的2D岛,能得到最有利于早期单原子层生长的温度为600 K左右.另外,通过控制沉积速率也能影响2D岛的聚集,在温度较低时可通过适当降低沉积速率来得到更加均匀分布的岛;而在较高温度时,可以选取较高的沉积速率来提高制备效率.埋藏量子点的深度将改变衬底表面应变能的大小,从而影响2D岛的成核过程,结果表明当埋藏过深时量子点形成的图形衬底上的应变能变小,使岛成核趋势不明显,甚至不会成核.模拟结果显示,在埋层深度介于100 nm和500 nm之间时更有利于量子点的生长,而在900 nm时沉积原子将不再聚集.这些模拟结果为制备均匀有序的量子点以及优化生产工艺提供了依据.

[1]田强,杨锡震.半导体低维体系简介[J].物理实验,2001,21(7):3-6.

[2]魏育新,陈蕊丽.InAs/GaAs量子点激光器增益特性[J].河北大学学报(自然科学版),2016,36(3):232-236.

[3]刘珂,马文全,黄建亮,等.含有AlGaAs插入层的InAs/GaAs三色量子点红外探测器[J].物理学报,2016,65(10):329-333.

[4]李树玮,小池一步,矢野满明.垂直堆垛InAs量子点材料的分子束外延生长[J].稀有金属,2004,28(1):207-209.

[5]SHCHUKIN V A,BIMBERG D.Spontaneous ordering of nanostructures on crystal surfaces[J].Reviews of Modern Physics,1999,71:1125-1171.

[6]LI X L,WANG C X,YANG G W.Thermodynamic theory of growth of nanostructures[J].Progress in Materials Science,2014,64:121-199.

[7]SCH¨OLL E,BOSE S.Kinetic Monte Carlo simulation of the nucleation stage of the self-organized growth of quantum dots[J].Solid-State Electron,1998,42:1587-1591.

[8]THANH V L,YAM V.Superlattices of self-assembled Ge/Si(0 0 1)quantum dots[J].Applied Surface Science,2003,212/213(2):296-304.

[9]ISHIKAWA T,NISHIMURA T,KOHMOTO S,et al.Site-controlled InAs single quantum-dot structures on GaAs surfaces patterned by in situ electron-beam lithography[J].Applied Physics Letters,2000,76(2):167-169.

[10]杨红波,俞重远,刘玉敏,等.影响半导体量子点生长因素的分析[J].人工晶体学报,2004,33(6):1018-1021.

[11]胡冬枝,赵登涛,蒋伟荣,等.Si(0 0 1)斜切衬底上Ge量子点的固相外延生长[J].半导体学报,2002,23(6):604-608.

[12]WANG Q,HUANG Y Q,REN X M.The inf l uence of growth parameters on the formation on InAs/GaAs by MOCVD[J].The International Society for Optical Engineering,2012(3):277-298.

[13]PAN E,SUN M,CHUNG P W,et al.Three-dimensional kinetic Monte Carlo simulation of prepatterned quantum-dot island growth[J].Applied Physics Letters,2007,91(19):193110.

[14]EVANS J W,THIEL P A,BARTELT M C.Morphological evolution during epitaxial thin f i lm growth:formation of 2D islands and 3D mounds[J].Surface Science Reports,2006,61(1/2):1-128.

[15]宋禹忻.动力学蒙特卡罗法仿真量子点生长过程的统计分析与参数优化[D].北京:北京邮电大学,2007.

[16]杨园静,涂洁磊,李雷,等.生长温度对InAs/GaAs量子点太阳电池的影响研究[J].人工晶体学报,2014,43(2):461-464.

[17]NURMINEN L,KURONEN A,KASKI K.Kinetic Monte Carlo simulation of nucleation on patterned substrates[J].Phys Rev B,2001,63(3):03054.

[18]SUN L G,XU K Y,PAN E.Irregular inhomogeneities in an anisotropic piezoelectric plane[J].Journal of Applied Mechanics,2012,79:021014.

[19]CHEN Q D,XU K Y,PAN E.Inclusion of arbitrary polygon with a graded eigenstrain in an anisotropic piezoelectric half plane[J].International Journal of Solids and Structures,2014,51(1):53-62.

[20]PAN E.Eshelby problem of polygonal inclusions in anisotropic piezoelectric full-and halfplanes[J].J Mech Phys Solids,2004,52:567-589.

[21]何菊生,张萌,肖祁陵.半导体外延层晶格失配度的计算[J].南昌大学学报(理科版),2006,30(1):63-67.

[22]吕建国,王成彪,于翔,等.薄膜的晶格失配应力分析[J].科技创新导报,2008,20:14-15.

[23]ESHELBY J D.Elastic inclusions and inhomogeneities[J].Progress Solid Mechanics,1961,2:87-140.

[24]MURA T.Micromechanics of defects in solids[M].2nd ed.Dordrecht:Kluwer Academic Publishers,1987.

[25]ZOU W N,HE Q C,ZHENG Q S.General solution for eshelby’s problem of 2D arbitrarily shaped piezoelectric inclusions[J].International Journal of Solids and Structures,2011,48:2681-2694.

[26]PAN E.Eshelby problem of polygonal inclusions in anisotropic piezoelectric bimaterials[J].Proceedings of the Royal Society A,2004,460:537-560.