基于BP神经网络模型的ADCP倾斜条件下的修正算法研究

郑威, 杨英，惠力, 鲁成杰，赵彬，杨立

(齐鲁工业大学(山东省科学院)，山东省科学院海洋仪器仪表研究所，山东省海洋环境监测技术重点实验室，国家海洋监测设备工程技术研究中心，山东 青岛 266001)

声学多普勒流速剖面仪(acoustic Doppler current profilers，ADCP)利用声学多普勒原理测量不同深度上的海流流速，是国际上认可的先进海洋仪器之一[1]。新型ADCP在海流测量基础上开发出了波浪测量能力，其中代表性的产品有挪威Nortek公司的“浪龙”以及美国TRDI公司的“骏马”[2-4]。在利用ADCP进行波浪测量时， 将其放置于水下的固定支架上，由于海底附近的海流等的影响，ADCP会发生姿态倾斜，导致波浪估计出现误差。ADCP上安装有倾斜仪，可以实时测量ADCP俯仰角、横滚角，用来进行姿态修正，TRDI公司的波浪处理软件WAVESMON在俯仰角、横滚角大于10°时进行倾斜修正[5]。研究发现，倾斜条件下影响波浪估计的因素有仪器安放深度、俯仰角和横滚角[6-7]。现有WAVESMON软件只考虑姿态角的方法是不准确的，例如当姿态角相同时，安放深度越深，波浪估计误差越大。为了提高ADCP倾斜条件下修正算法的准确性，本文将BP神经网络模型应用于分析倾斜条件下波浪估计误差与各影响因素之间的非线性关系。

1 倾斜条件下的ADCP波浪估计修正算法

1.1 波浪方向谱的估计

现有波浪测量仪器的结果一般用波浪方向谱来表达。方向谱能细致地描绘波浪能量随频率和方向的分布情况,给出波能沿各个方向传播的信息。方向谱S(f,θ)的形式可以写为方向函数G(f,θ)和频谱S(f)的乘积形式：

S(f,θ)=S(f)G(f,θ)

，

(1)

式中，f、θ分别代表频率和方向。

由线性波浪理论可知，任意两个波浪特性间的互谱等于相应波浪特性与波面间的传递函数的乘积的傅里叶变换，即

(2)

式中，k为波数；φmn(f)为测点m和测点n之间的互谱；Tm为测点m的传递函数，Tn为测点n的传递函数,xmn，ymn分别为m和n在x和y轴向上的投影距离。

式(1)左侧的互谱φmn(f)是可以计算得到的，方向谱S(f,θ)的求解是式(2)的求逆过程，因为式(1)是一非线性方程组，求解方法不是唯一的，常用的有最大似然算法、贝叶斯算法、最大熵算法，傅里叶级数展开算法等。

1.2 波浪估计修正算法

图1 倾斜的ADCP测点阵列Fig.1 Measuring points array of tilted ADCP

本文以美国TRDI公司的“骏马”ADCP为例。“骏马”ADCP采用四波束配置，4个波束和垂直方向的夹角均为20°，4个波束在水平面上的投影夹角都为90°。TRDI公司ADCP一般选取接近水面的3层12个测点阵列[8-9]。

ADCP接近水面位置处的12个测点组成了一个测点阵列，该测点阵列可用来进行波浪反演估计。如图1所示，当ADCP存在倾斜时，ADCP的4个波束1,2,3,4的位置移动到1′,2′,3′,4′，对应的ADCP测点阵列变成了一个倾斜的阵列[10]。

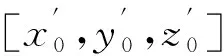
(3)

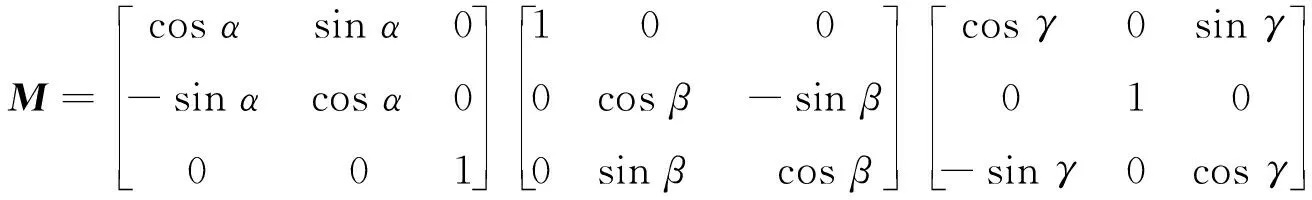
(4)

式中α,β,γ分别代表航向角、俯仰角、横滚角。由旋转矩阵的定义可知，M代表坐标转移矩阵，应该满足：

M=M-1,MMT=1

。

(5)

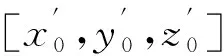
(6)

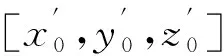
2 基于BP神经网络模型的波浪估计误差与各影响因素

2.1 BP神经网络模型

BP网络是一种多层前馈神经网络，由输入层、隐含层和输出层组成，隐含层可以有一层或多层。该网络具有较强的非线性映射能力，图2是一个典型的的BP网络结构图。x1,x2,…，xm为输入层各神经单元的实际输入；ωij为隐含层i个神经元与输入层j个神经元间的权值；g(·)为隐含层的激励函数；α1,α2,…，αq为隐含层各神经元阈值；ωki为输出层第k个神经元与隐含层第i个神经元间的权值；β1,β2,…，βn为输出层各神经元的阈值；f(·)为输出层的激励函数y1,y2,…,yn为输出层各神经元的实际输出；ek为网络的输出误差[12-13]。

图2 典型单隐含层BP神经网络结构Fig.2 Typical BP neural network with single hidden layer

BP网络结构的设计包括输入变量和输出变量的确定; 隐含层数目及每个隐含层的神经元数目的确定; 网络数据的预处理; 传递函数的选取; 训练方法及其参数的选择。BP神经网络模型的训练流程见图3。

图3 BP神经网络训练过程Fig. 3 BP neural network training process

2.2 波浪估计误差与各影响因素分析

本文应用的ADCP实测历史数据来自于美国卡罗莱纳州的实验数据，实验过程中用TRDI公司600 kHz ADCP，记录的起始时间是2008年6月22日，结束时间是2008年8月7日，超过1100组实测数据。

神经网络模型的输入值为俯仰角、横滚角和ADCP安放深度。输出值用方向谱估计百分比误差L表示。

(7)

图4选取数据段内的俯仰角、横滚角、ADCP安装深度和方向谱估计百分比误差，其中方向谱估计误差是通过商用软件分两次计算得到的，一次不考虑倾斜修正的计算值，一次考虑倾斜修正的计算值，计算二者之间的误差，即为方向谱估计误差；所选数据的俯仰角范围2°～5°，横滚角范围181.5°～185°，ADCP深度范围25.8～27.6 m，方向谱估计误差范围0%～3%。

首先，建立BP神经网络模型，输入值为俯仰角、横滚角、ADCP安装深度 ，输出值为方向谱估计百分比误差，选取前第1～700数组进行模型的训练，训练结果表明实测数据与BP神经网络模型预测数据是基本吻合的；利用训练好的神经网络模型进行仿真验证分析，并选取第700～1100组数据进行仿真验证，可以看出神经网络模型的预测值与实测值是一致的。从图4中看出，在ADCP倾斜条件下，利用BP神经网络模型可以有效地找到波浪估计误差与各影响因素之间的复杂非线性关系，实测值与 BP网络模型的预测值是吻合的。

有义波高与方向谱有如下关系：

(8)

(9)

(10)

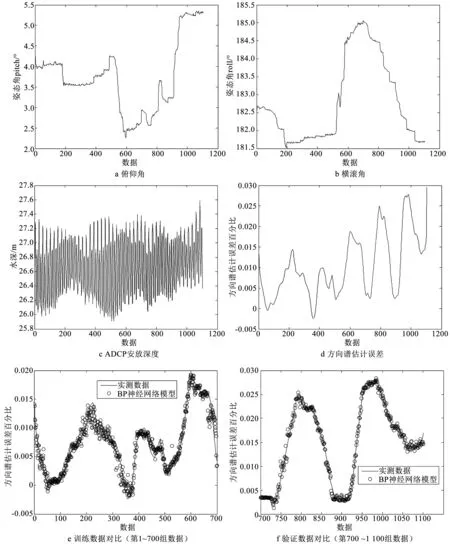
图4 实测数据与BP神经网络模型预测值的对比Fig.4 Comparison between measured data and BP neural network predicted data

现有ADCP的波高准确度一般为1%，假设波高估计误差大于1%进行倾斜修正时，根据公式(10)计算对应的方向谱估计准确度为2%，即当方向谱估计误差大于2%时，需要进行倾斜修正。

2.3 BP模型应用于倾斜修正的判断

ADCP的倾斜修正过程包括了矩阵求逆等矩阵计算，计算复杂，并不建议对于每组波浪数据进行倾斜修正。TRDI公司商用软件WAVESMON的处理流程如图5所示，通过姿态角数据来判断是否需要倾斜修正，其主要缺陷有：首先，倾斜条件下，波浪估计误差与姿态角和ADCP深度同时有关，现有算法只考虑姿态角是不精确的；其次，当姿态角大于10°进行修正，需要软件使用者在计算之前进行人工判断，并在软件上设置是否进行倾斜修正，比较繁琐。

本文的研究结果表明，BP神经网络模型可以分析找到ADCP倾斜条件下，波浪估计误差与各影响因素之间的关系，详见图6。将BP模型应用于倾斜条件下的波浪估计中，通过BP模型的预测值来判断是否进行修正，提升了波浪估计的准确性。

图5 TRDI公司WAVESMON软件处理流程Fig.5 TRDI company’s WAVESMON software handling process

图6 BP模型应用于倾斜修正Fig.6 BP neural network model applied to tilt correction

3 结论

本文将BP神经网络模型应用于研究倾斜条件下波浪估计误差与各影响因素之间的复杂非线性关系，结果表明，BP神经模型的预测值和实测值是吻合的，模型的应用是可行的。本文提出的基于BP模型的倾斜修正改进算法，提升了波浪估计的准确性。下一步将对该算法进行进一步优化，以降低算法的计算复杂度。

参考文献：

[1]刘彦祥.ADCP技术发展及其应用综述[J]. 海洋测绘, 2016, 36(2): 45-49.

[2]周庆伟，张松，武贺，等. 海洋波浪观测技术综述[J]. 海洋测绘，2016, 36(2): 39-44.

[3]DALLY W R, OSIECKI D A. Comparison of deep-water ADCP and NDBC buoy measurements to hindcast parameters[EB/OL]. [2017-03-05]. http://www.waveworkshop.org/8thWaves/Papers/N3.pdf.

[4]WORK P A. Nearshore directional wave measurements by surface-following buoy and acoustic Doppler current profiler[J]. Ocean Engineering, 2008,35(8/9): 727-737.

[5]Teledyne RD Instruments. WaveMon v3.06 User’s Guide[EB/OL]. [2017-03-05]. http://new.comm-tec.com/Docs/Manuali/RDI/WavesMon%20Users%20Guide.pdf.

[6]郑威，杨立，惠力，等. ADCP方向谱估计的倾斜修正算法研究[ J]. 山东科学，2014,27(4): 1-7.

[7]郑威，张殿伦，孙大军. 姿态传感器在坐底式ADCP波阵列中的应用[J]. 传感器与微系统，2011，30(6): 119-125.

[8]BRUMLEY B H,TERRAY E A,STRONG B S. System and method for measuring wave directional spectrum and wave height：US，6052334 [P]. 2000-04-18.

[9]KROGSTAD H E. Maximum likelihood estimation of ocean wave spectra from general arrays of wave gauges[J]. Modeling, Identification and Control. 1988, 9(2): 81-97.

[10]SCOTTI A,BUTMAN B, BEARDSLEY R C.et al. A modified beam-to-earth transformation to measure short-wavelength internal waves with an acoustic Doppler current profiler(ADCP)[J]. Journal of Atmospheric and Oceanic Technology, 2005,22(5):583.

[11]RD instruments. ADCP coordinatetransformation: Formulas and calculations[EB/OL]. [2017-03-05]. https://wiki.oceannetworks.ca/download/attach-ments/20480039/adcp%20coordinate%20transformation_Jan10.pdf?api=v2.

[12]杨茜.BP神经网络预测方法的改进及其在隧道长期沉降预测中的应用[J]. 北京工业大学学报，2011, 37(1): 92-97.

[13]崔东文.多隐含层BP神经网络模型在径流预测中的应用[J]. 水文, 2013, 33(1): 68-72.