高维随机信号THREE功率谱估计及其仿真
2015-03-09李颖
李 颖
(天津大学 理学院,天津 300072)
高维随机信号THREE功率谱估计及其仿真
李 颖
(天津大学 理学院,天津 300072)
功率谱估计是随机信号处理领域的基本问题之一,其基本方法是利用有限长的数据估计信号的功率谱.从演化进程上来看,可分为经典谱估计和现代谱估计.参照现代谱估计中的THREE谱估计方法,对基于Hellinger度量的随机信号的功率谱估计方法进行了探讨,并进行了模拟仿真.通过数值模拟,发现基于Hellinger度量的随机信号的功率谱估计方法能有效用于高维随机信号的谱估计中.
谱估计;度量;凸优化;牛顿算法
在许多工程技术、自然科学、社会经济领域中,根据观测数据来分析研究对象的周期性或能量在频域上的分布具有十分重要的意义.随机信号的功率谱反映它的频率成分以及各成分的相对强弱,能从频域上揭示信号的节律,是随机信号的重要特征.功率谱估计是利用给定的一组样本数据估计一个平稳随机信号的功率谱密度.由于实际中的随机信号长度总是有限的,用这种有限长度信号所得到的功率谱只是随机信号真实功率谱的一种估计.功率谱估计方法可以分为经典功率谱估计(非参数方法)和现代功率谱估计(参数方法)[1].经典功率谱谱估计是将数据工作区外的未知数据假设为零,相当于数据加窗.经典功率谱估计方法分为:相关函数法(BT法)、周期图法以及两种改进的周期图估计法即平均周期图法和平滑平均周期图法,其中周期图法应用较多,具有代表性.这种方法的主要缺陷是估计方差大、频率分辨率低[2-3].现代功率谱估计即参数谱估计方法则是为了克服经典功率谱估计分辨率不高,不适合短序列的处理的缺点而提出的,它是通过观测数据估计参数模型再按照求参数模型输出功率的方法估计信号功率谱.主要方法有ARMA模型、AR模型、MA模型[4-7].但是,阶数较小的AR或MA模型不能模拟具有尖锐峰和深零点的谱,而基于迭代算法的ARMA模型其全局收敛性得不到保证.
2000年,Byrnes等人为了克服ARMA模型的缺点提出了一种Byrnes-Georgiou-Lindquist(THREE)方法[8],即一种基于插值理论的高分辨率的谱估计方法.当数据量很短时,该谱估计方法也能有效地检测出谱线和谱峰现象.2003年,Ferrante等人又对该方法进行一系列的改进并推广到高维随机信号的功率谱的估计,形成了比较成熟的THREE型谱估计方法[9-13].该问题最终可转化为凸优化问题,可通过对偶理论求解.其实质是已知随机信号的先验功率谱,在功率谱密度函数距离最小的意义下使得所求的功率谱估计值尽可能地接近先验功率谱.对于一维平稳随机信号的功率谱,Tryphon T Georgiou等人于2003年把Kullback-Leibler距离应用于功率谱估计中[14],进而解决了对于给定的先验功率谱的最佳近似问题.但是把Kullback-Leibler型的距离推广到高维随机信号功率谱估计时,遇到了很大的问题[10].最近几年,Ferrante等人分别把Hellinger距离和Itakura-Satio距离应用于随机信号的功率谱近似问题中,实现了高维随机信号功率谱的估计[10, 12].
在THREE型谱估计中,主要利用拉格朗日乘数法求约束最优解.然而,对于矩阵型拉格拉日参数的求解确是比较困难的.Ferrante等人对于优化参数的求解算法主要是矩阵牛顿算法、最速下降法.基于Kullback-Leibler度量的谱估计就是利用矩阵最速下降算法求解优化参数的,而基于Hellinger度量的谱估计是利用矩阵牛顿算法求解优化参数的.本文主要对基于Hellinger距离的高维随机信号谱估计进行模拟并与其他算法进行了比较.
1 THREE功率谱估计问题及其可行性条件

THREE功率谱估计方法主要取决于下面4个要素:
1)数据{y(n),n∈Z}通过一组滤波器,它的传递函数为
G(z)=(zI-A)-1B
(1)
其中:A∈Cn×n为稳定矩阵,即它的特征值都在单位圆内,B∈Cn×n.输出为{x(n),n∈Z}即x(n+1)=Ax(n)+By(n);
2)基于y1,y2,…,yN,得到{x(n),n∈Z}的协方差∑=∑T>0的估计值∑>0;
4)衡量功率谱密度函数之间的差异性的度量S.
基于上述四点,该问题可简化为下面的有约束条件的最优化问题[10]:
minimizeS(Φ‖Ψ)

(2)
对于问题(2)可以做进一步的化简,即令
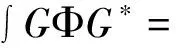
minimizeS(Φ‖Ψ)
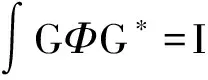
(3)
该问题即为约束优化问题,可用拉格朗日乘数法求解,其朗格朗日函数为

令δL(ΦδΦ,Λ)=0,可得最优解Φ0(Λ).如果能进一步计算出朗格朗日参数Λ,则该问题就得到了解决.但在高维随机信号功率谱的估计中,对于矩阵型拉格拉日参数的求解确是比较困难的.Ferrante等人对于优化参数的求解算法主要是矩阵牛顿算法、最速下降法.基于Kullback-Leibler度量的谱估计就是利用矩阵最速下降算法求解优化参数的,而基于Hellinger度量的谱估计是利用矩阵牛顿算法求解优化参数的.
综上所述,THREE功率谱估计方法的步骤:
Step2:
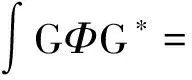
Step3:拉格朗日乘数法求解最优解:拉格朗日函数

δL(Φ,δΦ,Λ)=0⟹Φ0(Λ)
Step4:利用对偶理论对拉格朗日参数Λ的求解:其 对偶函数为JΨ(Λ)=-L(Φ0,Λ);
Step5:矩阵牛顿算法或矩阵最速下降算法进行迭代,求解最优参数Λ0,使得
minimizejΨ(Λ)=-L(Φ0,Λ).
下面介绍如何针对具体的功率谱密度函数之间的度量求解朗格朗日参数.
2 基于Hellinger距离的高维随机过程功率谱密度及其仿真
Hellinger距离是一种能够体现两个分布之间距离的度量.假设在可度量空间(Θ,λ)中,P和Q分别代表对应参数λ的两个连续分布,则这两个分布之间的Hellinger距离定义为:
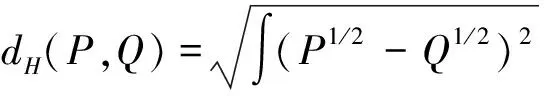
对于该度量优化参数Λ的求解是利用矩阵牛顿算法求解的.牛顿法虽然收敛速度很快,但其计算量大,对初值的依赖性很大.
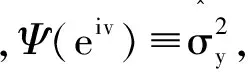
现在,考虑均值为0,方差为I的二维高斯白噪声过程通过一个平方整形滤波器得到的二维随机过程的功率谱的估计,如图1.图1分别给出随机采样100个点,功率谱估计值Φ11(ejv),Re(Φ12(ejv)),Im(Φ12(ejv)),Φ22(ejv)与真实功率谱之间的比较.由图1,我们发现基于Hellinger度量的THREE功率谱估计方法能够有效地避免谱线分裂和谱峰偏移现象,对于高维随机信号的谱估计具有很好的应用价值.
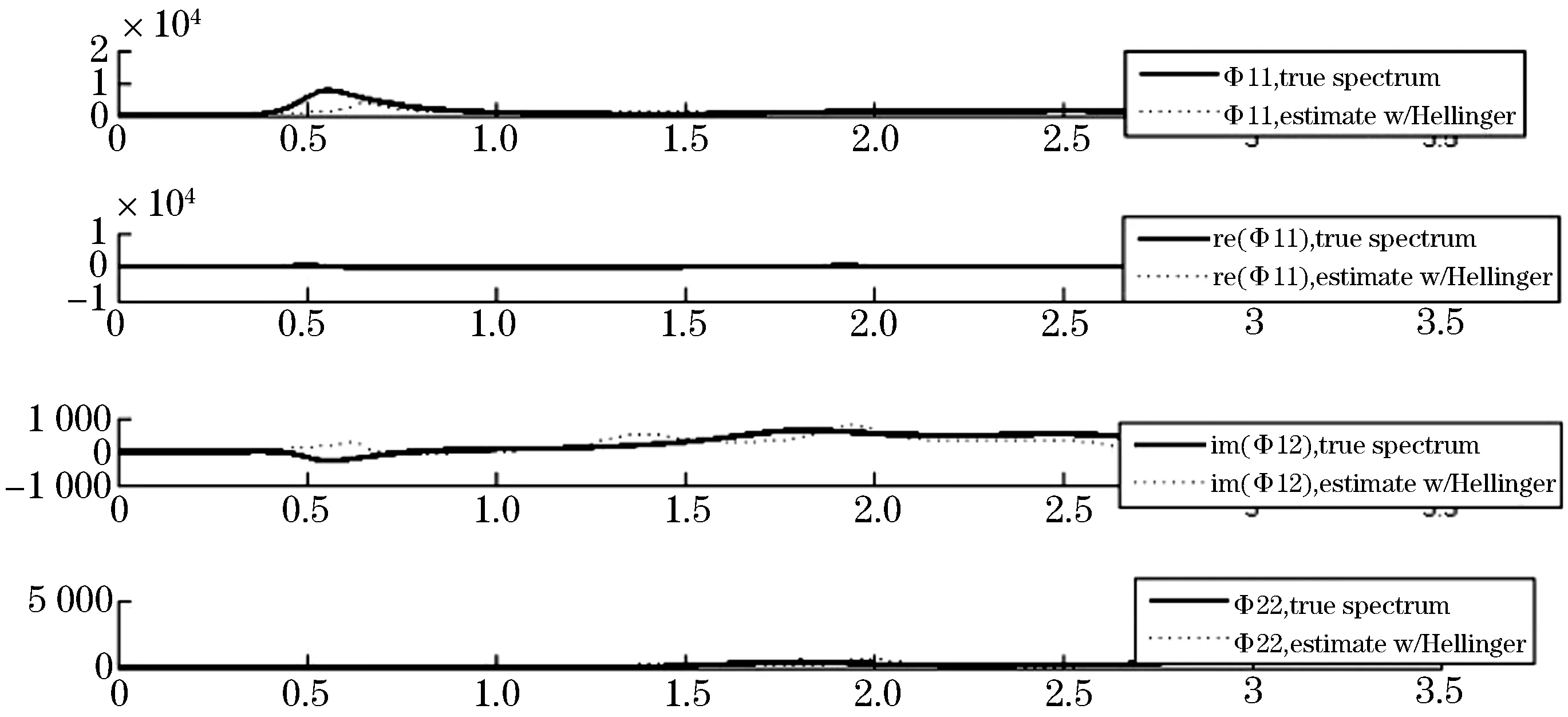
图1 功率谱估计与真实谱的比较
3 结 语
在功率谱估计中,对于一维随机信号的谱估计的研究已相当完善.随着一维现代谱估计技术的发展及实际应用中对高维随机信号谱分析的需要,国内外对高维谱估计的研究均非常重视.本文主要对现代THREE谱估计技术进行了分析并通过实验仿真.通过分析和仿真可以看出基于Hellinger度量的谱估计方法分辨率高而且估计出的谱线十分平滑.
[1] 吴仁彪, 韩 萍, 冯 青, 等译.现代信号谱分析[M]. 北京: 电子工业出版社, 2012.
[2] 伊 鑫, 曲爱华. 基于Welch算法的经典功率谱估计的Matlab分析[J]. 现代电子技术, 2010, 33(3): 7-8.
[3] 余训锋, 马大玮, 魏 琳. 改进周期图法功率谱估计中的窗函数仿真分析[J]. 计算机仿真, 2008, 3: 111-114.
[4] 廖礼彬, 邱永支, 席 斌. 一种改进的AR谱估计方法[J]. 现代电子技术, 2005,199(8): 85-96.
[5] 邓泽怀, 刘波波, 李彦良. 常见的功率谱估计方法及其Matlab仿真[J]. 电子科技, 2014, 27(2): 50-52.
[6] 王春兴. 基于Matlab 实现现代功率谱估计[J]. 现代电子技术, 2011, 34(16): 65-67.
[7] 邓卫强, 王跃钢, 杨颖涛, 等. 一种改进的 ARMA 模型参数估计方法[J]. 振动.测试与诊断, 2011, 31(3): 377-380.
[8] BYRNES C I, GEORGIOU T T, LINDQUIST A. A new approach to spectral estimation: A tunable high-resolution spectral estimator [J]. IEEE Transactions on Signal Processing, 2000, 48(11): 3189-3205.
[9] PAVON M, FERRANTE A. A new algorithm for Kullback-Leibler approximation of spectral densities[C]// IEEE conference on decision and control, 2005, 44(7): 7332.
[10] FERRANTE A, PAVON M, RAMPONI F. Hellinger versus Kullback-Leibler multivariable spectrum approximation [J]. Automatic Control, IEEE Transactions on, 2008, 53(4): 954-967.
[11] FERRANTE A, RAMPONI F, TICOZZI F. On the convergence of an efficient algorithm for Kullback-Leibler approximation of spectral densities [J]. Automatic Control, IEEE Transactions on, 2011, 56(3): 506-515.
[12] FERRANTE A, MASIERO C, PAVON M. Time and spectral domain relative entropy: A new approach to multivariate spectral estimation [J]. Automatic Control, IEEE Transactions on, 2012, 57(10): 2561-2575.
[13] PAVON M, FERRANTE A. On the Georgiou-Lindquist approach to constrained Kullback-Leibler approximation of spectral densities [J]. IEEE Transactions on Automatic Control, 2006, 51(4): 639.
[14] GEORGIOU T T, LINDQUIST A. Kullback-Leibler approximation of spectral density functions [J]. Information Theory, IEEE Transactions on, 2003, 49(11): 2910-2917.
[15] GEORGIOU T T. The structure of state covariances and its relation to the power spectrum of the input [J]. Automatic Control, IEEE Transactions on, 2002, 47(7): 1056-1066.
[16] FERRANTE A, PAVON M, ZORZI M. A maximum entropy enhancement for a family of high-resolution spectral estimators[J]. Automatic Control, IEEE Transactions on, 2012, 57(2): 318-329.
[17] ZORZI M, FERRANTE A. On the estimation of structured covariance matrices[J]. Automatica, 2012, 48(9): 2145-2151.
Simulation of multivariable spectral estimation with THREE algorithm
LI Ying
(School of Science, Tianjin University, Tianjin 300072, China)
Power spectrum estimation, one of the basic problems of random signal processing, is to use the limited length of data to estimate the power spectrum of the signal. From the point of evolution, it can be divided into classical spectrum estimation and modern spectrum estimation. This paper considered the approximation of spectra in the Hellinger sense. Simulation results indicated that it could effectively detect spectral lines and steep variations in multivariable spectral estimation.
spectral estimation; distance; convex optimization; matricial Newton method
2014-09-22.
国家自然科学基金(61379014)
李 颖(1988-),女,硕士,研究方向:多元信号谱分析.
TN911
A
1672-0946(2015)04-0506-04
