基于MATLAB的无线电信号功率谱仿真与分析
2019-04-26肖军刘洲洲
肖军,刘洲洲
(西安航空学院 电子工程学院, 西安 710077)
0 引言
无线通信发展迅猛,加速推动社会信息化,也支撑着当前的信息产业。随着无线电行业迅猛发展和壮大,该行业对现代人们的生活的影响越来越大[1]。
然而,无线电信号在信道传输的过程中会受到各种因素的干扰,有来自外部的干扰噪声,如来自太阳的干扰;在信号的发射或接收过程中,因设备自身原因,也会有热噪声;传输信道中信号也存在衰落的问题,不同信道(如瑞利信道,莱斯信道和高斯白噪声信道等)对信号的影响不同。不同信号的传输频段间传输占用不同的频段,但相互之间仍可能干扰。同一信号的不同相邻码元之间也可能存在码间干扰。诸如此类的干扰对信号的接收和检测都有一定的挑战。
信号处理中,功率谱估计是非常重要的信号分析手段。频谱模型在语音信号识别中,可了解语音是如何产生的,及语音识别、语音合成;信号的频谱在雷达和声呐系统中,能够起到声源进行定位的作用。所以信号处理研究的一个重点就是随机信号的功率谱分析。
功率谱估计的分析方法可分为经典功率谱估计法和现代功率谱估计法。经典功率谱估计分析的方差不准确,信号特性不全以及较低的分辨率。针对这些弊端,现代功率谱估计的目的就是得到较高的分辨率。以下对平均周期图法和最大熵谱估计法进行仿真比较分析。
1 经典功率谱估计之平均周期图法的分析与仿真
周期图法所得到的功率谱在大多数情况下得到的结果不理想,于是采用分段平均和加窗平滑进行改进。
分段平均则是对信号均分成K段,设每个数据段为
xin(i=0,1,…,K-1),每个数据段长度为M,n取值范围为0,1,2,…,M-1,如此,每个数据段的周期图为[2]式(1)。
(1)
再对每个数据段所得周期图的均值作为功率谱估计,即式(2)。
(2)
在此方法的基础上,巴特利特(Bartlett)提出把随机信号,长度为N,均分为长度为M的K段信号。记每个子信号为xin=xn+iM,(n=0,1, …,M-1;i=0,1, …,K-1),先对每个子信号求周期图,再求平均,可得[3]式(3)。
(3)
上式称为是Bartlett周期图,又称之为Bartlett法。
在MATLAB[4]R2014a中仿真实现平均周期图法和最大熵谱估计法的功率谱估计。假设基带信号mt=Acos(2πfmt+θ),fm=2×105Hz,其中,A∈高斯分布,0≤2πfmt+θ≤2π且均匀分布。载波信号为st=cos(2πfct),fc=6 MHz。同时假设二进制随机序列为数字基带信号[5],载波信号为c(t)=cos(2πft),f=2 MHz或c1(t)=cos(2πf1t),f1=4 MHz。基带传输速率均为2 MHz,采样频率fs=20 MHz,采样点数为N=2 048。信噪比SNR=40 dB。
与周期图法相比较,分段平均法得到的功率谱方差变小,但降低了分辨率。在此基础上,把相邻的两段数据段之间重合一部分,能改善旁瓣性能。对每个分段数据加窗平滑,可更好地旁瓣性能,但代价则是主瓣变宽。
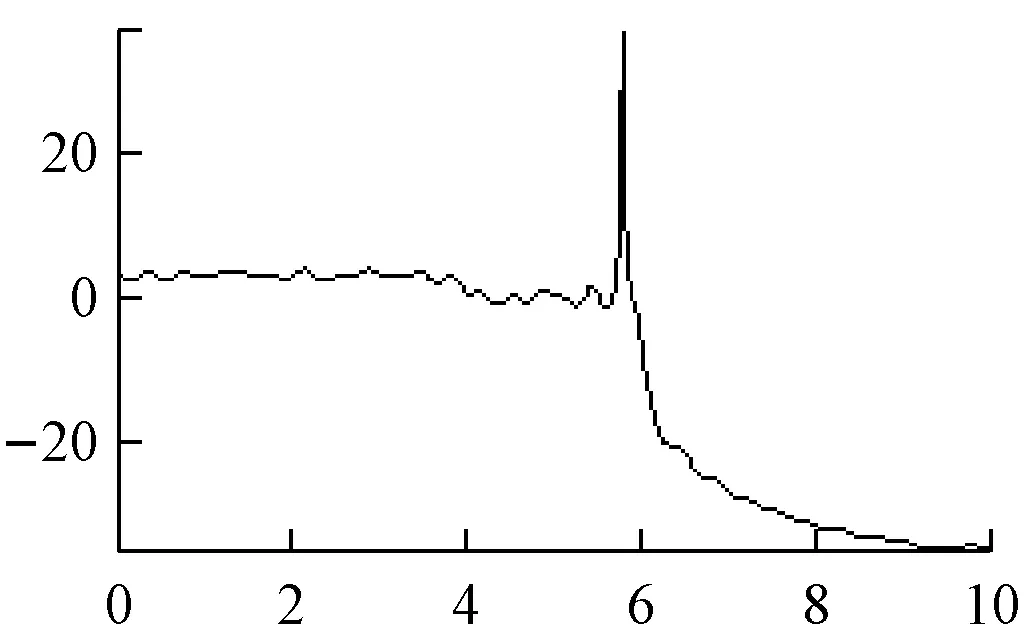
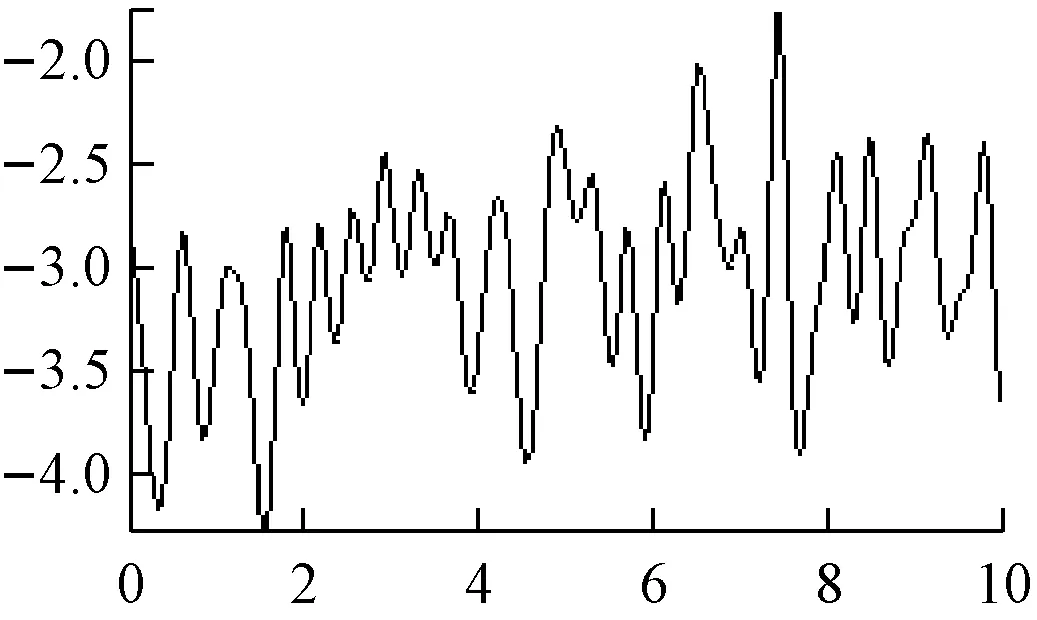
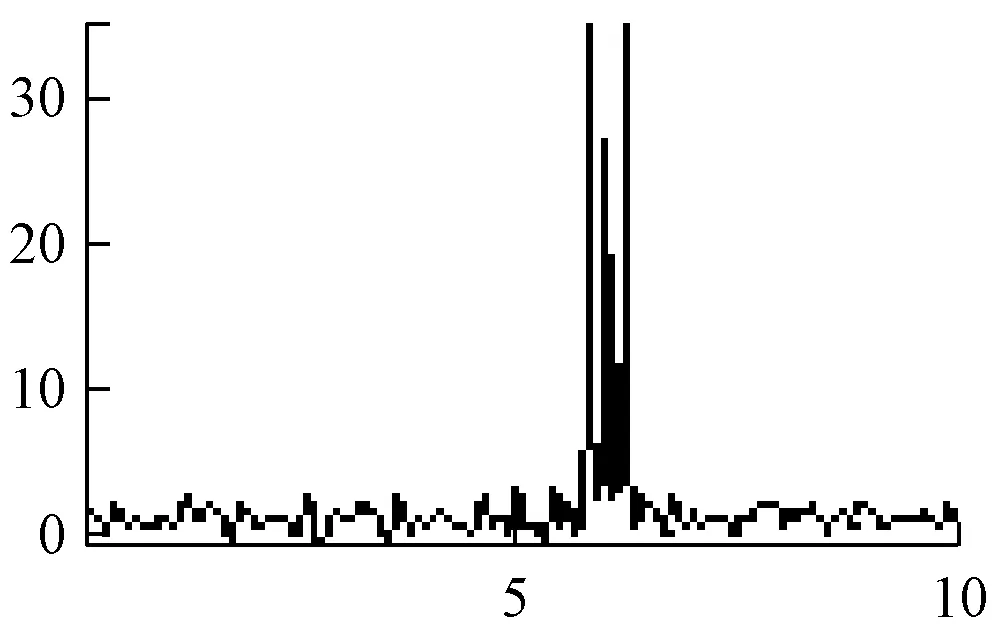
平均周期图法的功率谱估计,如图1所示。
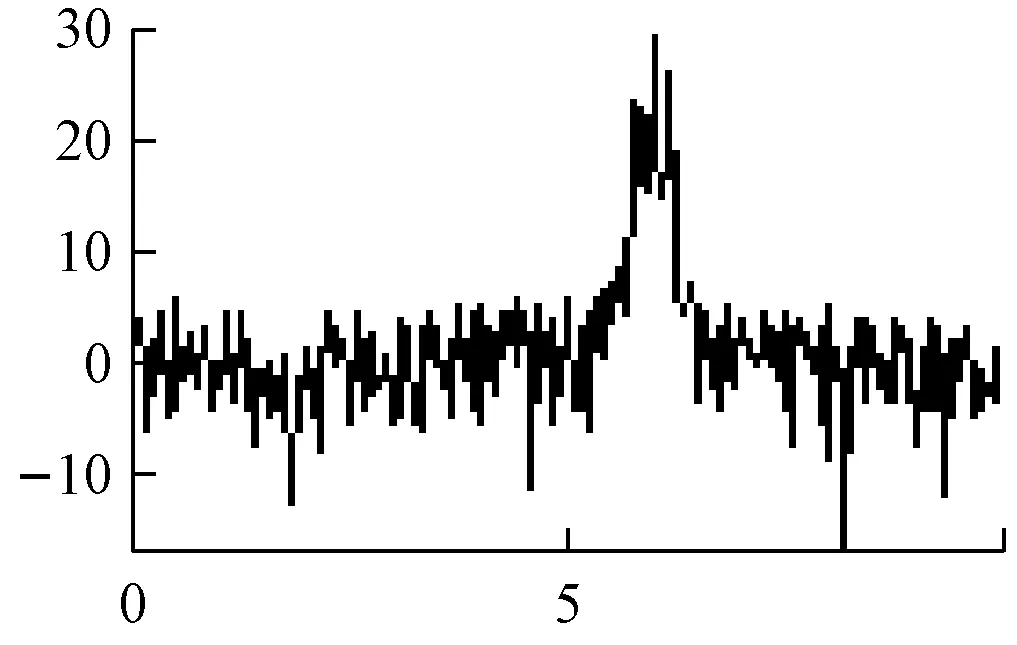
a 是AM信号
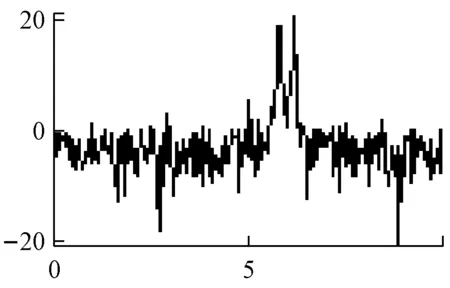
b 是DSB信号
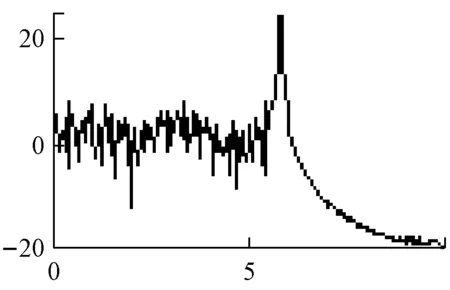
c 是SSB信号
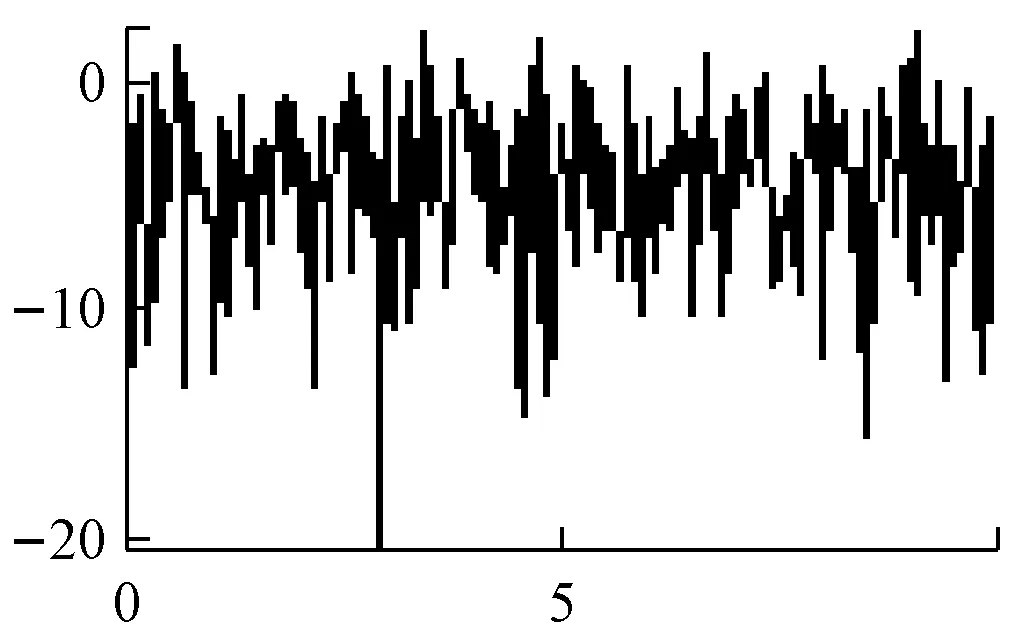
d 是FM信号
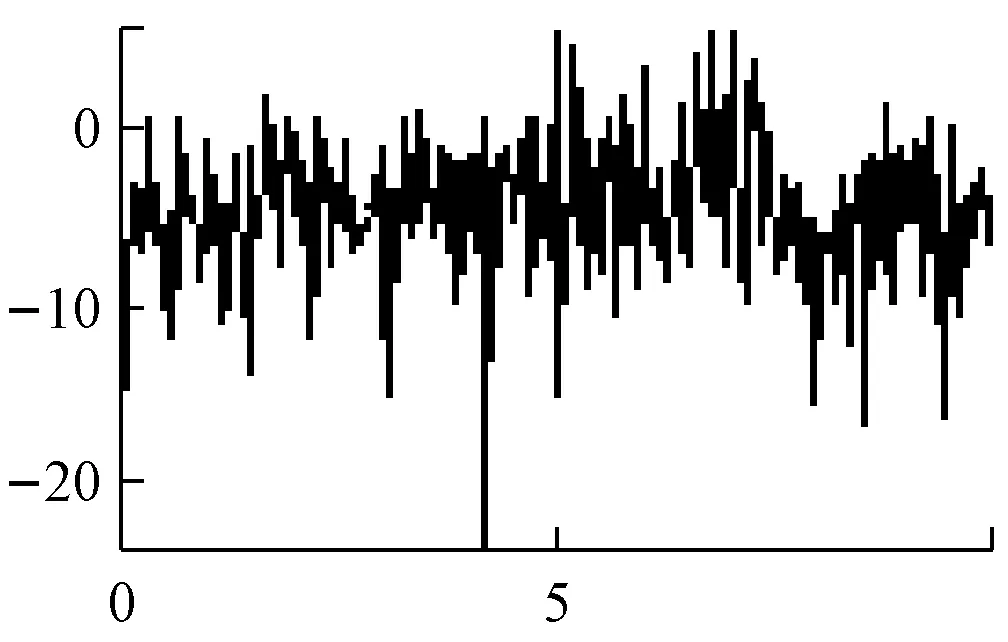
e 是PM信号

f 是2ASK信号

g 是2FSK信号
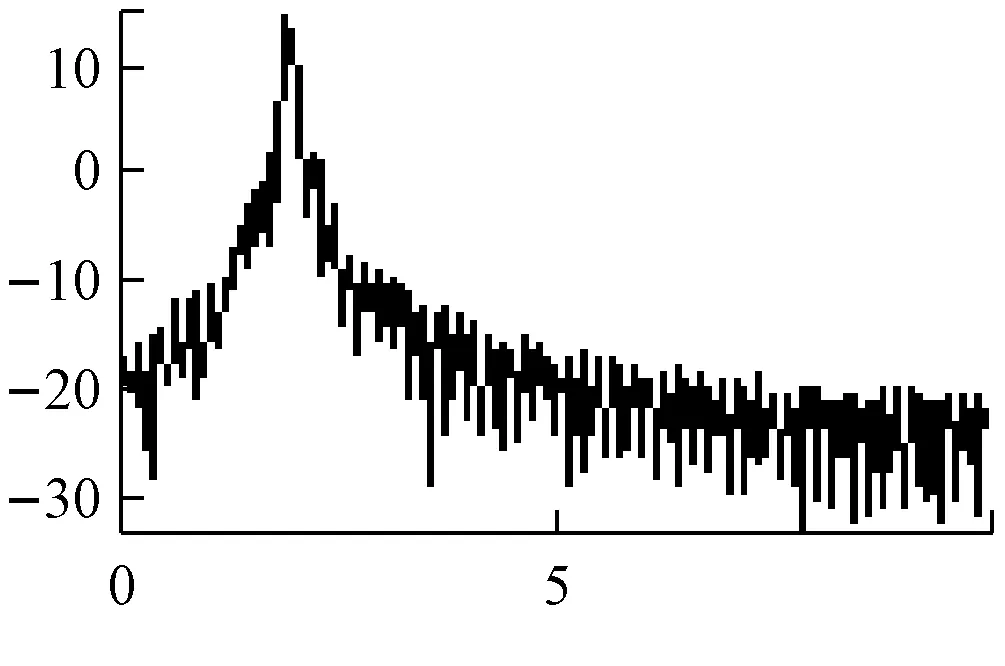
h 是2PSK信号
图1 平均周期图法谱估计
主瓣变宽,频率分辨率下降,谱线起伏更大。
2 现代功率谱估计之最大熵谱估计法分析与仿真
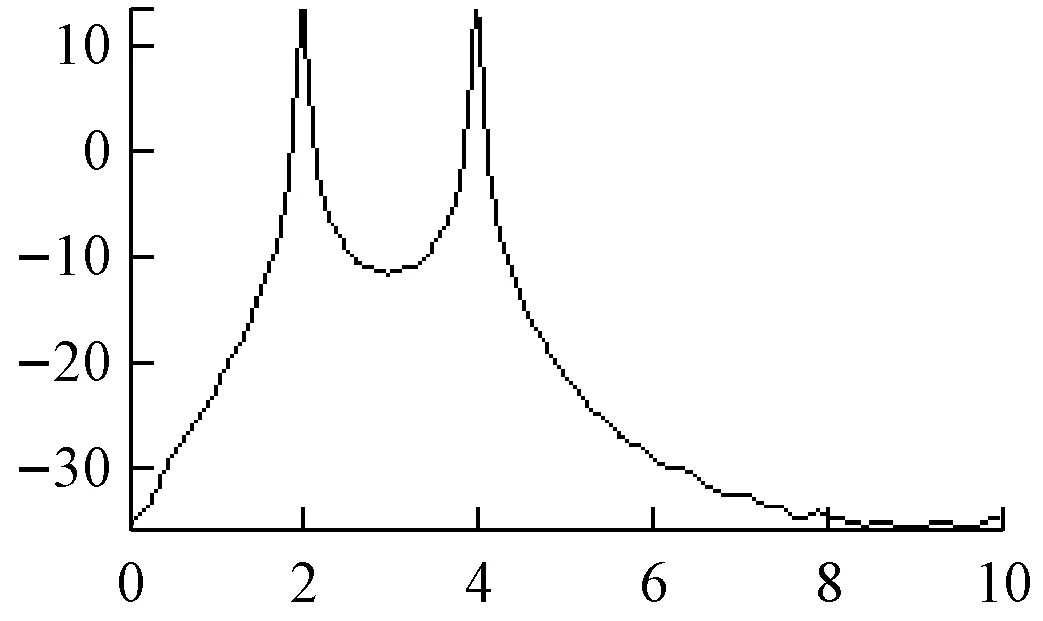
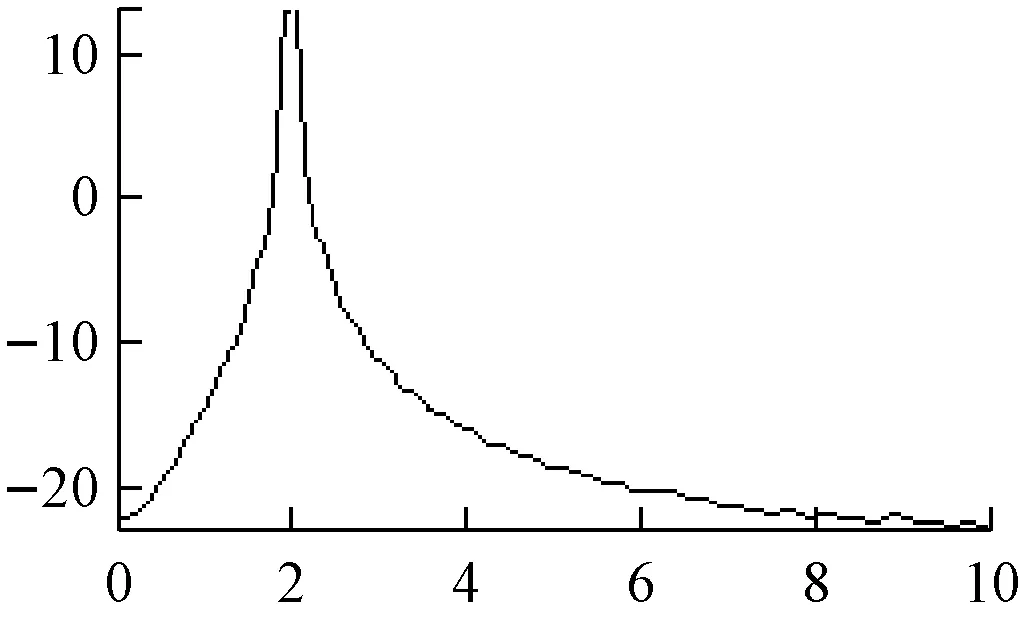
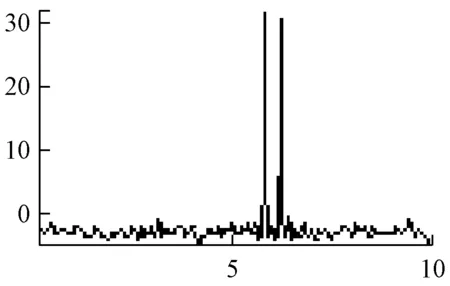
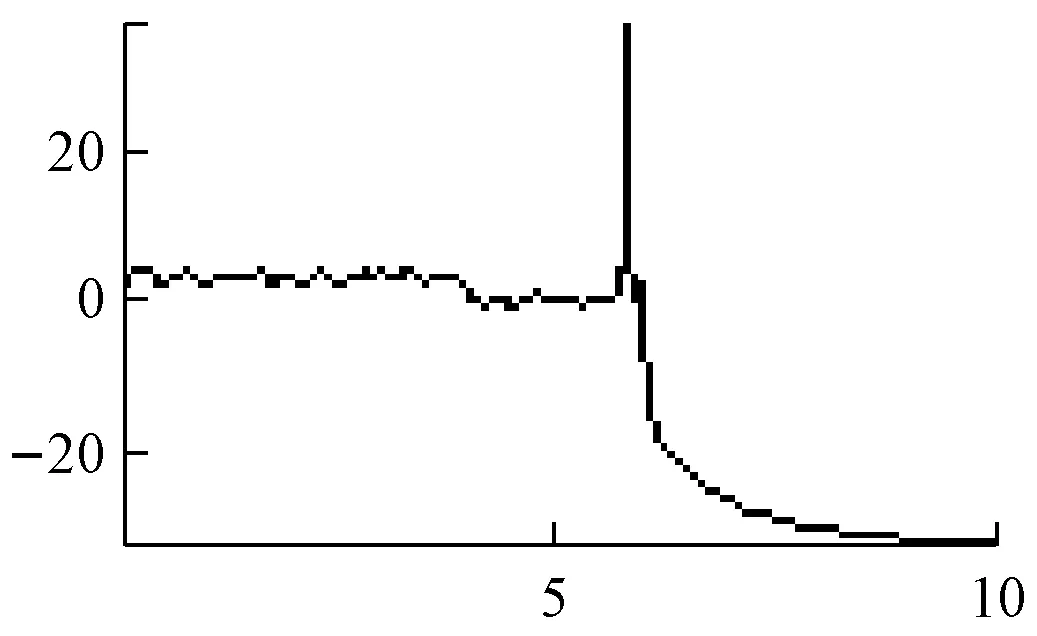
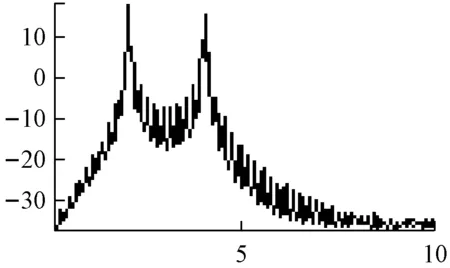
模型阶数p的选择在AR模型中非常重要。在实际中,需预先选定模型阶数k,当k 在最大熵谱估计中,滤波器的阶数不是先验的,一定要选择合适的阶数。最优值阶数可由以下三种选取准则判断 ① 最终预测误差(FEP)准则为式(4)。 (4) (阶数为M,信号采样点数为N,最优值阶数为(4)式的极值点。) ② 信息论准则(AIC)为式(5)。 (5) 最优值阶数为(5)式取最小值时的M。与最终预测误差(FEP)准则存在以下关系为式(6)。 (6) ③ 自回归传递函数准则(CAT)为式(7)。 (7) 最优值阶数为(7)式取最小值时的M。 最大熵方法的原理就是根据已知的序列,在没有任何新的假设的情况下,合理的预测未知延迟离散时间上的相关序列值,能改善因对自相关序列加窗而导致的功率谱估计性能下降。当观测向量是高斯平稳信号时,最大熵谱估计等价于AR(p)模型的参数估计法[7-9]。 从最大熵原理进行谱估计: (8) 由上式可推出RxM+1。并以此类推得到其他的自相关函数值。所以最大熵谱为式(9)。 (9) 最大熵谱估计法的分辨率随序列的长度增加而增加,解决了旁瓣泄露问题。但对信噪比极为敏感,在低信噪比下,没有对FFT的优越性,如图2和图3所示。 a 是AM信号 b 是DSB信号 c 是SSB信号 d 是FM信号 e 是PM信号 f 是2ASK信号 g 是2FSK信号 h 是2PSK信号 图2 最大熵谱估计(p=60) a 是AM信号 b 是DSB信号 c 是SSB信号 d 是FM信号 f 是2ASK信号 g 是2FSK信号 h 是2PSK信号 图3 最大熵谱估计(p=105) 通过MATLAB仿真对经典频率谱估计之平均周期图法和现代频率谱估计之最大熵谱估计法的分析,得到的平均周期图法的谱估计主瓣变宽,频率分辨率下降,谱线起伏更大。最大熵谱估计法提升了谱估计的分辨率。并通过设置AR模型中模型阶数p,可选择最优值阶数,解决了旁瓣泄露问题。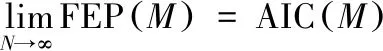







3 总结
