多轴变幅应力状态下连杆微动疲劳全寿命研究

汪玲玲 何柏岩

天津大学机构理论与装备设计教育部重点实验室，天津，300354

0 引言

微动（fretting），指名义上相对静止的两固体，其相互接触的表面在法向压力作用下相互挤压并产生往复相对滑动的现象［1⁃3］。微动疲劳作为微动损伤的主要模式，在工程实际中广泛存在且危害性大［4］。连杆作为柴油机运动部件的重要组成部分，结构形状和受载状况都比较复杂，其主要失效形式为连杆体与连杆盖配合面间的微动疲劳损伤，严重影响连杆使用寿命［5］。某些重型机械设备中的连杆部件需由海外进口，价格昂贵，检修时间不严格容易造成连杆无法修复而提前报废，占用大量使用维修费用。由于常规寿命设计方法不能满足关键性零部件的安全性和经济性要求，故需要不断探索能够有效预测微动疲劳寿命、准确确定构件检修周期的理论方法。

国内首次将连杆齿形配合面的失效与微动疲劳损伤联系起来研究的是西南交通大学摩擦学研究所的周仲荣［6］教授。SON等［7］针对柴油机连杆齿形配合面微动损伤问题进行连杆多体动力学分析和有限元分析，并利用Ruiz准则对微动疲劳裂纹所在位置以及材料点开裂可能性大小进行预测。HE等［8］对连杆齿形配合面材料成分、力学性能及损伤形貌等进行试验分析，结合准动态有限元技术，分析连杆齿形配合面出现微动疲劳裂纹的根本原因，并提出改进措施。崔海涛等［9］针对圆弧端齿结构三维微动疲劳试验难度大、成本高等问题，提出一种二维等效加载方案，设计并实现了微动疲劳试验加载装置，为微动损伤机理分析和微动疲劳寿命预测提供试验数据支持。

目前，由于微动疲劳的多轴疲劳特性，其寿命计算方法主要基于多轴疲劳临界面判别准则［10］。朱如鹏等［11］对微动疲劳中的力学参数进行分析，基于微动损伤综合参数和Ruiz准则建立了一种低周及高低周复合微动疲劳寿命预测模型。古远兴等［12］结合断裂力学理论提出了一种基于微动综合参数和断裂力学理论的混合寿命预测模型，得出裂纹尺寸和寿命之间的关系。

基于断裂力学理论的损伤容限法是计算疲劳裂纹扩展寿命的有效方法，其理论基础是PARIS等［13］给出的在恒幅加载条件下描述宏观裂纹扩展速率的Paris公式。TANAKA［14］针对多轴疲劳裂纹问题，提出有效应力强度因子概念，并将Paris公式中的应力强度因子幅用有效应力强度因子幅替代。HADDAD等［15］提出本质裂纹长度a'，得到短裂纹尖端应力强度因子幅计算表达式。NEW⁃MAN等［16⁃17］运用小裂纹理论验证裂纹闭合模型描述裂纹萌生和早期短裂纹扩展速率以及预测疲劳寿命的能力，从而得出断裂力学方法可进行疲劳裂纹形成寿命分析计算的结论。PUGNO等［18］在研究中推广Paris公式至短裂纹扩展阶段，为使用断裂力学理论进行结构全寿命分析开辟了新思路。在国内，殷之平等［19］基于Pugno理论，利用现有材料应力寿命曲线试验数据，并定义一个裂纹长度影响因子as来修正Paris公式，积分得到可用于恒幅加载条件下结构全寿命分析的SN⁃Paris综合模型。

然而，近五年有关连杆微动疲劳的研究表明，大部分学者将精力放在连杆微动损伤成因研究、连杆配合面齿形结构改进、微动疲劳试验研究以及有效减缓连杆配合面微动损伤措施的探索上，极少数学者关注连杆微动疲劳全寿命计算方法的研究。另外在微动疲劳寿命的计算方法上，多轴疲劳临界面法由于涉及到许多难确定的材料常数而给寿命预测带来困难。基于Ruiz参数的寿命计算方法依赖于研究对象和大量微动疲劳试验，耗时费力且不具普适性。损伤容限法能够给出裂纹尺寸和疲劳寿命之间的关系，并对损伤开始和停止的界限做出明确规定，但其初始缺陷尺寸依赖于无损检测技术且必须局限于疲劳裂纹宏观扩展阶段才可准确计算寿命。对于一些重要零部件，其裂纹一旦萌生或尺寸很小时就已被视为不合格，需要定期进行检修维护，因此亟需一种能够同时预测裂纹萌生寿命和扩展寿命且方便工程应用的通用方法。SN⁃Paris全寿命综合模型将损伤容限理论推广至疲劳裂纹萌生阶段，可计算结构裂纹萌生至失效断裂的全寿命，并且所用参数取决于常用的疲劳、断裂材料常数［19］，但由于大多数机械结构几何形状复杂，其局部多处于多轴应力状态，而该模型仅适用于单轴恒幅应力状态，故在工程应用中仍受到限制。

本文基于更一般结构应力状态，提出一种适用于多轴变幅应力状态下的疲劳全寿命计算模型。

1 修正Paris公式

利用断裂力学理论进行寿命计算的基础是弹塑性断裂力学的Paris公式［20］：

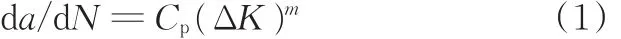
式中，a为裂纹尺寸；N为载荷周期循环次数；da/dN称为疲劳裂纹扩展速率，表示交变应力每循环一次裂纹长度的平均增量，是应力强度因子幅ΔK的函数；Cp、m都是材料参数，对于同一种材料，二者不随构件的形状和载荷性质改变，只与材料类型和应力比R有关。

式（1）表示疲劳裂纹的扩展速率与应力强度因子幅有关，应力强度因子是反映裂纹尖端应力场强弱的物理量。

变幅疲劳应力下的疲劳裂纹扩展速率取决于应力变程，而不仅仅与最大应力和最小应力之间的差值有关。研究表明［21］，对于稳定的随机变幅载荷，可以用应力强度因子范围的均方根值ΔKrms来描述疲劳裂纹的扩展速率：

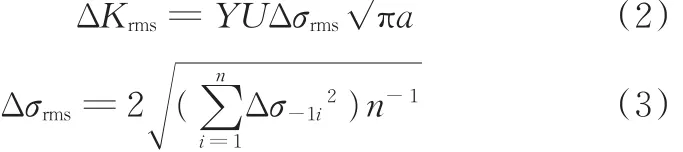
式中，Δσrms为应力范围的均方根值；i为雨流计数法处理后的第i级循环；n为循环总数；Δσ-1i为应力比为⁃1时第i级循环的应力幅；Y为与裂纹情况有关的系数，可通过查询应力强度因子手册确定数值；U为裂纹闭合影响因子，表示循环载荷压缩应力对疲劳裂纹扩展速率的影响。

裂纹闭合的影响因子主要与应力比有关，当应力比满足-1＜R＜0.7时，可利用ELBER［22］通过薄板和厚板实验所得公式进行计算：

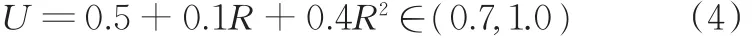
对于Ⅰ、Ⅱ型复合裂纹问题，参考文献［14］中有效应力强度因子幅理论，结合式（2）推导得到多轴变幅应力状态下有效应力强度因子幅均方根值与Ⅰ型和Ⅱ型应力范围均方根值的关系为

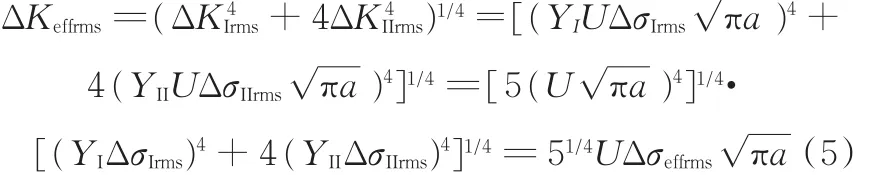
式中，ΔσIrms和ΔσIIrms分别为Ⅰ型和Ⅱ型应力范围的均方根值；YI和YII为Ⅰ型和Ⅱ型裂纹形状影响因子；Δσeffrms为Ⅰ、Ⅱ型应力复合作用下有效应力范围的均方根值。

最终对Paris公式中的应力强度因子幅进行进一步修正，得到适用于多轴变幅应力状态下疲劳裂纹扩展寿命计算的修正Paris公式及其积分式：

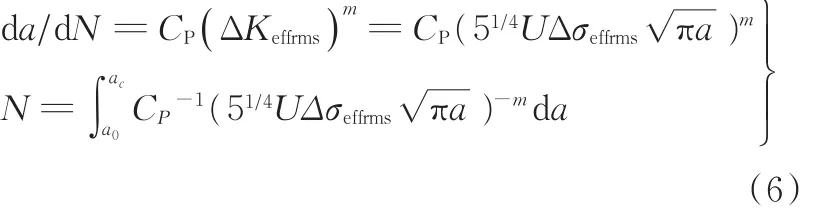
若已知裂纹初始尺寸a0和裂纹临界尺寸ac，则可由多轴变幅应力下Paris公式的积分式得到疲劳裂纹扩展寿命的计算式。

临界裂纹尺寸ac遵守线弹性断裂力学K准则，它表示应力强度因子K达到材料断裂韧性KIC时，截面有发生脆断的可能，临界裂纹尺寸可按下式计算：

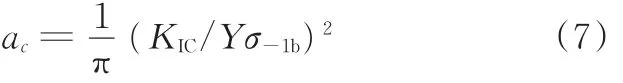
式中，KIC为断裂韧性；σ-1b为疲劳强度极限。

同理，对于初始裂纹尺寸a0，应力强度因子K达到疲劳裂纹扩展门槛值Kth时，有

2 利用S⁃N寿命曲线估算Paris公式中的材料参数

材料参数Cp、m与材料类型、裂纹情况和应力比R有关。文献［23］表明Ⅰ型应力在疲劳裂纹扩展阶段起主要控制作用，可用纯Ⅰ型应力状态下的疲劳裂纹扩展速率参数来保守估算多轴应力状态下的疲劳裂纹扩展速率参数Cp、m值。于是，可将式（1）变形得到

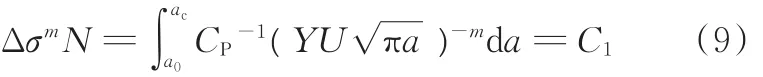
式中，Δσ为恒幅应力幅；C1在结构形式、材料类型及载荷施加方式等确定的情况下可认为是常数。

当应力比R=-1时，恒幅应力幅Δσ与应力最大值 σmax满足 Δσ= σmax，传统 Paris公式变形得到的公式与S⁃N寿命曲线拟合公式的幂指数形式以及二者对数式具有相同的形式：

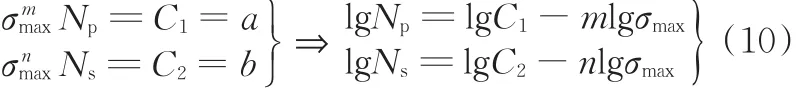
式中，Np为传统Paris公式中的载荷循环次数；Ns为S⁃N寿命曲线拟合公式中的载荷循环次数。在物理意义的描述上，前者描述裂纹宏观扩展阶段，后者描述裂纹从萌生到失稳断裂演变的全过程，两者具有重合部分，故两式对等可得到CP、m的计算表达式，即

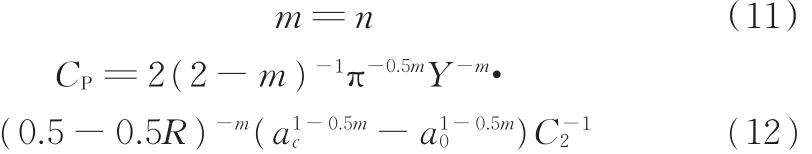
由此可以明确，确定材料常数CP、m的关键在于得到材料或零件的S⁃N曲线，从而得到S⁃N寿命曲线的幂指数形式拟合公式的系数C2和指数n的值。

3 多轴变幅应力作用下的疲劳全寿命模型

参考文献［17］和文献［18］的理论思想，引入短裂纹修正尺寸ad来进一步修正Paris公式,得到

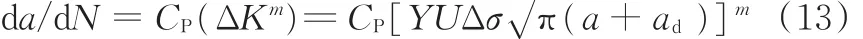
使其适用于短裂纹阶段疲劳裂纹扩展速率的描述，并积分得到寿命公式：

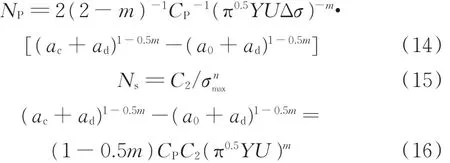
由于ad是个极小量，故当a0无限趋近于0时，所得寿命近似等同于结构从无裂纹到断裂失效的全寿命，具有和S⁃N寿命曲线相同的物理意义，即满足Npa0→0=Ns。依据此等式关系联立式（14）和式（15）求解，可得到应力比R=-1的ad的表达式。式（16）表明，短裂纹修正尺寸ad与载荷状态无关。

最终得到适用于多轴变幅应力状态下疲劳裂纹全寿命模型的一般形式为

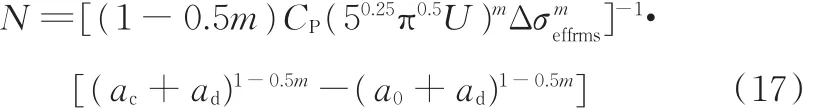
根据文献［4］中所述微动疲劳的基本理论，该模型主要考虑两种切向力作用：一种是由接触正应力引起的配合面间摩擦剪切应力作用，引起平行于配合表面的裂纹萌生扩展，导致脱层失效；另一种是垂直于裂纹面的切向拉应力作用，切向拉应力又是平行于紧密配合表面且在材料单元体前后、左右两相互垂直方向上拉应力的合力，它引起裂纹在深度方向上垂直于配合面扩展。根据应力作用效果，摩擦剪应力作为Ⅱ型应力、切向拉应力作为Ⅰ型应力被应用于全寿命模型进行结构微动疲劳全寿命研究。

4 连杆算例

4.1 连杆探伤试验

针对某海洋平台柴油发电机组连杆失效问题，表1是连杆工作24 000 h（约2.7年）之后的切口啮合齿部分探伤记录，它表示裂纹最易萌生位置集中于连杆体大端短臂齿形配合面上第二道齿根与螺栓孔相交的位置（图1a），并且检测到该处裂纹尺寸在1～1.5 mm之间。

表1 连杆工作24 000 h之后的切口啮合齿部分探伤记录Tab.1 Dectection record on con-rod mating surfaces after 24 000 working hours.

根据断裂力学理论，裂纹类型按裂纹受力情况可分为张开型（Ⅰ型）、滑开型（Ⅱ型）和撕开型（Ⅲ型）三种类型。Ⅰ型裂纹扩展拉应力垂直于裂纹面，裂纹沿作用力方向张开，沿裂纹面扩展。Ⅰ型扩展最危险，断裂韧性较差，最容易引起脆断。

为了得到连杆大端短臂齿形配合面上图1a所示裂纹处的断口形貌，需要用线切割的方式切割图中的试样得到含有裂纹的长条区域，在试验机上缓慢平稳加载横向拉力直至其断裂分开，如图1b所示，此断裂属于张开型断裂，受Ⅰ型应力强度因子控制。

图1 连杆试样Fig.1 Con-rod specimen

如图2中疲劳裂纹扩展方向所示，裂纹早期扩展方向并非完全垂直于配合面。这是由于Ⅱ型应力强度因子在裂纹萌生和早期扩展过程中起主要控制作用。综上，连杆损伤问题属于ⅠⅡ型应力作用下的微动疲劳裂纹萌生和扩展问题。

图2 裂纹扩展方向Fig.2 Crack propagation direction

4.2 连杆材料断裂韧性测定试验

断裂韧性KIC是当代工程设计中用于衡量材料抵抗裂纹失稳扩展能力的重要基本参数，是材料本身属性。本方法使用预置疲劳裂纹的缺口试样，在拉伸或三点弯曲加载条件下，将裂纹嘴张开位移V和载荷P的试验结果自动记录下来生成P⁃V曲线；按标准［24］规定的方法，在P⁃V曲线上求出裂纹长度表观扩展量为2%的载荷，并代入相应试样的断裂韧性KIC表达式以计算KIC的条件值Kq；如果试验结果满足本方法规定的有效性判据Kq=KIC，则试验结果成立，否则，试验结果无效。

根据文献［8］对连杆材料的化学成分分析试验，判断连杆材料为35CrMo。根据断裂韧性试验国标规定，断裂韧性试验试样尺寸及断裂韧性试验试样实体见图3。试验设备及试验过程见图4。

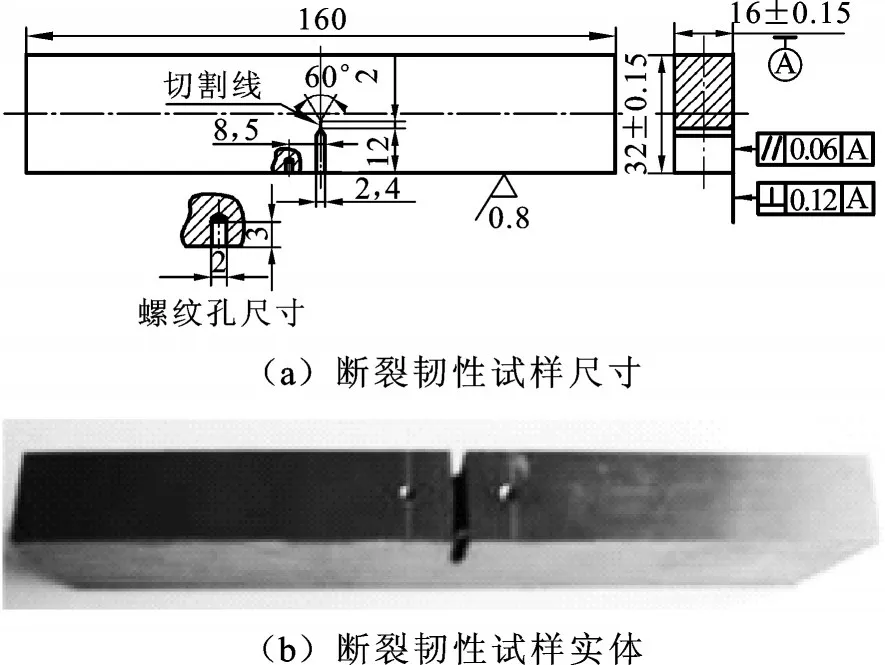
图3 断裂韧性试样Fig.3 Fracture toughness specimen

图4 断裂韧性试验设备和试验过程Fig.4 Fracture toughness test device and process

根据记录的P⁃V曲线，求得材料的断裂韧性KIC，试验的检验报告见表2。由表2中数据可知，试样2断裂韧性最小，试样3最大，试样1裂纹扩展量最大。因此，试样3抵抗裂纹扩展的能力最强。最终将实验结果平均值27.9 MPa·m1/2作为连杆材料断裂韧性。

4.3 危险节点疲劳应力谱的获取和处理

根据文献［8］进行连杆三维有限元分析，得到连杆有限元全局模型的分析结果。由于齿形面应力分析结果的正确性关系到寿命预测的准确性，因此，为了得到更精确的齿形面区域应力结果，按照有限元分析软件ABAQUS子模型功能的操作方法将全局模型切分，仅保留连杆短臂齿形配合面部分；修改边界条件，删除子模型以外的所有约束和接触关系；最后将网格数量由原来的182 523提高至356 394。图5为连杆运行一个工作周期之后其大端短臂齿形配合面子模型的Mises等效应力云图。云图表示应力集中区域主要位于第二道齿根与螺栓孔相交的位置，并按箭头所示齿向在第二道齿根均匀取点，编号1，2，…，101。

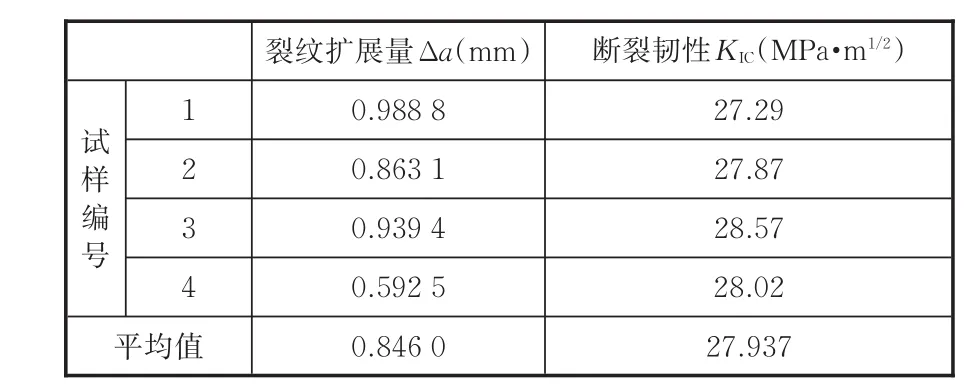
表2 断裂韧性试验检验报告Tab.2 Test report of fracture toughness test

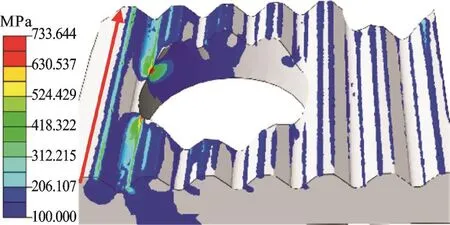
图5 连杆体大端短臂齿形配合面Mises等效应力云图Fig.5 Mises stress nephogram on short-arm toothed mating surfaces on a con-rod big end

利用有限元分析结果，可得到连杆运行一个周期各节点切向拉应力和摩擦剪应力变化情况，分别作为Ⅰ型和Ⅱ型疲劳应力谱用于连杆齿形配合面全寿命理论计算中。

图6所示是连杆大端短臂齿形配合面上第二道齿根各节点Mises等效应力、Ⅰ型应力和Ⅱ型应力的统计结果。结果表明，Mises等效应力和Ⅰ型应力最大值均发生在节点38上，Ⅱ型应力变化情况复杂，但也在节点38附近应力幅达到最大值。此节点位于第二道齿根与螺栓孔交汇处，与连杆探伤试验中所记录裂纹位置一致。故以危险节点38为计算对象，提取该节点应力状态，从而得到该节点一个周期内的Ⅰ型和Ⅱ型应力变程。用雨流计数技术将变幅应力变程转化为包含几个全循环和半循环的恒幅应力，得到表3所示的计数结果。结果表明，一个周期载荷块内的Ⅰ型和Ⅱ型应力变程曲线均可转化成一个全循环和两个半循环的恒幅疲劳应力。

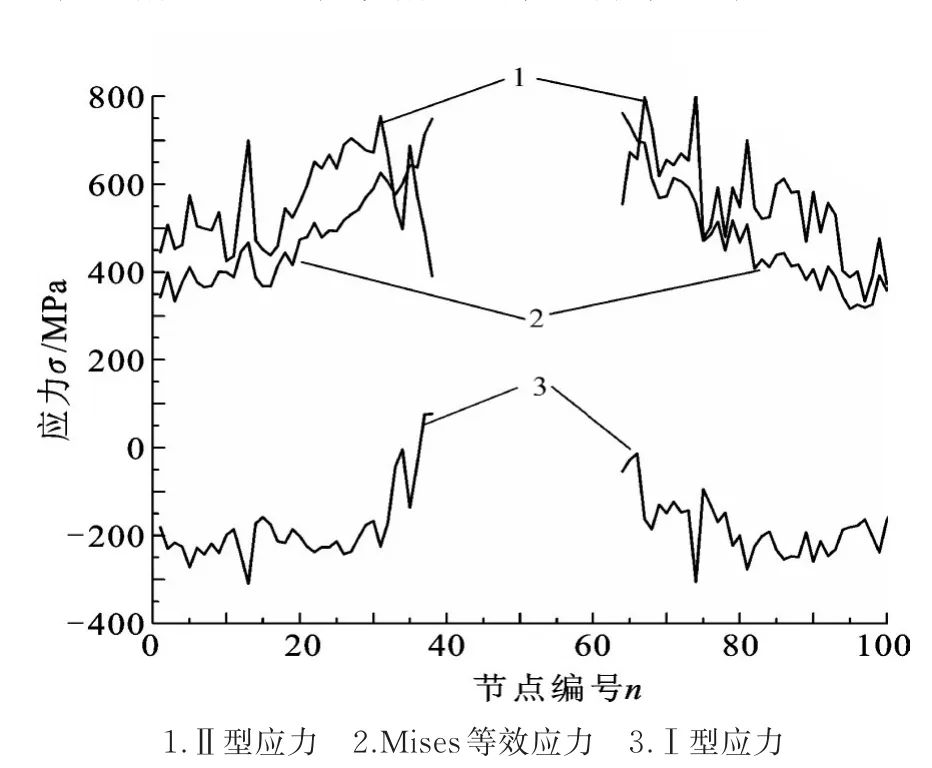
图6 连杆齿形配合面应力统计Fig.6 Stress statistics on con„rod toothed mating surfaces

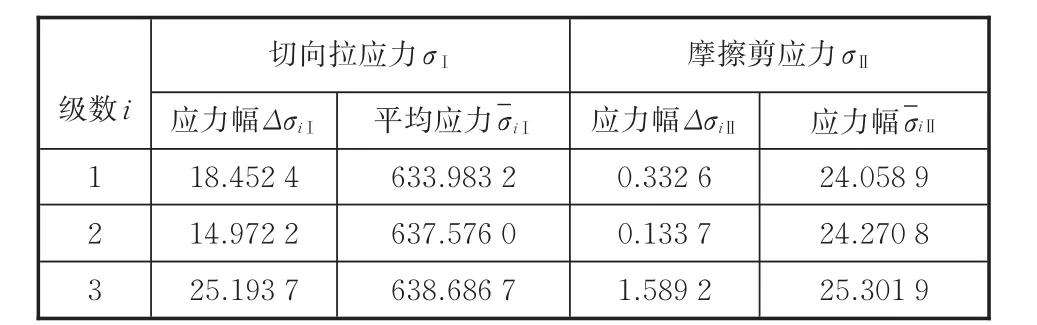
表3 雨流计数结果Tab.3 Rain flow counting results MPa

为方便应力结果服务于整个寿命计算过程，对雨流计数结果进行Goodman修正，将应力比统一为-1，修正结果见表4。将各循环部分的应力幅按照式（3）转化成Ⅰ型、Ⅱ型应力幅的均方根值（表4），代入全寿命公式中即可以进行寿命计算。

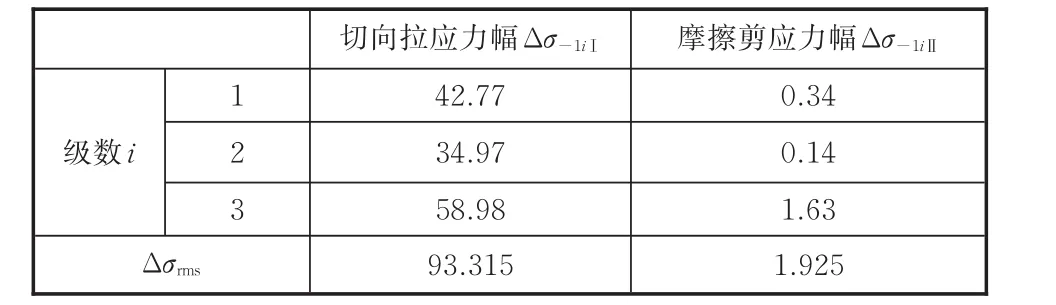
表4 疲劳应力谱处理结果Tab.4 Fatigue stress spectrum treatment resultsMPa

4.4 全寿命计算

由断裂韧性试验结果可知连杆材料断裂韧性为27.9 MPa·m1/2，由文献［25］得到35CrMo疲劳裂纹扩展门槛值为5.642 7 MPa·m1/2。根据文献［8］所提供的连杆材料机械特性试验结果可知，强度极限和屈服极限分别为876.47 MPa和715.57 MPa，可估算得到连杆S⁃N疲劳寿命曲线（图7）以及n=5.874，C2=5.4954×1019。根据此结果，通过第2节所述Paris公式中材料参数的表达式，计算得到m=5.874，CP=4.6304× 10-19。参考文献［21］，对于材料为35CrMo的圆柱光滑试样，其疲劳强度极限σ-1b和强度极限σb满足σ-1b/σb=0.467，从而估算得到疲劳强度极限为409.311 MPa。将连杆齿形配合面结构裂纹近似为矩形板孔边裂纹，由文献［26］查得裂纹形状影响因子YI约为1.09、YⅡ约为0.3。按照式（4）计算得到应力比R=-1时的裂纹闭合影响因子为0.8。基于上述结果，根据式（16）计算得到短裂纹扩展的修正尺寸ad=4.504×10-3mm。最终根据多轴变幅载荷作用下的复合型疲劳裂纹全寿命计算公式（式（17）），定义初始裂纹尺寸a0=0，按照连杆24 000 h检修周期所测裂纹尺寸设定临界裂纹尺寸ac=1.0mm。计算结果表明,当裂纹尺寸达到1 mm时，工作周期次数达到8.13×108次，所用时间约为3.0年，与损伤统计结果相比误差约为12.82%，误差主要来源于疲劳裂纹扩展参数的估算误差以及分析研究过程中的计算误差，在对精度要求高时，疲劳扩展参数可通过疲劳试验测算。对于发生高周疲劳损伤、表面状态良好的连杆件，裂纹萌生寿命在其疲劳寿命中占主导，以0.01 mm（一个晶粒尺度）作为裂纹萌生尺寸，计算所得裂纹萌生寿命为7.30×108次（2.78年），约占全寿命的89.79%。若裂纹存在初始组织缺陷0.001 mm，使用寿命则约为2.1年，且随初始缺陷尺寸的增大而减小。

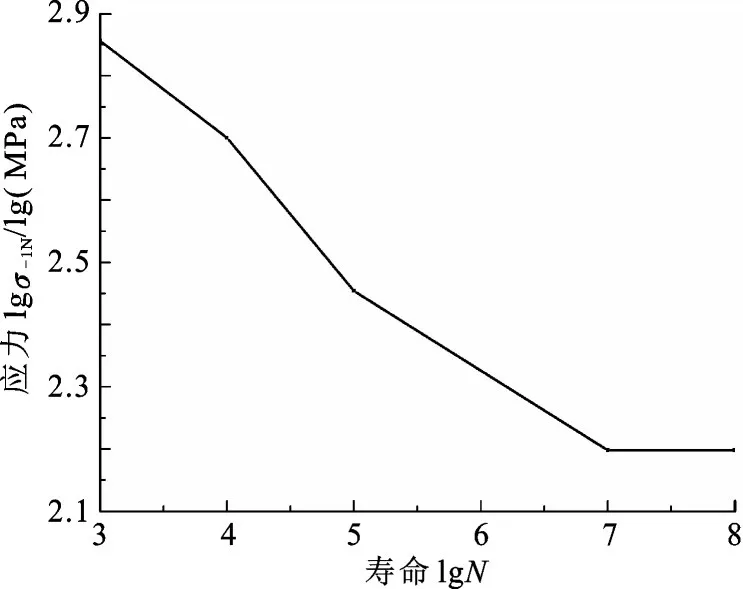
图7 连杆S-N寿命曲线Fig.7 Con-rod stress life curve

5 结论

（1）本文提出一种可用于多轴变幅疲劳应力作用下结构Ⅰ、Ⅱ复合型疲劳裂纹全寿命计算分析模型。该模型适用于多轴变幅应力载荷条件下的疲劳寿命计算，且所含材料参数均可由现有材料疲劳性能数据估算得到，亦可退化成常规Paris公式用于单轴恒幅应力条件，形象直观，且应用范围广泛。

（2）全寿命模型考虑了裂纹形状和结构构型以及压应力下裂纹尖端闭合对疲劳裂纹扩展速率的影响，从而简化了复杂结构裂纹尖端应力强度因子的求解过程，计算效率得以提高，方便工程应用。

（3）全寿命模型能够按照设定的裂纹状态进行寿命预测，不仅可以考虑初始缺陷的影响，还可根据工程实际对重要零部件安全性、可靠性要求，将临界裂纹尺寸定义成寿命设计需要满足的尺寸，可以进行结构裂纹从任意初始裂纹尺寸扩展到任意临界裂纹尺寸的寿命计算。

（4）全寿命计算结果与连杆探伤试验统计结果吻合较好，能够有效预报连杆寿命，从而有利于工程中制定严格的检修和报废处理计划，避免因检修时间不准确产生的一系列安全和经济问题。

［1］ WATERHOUSE R B，FOROULIS Z A.Fretting Cor⁃rosion［J］.Proceedings of the Institution of Mechanical Engineers，1973，169（4）:1157⁃1172.

［2］ WATERHOUSE R B.Fretting Fatigue［J］.Materials Science&Engineering，1976，25（1）：201⁃206.

［3］ 傅国如，张峥.失效分析技术［J］.理化检验：物理分册，2005，41（4）：212⁃216.FU Guoru，ZHANG Zheng.Failure Analysis Technol⁃ogy［J］.Physical Testing and Chemical Analysis Part A：Physical Testing，2005，41（4）：212⁃216.

［4］ 何明鉴.机械构件的微动疲劳［M］.北京：国防工业出版社，1994：31⁃140.HE Mingjian.The Fretting Fatigue of Mechanical Components［M］.Beijing：National Defence of Indus⁃try Press，1994：31⁃140.

［5］ 闫德顺，张仕才.16V280ZJ型柴油机连杆故障分析及处理措施［J］.内燃机车，2000（9）:31⁃33.YAN Deshun，ZHANG Shicai.Failure Analysis and Treatment Measures of a Connecting Rod of Model 16V280ZJ Diesel Engine［J］.Diesel Locomotives，2000（9）:31⁃33.

［6］ 周仲荣，朱旻昊.复合微动磨损［M］.上海：上海交通大学出版社，2004：221⁃234.ZHOU Zhongrong，ZHU Minhao.Fretting Fatigue Damage［M］.Shanghai：Shanghai Jiaotong University Press，2004：221⁃234.

［7］ SON J H，AHN S C，BAE J G，et al.Fretting Damage Prediction of Connecting Rod of Marine Diesel Engine［J］.Journal of Mechanical Science&Technology，2011，25（2）：441⁃447.

［8］ HE Baiyan，SHI Guangda，SUN Jibing，et al.Crack Analysis on the Toothed Mating Surfaces of a Diesel Engine Connecting Rod［J］.Engineering Failure Anal⁃ysis，2013，34：443⁃450.

［9］ 崔海涛，李爱民，温卫东.圆弧端齿结构微动疲劳试验加载装置的设计及实现［J］.中国机械工程，2016，27（22）:3020⁃3024.CUI Haitao，LI Aimin，WEN Weidong.Design and Implementation of Fretting Fatigue Test System for Curvie Couplings［J］.China Mechanical Engineering，2016，27（22）：3020⁃3024.

［10］ 霍永忠，尹东，赵杰江，等.微动磨损与微动疲劳寿命的计算与分析方法［J］.力学季刊，2015，36（2）：165⁃178.HUO Yongzhong，Y IN Dong，ZHAO Jiejiang，et al.Calculation and Analysis Method of Fretting Wear and Fretting Fatigue Life［J］.Chinese Quar⁃terly of Mechanics，2015，36（2）：165⁃178.

［11］ 朱如鹏，潘升材.高低周复合载荷作用下微动疲劳寿命预测研究［J］.机械强度，1996，18（3）：37⁃40.ZHU Rupeng，PAN Shengcai.Study of Prediction of Fretting⁃fatigue Life under High⁃Low Cycle Complex Loading ［J］.JournalofMechanical Strength，1996，18（3）：37⁃40.

［12］ 古远兴，温卫东，崔海涛.高低周载荷作用下燕尾榫结构的微动疲劳寿命预测［J］.推进技术，2008（2）：240⁃243.GU Yuanxing，WEN Weidong，CUI Haitao.Predic⁃tion of Fretting Fatigue Life of Dovetail Joint un⁃der High⁃cycle and Low⁃cycle Load［J］.Journal of Propulsion Technology，2008（2）：240⁃243.

［13］ PARIS P C，GOMEZ M P，ANDERSON W E.A Rational Analytic Theory of Fatigue［J］.The Trend in Engineering，1961，13（1）：9⁃14.

［14］ TANAKA K.Fatigue Crack Propagation from a Crack Inclined to the Cyclic Tensile Axis［J］.Engi⁃neering Fracture Mechanics，1974，6（3）：493⁃507.

［15］ EI HADDAD M H，TOPPER T H，SMITH K N.Prediction of Non Propagating Cracks［J］.Engi⁃neering Fracture Mechanics，1979，11（3）：573⁃584.

［16］ NEWMAN J C，PHILLIPS E P，SWAIN M H.Fa⁃tigue⁃life Prediction Methodology Using Small⁃crack Theory［J］.International Journal of Fatigue，1999，21（2）：109⁃119.

［17］ NEWMAN J C，BROT A，MATIAS C.Crack⁃growth Calculations in 7075⁃T7351 Aluminum Al⁃loy under Various Load Spectra Using an Improved Crack⁃closure Model［J］.Engineering Fracture Me⁃chanics，2004，71（16）：2347⁃2363.

［18］ PUGNO N，CIAVARELLA M，CORNETTI P，et al.A Generalized Paris’Law for Fatigue Crack Growth［J］.Journal of the Mechanics and Physics of Solids，2006，54（7）：1333⁃1349.

［19］ 殷之平，黄其青.SN-Paris全寿命综合模型［J］.西北工业大学学报，2007，25（3）：327⁃330.YIN Zhiping，HUANG Qiqing.SN⁃Paris Total⁃life Comprehensive Model［J］.Journal of Northwestern Polytechnical University，2007，25（3）：327⁃330.

［20］ 倪向贵，李新亮，王秀喜.疲劳裂纹扩展规律Paris公式的一般修正及应用［J］.压力容器，2006，23（12）：8⁃15.NI Xianggui，LI Xinliang，WANG Xiuxi.General Modification and Application of the Paris Law for Fatigue Crack Propagation［J］.Pressure Vessel Technology，2006，23（12）：8⁃15.

［21］ 李舜酩.机械疲劳与可靠性设计［M］.北京：科学出版社，2006:35⁃139.LI Shunming.Mechanical Fatigue and Reliability Design［M］.Beijing：Science Press，2006：35⁃139.

［22］ ELBER W.The Significance of Fatigue Crack Clo⁃sure［M］//Damage Tolerance in Aircraft Struc⁃tures.Toronto：ASTM International，1971：230 ⁃242.

［23］ QIAN J，FATEMI A.Fatigue Crack Growth under Mixed⁃mode I and Ⅱ Loading［J］.Fatigue&Frac⁃ture of Engineering Materials&Structures，2010，19（10）:1277⁃1284.

［24］ 中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.GB4161⁃1984金属材料平面应变断裂韧性KIC试验方法［S］.北京：中国标准出版社，2008.General Administration of Quality Supervision，In⁃spection and Quarantine of the People’s Republic of China，Standardization Administration of the People’s Republic of China.GB4161⁃84 Standard Test Method for Plane⁃strain Fracture Toughness of Metallic Materials［S］.Beijing：Standards Press of China，2008.

［25］ 赵少汴，王忠保.抗疲劳设计——方法与数据［M］.北京：机械工业出版社，1997：473⁃477.ZHAO Shaobian，WANG Zhongbao.Anti Fatigue Design—Method and Data［M］.Beijing：Engineer⁃ing Fracture Mechanics，1997：473⁃477.

［26］ 中国航空研究院.应力强度因子手册（增订版）［M］.北京：科学出版社，1993：352⁃356.Chinese Aeronautics Research Instute.Handbook of Stress Intensity Factors（Revised Edition）［M］.Bei⁃jing：Science Press，1993：352⁃356.*