基于Kriging插值的失谐叶盘气动 结构耦合振动特性分析

杨文军 张锴锋 王 磊 袁惠群

1.沈阳航空航天大学机电工程学院，沈阳，110136

2.沈阳航空航天大学航空制造工艺数字化国防重点学科实验室，沈阳，110136

3.东北大学机械工程与自动化学院，沈阳，110819

0 引言

压气机是航空发动机的关键组成部分，实际生产过程中由于制造误差、材质不均、使用中磨损不均或为抑制颤振的主观设计等因素，使得叶盘系统各扇区间会存在一定的失谐量。失谐导致的耦合振动和振动局部化现象较严重地影响了叶盘系统的稳定运行，并且越来越多地受到工程技术人员的重视。WEI等［1］研究了叶盘系统的振动模态局部化问题，解释了失谐引起振动模态局部化的现象。PIERRE等［2］研究了失谐叶盘系统气弹耦合下的振动模态局部化问题。结合传递矩阵法和摄动法，OTTARSSON等［3］研究了具有随机失谐因素时叶盘结构系统自由振动的局部化问题。YOO等［4］建立了失谐叶盘类结构的简化模型，研究了振动局部化现象。王红建等［5］建立了失谐叶盘系统振动的质量-弹簧模型，并提出了自动选择模态法用于该类问题的求解。王建军等［6］利用3种模态局部化因子，进行了典型叶盘结构失谐振动模态局部化程度的定量确定。基于ANSYS软件，张钊等［7］模拟了失谐叶盘的振动响应局部化特性，数值仿真结果与试验结果吻合较好。邵帅等［8］利用有限元法和子结构模态综合法，分析了失谐叶盘结构振动特性和模态局部化特性。综上所述，人们在失谐叶盘模型中往往把气动力简化为等效载荷，并作用于叶片上。由于简化存在误差，这样处理不能考虑气体流场对叶片的真实作用情况，而建立气动-结构耦合的失谐叶片-轮盘系统具有重要的工程意义。目前，失谐叶盘系统的气动-结构耦合动力学问题仍有待进一步研究。

气动-结构耦合动力学研究的关键在于流体-固体交界面数据传递问题。近年来，多种流体-结构耦合问题中的数据交换算法得到了发展。GOURA等［9］提出了一种常体积转换（CVT）方法，该方法是一种与结构模态无关的局部插值方法。STEIN 等［10］和 DWIGHT［11］将流体网格模型假设为一个符合线弹性方程的弹性固体，并且采用一种特殊的技术来保持边界层和高梯度区域的网格质量。曾强［12］采用三维线性插值方法对ANSYS和FLUENT中的网格数据进行变换，并对不同材料和转速的叶片模型进行流固耦合计算。仲继泽等［13］使用快速动网格技术计算结构及流场网格节点位移，并更新流场网格，实现流场与结构振动的空间同步求解。但如何使载荷数据传递的精度更高、更新后的流场网格质量更好，还有待深入研究。

本文以某型航空发动机压气机转子为研究对象，考虑叶排间动静干涉的影响，对压气机叶盘转子内部的三维流场进行模拟。通过静频试验引入叶片失谐量，基于Kriging模型完成耦合界面载荷数据的传递，分析压气机转子叶片表面非定常气动载荷的分布规律，并讨论失谐和气动载荷对压气机转子叶盘系统振动特性的影响。

1 计算模型及理论

1.1 数值模型的建立

本文的物理模型分为结构和流场两部分，结构区域以某型压气机转子叶盘系统为研究对象。为考虑叶排间动静干涉的影响，流场区域选取压气机前一级静叶和下游动叶的三维流场通道，其中，静子叶片数为42，转子叶片数为38。应用商用CFD软件的专业前处理工具Gambit对流体域进行网格划分，生成结构化六面体网格，单元总数为884 044，节点总数为1 005 952。经检查网格的长宽比小于5，正交性大于10，延展比小于1 000，网格的质量良好。固体域在有限元软件ANSYS中进行前处理，叶片和轮盘分别采用Solid185单元和Solid187单元进行网格划分，得到网格的单元总数为358 348，节点总数为1 468 672，具体模型见图1。

图1 计算模型Fig.1 The model of computation

压气机动静叶流场的交界面采用滑移网格处理，选择RNG k-ε湍流模型和隐式耦合求解方法。压气机工作转速为11 383 r/min，进口总压为105Pa，温度为300 K，出口静压为108 kPa，固壁为无滑移绝热壁面，介质为可压缩理想空气。综合考虑动叶的旋转速度和非定常计算的耗时性，选定物理时间步长为T/60，即2.31 μs，其中，T为动静干涉周期，动静干涉频率f0=1/T。

对于叶盘系统，叶片材料为钛合金TA11，其密度为4 370 kg/m3，弹性模量E0=113 GPa，泊松比为0.3；轮盘材料为钛合金TC17，其密度为4 680 kg/m3，弹性模量为112 GPa，泊松比为0.3。固体域求解时，对毂筒侧节点自由度进行全约束。

为了使计算模型更加接近工程实际，需考虑叶盘系统的失谐差异性。本文采用叶片静频试验和有限元数值模拟相结合的方法预测真实结构响应的失谐差异性，实现失谐参数的识别。叶片的静频测试方案见图2。

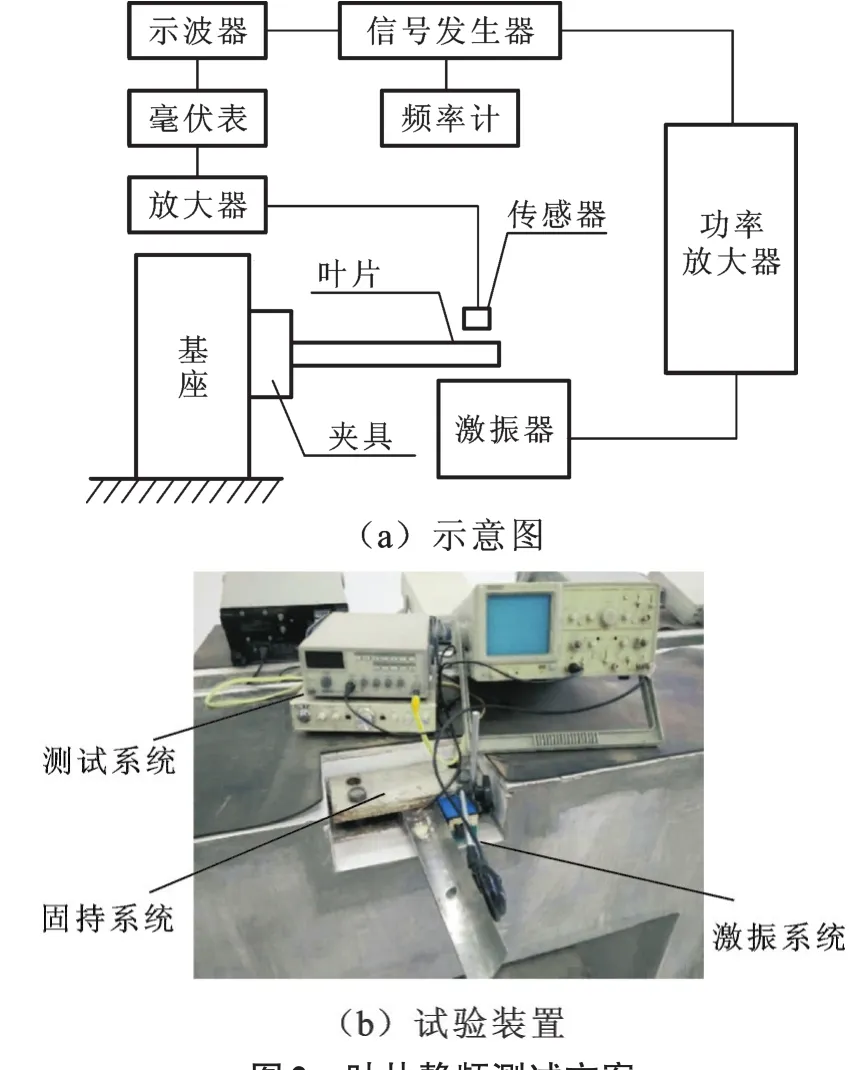
图2 叶片静频测试方案Fig.2 Testing project of blade natural frequencies

利用上述方法得到失谐弹性模量与叶片一阶静频之间，近似为线性关系。通过线性拟合可以得到失谐弹性模量随叶片一阶静频变化的线性表达式：

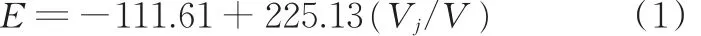
式中，E为失谐弹性模量，GPa；Vj为叶片j一阶弯曲静频测试值；V为谐调叶片（与材料弹性模量E0相对应）一阶弯曲静频测试值。

利用式（1），代入失谐叶片的一阶弯曲静频测试值，即可得到相对应的失谐弹性模量。

1.2 控制方程

1.2.1 结构动力方程

叶片结构动力学响应通常描述为

式中，M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；u为叶片结构位移；u̇为叶片结构速度；ü为叶片结构加速度；F为作用于叶片的气动载荷。

叶片的气动载荷可简化为简谐激励［14］。设

式中，umax为位移幅值；Fmax为气动载荷幅值；α为位移相位角；φ为气动载荷相位角；ω为振动频率。

将式（3）、式（4）代入式（2），整理得

通过求解式（5），可以得到叶片在气动载荷作用下的响应。边界条件可令耦合界面上流体壁面位移与固体壁面位移相等，通过流场计算获得。

1.2.2 流体动力方程

流体流动受物理守恒定律的支配，基本的守恒定律包括：质量守恒定律（continuity equa⁃tion）、动量守恒定律（Navier-Stokes equation）、能量守恒定律（energy equation）及组分质量守恒方程（species equation）。尽管以上方程的变量个数不同，但均反映了单位时间、单位体积内物理量的守恒性质。用ϕ表示通用变量，则控制方程的形式为

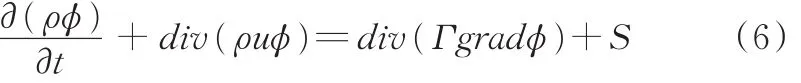
式中，为瞬态项；div(ρuϕ)为对流项；div(Γgradϕ)为扩散项；S为源项。

流体域满足质量守恒、动量守恒及能量守恒等物理守恒定律，边界条件为耦合面上流体壁面速度与固体壁面速度相等。由于压气机中流体属三维非稳态、带旋转的不规则运动，故须考虑湍流模型。本文选用标准k-ε模型，其湍流能与耗散率的控制方程为

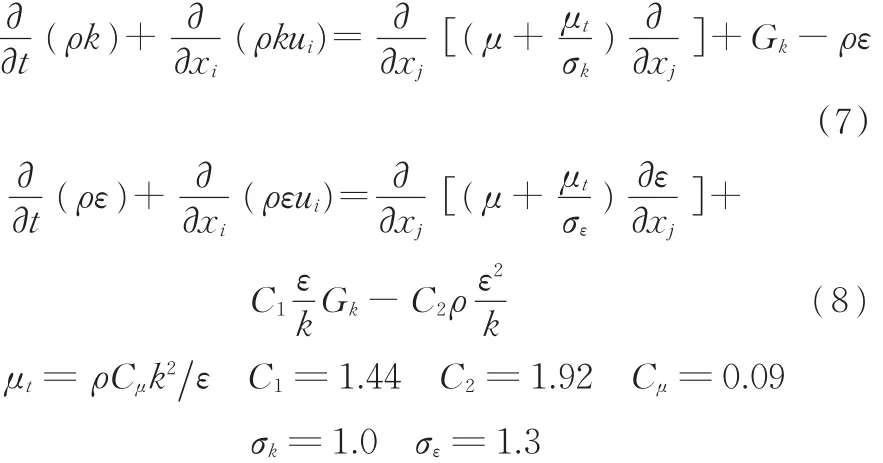
式中，ρ为气体密度；μ为流体的动力黏滞系数；k为湍流能；ε为湍流耗散率；μt为湍流黏度。

2 气动-结构耦合方法

2.1 气动-结构耦合分析流程

压气机叶盘系统的气动-结构耦合分析流程主要包括三大部分：压气机流场的三维模拟、基于Kriging插值的气动载荷传递和叶盘系统的气动-结构耦合分析，具体流程见图3。

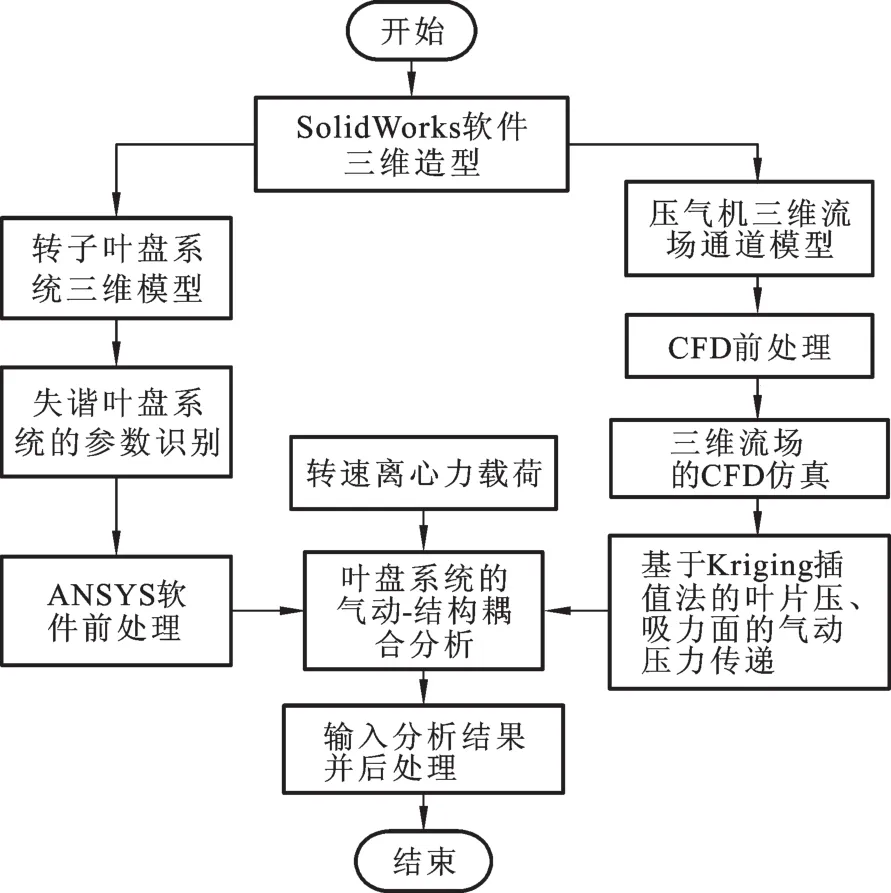
图3 压气机流固耦合分析流程Fig.3 Analysis process of compressor fluid-structure coupling dynamics

仿真分析流程如下：①基于Gambit软件建立压气机三维流场的CFD模型；②基于Fluent软件进行三维流场CFD仿真；③基于静频试验和数值模拟进行叶盘系统失谐参数识别；④基于ANSYS软件建立转子叶盘结构的有限元模型；⑤基于Kriging模型的叶片压力面、吸力面气动载荷的传递；⑥基于ANSYS软件的叶盘系统气动-结构耦合动力特性分析；⑦输出分析结果，并进行后处理。

2.2 耦合界面载荷传递方法

对于气动-结构耦合分析，耦合界面数据传递问题是解决流固耦合问题的关键。本文基于Kriging模型的耦合界面数据传递程序，实现了流场气动载荷向结构场的传递。

Kriging模型起源于地质统计学［15⁃16］，是一种估计方差最小的无偏估计模型，它可以较好地预估未知点处载荷值的分布情况。Kriging模型中的全部函数值与自变量之间的关系由多项式和随机分布表示：

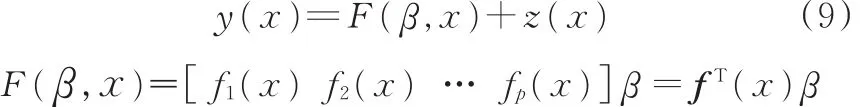
式中，F(β,x)为回归模型；z(x)是均值为0、方差为σ2的统计随机过程；x为空间自变量；β为基函数系数。

经推导获得插值计算未知点x处的预测值ŷ (x)：

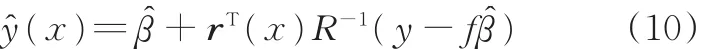
其中，r为观测点与样本点之间的相关性；R为任意两个样本点之间的相关函数；y为设计点的目测响应值；f为设计空间的一个全局模型，为多项式函数。上述参数可由已知点的载荷分布获得。

经过对压气机内部三维流场的模拟，获得了流场动叶表面的气动载荷。通过dacefit函数，根据耦合面流场节点坐标和气动压力来建立Kriging模型。采用predictor函数，根据Krig⁃ing模型计算结构场耦合面各节点的气动压力。基于优化算法对Kriging模型相关参数θk进行优化，来提高气动载荷的传递精度。采用上述方法进行气动载荷传递的程序编制。具体流程见图4。

根据Kriging模型实现了流固耦合界面气动载荷的传递，流场耦合面节点的气动压力及载荷数据传递后结构场耦合面节点的气动压力分布分别见图5、图6。

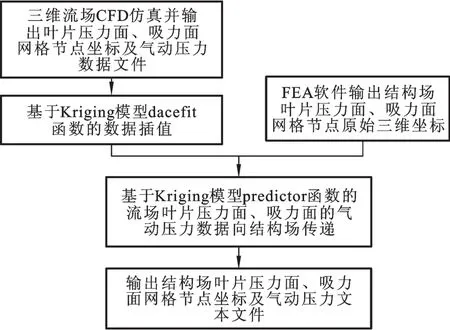
图4 气动载荷传递的程序流程图Fig.4 Program process of aerodynamic pressure transfer

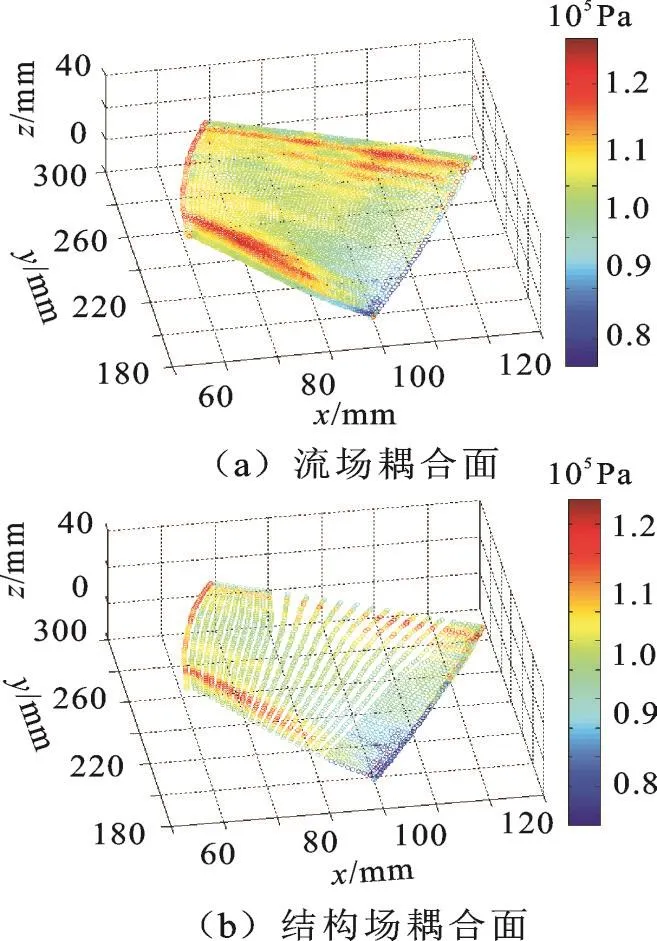
图5 叶片压力面节点气动压力分布图Fig.5 Node aerodynamic pressure on blade pressure surface

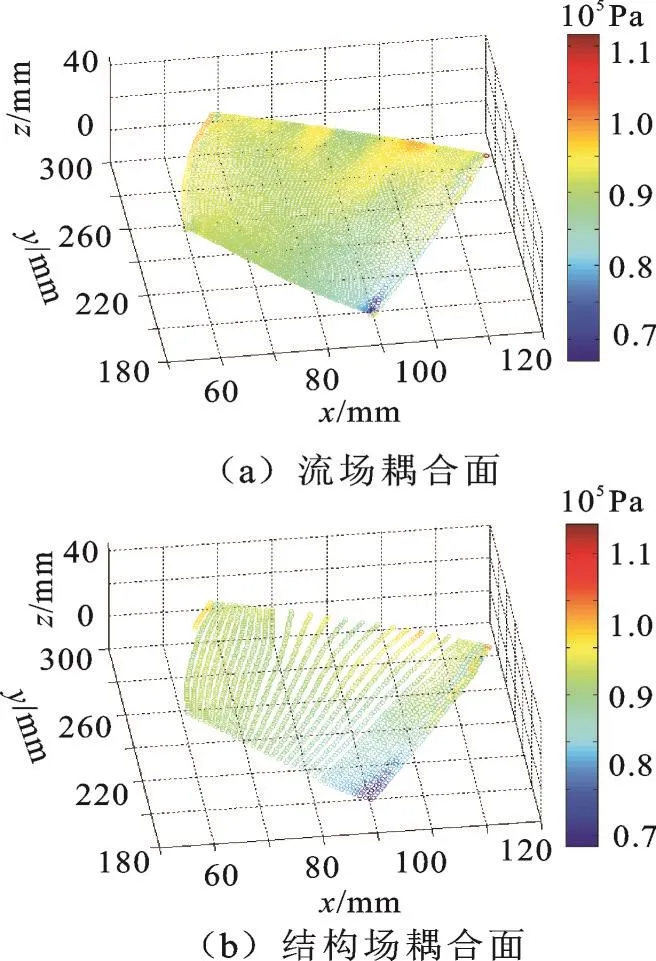
图6 叶片吸力面节点气动压力分布图Fig.6 Node aerodynamic pressure on blade suction surface

对比插值前后叶片表面气动压力的分布图可以发现，吸力面和压力面的结构节点气动压力分布与流场节点气动压力分布吻合良好，说明利用Kriging模型进行气动压力载荷的传递可以满足压气机叶盘系统气动-结构耦合力学的计算要求。

3 计算结果讨论与分析

3.1 转子叶片表面的非定常气动载荷分布

为了揭示转子叶片表面气动载荷的变化规律，在压气机三维流场模拟中对动叶压力面和吸力面的气动压力进行了监测，得到了动叶表面气动压力的变化曲线，见图7。

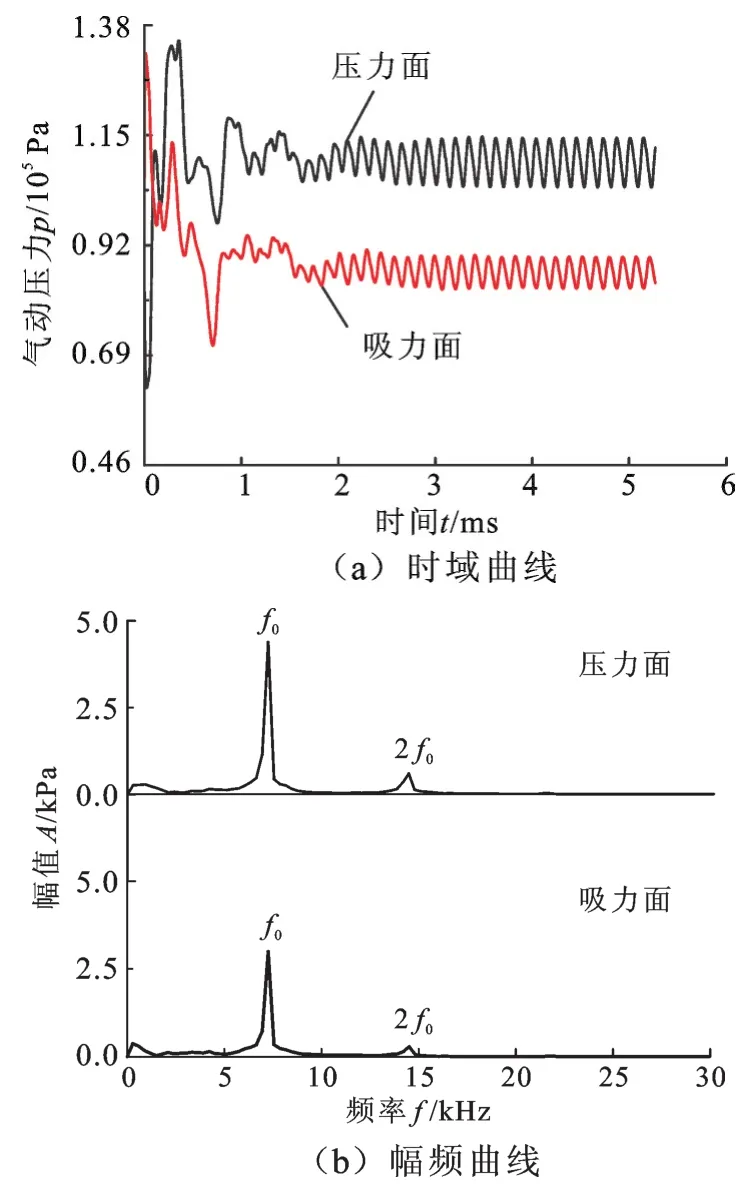
图7 动叶表面气动载荷的变化曲线Fig.7 Aerodynamic pressure curves of rotor blade surface

由图7中动叶表面气动压力的变化曲线可知，当压气机内部的流场收敛后，动叶压力面和吸力面的气动载荷也达到平稳。动叶压力面和吸力面气动压力的时域曲线见图7a，可以看出两时域曲线达到平稳后都处于振荡收敛状态，并呈现出正弦、余弦变化规律，且周期等于动静干涉周期T，可知压力面和吸力面所受到的气动载荷为非定常脉动压力。另外，压力面气动载荷的收敛值（109 kPa）远大于吸力面气动载荷的收敛值（86 kPa），而且压力面气动载荷的脉动幅值要明显大于吸力面的脉动幅值。动叶压力面和吸力面气动压力的幅频曲线见图7b，可以看出动叶表面的气动载荷主要受动静干涉的影响，压力面和吸力面气动载荷出现峰值的频率相同，皆为动静干涉的倍频，其中，一倍频（f0）分量占有主导地位，而二倍频（2f0）及更高倍频分量的峰值较小。同时，压力面气动载荷的频谱峰值要远大于吸力面的频谱峰值，可见压力面气动载荷的非定常性相比吸力面更强。

经过分析初步掌握了动叶表面压力的分布情况，为了更加详细地获得动叶表面气动载荷的分布细节，绘制了动叶压力面和吸力面在干涉周期T内气动压力的变化曲线和等值线图。

由图8可以看出，压力面的气动压力在5T/8时刻左右出现极小值，在T时刻附近取得极大值，而吸力面在T/2时刻左右出现极大值，在T时刻取得极小值。除了气动压力极值点出现的时刻稍有不同外，动叶压力面和吸力面的气动压力在干涉周期T内的变化规律呈相反趋势，具体见图9和图10。

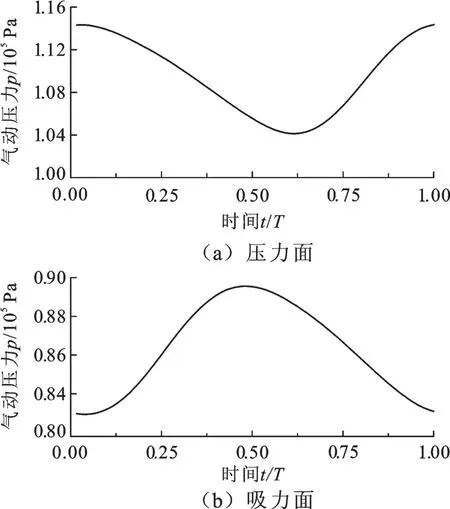
图8 干涉周期T内动叶表面气动压力的变化曲线Fig.8 Aerodynamic pressure curves of rotor blade surface at interaction period T

动叶压力面气动压力的等值线见图9，可以发现动叶压力面的气动压力从T/8至T/2时刻逐渐减小，5T/8时刻，压力面的气动压力取得极小值，随后压力面的气动压力值开始逐渐增大，在T时刻左右取得极大值，这与图8a中压力面气动压力变化曲线反映的规律一致。还注意到在干涉周期T内，叶片表面的压力涡存在周期性的迁移与耗散，动叶前缘激起的压力涡从压力面底部运动至顶部（①②③④位置），到达顶部后等值线梯度达到最大，气动压力取得极大值；之后压力涡又从前缘运动至尾缘（⑤⑥⑦⑧位置），最终脱离动叶压力面流向出口区域，等值线梯度趋于平缓，气动压力取得极小值，可见压力涡的变化过程与非定常气动压力的变化规律是相吻合的。

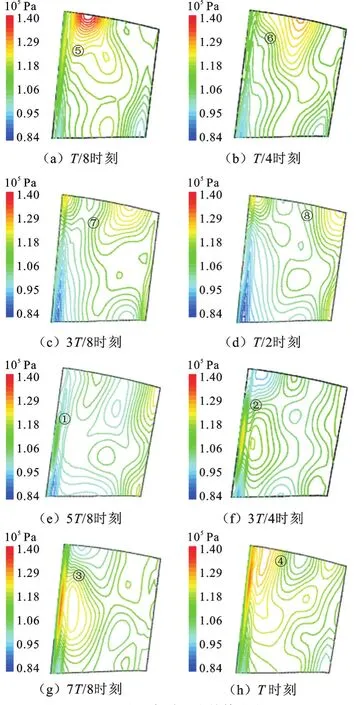
图9 压力面气动压力的等值线图Fig.9 Aerodynamic pressure contour maps of rotor blade pressure surface

动叶吸力面气动压力的等值线见图10，与压力面相比，动叶吸力面气动压力的变化有很大差异。从图10可以很清楚地看到，在吸力面前缘存在一条低压带，且它在整个干涉周期内一直存在，这是由于受到来流对吸力面前缘的冲击和动叶旋转拖拽效应的相互作用，吸力面前缘形成了明显的低压区。在吸力面的中后部位置气动压力梯度的变化比较明显，可以看到从T/8至T/2时刻，气动压力逐渐增大；T/2时刻吸力面的气动压力取得极大值，随后开始逐渐减小；到达T时刻附近取得极小值，这与图8b中吸力面气动压力的变化曲线反映的规律是一致的。另外，与压力面一样，吸力面也存在压力涡的迁移与耗散，但主要集中于吸力面的中后部区域，相比压力面的涡强度要弱很多。

图10 吸力面气动压力的等值线图Fig.10 Aerodynamic pressure contour maps of rotor blade suction surface

3.2 失谐和气动载荷对叶盘振动的影响

在忽略和考虑气动载荷作用的情况下，分别对谐调和失谐叶盘系统进行了分析计算，获得了谐调和失谐叶盘系统的变形、应力和应变能分布情况，并讨论了气动载荷和叶片失谐对叶盘系统振动的影响规律，见表1、表2。

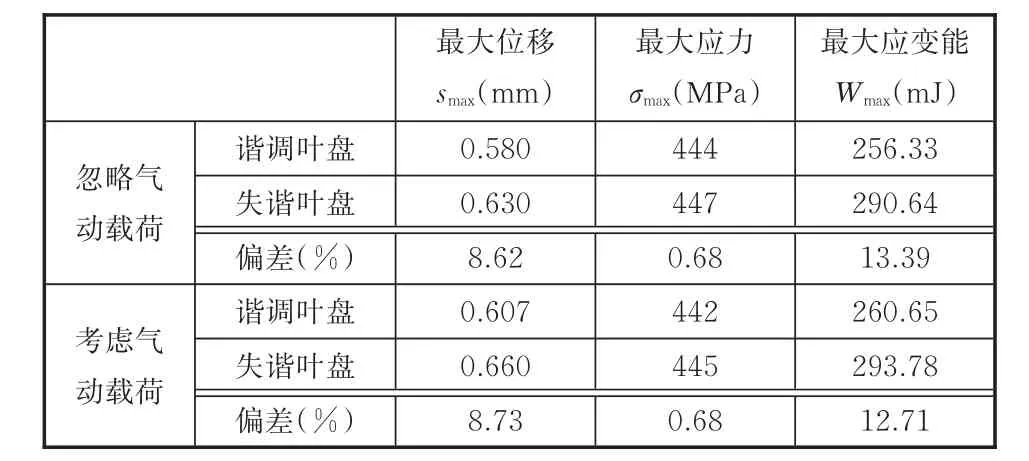
表1 失谐对叶盘系统振动的影响Tab.1 Mistuning effect on blade-disk system vibration

通过表1可以发现：在忽略和考虑气动载荷两种情况下，就最大位移和最大应变能而言，失谐叶盘系统要明显大于谐调叶盘，最大偏差分别为8.73%和13.39%；而最大应力变化不明显，两种叶盘偏差仅为0.68%。

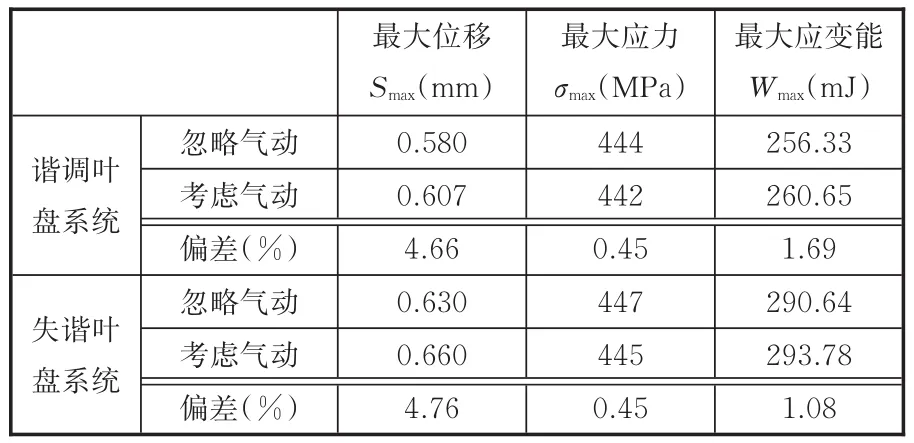
表2 气动载荷对叶盘系统振动的影响Tab.2 Aerodynamic load effect on blade-disk system vibration

通过表2可以发现：考虑气动载荷作用后，失谐和谐调叶盘系统的最大位移和最大应变能均出现了一定幅度的增大，最大增幅分别为4.76%和1.69%，而最大应力变化不明显。可见，气动载荷的作用使得叶盘系统的振动有所增强，这与失谐对叶盘系统振动的影响规律相似。叶盘系统各扇区的最大位移、最大Mises等效应力和应变能分布图见图11～图13。

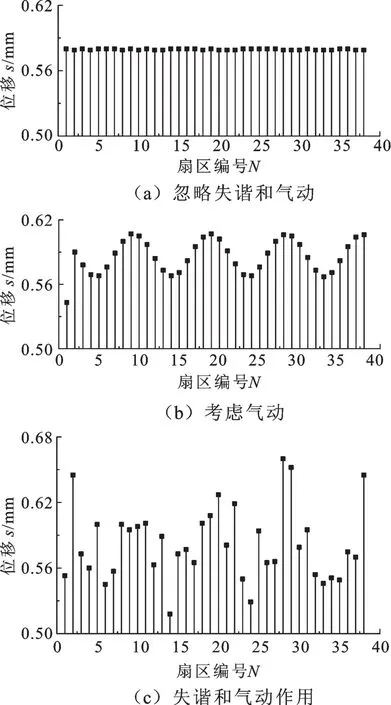
图11 叶盘系统各扇区的最大位移分布图Fig.11 Maximal displacement distribution of blade-disk sectors

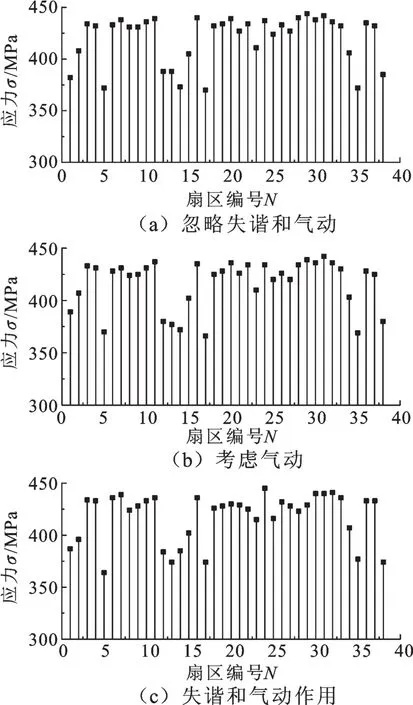
图12 叶盘系统各扇区的最大应力分布图Fig.12 Maximal stress distribution of blade-disk sectors

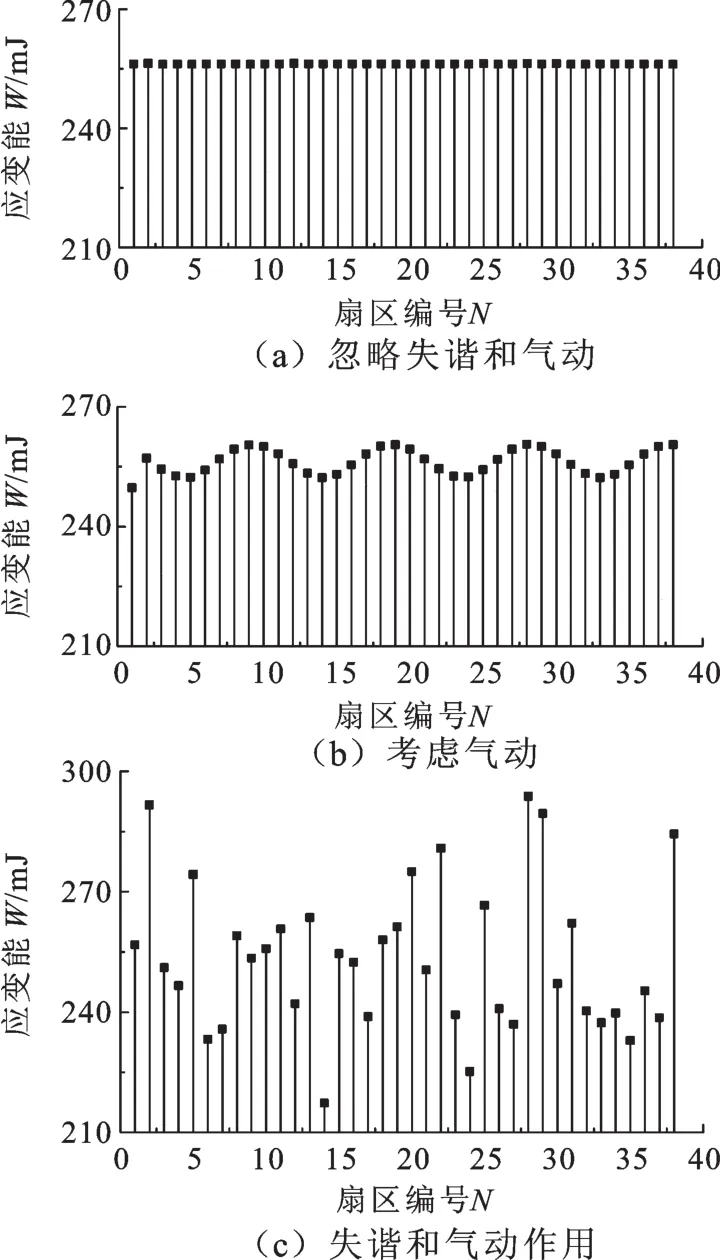
图13 叶盘系统各扇区的应变能分布图Fig.13 Maximal strain energy distribution of blade-disk sectors

由图11～图13可以看出，考虑失谐和气动载荷后，叶盘系统各扇区的最大位移和最大应变能的波动明显加剧，但最大应力变化较小，这说明失谐和气动载荷加剧了叶盘系统振动的不均匀性。为了进一步探讨失谐和气动载荷对叶盘系统叶片振动的影响规律，绘制了表3。

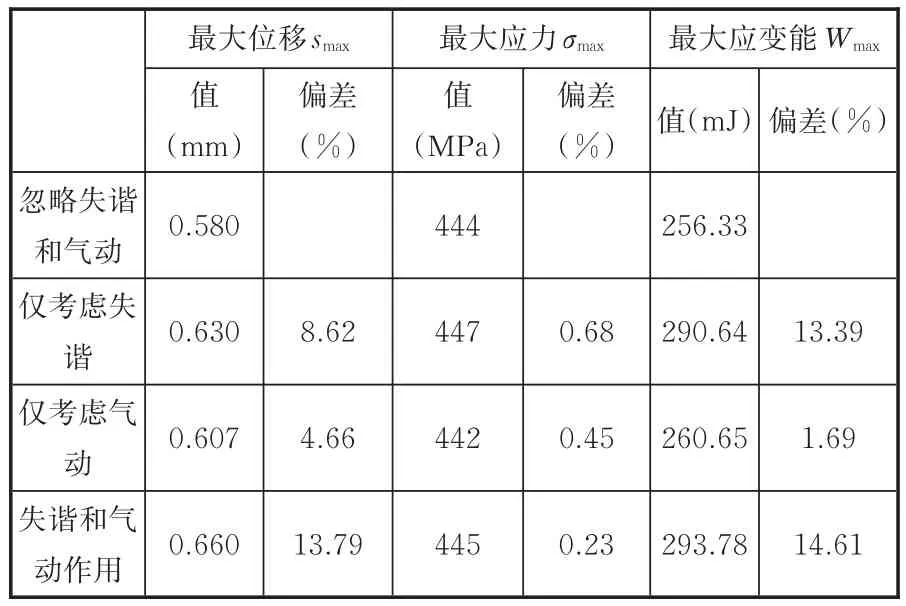
表3 失谐和气动载荷对叶盘系统振动的影响Tab.3 Mistuning and aerodynamic load effect on blade-disk system vibration

由表3可以发现：失谐和气动载荷对叶盘系统的最大位移和最大应变能影响比较明显，相对于忽略失谐和气动载荷情况的偏差分别为13.79%和14.61%，而对最大应力的影响较小。可见，叶片失谐导致了叶盘系统不均匀振动的出现。叶盘系统处于非定常的流场中，流体诱发的颤振破坏了叶盘结构的振动稳定性，故气动载荷进一步加剧了失谐叶盘系统的振动。

3.3 失谐叶盘系统的瞬态振动特性分析

为了进一步研究压气机叶盘系统的动力学特性，本文以流场仿真获得的各叶片的气动载荷作为外部激励，并考虑失谐因素和离心力的影响，求解了压气机叶盘系统的瞬态振动特性。提取气动载荷作用下失谐叶盘系统的位移云图和Mises应力云图（图14）。

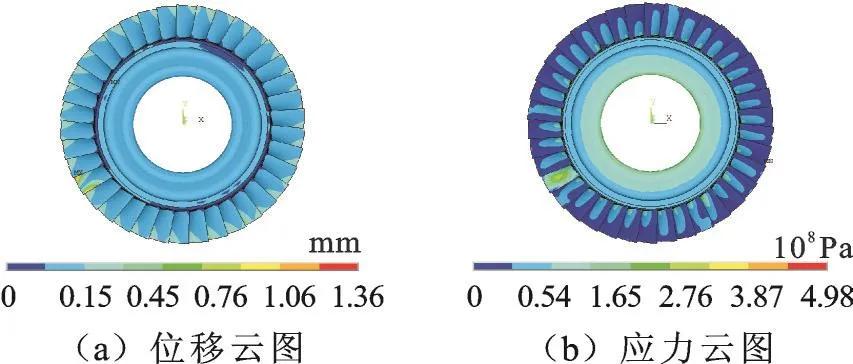
图14 气动载荷作用下失调叶盘的位移和应力分布图Fig.14 Displacement and stress distribution of mistuned blade-disk at effect of aerodynamic pressure

由图14可知，与谐调叶盘系统不同，失谐叶盘系统各叶片所在扇区的位移云图和应力云图存在明显的差异，这主要是由于失谐因素而导致叶片振动不均匀。经过计算，得到了失谐叶盘系统在气动载荷作用下位移和Mises应力的时域响应曲线，见图15。

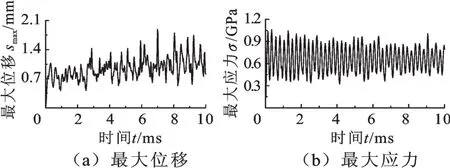
图15 气动载荷作用下失谐叶盘的时域响应曲线Fig.15 Time-domain response curves of mistuned bladedisk at the effect of aerodynamic pressure

由图15可以看出，时域响应曲线在一定幅值范围内进行波动，计算已经收敛。失谐叶盘系统的最大位移在2 mm以内，明显大于谐调叶盘系统的最大位移；最大Mises应力在1.1 GPa以内，与谐调叶盘系统的最大Mises应力基本一致。

针对计算获得的瞬态时域响应曲线进行频域分析，获得了气动载荷作用下失谐叶盘系统的频域响应曲线，见图16。由图16可以发现，气动载荷作用下叶盘系统的位移和Mises应力的波峰位置基本一致，最大峰值出现在7 200 Hz附近，这与叶片受到的非定常气动载荷频率f0是一致的，说明气动载荷作用下压气机叶盘系统的振动被激起。可见，气动载荷对失谐叶盘的振动，尤其是高频振动有着重要的影响。

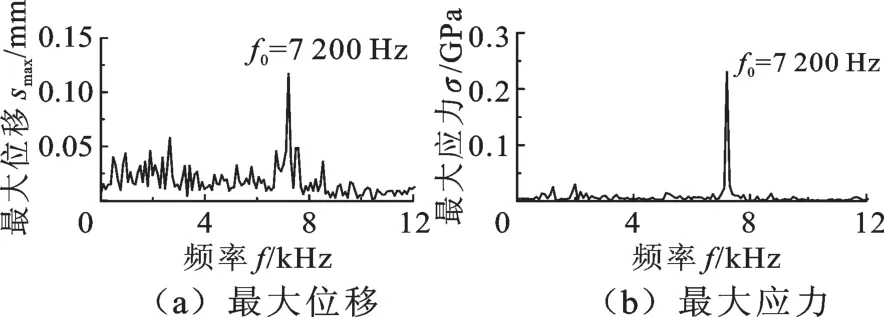
图16 气动载荷作用下失谐叶盘的频域响应曲线Fig.16 Frequency-domain response curves of mistuned blade-disk at the effect of aerodynamic pressure

4 结论

（1）基于Kriging模型插值后的压力面、吸力面结构节点的气动压力分布与流场节点的气动压力分布吻合较好，说明利用Kriging模型进行气动压力载荷的传递具有足够高的精度，可以满足压气机叶盘系统流固耦合力学的计算要求。

（2）压气机叶片受到的气动载荷为非定常脉动压力，且压力面和吸力面波动的主导频率皆为动静干涉频率f0的倍频，其中，一倍频（f0）分量占有主导地位。在干涉周期T内，动叶表面的压力涡存在周期性的迁移与耗散，压力面和吸力面气动载荷的变化规律呈相反趋势，就气动载荷的大小、脉动幅值和频谱峰值而言，压力面明显大于吸力面。

（3）忽略失谐和气动载荷情况下，叶盘系统各扇区叶片的最大位移和应变能的幅值变化平稳；而考虑失谐和气动载荷后，叶盘系统的最大位移和应变能有所增大，且发生了明显的波动。这说明失谐和气动载荷的作用加剧了叶盘系统的振动，增加了叶盘系统振动的不均匀性。

［1］ WEI S T，PIERRE C.Localization Phenomena in Mistuned Assemblies with Cyclic Symmetry Part I：Free Vibrations［J］.Journal of Vibration and Acous⁃tics，1988，110（4）：429⁃438.

［2］ PIERRE C，MURTHY D V.Aeroelastic Modal Characteristics of Mistuned Blade Assemblies⁃mode Localization and Loss of Eigenstructure［J］.AIAA Journal，1992，30（10）：2483⁃2496.

［3］ OTTARSSON G，PIERRE C.Vibration Localization in Mono⁃and Bi⁃Coupled Bladed Disks— a Transfer Matrix Approach［C］//34th Structures，Structural Dynamics，and Materials Conference.La Jolla，1993：3683⁃3697.

［4］ YOO H H，KIM J Y，INMAN D J.Vibration Local⁃ization of Simplified Mistuned Cyclic Structures Un⁃dertaking External Harmonic Force［J］.Journal of Sound and Vibration，2003，261（5）：859⁃870.

［5］ 王红建，贺尔铭，余仕侠.自适应摄动法在失谐叶盘受迫振动分析中的应用［J］.应用力学学报，2007，24（1）：107⁃110.WANG Hongjian，HE Erming，YU Shixia.Automat⁃ic Mode⁃selecting Method for Analysis to Forced Re⁃sponse of Mistuned Bladed Disks［J］.Chinese Jour⁃nal of Applied Mechanics，2007，24（1）：107⁃110.

［6］ 王建军，于长波，姚建尧，等.失谐叶盘振动模态局部化定量描述方法［J］.推进技术，2009，30（4）：457⁃461.WANG Jianjun，YU Changbo，YAO Jianyao，et al.Vibratory Mode Localization Factors of Mistuned Bladed Disk Assemblies［J］.Journal of Propulsion Technology，2009，30（4）：457⁃461.

［7］ 张钊，贺尔铭，赵志彬，等.基于耦合场压电分析的失谐叶盘振动仿真模拟［J］.航空计算技术，2011，41（5）：30⁃33.ZHANG Zhao，HE Erming，ZHAO Zhibin，et al.Ex⁃periment Numerical Simulation of Mistuning Bladed Disk Based on Piezoelectricity Coupling Field［J］.Aeronautical Computing Technique，2011，41（5）：30⁃33.

［8］ 邵帅，周柏卓，王相平.失谐叶盘结构振动模态局部化研究［J］.航空发动机，2014，40（3）：56⁃59.SHAO Shuai，ZHOU Baizhuo，WANG Xiangping.Investigation of Vibration Mode Localization of Mis⁃tuned Bladed⁃disk Assemblies［J］.Aeroengine，2014，40（3）：56⁃59.

［9］ GOURA G S L，BADCOCK K J，WOODGATE M A，et al.A Data Exchange Method for Fluid⁃struc⁃ture Interaction Problems［J］.Aeronautical Journal，2001，105（1046）：215⁃221.

［10］ STEIN K，TEZDUYAR T，BENNEY R.Mesh Moving Techniques for Fluid⁃structure Interactions with Large Displacements［J］.Journal of Applied Mechanics，2003，70（1）：58⁃63.

［11］ DWIGHT R P.Robust Mesh Deformation Using the Linear Elasticity Equations［C］//Computation⁃al Fluid Dynamics 2006.Belgium，2009：401⁃406.

［12］ 曾强.压气机转子叶片流固耦合计算及软件集成研究［D］.南京：南京航空航天大学，2006.ZENG Qiang.Research on Fluid⁃structure Coupling Calculation of Compressor Rotor Blade and Soft⁃ware Integration［D］.Nanjing：Nanjing University of Aeronautics and Astronautics，2006.

［13］ 仲继泽，徐自力.采用快速动网格技术的时空同步流固耦合算法［J］.振动工程学报，2017，30（1）：41⁃48.ZHONG Jize，XU Zili.Time⁃space Synchronizing Fluid Structure Coupling Method Using a Fast Dy⁃namic Mesh Technique［J］.Journal of Vibration En⁃gineering，2017，30（1）：41⁃48.

［14］ ADAMCZYK J J.Aerodynamic Analysis of Multi⁃stage Turbomachinery Flows in Support of Aerody⁃namic Design［J］.Journal of Turbomachinery，1999，122（2）：189⁃217.

［15］ 尹大伟，李本威，王永华，等.基于Kriging方法的航空发动机压气机特性元建模［J］.航空学报，2011，32（1）：99⁃106.YIN Dawei，LI Benwei，WANG Yonghua ，et al.Aeroengine Compressor Characteristics Metamod⁃eling Using Kriging Method［J］.Acta Aeronautica Et Astronautica Sinica，2011，32（1）：99⁃106.

［16］ 陈志英，任远，白广忱，等.粒子群优化的Kriging近似模型及其在可靠性分析中的应用［J］.航空动力学报，2011，26（7）：1522⁃1530.CHEN Zhiying，REN Yuan，BAI Guangchen ，et al.Particle Swarm Optimized Kriging Approximate Model and Its Application to Reliability Analysis［J］.Journal of Aerospace Power，2011，26（7）：1522⁃1530.*