基于粒子群优化算法的磁流变阻尼器多项式动力学建模方法

董致臻 冯志敏 伍广彬 刘小锋

1.宁波大学海运学院，宁波，315211 2.哈尔滨工业大学机器人技术与系统国家重点实验室，哈尔滨，150001

0 引言

磁流变液作为一种智能材料在无外加磁场时黏度很低，保持Newton流体特性；而在磁场作用下，磁性颗粒在载液中迅速形成链状结构，使磁流变液具有一定的屈服强度，呈现Bingham流体特性。磁流变阻尼器（magnetorheological damper，MRD）利用这一特性在工程领域得到广泛应用［1⁃3］。

建立精确的MRD动力学模型是实现复杂结构控制的关键。针对MRD动力学建模问题，国内外学者已做了大量研究，主要根据参数是否具有物理意义分为参数模型和非参数模型［4］。在参数模型中SPENCER等［5］提出Bonc⁃Wen模型，能较好地反映MRD滞回特性；KWOK等［6］基于粒子群优化（particle swarm optimization，PSO）算法提出的MRD双曲正切模型比Bonc⁃Wen模型所含参数少，易于推广应用。在非参数模型中，CHANG等［7］提出神经网络模型，建模方便且模型精度高；GAVIN等［8］最早在电流变阻尼器中应用Cheby⁃shev多项式模型，模型参数无需算法辨识且容易建模，模型精度取决于插值节点对应的数据误差；CHOI等［9］运用最小二乘法辨识传统多项式模型，并将其用于MRD动力学建模中，该方法存在高阶Runge振荡问题。近年来，为提高MRD多项式动力学模型精度和消除Runge振荡，周铁明等［10］提出将模型分成多个低阶多项式分别拟合再拼接的分段建模思想；孔祥东等［11］采用将低阶多项式模型与Bingham力学模型相结合的建模方法，提高了模型的整体拟合精度。但上述模型仍存在非线性参数多、计算冗长或模型分段处精度不足和Runge振荡现象，因此本文提出一种基于PSO算法［12］并应用Lagrange插值理论［13］的MRD动力学建模方法。

1 MRD性能试验

1.1 MRD试验平台

为研究MRD动力学特性，试验选用SG⁃MRD60型两级线圈套筒式磁流变阻尼器［14］。阻尼力检测在中机试验装备股份有限公司生产的SDS⁃100型动静试验机上进行，由液压动力源为伺服系统提供动力，以德国DOLI公司的EDC580控制器作为控制系统，并用Agilent E3632A电流源控制输出电流。试验平台和工作原理见图1。

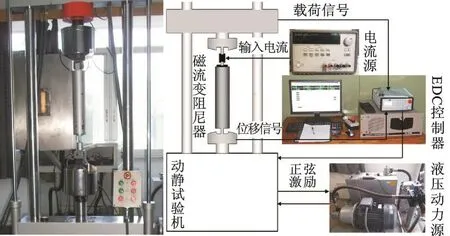
图1 试验平台和工作原理Fig.1 Test platform and working principle

1.2 试验方法

为探究不同外部激励与控制电流下的MRD动力学特性，通过EDC控制器在动静试验机输出不同频率、振幅的正弦激励信号，对应电流源输出给阻尼器的不同电流，分别进行阻尼器动力学性能试验。由于桥梁拉索振动频率主要在0.25～2.0 Hz之间，振幅由风雨激励和MRD安装位置决定［15］，故选取正弦激励（频率 1Hz、振幅15 mm），输入电流为0、0.25 A、…、1.5 A的试验工况。试验机采集载荷（阻尼力）信号，作为模型辨识依据。

2 模型参数识别

2.1 传统多项式模型

建立MRD传统多项式动力学模型［9］需根据活塞运动方向，把阻尼器动力学特性曲线分为一个正向运动曲线与一个反向运动曲线叠加。其中，输出阻尼力

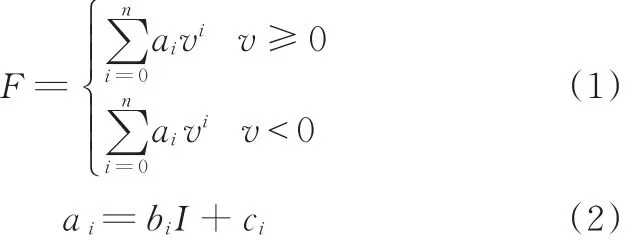
式中，ai为多项式系数；v为活塞瞬时速度；n为多项式阶数；I为电流；bi、ci为电流相关系数，可根据F、v、I试验值辨识得到。

根据活塞运动方向，将v≥0定义为正向运动，v＜0定义为反向运动。

2.2 Chebyshev多项式模型

建立Chebyshev多项式模型［8］需要先确定多项式阶数，再计算Chebyshev插值节点，最后将插值点试验数据代入Lagrange插值公式。建立n阶插值多项式模型需要n+1个插值节点，区间［a，b］上的Chebyshev插值节点［13］:

其中，n为多项式阶数，区间[a,b]为对应工况下MRD的活塞速度变化范围，可由下式计算得到：

式中，A为激振振幅；f为激振频率；φ0为初始活塞相位；t为当前时刻。

n阶Lagrange插值多项式由n+1个n阶插值函数构成，插值函数

构成的n阶Lagrange插值多项式为

式中，yi为插值点对应的函数值。

2.3 模型辨识对比及分析

由于篇幅所限，仅选用6阶、12阶多项式进行分析。根据试验工况数据，分别对上述2种模型进行参数辨识并作对比分析。其中,多项式模型用MATLAB最小二乘法工具箱作参数辨识，得到6阶多项式模型参数辨识结果（表1），绘制的速度⁃阻尼力曲线见图2、图3。

表1 6阶多项式模型参数识别结果Tab.1 The results of parameter identifications of the 6th order polynomial model

由于Chebyshev插值节点需根据活塞速度变化范围确定，将工况点试验参数代入式（4），得到活塞速度变化范围为±94.25 mm/s。再将式（3）求得的Chebyshev插值点对应的试验数据代入Lagrange插值多项式，并经MATLAB Simplify函数对多项式化简。最终6阶Chebyshev多项式模型插值节点与对应多项式系数见表2、表3。

表2 6阶Chebyshev多项式模型参数结果Tab.2 The parameter results of the 6th order Chebyshev polynomial model

图2 6阶多项式模型及试验曲线Fig.2 The 6th onder polynomial models and test curves

由图2、图3可知，高阶传统多项式模型与试验测量的输出阻尼力差值变化很大，并且曲线在两个端点处发生剧烈Runge振荡，试验中发现Runge现象在模型提高到8阶时出现，而高阶Chebyshev多项式模型避免了端点处Runge振荡。12阶Che⁃byshev多项式模型拟合效果明显优于6阶Cheby⁃shev多项式模型，说明Chebyshev多项式模型精度随多项式阶数增加而提高，建模时需兼顾运算速度选择较高的多项式阶数。此外，随MRD输入电流的减小，速度⁃阻尼力曲线平顺度变差，尤其在无电流工况，Chebyshev多项式模型曲线过渡段图像严重失真，出现局部凸变现象。

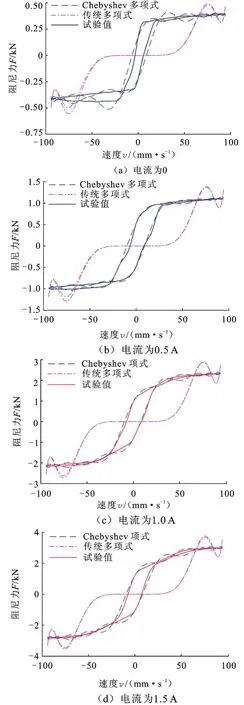
图3 12阶多项式模型及试验曲线Fig.3 The 12th order polynomial models and test curves

3 动力学优化建模

为优化动力学建模方法，提出利用PSO算法优化插值节点，并结合插值节点对应试验数据，将其代入Lagrange插值方程，经MATLAB Simplify函数化简得到所需的多项式模型。

表3 6阶Chebyshev多项式模型插值节点Tab.3 The interpolation nodes of the 6th order Chebyshev polynomial model

3.1 PSO算法的插值节点求解

3.1.1 PSO算法原理

PSO算法［12］中每个粒子可以看作是解空间中的一个点，假定粒子的群体规模为m，粒子的维数为d，全部粒子的速度及位置：

式中，i为粒子索引，i=1，2，…，m；k为当前迭代次数；v(k)id为第i个粒子在第k次迭代飞行速度矢量的第d维分量的速度；x(k)id为是第i个粒子在第k次迭代飞行速度矢量的第d维分量的位置；p(k)id为第i个粒子的个体最优解的第d维分量；p(k)gd为群体最优解的第d维分量；c1、c2为学习因子；r1、r2为（0，1）的随机数。

上述变量中，所有粒子的位置范围都包含在所选试验工况之内，每个粒子x的d维位置变量是多项式模型中d个插值节点在MRD动力学试验数据中的索引值，构建n阶多项式所需的粒子维度d=n+1。PSO算法优化结束后，最优插值节点的索引值保存在全局历史最优位置pg中。

适应度函数为PSO算法的优化目标函数，在插值节点求解时，适应度函数反映了多项式计算模型输出值与实际试验值之间的偏差。优化通常以最小化适应度函数值为目标，表达式为

式中，f（x）为适应度函数；Fj为第j个阻尼力试验值；Ln(xi)为xi粒子插值确定的多项式模型；vi为第j个活塞速度试验值，dat为建模数据量。

3.1.2 算法优化流程

对PSO算法进行改进，首先加入排序算法，将所有粒子（插值向量）内各插值节点的索引值按由小到大的顺序排列，消除不同索引顺序的最优解更新后对其余粒子优化方向的干扰，通过保持所有粒子位置的有序性来缩短算法收敛时间；然后将全局适应度计算放在个体适应度计算之后进行，以减少运算时间。

采用PSO算法进行插值节点优化，优化过程见图4。主要步骤如下：

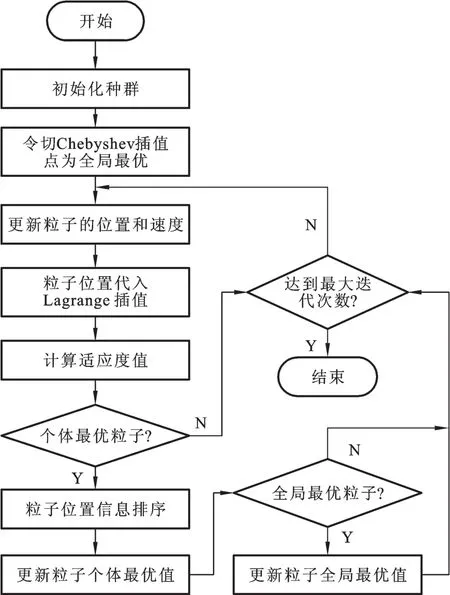
图4 插值节点优化流程图Fig.4 Interpolation node optimization flow chart

（1）初始化种群，即随机生成粒子位置、速度信息,然后将各粒子位置信息代入式（9）计算，得到初始个体最优值。

（2）将式（8）更新后的各粒子位置信息代入式（6），得到Lagrange插值多项式，并计算式（9）适应度值。

（3）若粒子当前适应度值优于个体最优值，则将该粒子排序并更新个体最优值，否则进入下一轮循环；若个体最优的粒子同时达到全局最优，则更新全局最优值，否则直接进入下一轮循环。

（4）重复步骤（2）～（3），达到最大迭代次数后程序结束。

将优化后插值节点对应试验数据代入La⁃grange插值多项式，得到Lagrange插值多项式模型。经MATLAB Simplify函数化简，得到优化后的多项式动力学模型。

3.2 求解结果与比较分析

为体现PSO算法在高阶多项式建模方法中的作用，选取12阶PSO算法优化多项式模型与Che⁃byshev多项式模型，分别在正弦激励（频率1 Hz、振幅15 mm），输入电流0、0.25 A、…、1.5 A工况下进行建模研究。PSO算法参数设置见表4。

表4 PSO算法参数Tab.4 PSO algorithm parameters

根据传统多项式模型，按活塞运动方向将试验数据分为正、反2组，并分别结合Lagrange插值多项式，用PSO算法优化插值节点。优化结果代入Lagrange插值公式，形成Lagrange插值多项式，经MATLAB化简，所得多项式动力学模型速度-阻尼力曲线见图5，适应度收敛轨迹见图6。利用MATLAB最小二乘法工具箱结合输入电流工况，根据式（2）对多项式模型系数进行辨识，得到模型参数（表5）。

图5 2种多项式模型及试验曲线Fig.5 Two polynomial models and test curves

图6 适应度收敛轨迹Fig.6 Fitness convergence trajectory

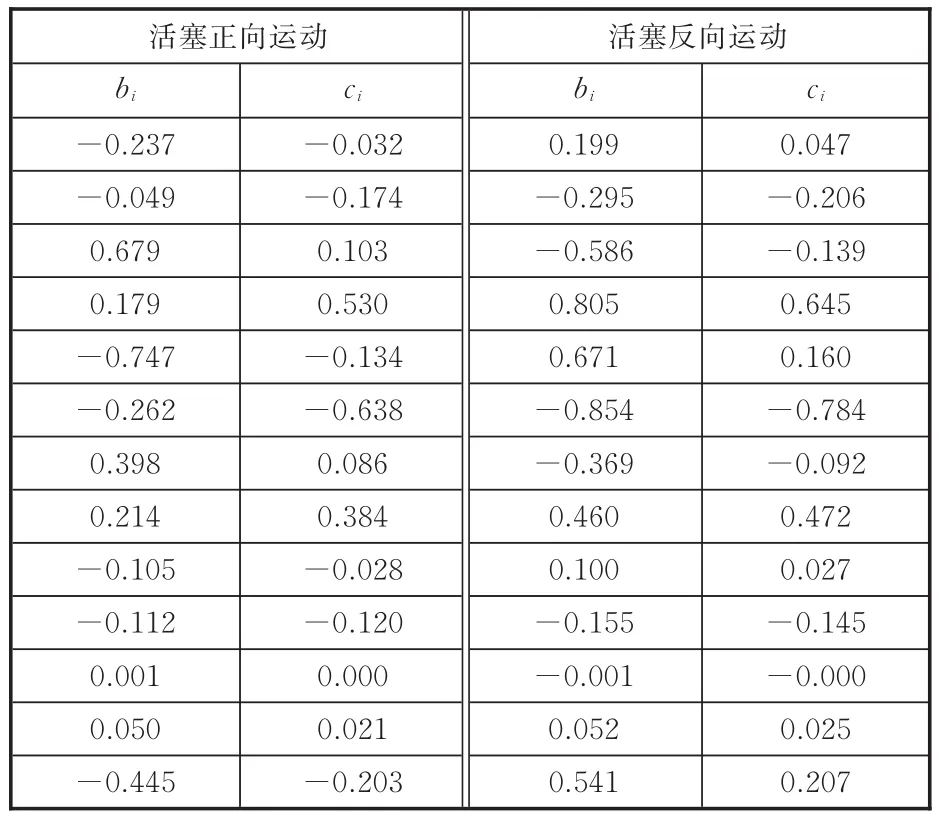
表5 12阶PSO优化多项式模型参数Tab.5 Parameters of the 12th order PSO optimal polynomial model

为进一步评价该建模方法的有效性，根据模型平均累计相对误差公式：

式中，FP(vi)为动力学模型在速度点vi的阻尼力值；F(vi)为阻尼力在vi速度点的实测值。

对上述试验结果进行比较。计算结果见表6。

表6 模型相对误差对比Tab.6 Comparison of model relative error %

由图5可知，经PSO算法优化插值节点建立的12阶多项式模型不仅消除了Runge振荡，而且拟合精度优于Chebyshev多项式模型。由于Che⁃byshev插值建模方法中插值节点无法根据实测阻尼力调整，因此，在输入电流0～1.5 A工况下，PSO算法建模方法的相对累计误差均小于Che⁃byshev多项式模型（表6），平均相对误差下降47.0%。图5反映出PSO算法具备良好的收敛性，能有效满足实际工程应用需求。

4 结论

在MRD动力学特性试验基础上，对传统多项式模型与Chebyshev模型进行了模型辨识及对比分析，提出基于PSO算法的多项式动力学优化建模方法，得出如下结论：

（1）传统多项式建模方法简便，但会出现6阶精度不足、12阶Runge振荡失真问题。Chebyshev多项式模型虽然消除了高阶Runge振荡，并且模型精度随多项式阶数增加而提高，但在低电流工况下，图像曲线过渡段模型仍然呈现凸变失真现象。

（2）由于Chebyshev多项式模型建模精度受插值点试验数据精度的影响，并且插值节点的选取只与MRD活塞速度变化范围有关，无法根据实测阻尼力调整，因此PSO算法建模方法能够有效提高MRD多项式动力学模型精度。试验表明，在正弦激励频率1 Hz、振幅15 mm、电流0～1.5 A工况下，相比Chebyshev多项式模型，PSO算法多项式模型平均相对累计误差下降47.0%，能较真实地反映MRD的动力学特性。PSO算法收敛性好，具有良好的工程应用前景。

［1］ VULCU C，DUBINĂ D，POPA N，et al.Hybrid SeismicProtection System：Buckling Restrained Brace of Nano⁃Micro Composite Magneto Rheologi⁃cal Damper［J］.Ce/papers，2017，1（2/3）：2936⁃2945.

［2］ 胡红生，肖平，江明，等.基于鱼群算法的永磁体⁃电磁阀式磁流变阻尼器半主动悬架系统［J］.中国机械工程，2017，28（21）：2526⁃2533.HU Hongsheng，XIAO Ping，JIANG Ming，et al.Experimentally Reducing Vibration and Noise of Gear System Using Magneto⁃rheological Damper［J］.China Mechanical Engineering，2017，28（21）：2526⁃2533.

［3］ WANG Zhihao，CHEN Zhengqing，GAO Hui，et al.Development of a Self⁃powered Magnetorheological Damper System for Cable Vibration Control［J］.Ap⁃plied Sciences，2018，8（1）：118.

［4］ JIANG Z，CHRISTENSON R E.A Fully Dynamic Magneto ⁃rheological Fluid Damper Model［J］.Smart Materials&Structures，2012，21（6）：65002⁃65013.

［5］ SPENCER B F Jr，DYKE S J，SAIN M K，et al.Phenomenological Model for a Magnetorheological Damper ［J］.Journal of Engineering Mechanics，1997，123（3）：230⁃238.

［6］ KWOK N M，HA Q P，NGUYEN T H，et al.A Nov⁃el Hysteretic Model for Magnetorheological Fluid Dampers and Parameter Identification Using Particle Swarm Optimization［J］.Sensors and Actuators A，2006，132：441⁃451.

［7］ CHANG C，ROSCHK P E.Neural Network Model⁃ing of a Magnetorheological Damper［J］.Journal of Intelligent Material Systems&Structures，1998，9（9）：351⁃358.

［8］ GAVIN H P，HANSON R D，FILISKO F E.Elec⁃trorhelogical Dampers，Part 2：Testing and Modeling［J］.Applied Mechanics，1996，63（3）：676⁃682.

［9］ CHOI S B，LEE S K，PARK Y P.A Hysteresis Model for the Field⁃dependent Damping Force of a Magnetorheological Damper［J］.Journal of Sound and Vibration，2001，245（2）：375⁃383.

［10］ 周铁明，陈恩伟，陆益民，等.磁流变液阻尼器的改进多项式模型及验证［J］.振动与冲击，2014，33（7）：221⁃226.ZHOU Tieming，CHEN Enwei，LU Yimin，et al.Modified Polynomial Model and Its Verification for a MR Damper［J］.Journal of Vibration and Shock，2014，33（7）：221⁃226.

［11］ 孔祥东，李斌，权凌霄，等.磁流变液阻尼器Bingham⁃多项式力学模型研究［J］.机械工程学报，2017，53（14）：179⁃186.KONG Xiangdong，LI Bin，QUAN Lingxiao，et al.Study on Dynamic Bingham⁃polynomial Model of a MRF Damper［J］.Journal of Mechanical Engineer⁃ing，2017，53（14）：179⁃186.

［12］ KENNEDY J，EBERHART R.Particle Swarm Op⁃timization［C］//Proceedings of IEEE International Conference on Neural Networks.Perth，1995：1942⁃1948.

［13］ 李庆扬，王能超，易大义.数值分析［M］.5版.北京：清华大学出版社，2008：23⁃25.LI Qingyang，WANG Nengchao，YI Dayi.Numeri⁃cal Analysis［M］.5th ed.Beijing：Tsinghua Univer⁃sity Press，2008：23⁃25.

［14］ 李宏伟，冷志鹏，徐慧.一种新型磁流变阻尼器：中国，CN201110378234.6［P］.［2012⁃04⁃25］.LI Hongwei，LENG Zhipeng，XU Hui.A Novel Mag⁃netorheological Damper：China，CN201110378234.6［P］.［2012⁃04⁃25］.

［15］ 冯志敏，张兴军，张刚，等.斜拉索⁃阻尼器系统建模与减振控制研究［J］.农业机械学报，2013，44（增1）：282⁃287.FENG Zhimin，ZHANG Xingjun，ZHANG Gang，et al.System Modeling and Vibration Reduction Control for Stayed Cable⁃Magnetorheological Dam⁃per［J］.Transactions of the Chinese Society for Ag⁃ricultural Machinery，2013，44（s1）：282⁃287.*