神光-Ⅲ精密光学模块侧装机械手运动学分析

宋代平 袁岳军 郭宗环 王 康

1.重庆大学机械传动国家重点实验室，重庆，400044 2.重庆东风小康汽车有限公司，重庆，405321

0 引言

惯性约束聚变（inertia confinement eusion，ICF）是激光束产生高能量聚变反应的一种方法。大型激光器装置（如美国的国家点火装置（Na⁃tional Ignition Facility，NIF）和中国的大型高功率激光装置）所需的大口径精密光学模块与相应机械件组合构成的在线可替换单元（line-replace⁃able unit，LRU）数目和种类繁多，规格不一，均为专门定制的易损、精密且价格昂贵的重要关键部件，能否保证绝对安全的携带并安装至主机试验装置内部，将直接影响到装置的工程建造与运行维护成本［1⁃3］。

六自由度是具有完整空间定位能力的机械手应具备的最小自由度，机械手若具有更多的自由度，将会显著改善其运动特性，增加机体灵活性和提高避障能力。然而自由度的增加会使机械手运动学分析变得更为复杂，尤其是机械手运动学逆解问题。文献［4］固定机械手的第三个关节，使其恒为0，从而把该机器人变为六自由度机器人，再引入臂形标志进行运动学逆解的求解。文献［5］采用位姿分离法，将7自由度串联机器人运动学逆解问题分解为位置逆解和姿态逆解两部分，并结合几何法和行程最短原则计算位置逆解和姿态逆解。文献［6］采用最短行程准则选取一组最接近于当前操作臂的解；文献［7］提出一种自寻优的方法来解决冗余机械臂关节限位的运动优化问题。

惯性约束聚变试验装置复杂、结构繁多，由此LRU转运装置必须准确定位和具备一定的避障能力。洁净精密光学模块是LRU中的一种，本文提出了一种用于洁净精密光学模块侧面装入神光-Ⅲ主机试验装置的八自由度侧装机器人，建立了运动学方程，并进行了运动学分析。

1 侧装机器人的结构组成

八自由度侧装机器人主要由立柱、升降台、摇臂关节（关节2～关节5)、调节机构和抓手等部件组成，见图1。

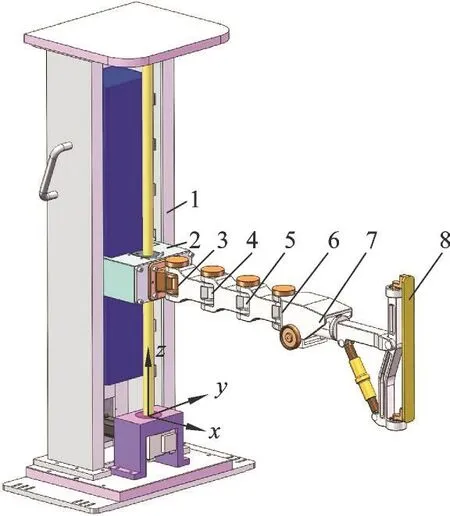
图1 八自由度侧装机器人结构Fig.1 Structure of 8-DOF side loading robot

侧装机器人的作业方式主要是垂直方向上的提升运动和水平面内的侧向运动。升降机构、侧送机构、摇臂关节决定了精密光学模块的位置，使模块能够沿x、y方向移动和绕z轴旋转一定角度；调节机构的作用是对模块的姿态进行微调，使模块能够绕x、y、z轴旋转一定角度，类似于人的手腕。八自由度串联侧装机器人机构简图见图2。

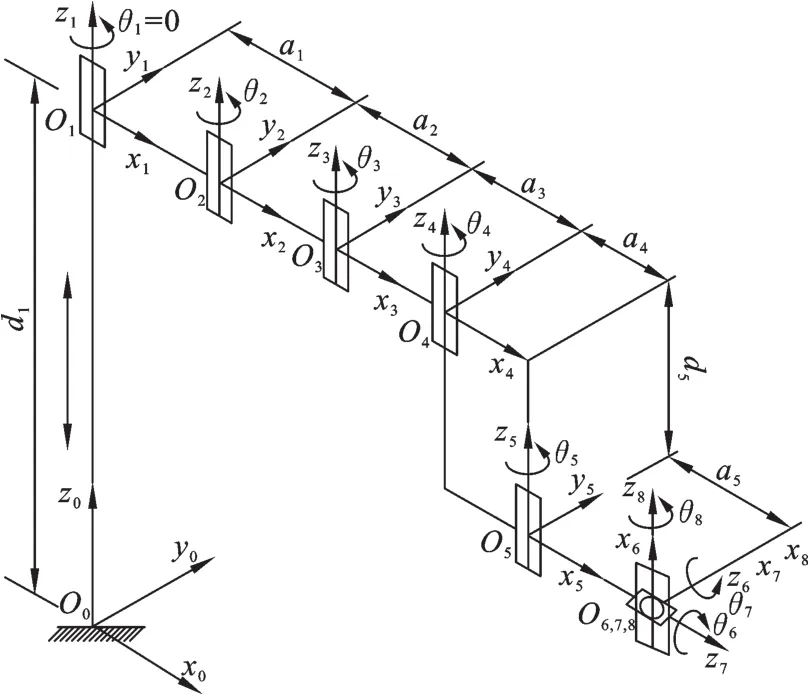
图2 八自由度侧装机器人机构简图Fig.2 Machine draft of 8-DOF side loading robot

2 运动学正解

机器人的运动学分析是性能分析和动力学分析的基础，对一个新型机构来说，运动学分析是机构分析的前提和基础，是进行机器人机构设计的首要任务。

机器人的正运动学问题是已知机器人各个关节的关节角，求末端执行器的位姿（位置和姿态）。侧装机器人采用D-H法（Denavit－Hartenberg ma⁃trix)［8⁃9］建立坐标系并推导机器人的运动学方程。侧装机器人D-H坐标系见图2，各连杆参数及关节变量见表1。

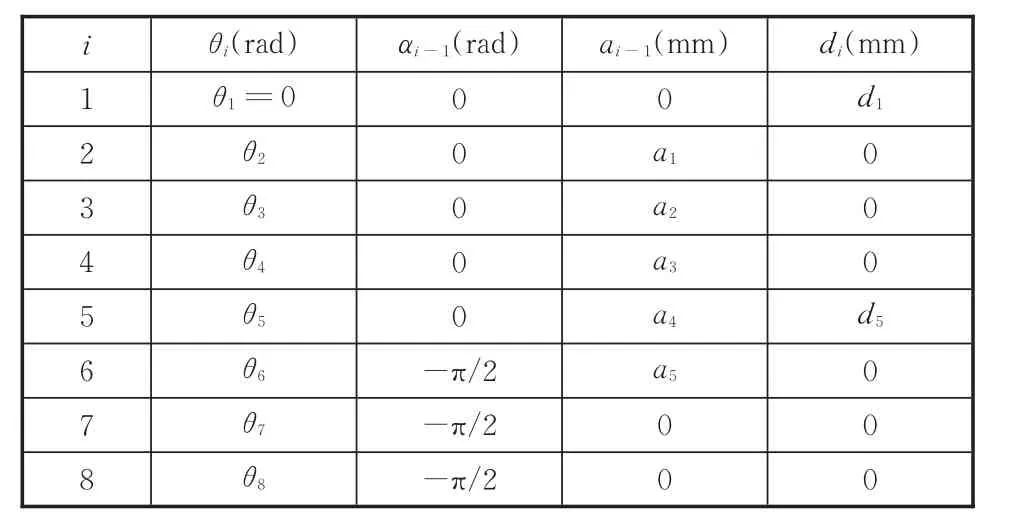
表1 连杆参数及关节变量Tab.1 Link parameters and joint variables

连杆变换矩阵

式中，c表示cos；s表示sin。

侧装机器人有8个自由度，据式（1）以及表1所示的连杆参数，可求得八自由度侧装机器人基座坐标系和末端执行器坐标系之间的总变换：

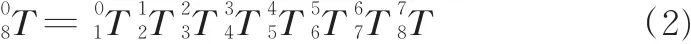
将右乘以得到工具端部和基座之间的总变换。为工具端部和末端连杆坐标系间的变换：

根据侧装机器人结构尺寸要求确定如下：a1=140 mm、a2=170 mm、a3=170 mm、a4=170 mm、a5=535 mm、d5=-10 mm。各变量范围如下：d1∈［200 mm，1 950 mm］；θ2，θ3，…，θ8∈［-π/2，π/2］。

各变量的初始值分别取d1=500 mm，θ2=0，θ3=0，θ4=π/2，θ5=0，θ6=π/2，θ7=π/2，θ8=0，代入式（3）可求得

由所得结果可知，与三维模型在同样状态下的测量值完全吻合（图3），表明D-H参数法求解结果是正确的。

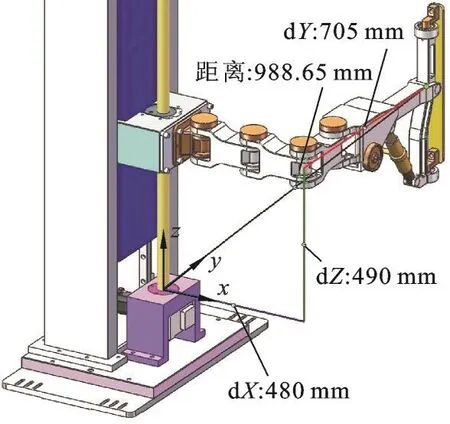
图3 运动学正解结果验证Fig.3 Kinematic positive solution verification

3 运动学逆解确定方法及实例验证

3.1 运动学逆解分析

机器人运动学逆解是在已知末端执行器位姿的情况下，求解各个关节变量。逆向运动学问题的求解相对复杂，可能存在多解也可能无解。PIEPER［10］证明了3个连续关节轴相交于一点的6R机器人逆运动学可解。DUFFY［11］证明了3个连续关节轴平行的6R机器人逆运动学可解，对于末端位姿确定的八自由度侧装机器人，逆运动学为已知末端执行器位姿08T，求解对应关节变量 d1、θ2、θ3、θ4、θ5、θ6、θ7、θ8的值，其求解过程非常复杂。由于一个末端位姿矩阵只有6个独立变量，故只能求解6个未知数。本文先采用关节变量虚化法，将关节2、3、4构造为虚拟关节，从而构建一个虚拟六自由度机器人，基于极限值均值法确定虚拟轴长a，采用解析法求解虚拟六自由度机器人的逆解。此外，采用占用空间最小法求解关节对八自由度机器人的逆解进行求解，具体求解步骤如下：

（1）设定关节2与关节5之间距离为a，构建虚拟关节，由此构建虚拟六自由度机器人（其中3个连续关节轴交于一点）；

（2）建立虚拟六自由度机器人逆运动学方程，根据极限值均值法原则求解a值；

（3）将末端位姿代入逆运动学方程并求解，得到d1、θ6、θ7、θ8；

（4）依据关节2、关节3和关节4的占用空间最小原则进行求解，得到θ2、θ3、θ4、θ5；

（5）考虑结构限制对所求逆解的各个变量进行取舍，最终得到一组待定解；

（6）将待定解代入正运动学方程进行验证；

（7）确认末端位姿。

建立虚拟六自由度机器人D-H坐标系，见图4，各连杆参数及关节变量见表2。

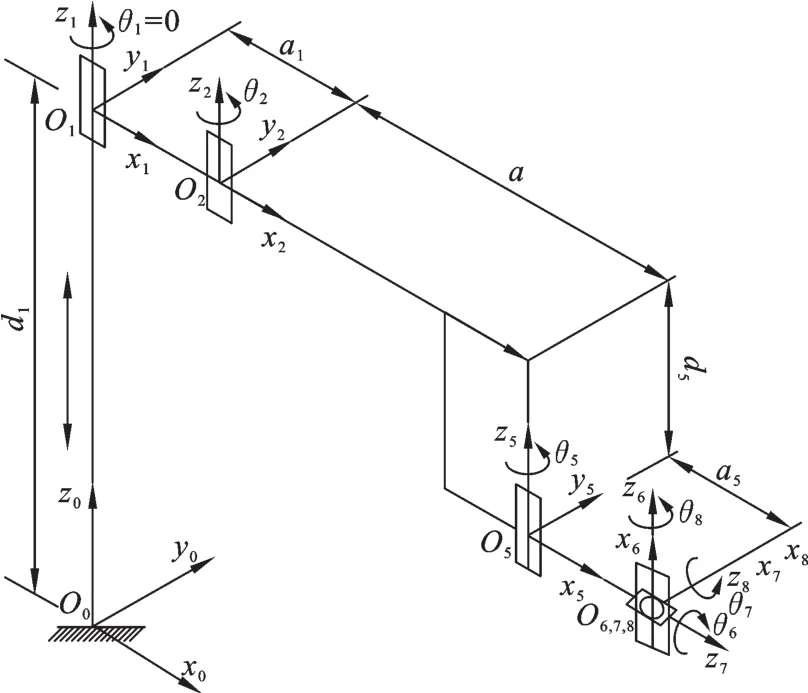
图4 虚拟六自由度机器人D-H坐标系Fig.4 Virtual 6-DOF robot D-H coordinate system

连杆变换矩阵i-1iT表示如下：

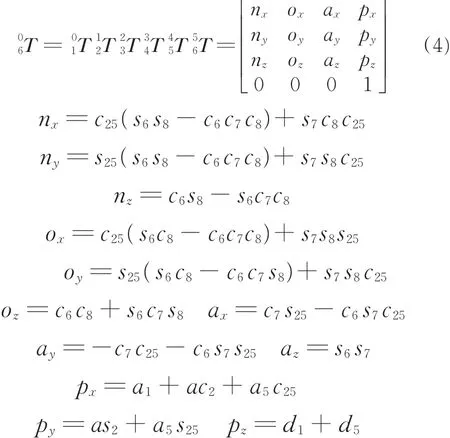
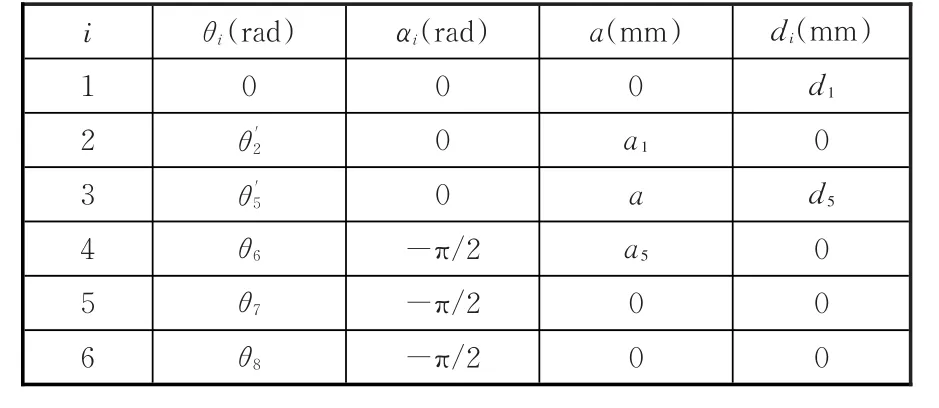
表2 连杆参数及关节变量Tab.2 Link parameters and joint variables

对于该虚拟六自由度机构，对应任何一种末端位姿，虚拟关节长度a都有无数种取值，为了求得该虚拟六自由度机构逆解，必须规定一种a值求解算法。如果a值是一个定值，则会很大程度缩小机器人的工作空间，因此本文采用极限值平均法确定虚拟关节长度a，其值与末端位姿相关，具体如下：

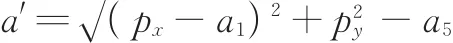
（2）当始终保证θ′5=π/2或-π/2时，a表达式如下：

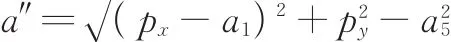
（3）为了保证处于比较合适的位置，a值取以上两种极限位置的平均值，即

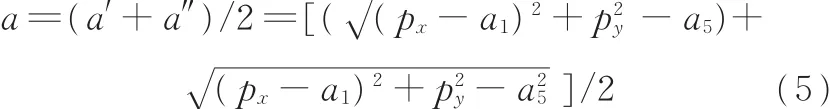
已知构建的虚拟六自由度机器人是按照Pieper准则设计的，因此可以得到封闭解。求解六自由度机器人运动学逆解的方法主要包括解析法和代数法［12⁃13］、几何法［14］、符号及数值方法［15］、神经网络法［16⁃17］等，本文采用矩阵逆乘的解析法求解运动学逆解。

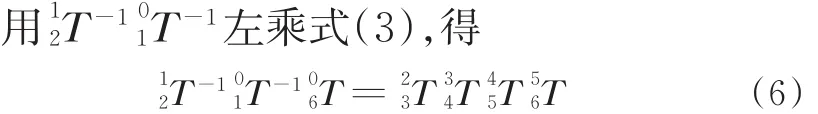
式（6）左边：

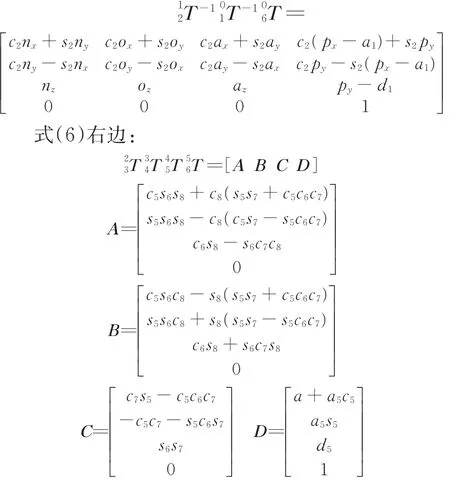
按解析法求得运动学逆解：

从上述解的表达式可以看到、分别最多可能有两个解，由于θ6、θ7、θ8和、相关，所以机器人最多可能有4组解。

3.2 侧装机器人逆解的确定

与通常采用最短行程准则和多移动小关节、少移动大关节的原则不同［18］，本文根据侧装机器人自身结构、作业环境和位置的特点，基于关节占用空间最小的思路来求取θ2、θ3、θ4、θ5的解。以关节2与关节5公垂线方向定为x轴，垂直于公垂线方向为y轴，建立平面直角坐标系（图5）。

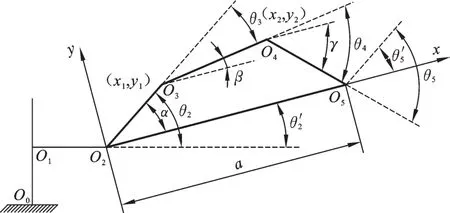
图5 关节的逆解坐标系Fig.5 Joint inverse coordinate system

设关节3、关节4的坐标分别为（x1，y1）、（x2，y2），根据“关节占用空间最小”的原则，需保证+最小，即求目标函数f=+的最小值，建立约束方程组：

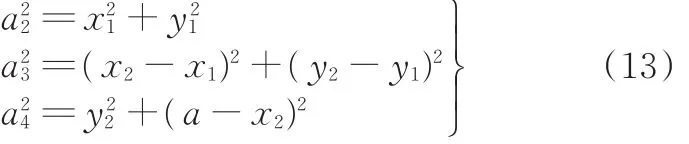
针对目标函数f的非线性，本文采用一种复杂的迭代算法——麦夸特算法［19］对其进行求解。最终目标函数的最优解在1stOpt（First Optimi⁃zation）中得到。根据已知的关节2、关节3坐标位置，得到关节角θ2、θ3、θ4、θ5如下：

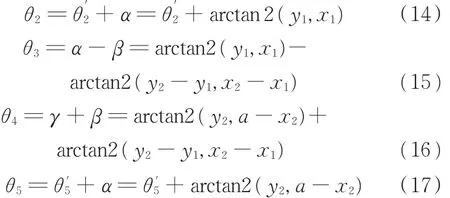
至此，八自由度侧装机器人的8个关节全部求出，运动学逆解已全部得到。

3.3 逆解实例验证

随机任意给定两个末端位姿如下：

根据给定的两种位姿，通过式（5）计算出两种位置下的a分别为409.509 0和435.224 8，将式（18）、式（19）代入式（7）～式（12）中得到虚拟六自由度的两组逆解（表3）。

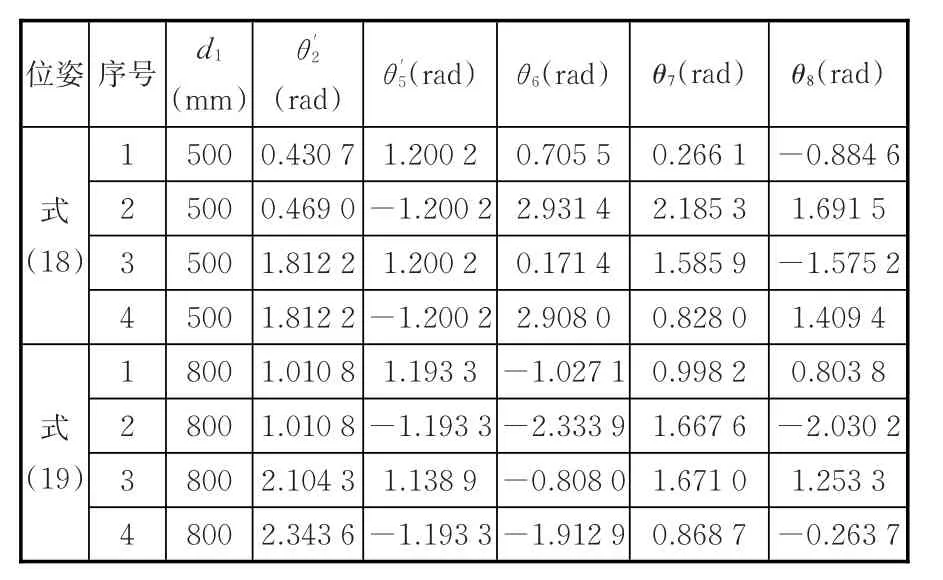
表3 式（18）和式（19）位姿下虚拟六自由度机器人逆解Tab.3 Inverse solutions of a virtual 6-DOF robot in poses of equation（18）and equation（19）

受侧装机器人自身结构约束，比较各关节转角范围，经正解验证，对应表3式（18）位姿下只有序号1的解满足要求，因此序号1的解就是待确定的解。式（19）位姿下序号1和序号4满足要求，但序号4的解中关节2超过允许转动范围，因此序号1是式（19）对应的待确定的解。

根据式（13），利用1stOpt软件优化后得到关节3和关节4的坐标值，将坐标值与表3中序号为1的解代入式（14）～式（17）中求得 θ2、θ3、θ4、θ5，即分别得到对应的八自由度侧装机器人的运动学逆解,如表4所示。

表4 式（18）和式（19）位姿下侧装机器人优化逆解Tab.4 Inverse solutions of side loading robots in poses of equation（18）and equation（19）

表4中的解是式（18）、式（19）位姿下逆解的优化解。将它们分别代入正运动学方程中可得

比较式（18）～式（21）可知：末端位置数据误差（Δpx，Δpy，Δpz）分别为（0.058 4，-0.031 7，0）mm和（0.043 3，0，0）mm，最大误差为0.012%，完全符合精度要求,从而确定了表4中的解是侧装机器人在式（18）、式（19）位姿下的逆解。分析表明，该方法确定求得的运动学逆解是正确可靠的,并且该方法能快速确定运动学逆解，从而为进一步研究机器人的轨迹规划及实时控制提供了理论基础。

4 结论

（1）本文以八自由度侧装机器人为研究对象，对其进行了运动学分析。根据侧装机器人的自身结构特点，采用D-H法建立连杆参数，推导得出了运动学正解方程。

（2）针对八自由度机器人逆运动学求解问题，采用关节变量虚化法构建出一个虚拟六自由度机器人。

（3）基于极限值平均法确定虚拟轴长，利用解析法得到虚拟六自由度机器人逆解。

（4）以关节占用空间最小为原则，结合麦夸特算法，利用1stOpt软件解算关节2、3、4位置，进而求解得到八自由度侧装机器人所有运动学逆解。

（5）通过实例验证逆解算法的正确性。运动学分析可以用于侧装机器人末端执行器的精确定位和运动规划，为实现八自由度侧装机器人的运动轨迹规划及实时控制等提供了理论基础。

［1］ 刘小波，谢志江，刘楠，等.一种光机洁净精密装校设备设计与研究［J］.中国机械工程，2010，21（2）：146⁃150.LIU Xiaobo，XIE Zhijiang，LIU Nan，et al.Design and Research of an Assembly Facility for Opticme⁃chanical Module for Cleaness and Precision［J］.Chi⁃na Mechanical Engineering，2010，21（2）：146⁃150.

［2］ 谢志江，李诚，刘楠，等.6自由度装校机器人逆解的确定［J］.吉林大学学报（工学版），2012，42（6）：1563⁃1568.XIE Zhijiang，LI Cheng，LIU Nan，et al.Determi⁃nation of Inverse Kinematics of a 6⁃DOF Installing⁃Calibrating Robot［J］.Journal of Jilin University（En⁃gineering and Technology Edition），2012，42（6）：1563⁃1568.

［3］ 谢志江，刘其南，袁晓东，等.大型高功率激光装置下装系统的碰撞检测［J］.重庆大学学报，2011，34（1）：21⁃25.XIE Zhijiang，LIU Qinan，YUAN Xiaodong，et al.Collision Detection for Down⁃load System in Large⁃scale SuperpowerLaserFacility［J］.Journalof Chongqing University，2011，34（1）：21⁃25.

［4］ 胡勇华，罗庆生，王娟，等.一种多用途8自由度机械手的运动学分析［J］.机械与电子，2006（7）：58⁃61.HU Yonghua，LUO Qingsheng，WANG Juan，et al.Kinematics Analysis of a Multi⁃purpose 8⁃DOF Ro⁃bot［J］.Machinery and Electronics，2006（7）：58⁃61.

［5］ 时凯飞，李瑞峰.7自由度仿人手臂运动学研究［J］.哈尔滨工业大学学报，2003（7）：806⁃808.SHI Kaifei，LI Ruifeng.Kinematics of Service Robot Bionics Arm［J］.Journal of Harbin Institute of Tech⁃nology，2003（7）：806⁃808.

［6］ 刘松国.6自由度串连机器人运动优化与轨迹跟踪控制研究［D］.杭州：浙江大学，2009.LIU Songguo.Research on Motion Planning and Trajectory Tracking Control of Six⁃DOF Serial Ro⁃bots［D］.Hangzhou：Zhejiang University，2009.

［7］ 田海波，马宏伟，魏娟.串联机器人机械臂工作空间与结构参数研究［J］.农业机械学报，2013，44（4）：196⁃201.TIAN Haibo，MA Hongwei，WEI Juan.Workspace and Structural Parameters Analysis for Manipulator of Serial Robot［J］.Transactions of the Chinese Soci⁃ety for Agricultural Machinery，2013，44（4）：196⁃201.

［8］ 王其军，杜建军.MOTOMAN机器人逆运动学新分析［J］.哈尔滨工业大学学报，2010，42（3）：451⁃454.WANG Qijun，DU Jianjun.A New Solution for In⁃verse Kinematics Problems of MOTOMAN Robot［J］.Journal of Harbin Institute of Technology，2010，42（ 3）：451⁃454.

［9］ 霍希建，刘伊威，姜力，等.具有关节限位的7R仿人机械臂逆运动学优化［J］.吉林大学学报（工学版），2016，46（1）：213⁃220.HUO Xijian，LIU Yiwei，JIANG Li，et al.Inverse Kinematic Optimization of 7R Humanoid Arm with Joint Limits［J］.Journal of Jilin University（Engineer⁃ing and Technology Edition），2016，46（1）：213⁃220.

［10］ PIEPER D L.The Kinematics of Manipulators un⁃der Computer Control［D］.California：Stanford University，1968.

［11］ DUFFY J.Analysis of Mechanisms and Robot Ma⁃nipulators［M］.London：Edward Arnold，1980：369⁃409.

［12］ PAUL R P，SHIMANO B E，MAYER G.Kinemat⁃ic Control Equations for Simple Manipulations［J］.IEEE Trans.SMC，1981，11（6）：449⁃455.

［13］ FU K S，GONZALEZ R C，LEE C S G.Robotics，Control，Sensins，Vision，and Intelligence［M］.New York：McGraw Hill，1987：78⁃82.

［14］ MANOCHA D，CANNY J F.Efficient Inverse Ki⁃nematics for General 6R Manipulators［J］.IEEE Transactions on Robotics and Automation，1994，10（5）：648⁃657.

［15］ KARLIK B，AYDIN S.An Improved Approach to the Solution of Inverse Kinematics Problems for Robot Manipulators［J］.Engineering Applications of Artificial Intelligence，2000（13）：159⁃164.

［16］ MAYROGA R V，SANONGBOON P.A Radial Basis Function Network Approach for Geometrical⁃ly Bounded Manipulator Inverse Kin ystem.Las Ve⁃gas，2003：3564⁃3569.

［17］ 陈学生，陈在礼，谢涛.基于神经网络的机器人操作手IKP精确求解［J］.机器人，2002，24（2）：130⁃133.CHEN Xuesheng，CHEN Zaili，XIE Tao.An Accu⁃rate Solution to the Inverse Kinematic Problem of a Robot Manipulator Based on the Neural Network［J］.Robot，2002，24（2）：130⁃133.

［18］ 熊有伦，丁汉，刘恩沧.机器人学［M］.北京：机械工业出版社，1993：54⁃60.XIONG Youlun，DING Han，LIU Encang.Robotics［M］.Beijing：China Machine Press，1993：54⁃60.

［19］ PAUL R P，ZHANG H.Computationally Efficient Kinematics for Manipulators with Spherical Wrists Based on the Homogeneous Transformation Repre⁃sentation［J］.The International Journal of Robotics Research，1986，5（2）：32⁃44.*