基于相关正交匹配追踪算法的风电机组滚动轴承稀疏故障诊断方法

李继猛 李 铭 王 慧 张金凤 张云刚

1.燕山大学电气工程学院，秦皇岛，066004 2.燕山大学里仁学院，秦皇岛，066004

0 引言

近几年，风能凭借着分布广泛、蕴藏量大等特点在世界各国得到了持续快速的发展［1］。2016年，我国风电开发建设总规模为3 083万kW，预计2050年我国风电装机容量将达到10亿kW，风电将成为发电主力［2］。滚动轴承作为风电装备的基础部件，一旦出现故障，将可能引发连锁反应，导致整个系统停机，造成巨大的经济损失和恶劣的社会影响。在故障发生的初期，嘈杂的外部环境以及电磁干扰等导致采集的信号含有较多噪声和干扰分量，信噪比较低，难以及时发现滚动轴承的故障征兆［3］，因此，选取正确的故障诊断方法对滚动轴承故障特征进行提取一直是风电装备故障诊断技术研究的热点和难点。

针对风电装备中滚动轴承振动信号的成分多样以及非平稳等导致故障特征难以提取的问题，稀疏分解理论提供了一种全新的思路。稀疏分解的概念由COIFMAN等［4］在1992年提出，其核心思想是利用不同的基函数构造超完备字典，将信号在字典上展开，得到最稀疏的表达方式。目前，稀疏分解中的重构算法主要有两类：一类是以基追踪（basis pursuit，BP）算法［5］为代表的凸松弛法；另一类是以匹配追踪（matching pursuit，MP）［6］和 正 交匹配追踪（orthogonal matching pursuit，OMP）［7］算法为代表的贪婪算法。由于OMP算法思想简单便于理解，不易陷入局部最优解，且收敛速度快，因而被广泛应用。基于这些重构算法的稀疏分解理论在故障诊断领域得到了广泛研究［8⁃9］。崔玲丽等［10］提出了并联基追踪算法，可以快速有效地进行故障信号分析，为机械故障信号提取提供了一种新思路；张晗等［11］将稀疏分解与形态成分分析相结合，用于航空发动机的轴承故障诊断，提高了故障特征提取精度。

为了尽可能准确地提取与故障成分相关的特征，受正交匹配追踪（OMP）算法启发，本文提出了相关正交匹配追踪（correlation orthogonal matching pursuit，COMP）算法用于实现滚动轴承故障特征的有效提取。

1 稀疏分解相关理论

1.1 稀疏分解

传统信号处理方法如傅里叶变换、短时傅里叶变换和小波变换等，其基函数可以看作是正交基，基函数一旦选定，则信号只能由此基函数展开成一系列加权和的形式，不具备自适应性，如用快速傅里叶变换处理变化较快的信号会出现吉布斯现象等。根据文献［4］的稀疏分解概念，基于信号特征选取合适的基函数作为原子，构造自适应超完备字典，通过计算信号与每一个原子的系数，来近似表达原信号。具体的数学模型为

式中，y为信号；D为构造的超完备字典；α为原子的系数；r为残差。

假设字典中有n个原子，原子用d表示，则该表达式可以进一步表示为

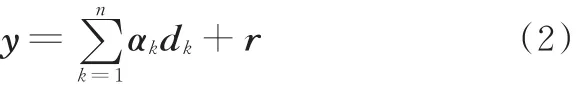
由式（2）可知，由于原子选择的随意性，一个信号在一个字典下可以有多种表达，而我们所需要的是最稀疏的表达，即所需原子越少越好，也就是αk中非零项最少。这同时又是一个基于l0范数的优化问题：

由式（3）可以看出，这是一个NP困难问题，未知量α由两个待确定的有效部分组成：解的支撑集和支撑集上的非零值。因此，一种聚焦于支撑集计算稀疏表示系数的算法被广泛应用于求解l0问题［12］，这类算法被称为贪婪算法。

1.2 正交匹配追踪

OMP算法是对MP算法的改进。由MP算法可知，在第k次迭代中有

式（4）中，r(k)与dk是正交的，即

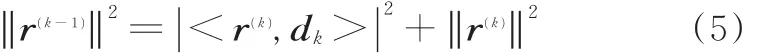
由于超完备字典的冗余性，在第k次迭代中，只能保证r(k)与dk正交，而无法保证r(k)与之前所选出的原子 dk-1，dk-2，…，d1都正交，这种非正交性会导致每次迭代的结果并不是最优而是次优，从而使得MP算法收敛需要很多次迭代。

OMP算法很好地解决了这个问题。由式（4）可以看出，MP算法在求解时，是将内积作为稀疏表示系数，而OMP在更新系数时，计算使得最小的α值。由矩阵相关知识可知，这种方式实际上求的是Dα=y的最小范数解，解得α=D+y，以此计算残差

由这种方式更新得到的残差rk与矩阵Dk（之前所选出的原子组成的矩阵）正交，这就保证了在之后的迭代中，不会再选择之前选择过的原子。

这种系数更新方式克服了MP算法容易陷入局部最优解的问题，大大加快了算法的收敛速度。但是OMP算法由于只改变了系数的更新方式，每次迭代仍然只产生一个原子，在信号维数高的情况下需要指定稀疏度进行多次迭代，而稀疏度的指定往往具有不确定性，这在一定程度上降低了算法的效率。

1.3 相关正交匹配追踪

为了在保证精度的前提下减少算法的迭代次数，同时使算法具有较高的重构效率，本文提出了改进的OMP算法——COMP算法。该算法在第k次迭代中，计算r(k-1)与D的内积找到使最大的原子Dk和次大的原子d并分别计算与r(k-1)的相关系数c0和c1，然后合并Dk和d并计算合并后原子与r(k-1)的相关系数 c2，若满足c2≥max（c0，c1），则将合并后的原子作为一个新原子重新赋给Dk；若不满足则取消合并，保留Dk。寻找下一个与r(k-1)内积最大的原子替代d重复上述过程，直到满足合并的终止条件。每合并完一个新原子后，进行下一次迭代，系数的更新方式与OMP算法相同，即α =D+y，计算残差r(k)=y-Dkα(k)，直到满足算法的终止条件，迭代停止，输出最优解。

COMP算法相对于OMP算法：一方面，前者保留了OMP算法中系数的更新方式，但却避免了稀疏度设置的不确定性，只需设置迭代次数就可使算法收敛；另一方面，每次迭代后产生的新原子是由多个与信号相关度较高的原子线性叠加而成，且新原子与信号的相关度大于组成它的每一个原子的相关度，在一定程度上提高了稀疏表示精度。

另外，考虑到构造的离散小波字典是超完备的，在合并过程中只有部分原子与残差的相关系数较大，所以不需要无限合并。据此，原子合并的终止条件为：参与合并的原子数等于算法的迭代次数。算法流程（图1）描述如下。

图1COMP算法流程Fig.1 Flow chart of COMP angorithm

初始化：设置k=0；迭代次数为K；残差阈值为ε0；初始解α(0)=0；初始残差为r(0)=y；

（1）主要迭代。每次k加1，并执行下列步骤：①对所有的 i，计算②将取最大值时对应的原子记为Dk，计算Dk与r(k-1)的相关系数c0，令j=0；③令max（）=0，i=1，2，…，n。将取最大值时对应的原子记为dj+1，计算dj+1与 r(k-1)的相关系数 c1；④=Dk+dj+1，计算与r(k-1)的相关系数 c2；⑤若 c2≥max（c0，c1），则 Dk=；否则执行⑥；⑥j←j+1，若j＜K，则返回③；否则执行（2）；

（2）更新临时解。令α(k)=D+ky；

（3）更新残差。计算r(k)=y-Dkα(k)；

（4）停止条件。如果||r(k)||2≤ε0，或k=K则停止迭代，否则返回主要迭代。

（5）输出。在k次迭代以后获得的优化解α(k)。

2 仿真与实验

2.1 数值仿真

为验证所提方法的有效性，将该方法用于实现强噪声污染下冲击特征的有效提取。在故障发生的早期，滚动轴承的振动信号为由故障产生的冲击成分、转频及其倍频等谐波成分和噪声组成的信号，因此，构造仿真信号数学模型为y(t)=h(t)+s+n(t)，其中，h(t)为冲击成分，s(t)为谐波成分，n(t)为高斯白噪声，具体如下：

式中，α为衰减指数，α=2 000；T0为初始位置，T0=0.025 s；f0为故障频率，f0=20 Hz；T 为故障周期，T=0.05 s；fz为固有频率，fz=2 kHz；fr为转频，fr=10 Hz，fs为采样频率，fs=10 kHz；N为采样点数，N=4 096。

所添加噪声为高斯白噪声，均方差为0.138 5。

冲击成分h（t）的时域波形见图2a，仿真信号y（t）的时域波形见图2b，可以看出，冲击成分几乎淹没在噪声与谐波中。直接对仿真信号进行能量算子解调，得到包络谱（图3），在图3中只能观察到f0，其余分量均被噪声淹没。

图2 仿真信号Fig.2 Simulation signals

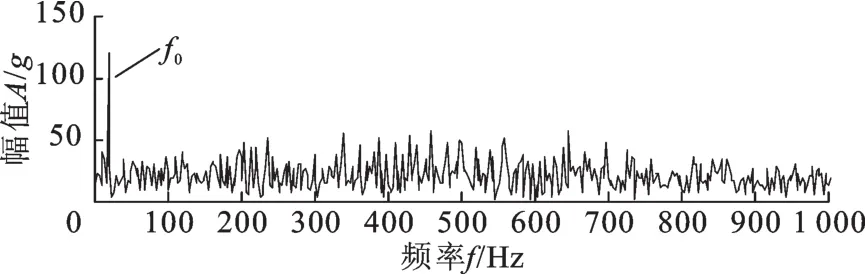
图3 仿真信号包络谱Fig.3 The envelope spectrum of simulation signal

利用本文所提方法对仿真信号y（t）进行处理，迭代次数设置为2，得到结果见图4a，可以看出除了0.17 s左右的冲击特征未被检测到外，其余冲击都被准确无误地提取出来。对提取到的冲击信号做能量算子解调，得到包络谱见图4b，可以看出故障频率f0=20 Hz及其倍频很明显，实现了冲击故障特征的有效提取。

图4 本文方法对冲击成分的分析结果Fig.4 Analysis results of the method herein for impulse signal

2.2 实验验证

本文采用齿轮轴承故障诊断综合实验平台模拟滚动轴承外圈故障，进一步验证COMP算法的有效性和实用性。其中，滚动轴承外圈故障参数见表1，实验所用轴承的详细参数见表2，轴承损伤照片见图5。

表1 滚动轴承故障类型及说明Tab.1 Failure type and description of rolling bearing

表2 滚动轴承参数Tab.2 Parameters of rolling bearings

图5 滚动轴承外圈故障Fig.5 Outer race fault of rolling bearing

实验中，电机转频为fr=7.84 Hz，采样频率为fs=12 800 Hz，数据长度 N=8 000，结合表2，计算得到轴承外圈故障特征频率为f0=39.24 Hz。从实验台采集得到的时域波形见图6a，其对应的频谱见如图6b。

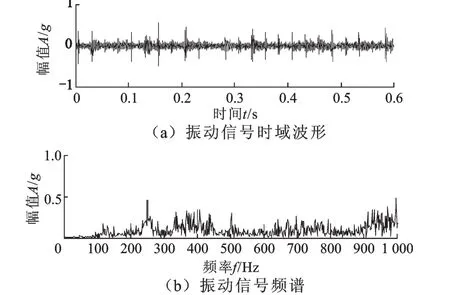
图6 振动信号时域波形及频谱Fig.6 Waveform and frequency spectrum of vibration signal

由图6可以看出，时域波形含有不太明显的周期性冲击成分，而且在频谱图中，由于背景噪声的影响，无法检测到滚动轴承故障特征。

利用本文方法对图6a所示振动信号进行处理，得到处理结果如图7所示。由图7a可以看出，振动信号经过本文方法处理之后，由故障缺陷引起的冲击特征大部分被提取出来，在一定程度上减少了噪声的影响。由图7b可以看出，显现出的特征频率与滚动轴承外圈故障特征频率相符，且倍频成分明显。实验结果表明，本文方法可有效实现滚动轴承故障特征提取与诊断。

图7 本文方法对重构信号的分析结果Fig.7 Analysis results of the method herein for reconstructed signal

3 工程应用

对某风电场的多台风电机组进行振动检测，发现10号风力机组的发电机驱动端轴承振动明显。为进一步确定其原因，需对该机组的振动信号进行深入分析。风电机组传动系统振动传感器分布见图8。其中，轴承型号为6332M_FAG，发电机转频为fr=20 Hz，采样频率为fs=12 800 Hz，数据长度N=8 000。详细的滚动轴承参数列于表3。

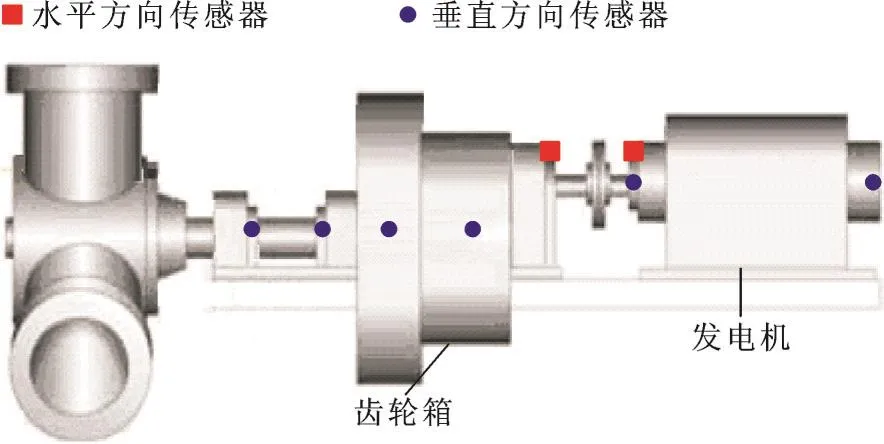
图8 风电机组振动传感器的分布图Fig.8 Vibration sensor distribution of wind turbines

表3 风发机组中发电机轴承参数Tab.3 Parameters of bearings in wind turbines

发电机驱动端轴承振动信号的时域波形及其频谱见图9a和图9b，可以发现，时域波形振动杂乱，而频谱图中除了明显的转频分量，难以发现与轴承故障相关的特征信息。对该振动信号进行能量解调算子处理，得到的包络谱见图9c。在包络谱中，出现了与轴承外圈故障特征频率f0=109 Hz相符的谱峰值，但由于背景噪声的影响，特征识别精度不高。

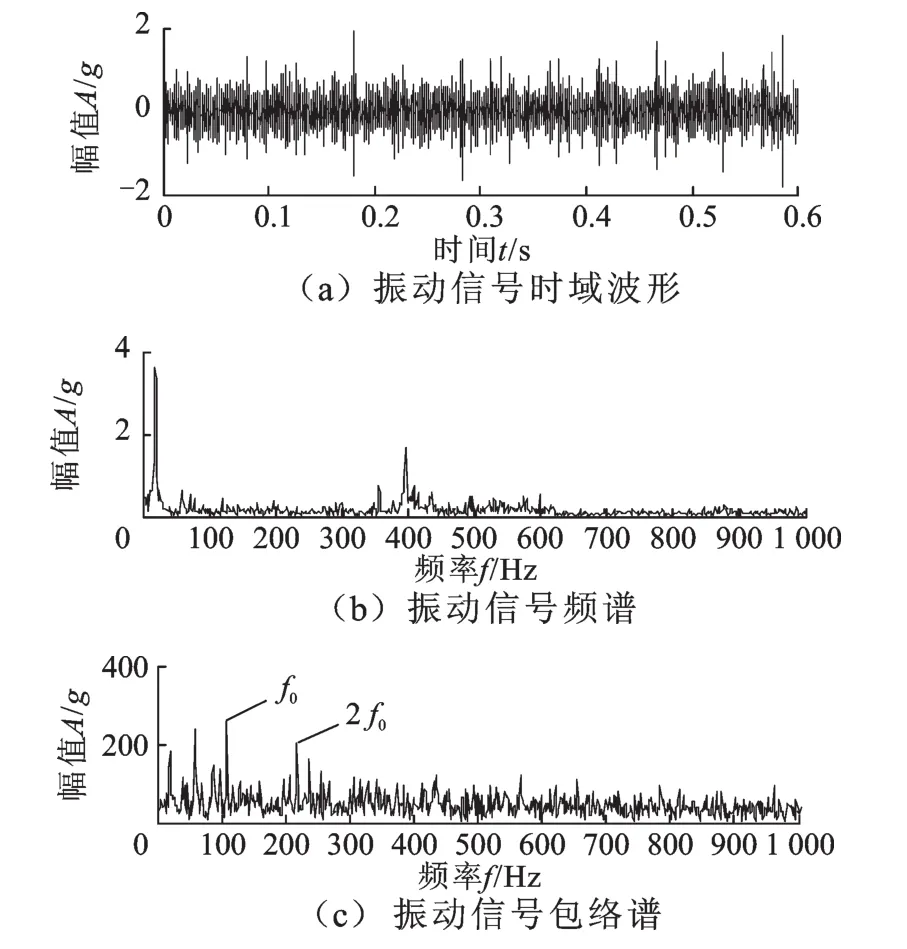
图9 振动信号分析结果Fig.9 Analysis results of vibration signal

利用本文方法处理图9a所示的振动信号，设置迭代次数为9，得到重构信号（图10），对重构信号进行能量算子解调得到包络谱（图11）。从包络谱可以看出，轴承故障特征频率f0及其倍频非常明显，并且受噪声影响较小。这表明，风电机组发电机驱动端轴承外圈出现损伤，应定期关注。

图10 重构信号时域波形Fig.10 Waveform of reconstructed signal

图11 重构信号包络谱Fig.11 Envelope spectrum of reconstructed signal

为进一步验证COMP算法的优越性，现对图9a所示信号利用OMP算法进行稀疏分解。设置OMP算法迭代次数（稀疏度）为9，得到重构信号包络谱（图12）。由图11和图12对比可知，图12中轴承故障信息依然被噪声淹没，识别效果较差。因此，两种算法在迭代次数相同的情况下，COMP算法能够取得更高的特征提取精度。

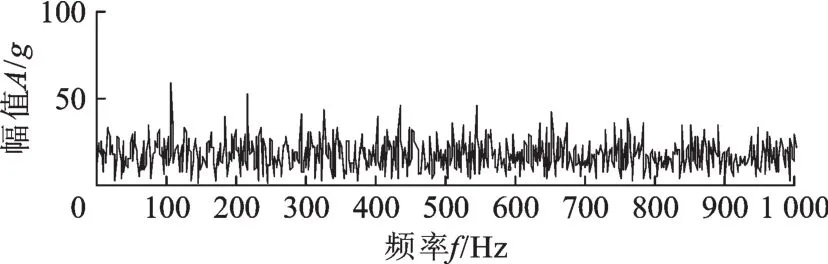
图12 OMP算法得到的重构信号包络谱Fig.12 Envelope spectrum of reconstructed signal

通过增大OMP算法的迭代次数也能从信号中提取出冲击成分并对其产生一个稀疏表示，但是COMP算法能在较少的迭代次数内达到最优分解效果，并且免去了稀疏度设置的不确定性，而OMP算法却不具备这种优势，所以在滚动轴承振动信号稀疏分解中，COMP算法的效率明显高于OMP算法，有利于滚动轴承故障特征的准确提取与诊断。

4 结论

（1）与OMP算法相比，COMP算法可提高信号的重构效率；而本文提出的基于COMP算法的稀疏诊断方法可有效实现滚动轴承故障诊断，提高故障诊断的准确性。

（2）工程应用表明，在对振动信号进行稀疏诊断时，COMP算法较OMP算法能在较少的迭代次数内收敛，消除了稀疏度设置的不确定性对特征提取精度的影响，且COMP算法的优越性在处理高维信号时更突出。

（3）在本文提出的故障稀疏诊断方法中，没有进行信号降噪处理，仅利用了稀疏分解本身对噪声的不匹配性来降低噪声干扰。同时，选定的字典结构固定，若信号受谐波干扰严重，直接使用本方法可能不会取得最佳效果，可以考虑在本方法前做谐波干扰的剔除处理。因此，找到一种能够与稀疏分解完美契合的降噪和谐波剔除方法以及构造自适应字典将是下一步的研究重点。

［1］ 刘波，贺志佳，金昊.风力发电现状与发展趋势［J］.东北电力大学学报，2016，36（2）：7⁃13.LIU Bo，HE Zhijia，JIN Hao.Wind Power Status and Development Trends［J］.Journal of Northeast Dianli University，2016，36（2）：7⁃13.

［2］ 李垚，朱才朝，陶友传，等.风电机组可靠性研究现状与发展趋势［J］.中国机械工程，2017，28（9）：1125⁃1133.LI Yao，ZHU Caichao，TAO Youchuan，et al.Re⁃search Status and Development Tendency of Wind Turbine Reliability［J］.China Mechanical Engineer⁃ing，2017，28（9）：1125⁃1133.

［3］ 陈雪峰，郭艳婕.风电装备振动监测与诊断［M］.北京：科学出版社，2016：191.CHEN Xuefeng，GUO Yanjie.Wind Power Equip⁃ment Vibration Monitoring and Diagnosis［M］.Bei⁃jing：Science Press，2016：191

［4］ COIFMAN R R，WICKERHAUSER M V.Entropy⁃based Algorithms for Best Basis Selection［J］.IEEE Transactions on Information Theory，1992，38（2）：713⁃718.

［5］ CHEN S S，DONOHO D L，SAUNDERS M A.Atomic Decomposition by Basis Pursuit［J］.SIAM Review，2006，43（1）：129⁃159.

［6］ MALLAT S G，ZHANG Z.Matching Pursuits with Time⁃ Frequency Dictionaries［J］.IEEE Transactions on Signal Processing，1993，41（12）：3397⁃3415.

［7］ PATI Y C，REZAIIFAR R，KRISHNAPRASAD P S.Orthogonal Matching Pursuit：Recursive Function Approximation with Applications to Wavelet De⁃composition［C］//The 27th Asilomar Conference on Signals，Systems and Computers.Pacific Grove，1993：40⁃44.

［8］ 王林，蔡改改，高冠琪，等.基于改进MP的稀疏表示快速算法及其滚动轴承故障特征提取应用［J］.振动与冲击，2017，36（3）：176⁃182.WANG Lin，CAI Gaigai，GAO Guanqi，et al.Fast SparseRepresentationAlgorithm BasedonIm⁃proved MP and Its Applications in Fault Feature Ex⁃traction of Rolling Bearings［J］.Journal of Vibration and Shock，2017，36（3）：176⁃182.

［9］ 孙占龙，佟庆彬.基于ADMM字典学习的滚动轴承振动信号稀疏分解［J］.中国机械工程，2017，28（3）：310⁃315.SUN Zhanlong，TONG Qingbin.Sparse Decomposi⁃tion of Vibration Signals of Rolling Bearings Based on ADMM Dictionary Learning［J］.China Mechani⁃cal Engineering，2017，28（3）：310⁃315.

［10］ 崔玲丽，莫代一，邬娜.并联基追踪稀疏分解在齿轮箱弱故障诊断中的应用［J］.仪器仪表学报，2014，35（11）：2633⁃2640.CUI Lingli，MO Daiyi，WU Na.Application of Sparse Signal Decomposition Using Dual⁃BP in Gear⁃box Weak Fault Diagnosis［J］.Chinese Journal of Scientif⁃ic Instrument，2014，35（11）：2633⁃2640.

［11］ 张晗，杜朝辉，方作为，等.基于稀疏分解理论的航空发动机轴承故障诊断［J］.机械工程学报，2015，51（1）：97⁃105.ZHANG Han，DU Zhaohui，FANG Zuowei，et al.Sparse Decomposition Based Aero⁃engine’s Bear⁃ing Fault Diagnosis ［J］.Journal of Mechanical Enigneer，2015，51（1）：97⁃105.

［12］ ELAD M.Sparse and Redundant Representation：Theory and Its Application in Signal and Image Processing［M］.Berlin：Springer，2010：28.*