绿泥石的球磨特性及其破裂参数

赵瑞超，韩跃新，何明照，李艳军



绿泥石的球磨特性及其破裂参数

赵瑞超1, 2，韩跃新1，何明照3，李艳军1

(1. 东北大学 资源与土木工程学院，沈阳 110819；2. 内蒙古科技大学 矿业与煤炭学院，包头 014010；3. CITIC Pacific Mining Management Pty Ltd., 45 St. Georges Terrace, Perth, WA6000, Australia)

在相同的球磨条件下，对4种窄粒级的绿泥石进行实验室分批湿式球磨试验。结果表明：4种粒级绿泥石的磨矿动力学都遵循一阶磨矿动力学，球磨0.25~0.5 mm的绿泥石时获得最大的破碎速率函数S=0.35 min−1，正常的破碎粒级范围应该小于0.5 mm；在较短的磨矿时间内，0.25~0.5 mm绿泥石的细粒级产出具有明显的零阶产出特征；采用-算法获得0.25~0.5 mm粒级绿泥石的累积破碎分布函数B，利用磨矿总体平衡动力学模型，对粒级为0.25~0.5 mm的绿泥石进行球磨模拟仿真计算，试验结果与模拟仿真结果高度一致。

绿泥石；湿式球磨；总体平衡动力学模型；破碎速率；累积破碎分布函数

磨矿作业是物料破碎作业的继续，是物料入选前准备的最后一道工序[1]。尽管近十多年来，超细粉碎及分级技术迅速发展，相继开发高速冲击粉碎机、振动磨机、搅拌磨机、气流磨机、高压辊磨机等磨矿设备，但上述磨矿加工方式均无法在规模化粉体加工生产方面替代球磨机，尤其是在粗磨作业中，球磨机仍然是磨矿作业中应用最广泛的设备[2−3]。

绿泥石是一族层状结构硅酸盐矿物的总称，其化学组成可表示为Y3[Z4O10](OH)2·Y3(OH)6，化学式中Y主要是Mg2+、Fe2+、Al3+和Fe3+，Z主要是Si和Al；晶体属单斜、三斜或正交(斜方)晶系。它是一些变质岩的造岩矿物，分布较广，且硬度较低(莫氏硬度2~3)，在其他金属或非金属矿物选别提纯过程中，绿泥石是一种易泥化的脉石矿物，一直都是重点研究对象[4−5]。另外，当绿泥石矿石矿物达到一定工业要求时，可以作为一种重要的工业矿物原料，用于塑胶、造纸、医药、阻燃、牙膏等行业[6]。

针对球磨过程中易泥化的绿泥石磨矿特性，国内研究文献相对较少，本文作者使用实验室小型球磨机，采用分批湿式球磨工艺对4种窄粒级的(1.19~2、0.5~1.19、0.25~0.5和0.15~0.25 mm)绿泥石球磨特性及其破裂参数进行试验研究，利用总体平衡分批磨矿微分动力学数学模型(PBM)和-算法，研究该窄粒级绿泥石单独球磨时，绿泥石的破裂参数(破裂速率函数S和累积破裂分布函数B)特性，通过球磨试验结果建立绿泥石矿样的磨矿动力学数学模型。

1 实验

1.1 矿样原料的制备

绿泥石矿样取自辽宁海城市瑞通矿业有限公司，绿泥石经水洗去矿石表面的矿泥，自然晾干后采用实验室颚式破碎机−台式圆盘破碎机破碎至2 mm以下，并取样对其进行化学多元素和XRD分析，然后使用标准套筛在振筛机上筛分20 min，获得1.19~2、0.5~1.19、0.25~0.5、0.15~0.25和＜0.15 mm5个粒级产品。绿泥石的化学多元素分析和XRD分析结果分别见表1和图1。由表1和图1分析可知，绿泥石的纯度高达95%以上，绿泥石中含有少量的菱沸石(CaAl2Si4O12∙6H2O)。

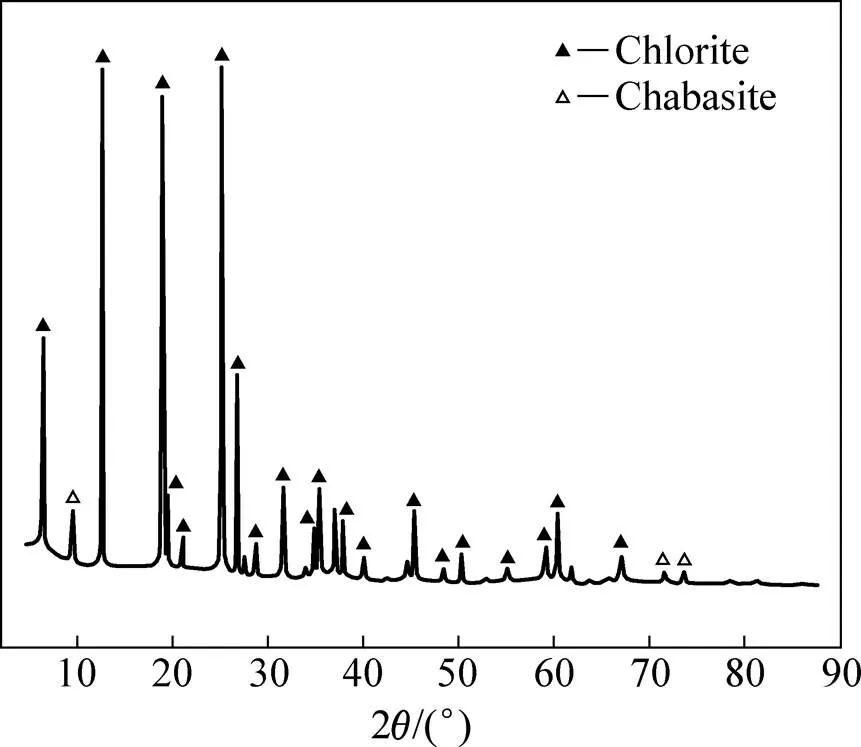
图1 绿泥石单矿物的XRD谱

1.2 试验方法

采用100 mm×150 mm实验室小型滚筒式球磨机进行分批开路湿式球磨试验。所用滚筒球磨机的容积为1 L，磨矿介质为球并以体积填充率为基准，即料球比(物料体积与球间隙体积之比)为0.6。在试验过程中，保持滚筒转速为105 r/min，即磨机的转速率为0.75，球的填充率为0.4，磨矿球介质总质量为1.86 kg，球磨介质的直径为25、20和15 mm，球径的大小配比为3:3:4，磨矿浓度为70%。对每次的磨矿产品进行干湿联合粒度筛析，根据各粒级的产品产率进行理论计算，获得绿泥石的破裂参数。

2 磨矿总体平衡动力学模型及特征参数的求解

基于磨矿过程中物料平衡原理，根据破碎速率函数和破碎分布函数的概念和一阶动力学磨矿方程，1965年，REID[7]提出了时间连续−颗粒离散磨矿动力学数学模型：总体平衡动力学模型(PBM)。该磨矿动力学模型广泛应用于磨矿过程中的数值模拟仿真、球磨机的优化和设计以及球磨工艺参数确定[8−10]，另外，也可以揭示球磨过程中的破碎机制[11−12]，其数学表达式如下：

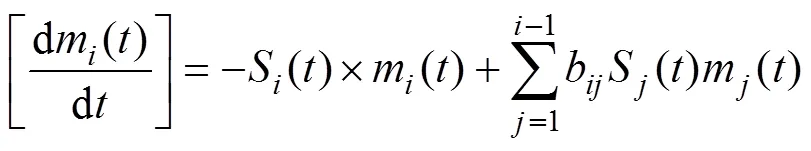
式中：=1，2，3，…，；=1，2，3，…，(＞)；m()为时刻第粒级的含量(产率)；S为破裂速率函数，min−1；b为破裂分布函数，表示从给料第粒级粉碎至产品中第粒级的产率。为了方便表述和计算，总体平衡动力学模型中的破碎分布函数b常用累积破碎分布函数B表示：

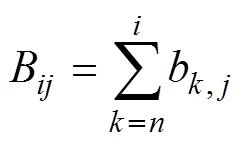
因此，B表示为给料中第粒级破碎后形成的产品中小于粒级的累积产率。对于最粗粒级物料或者窄级别单粒级物料磨碎时，即第一粒级物料=1，式(1)可以简化为：

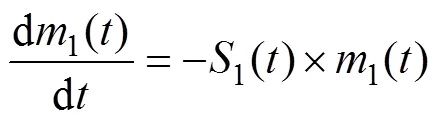
式中：1()为时刻第一粒级的质量分数(产率)；1()为第一粒级的破裂速率函数。当破裂速率函数1与磨矿时间无关，即物料的磨矿过程符合一阶线性动力学模型时，对于单粒级物料可知1(0)=1，将式(3)积分求解可以获得：

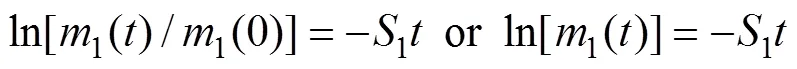
式(4)就是常见的磨矿一阶动力学方程。如果将试验结果1()的半对数作为磨矿时间的函数进行画坐标图，它们的关系应为直线关系，且直线的斜率即为破碎速率函数1。

为求该方程式(1)的解，首先必须求出中参数S和b。关于参数S和b的特性及其测定，许多学者做了详细的研究计算，提出许多参数估算方法[13−16]，本文作者主要采用KAPUR的-算法[13, 16]。-算法的基本指导思想为将总体平衡动力学方程转换成、两个函数，使之能迭代运算，以便于用计算机求解参数的值。这个方程推导过程比较繁琐，具体过程可以参考相关文献[16]。当原料为单粒级(=1)时，可以得出：

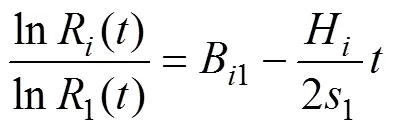
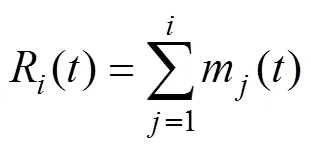
3 结果与讨论

3.1 不同粒级绿泥石的破裂速率函数

对4种不同单粒级(1.19~2、0.5~1.19、0.25~0.5和0.15~0.25 mm)绿泥石进行分批湿式球磨试验。试验数据结果代入式(4)，计算结果如图2所示。

由图2可以看出，球磨单粒级绿泥石时(=1)，在试验的粒级范围内，绿泥石的磨矿动力学行为符合一阶线性规律，即破裂速率函数S与磨矿时间无关，每条直线的斜率为该粒级绿泥石的破碎速率函数S，即绿泥石的磨矿动力学符合一阶磨矿动力学，4种不同单粒级1.19~2、0.5~1.19、0.25~0.5和0.15~0.25 mm的绿泥石的破碎速率分别为0.09、0.16、0.35和0.15 min−1；另外，由图2可以发现，当=0时，各粒级绿泥石的动力学曲线延长接近通过零点。对于0.25~0.5 mm粒级的绿泥石，当=0时，纵坐标的截距绝对值最大，即ln[1()/1(0)]=0.045，可以计算得出，[1()/1(0)]≈0.956。理论上认为0.25~0.5 mm粒级绿泥石中仅含有少量细粒级绿泥石，由此可以认为绿泥石各粒级筛分得比较完全。

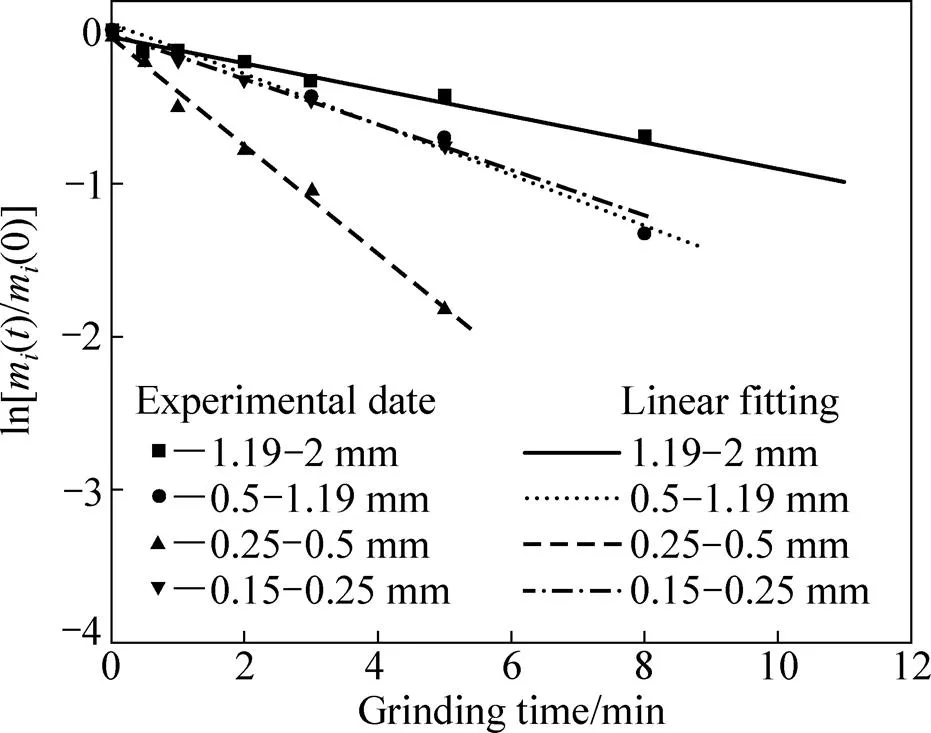
图2 不同粒级绿泥石的磨碎行为

为了更清晰地表达不同给料粒级对绿泥石破裂速率函数S的影响，图3给出了绿泥石破碎速率函数(或破碎速率)S与绿泥石粒级的关系。

由图3可知，给料粒级为0.25~0.5 mm时，破碎速率函数S取得最大值0.35 min−1。当小于0.5 mm时，破碎速率函数S随着粒度尺寸的减小而降低；当大于0.5 mm时，破碎速率函数S随着粒度尺寸的增加而降低。一般认为：在正常的球磨条件下，粗矿块的裂缝及裂纹相对较多，力学性能(包括硬度、韧性、解理及架构缺陷等)降低比较明显，随着矿块粒度的变小，裂缝及裂纹逐渐消失，强度逐渐增大，力学的均匀性增高，故球磨细粒级物料相对比较困难，也就是说破裂速率函数S会随着磨矿粒级的减小而降低。本试验条件下，绿泥石在小于0.5 mm粒级为正常的破碎范围，当绿泥石颗粒的粒度超过0.5 mm时，破裂速率函数S会随着给矿物料粒级的增大而降低，出现这种非正常磨碎现象，主要是由于物料的粒度过于粗大，在磨矿过程中球介质无法将物料夹在球介质之间，获得有效地冲击和研磨，导致在球磨过程中粗粒级物料不能正常磨碎[17−19]。因此，该磨矿条件下，对绿泥石的正常球磨粒级范围应该小于0.5 mm，以下的球磨试验使用最大破碎速率值时的粒级，即0.25~0.5 mm粒级的绿泥石进行下一步球磨试验。

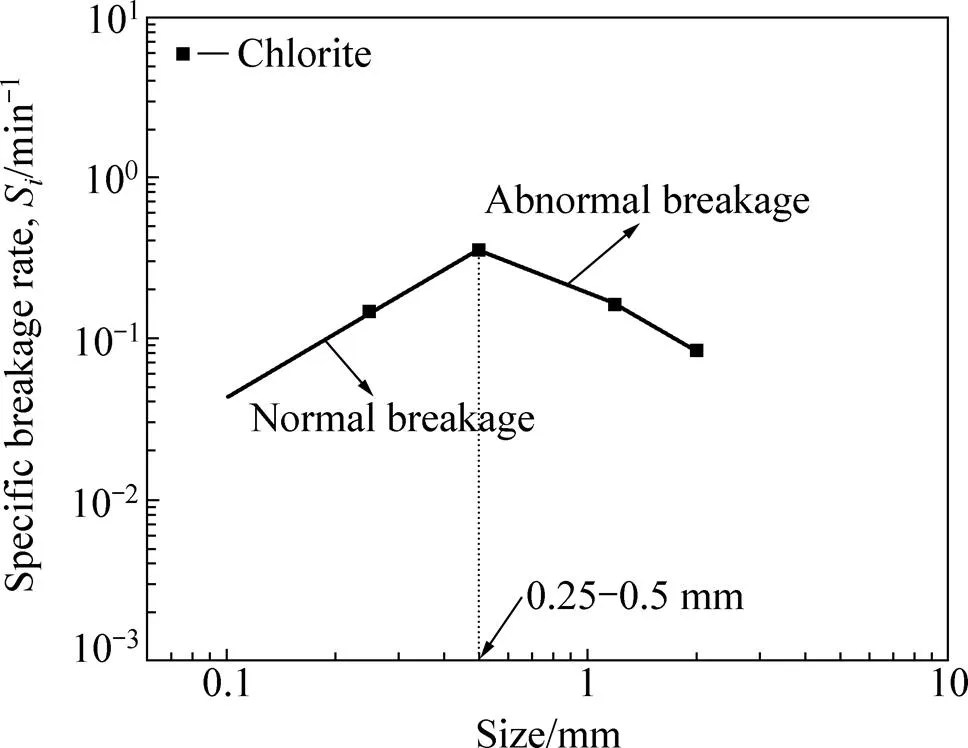
图3 给料粒度与破碎速率Si的关系

3.2 绿泥石的细粒级零阶产出特征

试验结果表明，物料在较短的磨矿时间内均具有相当显著的细粒级零阶产出特征[13, 20]，即磨矿速率为常数：

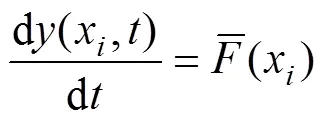
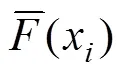
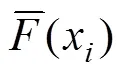
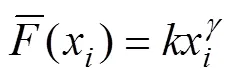
式中：和均为常数，图5是对式(7)中指数常数的线性回归。

由图5可以获得绿泥石磨碎时常数和的值分别为0.204和0.369。通常对于某一物料，在正常的磨碎条件下，不管磨机尺寸、磨矿条件(如装球率、转速率、装矿量、球介质组成等均不相同)和磨矿环境(包括有无另一组分存在、另一组分的种类、组分的配比)如何变化，其值是相同的。即值只与物料本身的碎裂特性有关[21−22]，这里获得的常数是否正确，将会在球磨自然粒级分布的绿泥石中进行验证。

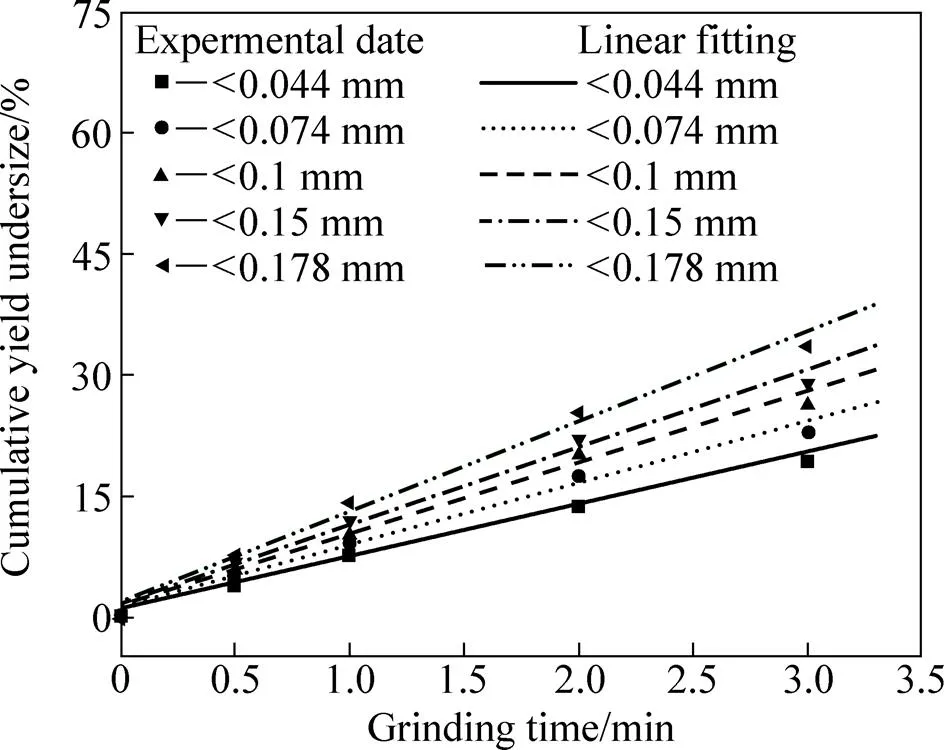
图4 0.25~0.5 mm绿泥石细粒产出特征

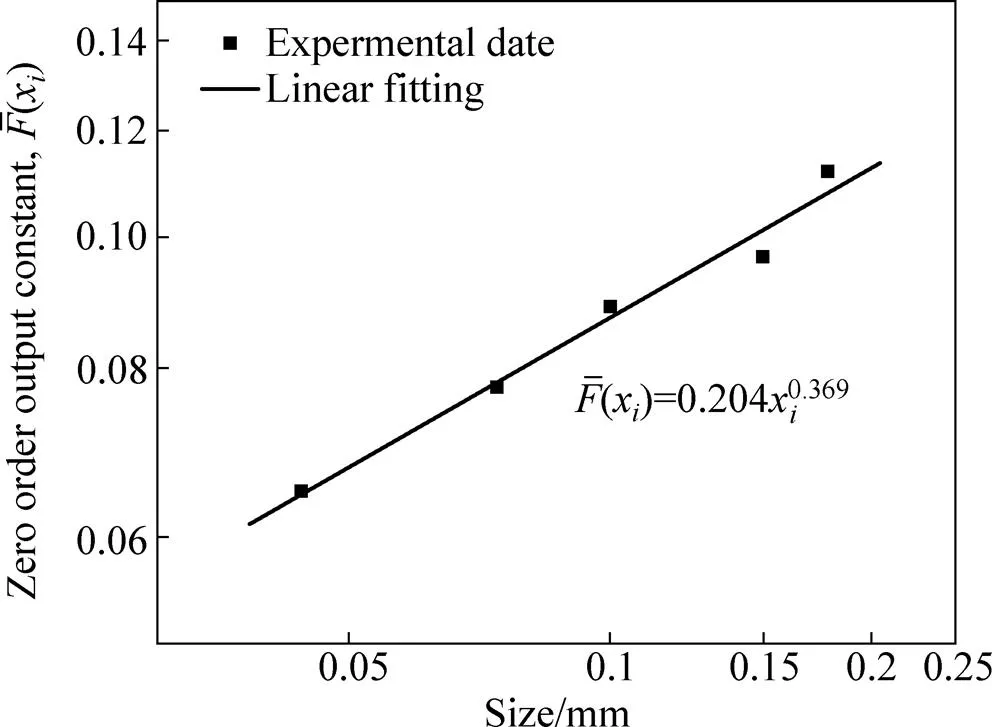
图5 短时间磨矿时赤铁矿的与xi的关系

3.3 绿泥石的累积分布函数

针对0.25~0.5 mm粒级的绿泥石球磨0.5、1、2和3 min的球磨试验结果采用-算法，可以获得该粒级绿泥石的球磨累积破碎分布函数B。试验数据代入式(5)，试验结果如图6所示。

由图6可知，当横坐标=0时，在纵坐标上的截距就是累积破碎分布函数B1(≥3)，即取每个粒级拟合直线在纵坐标ln(R)/ln(1)的截距，根据B1的定 义[8, 16]，11=1，21=1，根据-算法获得0.25~0.5 mm粒级绿泥石累积破碎分布函数B(=1)结果如图7所示。图7中也给出了累积破碎分布函数B的拟合方程，可以获取该粒级绿泥石破碎到任意粒级的累积破碎分布函数值。

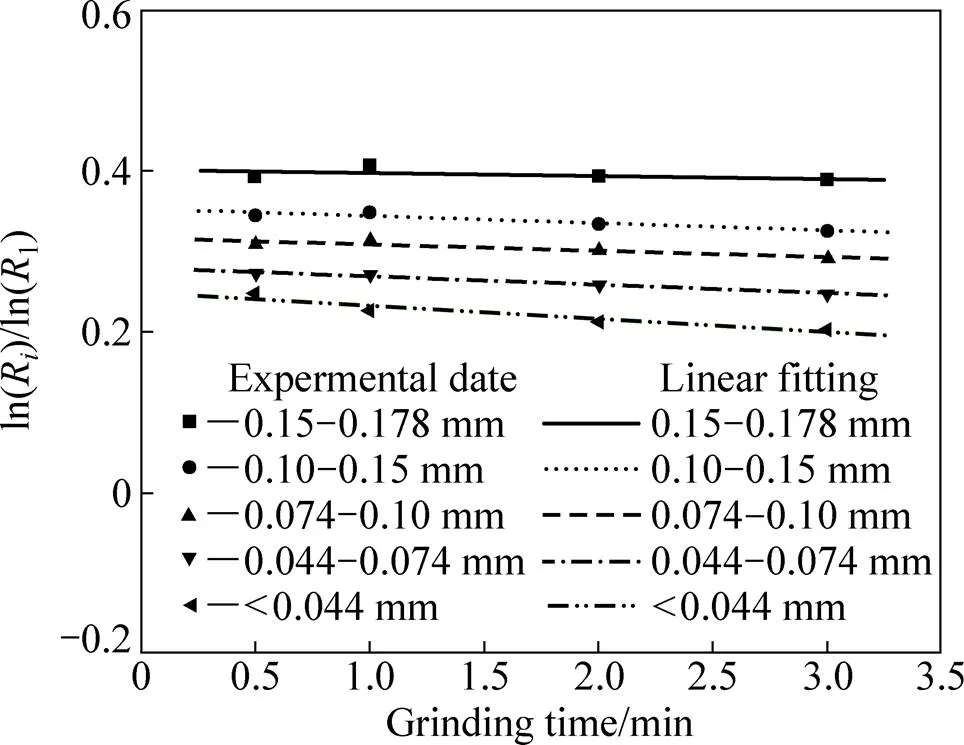
图6 采用G-H算法绘制的0.25~0.5 mm绿泥石湿式磨矿试验结果图

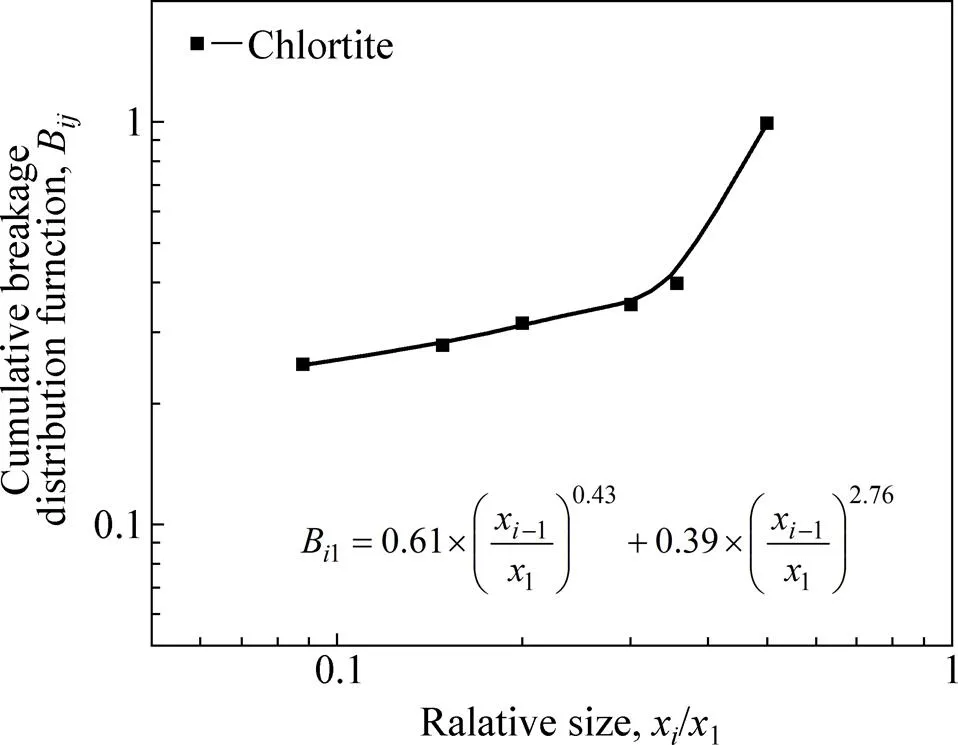
图7 绿泥石的累积分布函数(i≥2，点—试验数据，线—数据拟合结果)

3.4 绿泥石的模拟计算结果

0.25~0.5 mm粒级绿泥石在球磨过程中，破裂速率函数1由图2或图3给出，采用-算法计算获得0.25~0.5 mm绿泥石的累积破裂分布函数B1(见图7)，磨矿总体平衡动力学数学模型的仿真计算来考查这些破裂参数是否成立。在假定上述各破裂参数计算公式成立的前提下，代入式(1)模拟仿真，此时，绿泥石为单粒级矿物(=1)，式(1)很容易被积分求解获得。图8给出了模型仿真结果和试验结果。

由图8可知，随着磨矿时间的增加，各细粒级绿泥石的产率也随着增加，当磨矿时间由0.5 min增加到3 min时，＜0.044 mm粒级的绿泥石试验结果产率由原来的2.8%增加到了19.3%。当球磨1 min时， ＜0.044 mm、＜0.074 mm、0.010 mm 3个粒级的绿泥石负累积产率试验结果分别为10.64%、12.54%、14.39%。从图8中也可以发现，该球磨模拟仿真计算与试验结果的最大偏差仍小于2%，0.25~0.5 mm的绿泥石也可以获得了比较满意的模型仿真结果。这也说明前述假设是成立的，该粒级的绿泥石在磨矿过程中，其碎裂参数是正确的，可以认为该数学仿真模型能对任意时刻0.25~0.5 mm绿泥石的磨矿产品粒度分布进行理论分析计算。

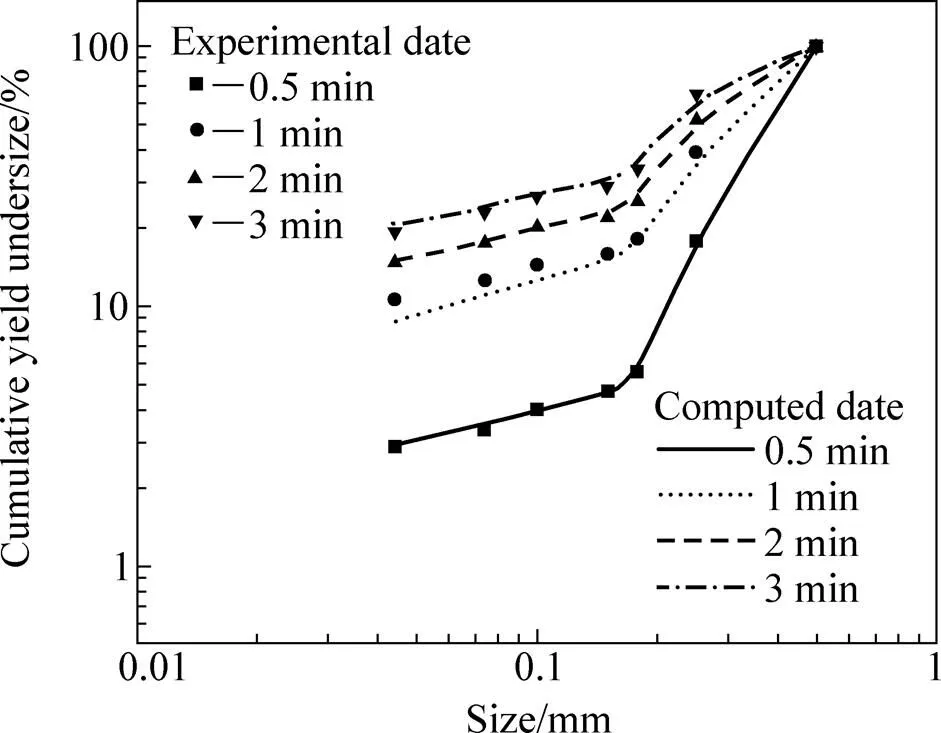
图8 0.25~0.5 mm绿泥石试验结果与模拟计算结果

4 结论

1) 对4个窄粒级的绿泥石球磨试验，结果发现它们都符合一阶磨矿动力学方程。每个粒级在球磨过程中，破碎速率函数S是常数，与磨矿时间无关。在相同的条件下，给料粒级为0.25~0.5 mm时，该粒级绿泥石的破碎速率函数S取得最大值0.35 min−1，在该球磨条件下，绿泥石的正常球磨粒级范围应该小于0.5 mm。

2)球磨粒级为0.25~0.5 mm的绿泥石时，试验结果表明：在较短的磨矿时间内，细粒级的产出具有明显的零阶产出特征，并获得了绿泥石单矿物零阶产出特征参数值为0.369；同时，根据球磨试验结果，采用-算法获得绿泥石累积破碎分布函数B。

3) 根据所获绿泥石的破碎特征参数(破碎速率函数和累积破碎分布函数)对0.25~0.5 mm粒级的绿泥石进行仿真模拟计算。模拟计算结果表明：球磨0.25~0.5 mm粒级绿泥石的试验结果与模拟仿真计算结果最大误差小于2%，获得了比较满意的一致性，可以认为前述计算获得的磨矿破裂参数(破碎速率函数S和累积破碎分布函数B)是正确的。

[1] 刘 琨. 金属矿磨矿设备研究与应用新进展[J]. 中国资源综合利用, 2014(3): 40−42. LIU Kun. The research in the research & application of metal mine grinding equipment[J]. China Resources Comprehensive Utilization, 2014(3): 40−42.

[2] 赵 敏, 卢亚平, 潘英民. 粉碎理论与破碎设备发展评述[J]. 矿冶, 2001, 10(2): 36−41. ZHAO Min, LU Ya-ping, PAN Ying-min. Development of comminution theory and equipment[J]. Mining and Metallurgy, 2001, 10(2): 36−41.

[3] RAMASAMY M, NARAYANAN S S, RAO C. Control of ball mill grinding circuit using model predictive control scheme[J]. Journal of Process Control, 2005, 15(3): 273−283.

[4] 张宇平, 黄可龙, 刘素琴. 反浮选法分离粉石英和斜绿泥石及其机理[J]. 中南大学学报(自然科学版), 2007, 38(2): 285−290. ZHANG Yu-ping, HUANG Ke-long, LIU Su-qin. Separation of clinochlore from powder quartz by reverse flotation and its mechanism[J]. Journal of Central South University (Science and Technology), 2007, 38(2): 285−290.

[5] 冯 博, 朱贤文, 王金庆, 汪惠惠, 王鹏程. 高分子抑制剂在绿泥石浮选中的双重作用[J]. 矿物学报, 2016, 36(1): 115−118. FENG Bo, ZHU Xian-wen, WANG Jin-qing, WANG Hui-hui, WANG Peng-cheng. The dual role of polymeric depressant in chlorite flotation[J]. Acta Mineralogica Sinica, 2016, 36(1): 115−118.

[6] 宋春振, 李树敏, 冯惠敏, 苏昭冰. 我国绿泥石资源特征及其工业利用[J]. 中国非金属矿工业导刊, 2009(5): 57−59. SONG Chun-zhen, LI Shu-min, FENG Hui-min, SU Zhao-bing. The characteristics and its industrial use of China’s chlorite mineral resources[J]. China Non-Metallic Mining Industry Herald, 2009(5): 57−59.

[7] REID K J. A solution to the batch grinding equation[J]. Chemical Engineering Science, 1965, 20(11): 953−963.

[8] AUSTIN L G, JULIANELLI K, SOUZA A S D, SCHNEIDER C L. Simulation of wet ball milling of iron ore at Carajas, Brazil[J]. International Journal of Mineral Processing, 2007, 84(1/4): 157−171.

[9] OZKAN A, YEKELER M, CALKAYA M. Kinetics of fine wet grinding of zeolite in a steel ball mill in comparison to dry grinding[J]. International Journal of Mineral Processing, 2009, 90(1/4): 67−73.

[10] CAPECE M, BILGILI E, DAVE R. Identification of the breakage rate and distribution parameters in a non-linear population balance model for batch milling[J]. Powder Technology, 2011, 208(1): 195−204.

[11] DANHA G, HILDEBRANDT D, GLASSER D, BHONDAYI C. Application of basic process modeling in investigating the breakage behavior of UG2 ore in wet milling[J]. Powder Technology, 2015, 279: 42−48.

[12] HOUNSLOW M. The population balance as a tool for understanding particle rate processes[J]. Kona Powder & Particle Journal, 1998, 16: 179−193.

[13] 陈丙辰. 磨矿原理[M]. 北京: 冶金工业出版社, 1989. CHEN Bing-chen. Grinding principle[M]. Beijing: Metallurgical Industry Press, 1989.

[14] AUSTIN L G. A discussion of equations for the analysis of batch grinding data[J]. Powder Technology, 1999, 106(1/2): 71−77.

[15] HERBST J A, MIKA T A. Mathematical simulation of tumbling mill grinding: An improved method[J]. Rudy, 1970, 18: 70−75.

[16] KAPUR P C. Modelling of tumbling mill batch processes[M]. Crushing and Grinding Process Handbook. Chichester: Wiley, 1987.

[17] AUSTIN L G, KLIMPEL R R, LUCKIE P T. Process Engineering of size reduction: Ball milling[C]//New York: Society of Mining Engineers of the AIME, 1984.

[18] TANGSATHITKULCHAI C. Acceleration of particle breakage rates in wet batch ball milling[J]. Powder Technology, 2002, 124(1): 67−75.

[19] YEKELER M, OZKAN A, AUSTIN L G. Kinetics of fine wet grinding in a laboratory ball mill[J]. Powder Technology, 2001, 114(1/3): 224−228.

[20] 田金星. 石墨及其混合物料的磨碎动力学行为[J]. 中国有色金属学报, 1996, 6(4): 47−50. TIAN Jing-xing. The grinding kinetic behaviors of graphite and its mixture[J]. The Chinese Journal of Nonferrous Metals, 1996, 6(4): 47−50.

[21] 田金星, 谭旭升. 混合物料中石墨组分的碎裂特性及参数估计[J]. 中国有色金属学报, 2014, 24(10): 2582−2587. TIAN Jing-xing, TAN Xu-sheng. Fracturing characteristic and parameter estimate of graphite component of mixture[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2582−2587.

[22] 刘开忠, 翁伟雄, 周忠尚. 混合物料组分的碎裂参数特性[J]. 中国有色金属学报, 1995, 5(2): 47−50. LIU Kai-zhong, WENG Wei-xiong, ZHOU Zhong-shang. The fracturing parameter characteristics of mixture components[J]. The Chinese Journal of Nonferrous Metals, 1995, 5(2): 47−50.

Ball grinding characteristic and breakage parameters of chlorite

ZHAO Rui-chao1, 2, HAN Yue-xin1, HE Ming-zhao3, LI Yan-jun1

(1. School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China; 2. School of Coal & Mining Engineering, Inner Mongolia University of Science & Technology, Baotou 014010, China; 3. CITIC Pacific Mining Management Pty Ltd., 45 St. Georges Terrace, Perth, WA6000, Australia)

Under an invariant mill environment, batch wet ball grinding studies were carried out by grinding four mono-sized fractions of single mineral of chlorite. The results show that all mono-sized fractions of chlorite follow the first-order breakage mechanism.The maximum breakage rate for chlorite, obtained in the feed size fraction of 0.25−0.5 mm, is 0.35 min−1. The normal breakage behavior is obtained when the feed size is less than 0.5 mm. The fine fraction output for 0.25−0.5 mm size fractions of chlorite has a clear the zero-order output characteristics at a relatively short grinding time. The cumulative breakage distribution functions for 0.25−0.5 mm size fractions of chlorite are obtained using-algorithm. The simulated product size distribution data obtained，using the discrete-size, continuous-time Population Balance Model (PBM), are consistent with experimental data for 0.25−0.5 mm size fractions of chlorite.

chlorite; wet ball grinding; population balance model; breakage rate; cumulative breakage distribution function

Project(2012BAB14B05) supported by the National Key Technology R & D Program of Ministry of Science & Technology of China; Project(N140108001) supported by the Major Scientific and Technological Innovation Projects of Fundamental Research Funds for the Central Universities, China; Project(2011NCL042) supported by the University Research Fund of Inner Mongolia University of Science & Technology, China

2017-02-24;

2017-09-20

HAN Yue-xin; Tel: +86-24-83680162; E-mail: dongdafulong@mail.neu.edu.cn

“十二五”国家科技支撑计划项目(2012BAB14B05)；中央高校基本科研业务费重大科技创新项目(N140108001)；内蒙古科技大学创新基金项目(2011NCL042)

2017-02-24；

2017-09-20

韩跃新，教授，博士；电话：024-8368 0162；E-mail：dongdafulong@mail.neu.edu.cn

10.19476/j.ysxb.1004.0609.2018.05.25

1004-0609(2018)-05-1076-07

TD913

A

(编辑 王 超)