城市轨道交通PPP项目政府补贴调整模型研究

陶俐言，唐瑞坤

（杭州电子科技大学 管理学院，浙江 杭州 310018）

一、引言

PPP（Public-Private Partnership）是政府为提供某种公共服务，吸引社会资本的加入，给予私人组织在合作项目的一定特许权，并且签署相关合同明确双方的责任和权利，使合作双方形成一种伙伴关系，达到双赢。城市轨道交通可以有效缓解交通堵塞的压力，也使得城市空间更有效合理利用，因此得到政府和公众的广泛认同。在城市轨道交通项目中应用PPP模式，可以鼓励社会资本参与到项目中来，降低政府财政压力。目前我国PPP项目补贴模式[1]主要有建设期补偿模式（SB-O-T）和运营期补偿模式（B-SO-T）。

针对城市轨道交通PPP项目的政府补贴额问题，相关的文献主要从激励性补贴和外部效益补贴两方面研究。激励性补贴研究方向，徐丹、简迎辉和郑胜强[2]分析识别城市轨道项目中亏损的类型，在确定政府补贴基数的基础上，设计一种激励机制作为补贴额的参考，形成新的轨道交通补贴机制；赵源、欧国立[3]以三种投资融资模式对应的补贴模式为基础，分析不同的模式在运营的各个阶段的成本，提出补贴模型，以期提高企业效率；刘林和石世英[4]在分析合作双方信息存在不对称情形下政府的补贴额问题的基础上，提出不同阶段分别对应不同的激励性补贴模式的思路。在外部效益补贴方面，张智慧和张剑寒[5]探讨开发城市轨道交通项目产生的外部效益与政府补贴之间的关系，采用适当的方法测算出项目的外部效益之和，作为政府补贴的参考指标；朱成爱[6]对城市轨道项目的外部性综合分析，给政府补贴的调整提出了不同建议；申燕[7]通过分析上海市轨道交通的外部效益，并对主要利益相关方造成的影响分析，对我国城市轨道交通的政府补贴的确定有一定的参考意义；佟琼和张晶[8]通过分析轨道交通外部性，总结了影响项目外部性的指标体系，建立计算项目外部性的模型，与实际政府补贴比较，给出了一些有用的建议。

本文在已有的科研成果的基础上，构建政府补贴调整模型，并增加公众满意度作为政府补贴的参考指标，为政府补贴提供参考方向。

二、城市轨道交通PPP项目政府补贴调整分析

假设TC为项目的特许经营期，TC由建设期Tb和运营期To构成，NPV是项目运营企业在特许经营期内的收益净现值，CIt和COt分别是项目从建设期开始第t年的现金流入和现金流出，Wt为第t年政府给予项目运营企业的补贴，W0是财政补贴基数，t为城市轨道交通运营企业的投入（资金投入，服务水平等），f（s）为企业在 s水平的投入下公众满意度，i为行业基准折现率。

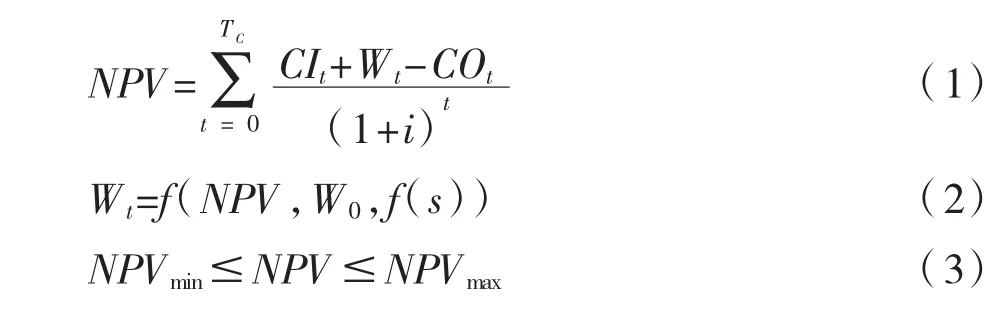
公式（1）表示在当前的基准折现率下，增加了政府补贴额时的企业收益净现值。公式（2）是政府补贴额，综合考虑企业的收益净现值NPV和政府补贴基数W0以及公众满意度f（s）。公式（3）表示政府与企业协商的双方可接受的NPV下限和上限。

本研究主要以NPV作为衡量项目运营企业的收益水平指标。NPV曲线可能发生的变动如图1所示。NPVmax（t）为项目的净现值NPV达到协商的净现值上限时的预期曲线，NPVmin（t）为项目的NPV取得协商的净现值下限时的预期曲线。

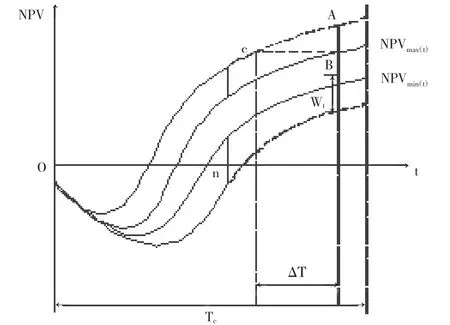
图1 政府补贴调整分析

城市轨道交通项目经过n年后，拥有了n年的运营数据，通过适当的方法，并结合前n年的客流量、成本等数据，可以模拟预测特许期之后每年的净现值NPV（图1中虚线部分即为预测的数据）。由于第 n年后预测得出的 NPV可能在[NPVmin（t），NPVmax（t）]之间上下波动，可能情况会有图 1 中的三种情况。第一种，NPV＞NPVmax（t）第 n 年末测算出项目的净现值超过约定的净现值上限，则应当降低票价或缩短特许经营期以防止项目运营企业通过垄断牟取暴利。若通过降低票价使NPV回归合理水平，需要考虑年客流量、运营成本的因素，若通过缩短特许经营期使 NPV回到[NPVmin（t），NPVmax（t）]之间，则由图 1 可知，首先由 A 点下降至B点，再从B点水平移到C点所得到的ΔΤ即应该缩短的特许经营期。第二种，NPV在[NPVmin（t），NPVmax（t）]之间，这种情况是净现值收益合理的情况，政府不须进行补贴。第三种，NPV在 NPVmin（t）之下，即项目NPV低于项目企业所能接受的净现值下限，政府应当给予项目运营企业适当的补贴。

三、城市轨道PPP项目补贴调整模型

（一）模型假设

在建立模型之前需要进行以下假设：（1）假设项目能在预定的时间内完成，暂时不考虑项目完工风险；（2）使用蒙特卡罗方法模拟项目运营期的净现值所使用的折现率不变；（3）如果当年的客流量低于预期而导致收益减少，政府部门能在该年约定时间对运营企业给予补贴。

（二）特许期调整模型

政府为避免运营企业收益比预期高，降低自身风险，可以适当缩短项目特许期。根据前n年的运营数据，预测TC-n年每年的净现值数据，当预测的净现值NPV比NPVmax大时，政府将缩短运营企业的特许经营期，其决策函数为：

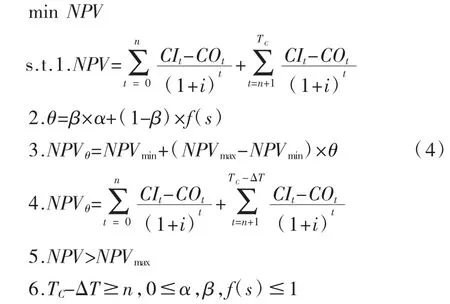
在公式（4）中，目标函数是在调整运营企业特许期后，净现值NPV最小。条件1是根据前n年的数据，测算出项目在特许期结束后的收益净现值NPV。条件2确定政府补贴系数θ，其中α是政府基础的补贴系数，f（s）是公众满意度，可以通过公众出行评价、服务评价等做定性分析，对企业的运营效率和项目的外部效益等指标做定量分析，综合以确定公众满意度。β是权重系数，以确定政府基础的补贴系数α和公众满意度f（s）在确定补贴系数θ各自所占的权重[2]。条件3是经过调整后的收益净现值。条件4是通过调整后的收益净现值计算出应该减少的经营期ΔT。条件5是触发条件，即当测算收益净现值大于商定的收益净现值上限时进行调整。条件6调整函数有效性约束，进行调整时尽可能提前，以预留足够的经营期年限进行调整。

（三）政府补贴调整模型

在项目运营阶段，可能会发生因为同性质产品的竞争，如公交车、出租车等的竞争而导致需求量减少，政府政策变化导致运营状况不佳的情况。这种情况需要政府补贴使项目能正常运行，实现合作双方协定的目标。若测算出的NPV在NPVmin（t）之下，为了城市轨道项目能正常运行，给予运营企业一定的补贴，其调整模型如下：

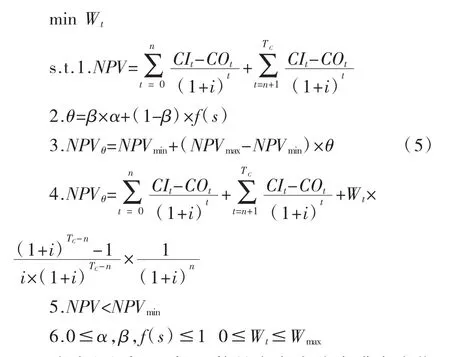
公式（5）中，目标函数是在考虑公众满意度指标后，使得政府每年的补贴额度Wt最小，激励运营企业同时，尽可能降低政府的财政风险。条件1、条件2和条件3含义与公式（4）相同。条件4是通过调整后的NPVθ计算出政府每年的补贴额Wt。条件5是政府补贴调整触发条件，即当项目净现值收益比协商的最低收益净现值低时，需要政府给予运营企业相应的补贴。条件6是调整模型有效性约束，Wmax是政府每年财政补贴上限。

（四）政府补贴调整思路

根据项目净现值情况，调整思路如图2所示。

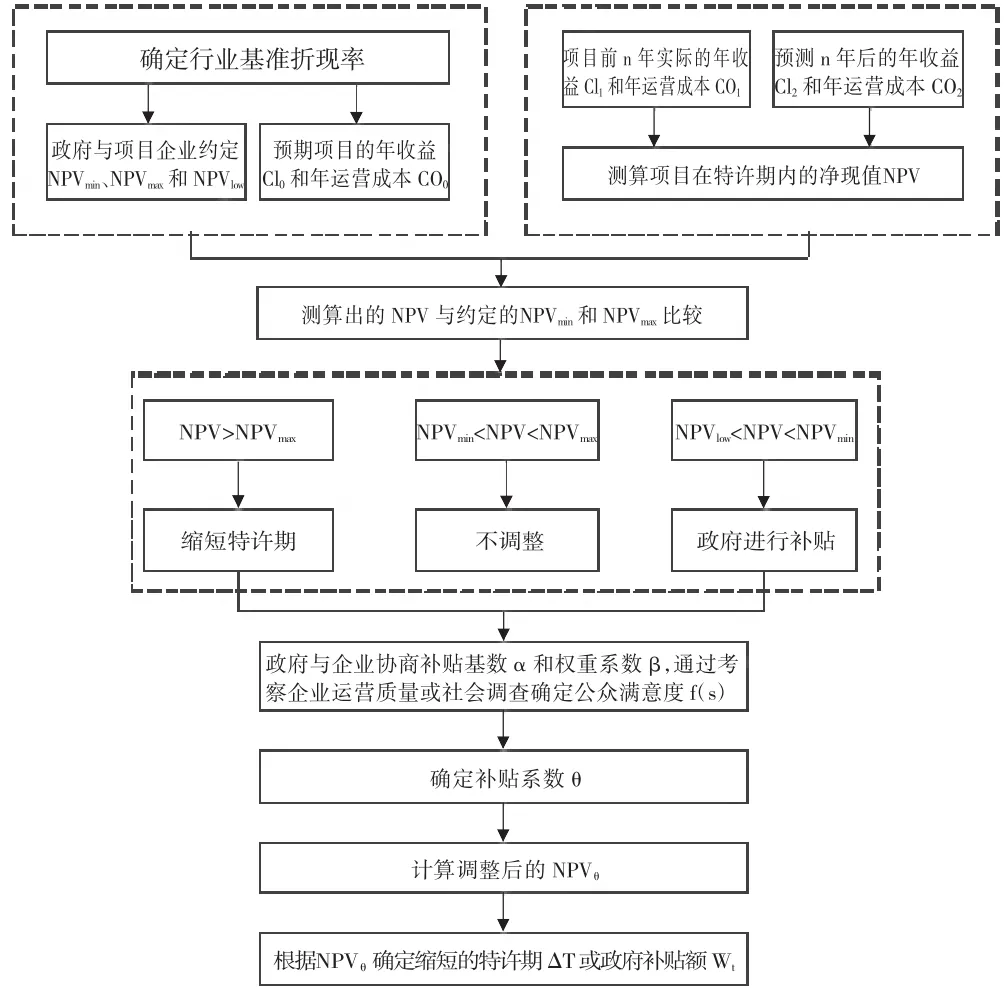
图2 政府补贴调整决策思路

四、案例分析

（一）案例背景

杭州地铁一号线采用PPP模式，引进香港铁路公司实施特许经营。杭州地铁1号线在2012年11月24日开始试运营，1号线工程投资主要分为A和B两部分。杭州地铁集团负责A部分，杭港地铁公司负责B部分，即B部分主要由社会资本投资，投资额为82.9亿元。双方约定，杭港地铁公司拥有25年的特许经营期，在经营期内，杭港地铁公司对杭州地铁1号线的资产进行运营和维护，在结束后交还给政府。在本案例分析中，基准折现率为10%，杭州地铁集团与杭港地铁公司协商的项目收益率最高为20%，最低为10%。

（二）NPV模拟分析

根据杭州地铁1号线运营数据，得到已运营年份的净现值，如表1所示。

依据北京联合资信评估有限公司公布杭港地铁公司的运营数据，对未来20年的年客流量、票价、运营单位成本、地铁沿线土地整合收入的概率分布进行预测，结果如表2所示。

表1 杭州地铁1号线前五年实际净现值

表2 关键参数的概率分布

应用CRYSTAL BALL 11.1.2.2软件对杭州地铁1号线运营期第5年后的净现值进行蒙特卡罗模拟，模拟次数设定为10 000次。依据表2的关键参数以及（6）式，可以模拟预测得到项目在第t年的 NPV，记为 NPVp|T0＝t（6≤t≤25），公式（6）中的NPVp|T0＝5为第5年末的NPV。使用蒙特卡罗方法模拟得到在之后每年的NPV，如表3所示。

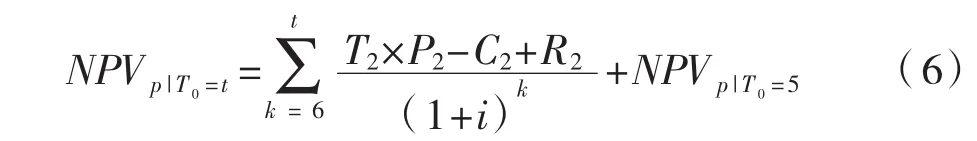
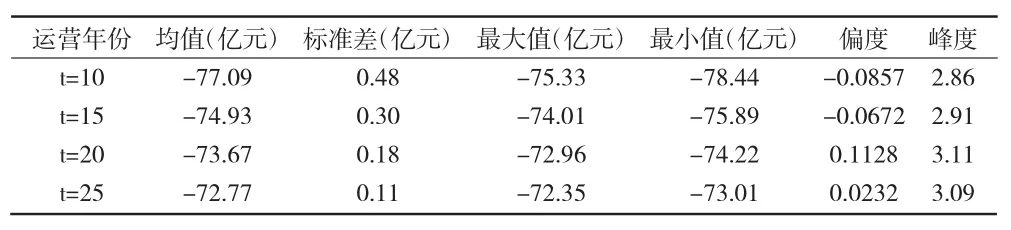
表3 项目运营5年后的净现值模拟结果

（三）政府补贴的调整

表3数据表明，在特许期结束后的收益为-72.77亿元，与约定的10%投资回报率有很大的差距。因此，本案例属于第三种情况，即NPV在NPVmin（t）之下，为了鼓励企业的积极性，避免项目失败，政府需要向企业给予适当的补贴。分析如下：

1.计算调整之后的NPVθ。在本案例中，为了提高社会资本的积极性并且降低政府的财政压力，双方商定的补贴基数β为0.01，社会满意度f（s）为0.05，权重比例为4∶6，根据公式（5）的条件 2和条件3计算调整后的NPVθ：

θ=0.4×0.01+0.6×0.05=0.034

NPVθ=82.9×10%+82.9×（20%-10%）×0.034=8.3182亿元

2.计算调整后政府每年应给予的补贴额Wt。根据公式（5）条件4计算补贴金额Wt：

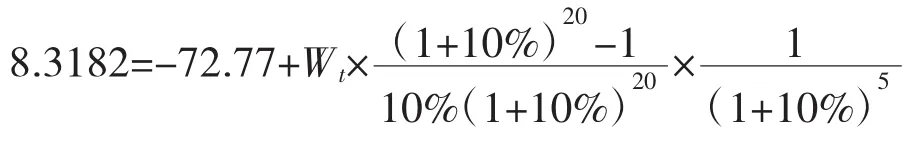
计算可得Wt=15.33亿元，即为了满足双方协商的最低10%回报率以及激励回报，政府需要在剩下的20年特许期内每年给予15.33亿元的补贴。

（四）结果分析

为了更好地表示杭港地铁公司在接受政府的15.33亿元补贴额后的项目收益净现值，对杭州地铁1号线第25年的收益净现值的分析，通过蒙特卡罗方法经过10 000次的测试，拟合净现值的分布函数。

表4 概率分布拟合比较

图3 NPVt=25频率分布图

由图3可知，项目在 N PVt＝25的期望值为8.25亿元，偏度为-0.000 4，峰度为2.96。对净现值的分布进行拟合，根据表4可知最优拟合分布是对数正态分布Lognormal，因此，近似地认为净现值NPVt＝25近似服从对数正态分布 L ognormal（8.25，0.11）。

使用散点图分析净现值与各个变量之间的关系。图4、图5和图6与净现值呈正相关的关系，应努力提高。图7与净现值呈负相关的关系，应努力降低。

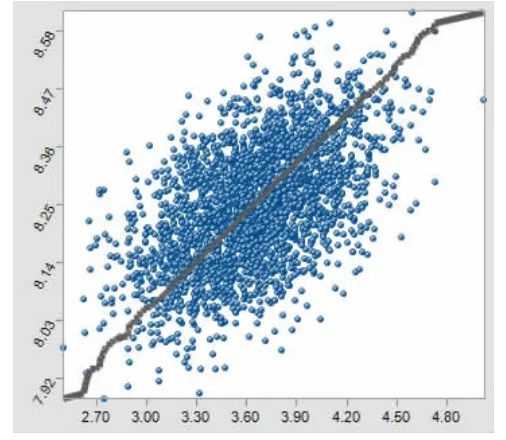
图4 票价收入散点图

图5 年客流量散点图

图6 沿线土地整合收入散点图

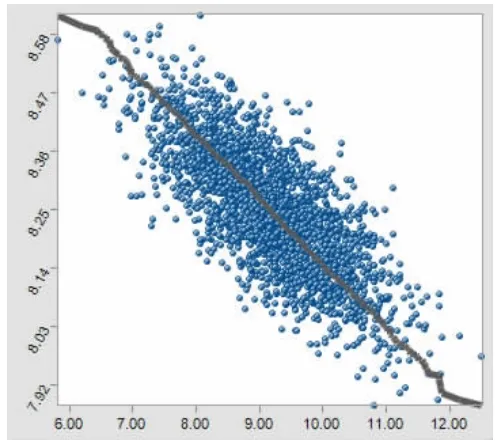
图7 运营成本散点图

最后，在折现率为10%时测算净现值的累积概率，如图8所示。

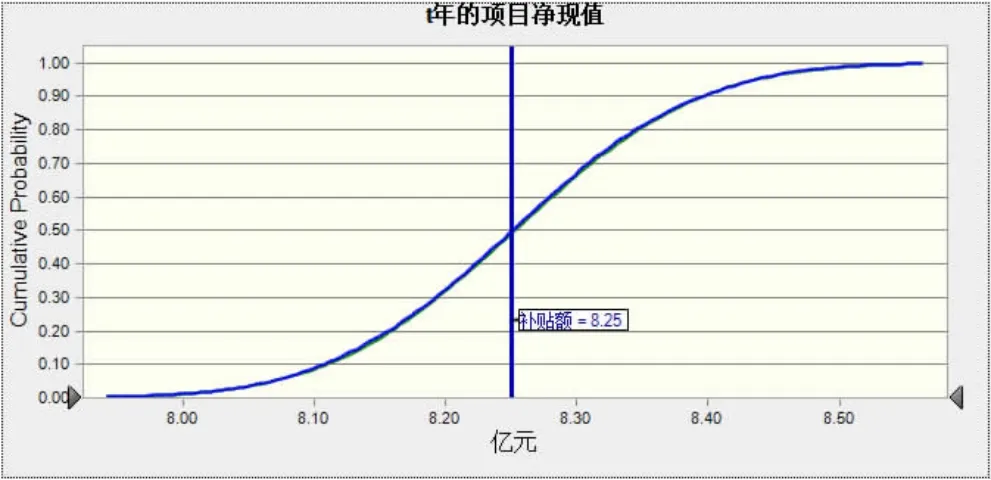
图8 当折现率为10%时的累积概率曲线

获得政府的补贴后，净现值的累积概率为50%，符合Thomas、Xie和Cheung等学者提出的在[30%，80%]区间的标准[9]。因此政府对项目运营企业补贴相应的补贴额可以使项目能正常运营，同时也保证了项目运营企业能获得预期的收益。

五、结论

根据城市轨道交通项目所属的政府部门的财政分配情况和实际PPP项目运营情况，风险分担的方式一般可以有以下几种：

第一，若项目运营期间，因政府部门的票价政策而导致项目运营企业的亏损，政府可以给予项目运营企业补贴而使得地铁项目正常运行，本案例采取的风险分担方式属于此类。

第二，若项目在运营期间盈利，但是预计在特许期内不足以达到合作双方约定的收益额度，若项目所属政府一般公共支出预算支持进行相应的补贴，则进行适当的补贴。若财政预算力不允许进行相应的补贴，则可以延长项目运营企业的特许经营期，计算方法可参考特许期调整模型。若政府为了能尽快回收项目控制权，可以同时采取补贴和特许期调整这两种方式。

第三，若项目在运营期间盈利，预计在特许期内项目运营企业获得的收益将会超过双方约定的收益额度。在可以使用特许期调整模型适当缩短项目运营企业的特许经营期，在项目正常运行的条件下，政府部门尽快收回项目控制权。

风险分担方式的选择不仅要考虑当地政府财政承受能力，也需要根据项目实际运营情况选择调整特许期或者进行补贴，使政府财政压力尽可能小。因此在选择风险分担方式时，要综合考虑这两种因素，使得双方共赢情况下，政府部门能尽可能少地支出补贴额，尽可能快地回收项目控制权。

后续研究可以考虑多因素协同调整，比如考虑票价与特许期的联动调整，进一步研究建立票价补贴的动态调整机制，并且结合我国PPP项目实践深入探讨上述理论的应用。

[1]向鹏成，蒋飞.基于风险分担的城市轨道PPP项目收益补贴调整模型[J].建筑经济，2016，37（2）：45-50.

[2]徐丹，简迎辉，郑胜强.PPP模式下城市轨道交通的补贴机制研究[J].项目管理技术，2013，11（10）：76-80.

[3]赵源，欧国立.城市轨道交通补贴机制研究[J].北京交通大学学报（社会科学版），2008，7（2）：7-11.

[4]刘林，石世英.城市基础设施PPP项目政府补贴方式研究[J].项目管理技术，2016，14（4）：7-12.

[5]张智慧，张剑寒.城市轨道交通PPP项目运营补贴测算[J].清华大学学报（自然科学版），2016，56（12）：1327-1332.

[6]朱成爱.我国城市综合交通枢纽运营单位外部利益返还机制研究[J].建筑经济，2011，s1（34）：13-16.

[7]申燕，2013.优化上海市轨道交通票价的基本思路[J].价格理论与实践（7）：54-55.

[8]佟琼，张晶.基于外部效应的北京城市轨道交通补贴额度研究[J].北京交通大学学报（社会科学版），2011，10（2）：40-46.

[9]Thomas S N，Xie J Z，Cheung Y K，et al.A simulation model for optimizing the concession period of public private partnerships schemes[J].International Journal of Project Management，2007，25（8）：791-798.