循环流化床锅炉燃烧系统的神经网络模型研究

李国强， 齐晓宾， 陈 彬， 张 露

(燕山大学 河北省工业计算机控制工程重点实验室，河北秦皇岛 066004)

热电厂锅炉燃烧系统产生的氮氧化物(主要是NO和NO2，统称NOx)是大气的主要污染源之一[1-2]。准确预测NOx的排放特性对于调整系统输入量、减少NOx排放量和改善大气质量有着至关重要的作用。然而，影响锅炉NOx排放量的因素很多，且锅炉的燃烧过程具有强耦合和非线性等特征，很难用机理模型去描述。近些年，神经网络广泛应用于解决工程领域中的建模与控制问题，但传统神经网络训练模型需经多次迭代调整才能确定网络权值[3]，存在计算时间长和易陷入“过拟合”的缺点[4]。

2003年，Caminhas等[5]提出了一种新的网络，称为并行层感知器(Parallel Layer Perceptron, PLP)，利用并行的感知器来映射输入层与输出层之间的非线性关系。PLP试图结合多层感知器(multi-layer perceptrons, MLP)[6-7]和基于自适应神经网络的模糊推理系统(adaptive-network-based fuzzy inference system, ANFIS)的优点[8]，该模型已被广泛应用[9-12]，相关文献已对PLP做出详细介绍[5]。2006年，黄广斌等[13]提出一种性能出色的单隐层前馈神经网络，称为极限学习机(Extreme Learning Machine，ELM)。ELM的模型和理论[14-15]被成功应用于函数逼近[16-17]、模式分类[18]和系统辨识等许多领域。ELM的核心内容是将单隐层模糊神经网络转化为求解线性最小二乘问题，然后通过Moore Penrose(MP)广义逆计算输出权值。2013年，Li等[19]提出了一种基于ELM的新型人工神经网络——快速学习网(Fast Learning Network, FLN)。FLN在继承了ELM优点(网络结构简单，回归精度、泛化能力强，收敛速度快，无需迭代)的同时，输出神经元不仅接收来自隐层单元的信息，而且还接收来自输入层单元的信息，对于线性与非线性问题的处理能力更强。

笔者提出了一种新型的神经网络结构——并联型快速学习网(Fast Learning Network with Parallel Layer Perceptron, PLP-FLN)。这是1个单层前馈神经网络和2个单隐层前馈神经网络并行连接结构。因此，PLP-FLN也具有处理线性和非线性问题的优势，可以被视为FLN与PLP网络的结合模型。若不考虑线性连接，PLP-FLN还可以被看做以ELM为基本框架的并联型感知神经网络。因此，PLP-FLN也继承了ELM泛化能力好、学习速度快、模型复杂度低等优点。笔者将PLP-FLN与ELM、FLN、IELM、KELM模型的预测结果进行了对比研究，实验证明PLP-FLN具有更好的拟合能力，为预测电厂锅炉NOx排放提供了一种新的有效参考。

1 快速学习网模型

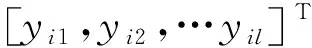
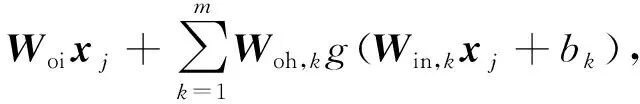
j=1,2,…,N

(1)

式中：Woi=Woi,1,Woi,2,…,Woi,l，为连接输入层与第j个输出节点之间的权值矩阵；Woh,k=[Woh,1k,Woh,2k,…,Woh,lk]T，为连接第k个隐层节点与输出层之间的权值矩阵；Win,k=[Win,k1,Win,k2,…,Win,km]T，为输入层与第k个隐层节点之间的权值矩阵；bk为第k个隐层节点的阈值。

式(1)可表达成矩阵形式为：

(2)

(3)

(4)

式中：W为输出权值矩阵；G为隐层输出矩阵；Y为期望输出矩阵；l为输出层节点个数。

根据最小二乘范数解的相关知识，输出权值矩阵W的最小二乘范数解为：

(5)

(6)

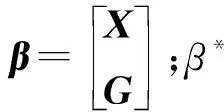
2 并联型快速学习网

2.1 PLP-FLN网络模型

PLP-FLN可以看成是并联型感知器与快速学习网的结合模型，其中输入层将接收到的数据信息传送给2个并联的单隐层前馈网络和输出层，这样的结构具有以下特点：1)隐层神经元接收样本信息并进行非线性处理后传递给输出层，PLP-FLN并联的单隐层前馈网络结构增强了自身的非线性处理能力；2)输入层直接将样本信息传递给输出层，增加了网络对数据的线性处理能力。PLP-FLN结构如图1所示，其学习过程呈现如下：

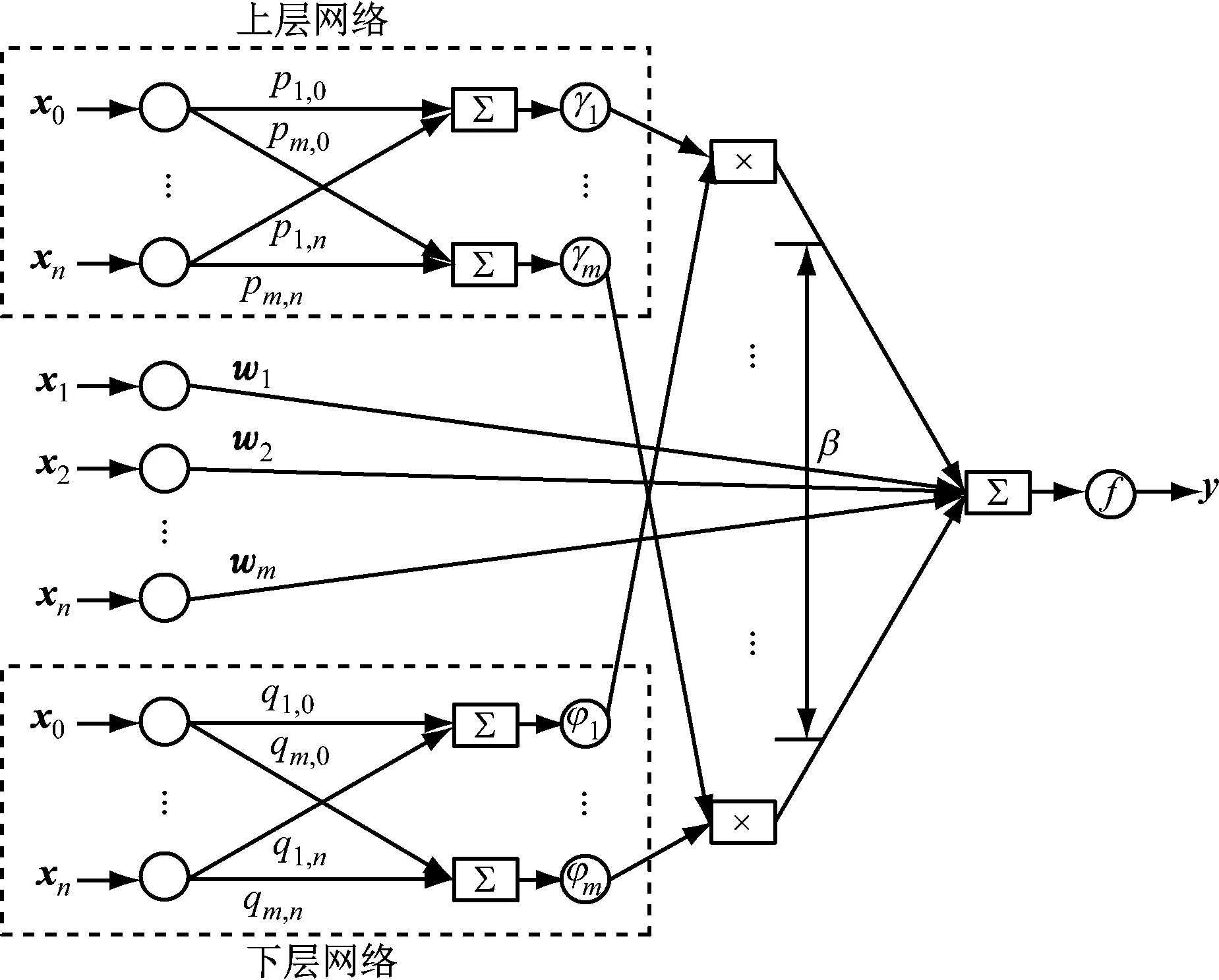
图1 PLP-FLN结构图

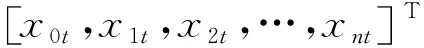
(7)

式中：f(·)、γ(·)和φ(·)均是激活函数。

ajt、bjt和ckt分别表示如下：

(8)

(9)

(10)

式中：pjt、qjt和wkt为不同层的权值矩阵元素。

与传统的单隐层前馈神经网络(single layer feedforward neural network，SLFN)一样，PLP-FLN所有的权值可在训练阶段进行调整。

上层网络的隐层输出可表示为：

(11)

下层网络的隐层输出可表示为：

(12)

式(11)可以被写成如下数学模型：

gt=γ(Pxt)，t=1,2,…,N

(13)

式中：P=[P1,P2,…,Pm]，为上层网络连接第j个隐层节点与输入层节点的权值向量。

同样，式(12)可写成：

(14)

式中：Q=[Q1,Q2,…,Qm]，为下层网络连接第j个隐层节点与输入层节点的权值向量。

式(13)和式(14)可用矩阵形式表达为：

G1=γ(PX)

(15)

G2=φ(QX)

(16)

式中：X为包含隐层阈值x0的输入样本矩阵。

通过位相乘运算后可以得到新矩阵：

(17)

式中：G为PLP-FLN的隐层输出矩阵。

(18)

式中：H为输出层的输入矩阵；X1为不包含隐层阈值x0的输入样本矩阵。因此，神经网络最后的输出可以写成矩阵形式：

T=f(Hβ)

(19)

式中：T为期望的输出矩阵；β为PLP-FLN的输出权值矩阵。

单隐层前馈神经网络的输入权值和隐层阈值不必完全调整，可以被初始化到一个随机数。因此，PLP-FLN的输入权值P、Q和隐层阈值x0被随机初始化到(0,1)之间的数，从而将求取输出权值β转化成最优化问题，如式(20)所示：

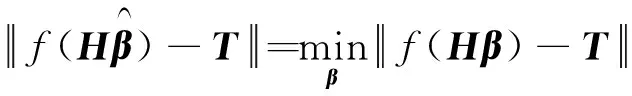
(20)

对于可逆的激活函数f(·)，上式可转化为线性最小化问题，输出权值可由下式解析得到。

(21)

式中：f-1(T)为激活函数f(·)的逆函数。

根据Moore-Penrose(MP)广义逆相关知识，上式中输出权值的最小二乘范数解可写成：

(22)

式中：H+为矩阵H的广义逆。

2.2 PLP-FLN简化模型

作为式(1)的特殊情况，假设激活函数γ(·)和f(·)是线性函数，则网络的输出可写成：

(23)

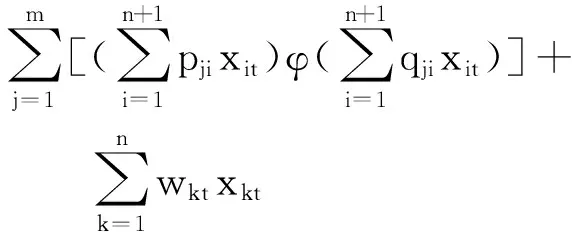
(24)

简化的网络模型具有一些好的特性。在随机初始化输入权值和隐层阈值的情况下，可以用最小二乘法求得网络的输出权值。若能够通过有效的方法求得合适的隐层节点个数，则PLP-FLN可以表现出快速的学习速度、优秀的泛化能力和学习能力等。

3 PLP-FLN性能测试

运用3折交叉验证法(cross validation, CV)获得不同模型在各数据集下的最优隐层节点个数，再用网格法(Grid Search, GS)获取核极限学习机的参数组合C(惩罚系数)和γ(核参数)，其网格分别设置为C=[2-4,2-3,…,214,215]和γ=[2-4,2-3,…,214,215]，每次实验从400个参数组合中找出最优的组合作为KELM的性能参数。为了验证PLP-FLN模型的有效性，进行了基准回归实验。隐层激励函数均采用‘sig’函数。针对每个回归问题,均重复实验30次，并将测试样本的实验结果与ELM、 FLN、KELM和IELM的测试结果进行了对比。

使用8个UCI数据集(http://archive.ics.uci.edu/ml/datasets.html)进行回归实验，数据集的输入属性和输出属性分别归一化到[-1,1]和[0,1]。数据相关信息如表1所示。

表1 基准回归数据

表2给出了不同网络最优隐层节点个数和KELM参数的确定。由表2可知，在达到实验最高精度的情况下ELM、FLN和IELM所需要的隐层节点个数远多于PLP-FLN所需的隐层节点个数，有的甚至多十几倍。总体看来，PLP-FLN的隐层节点个数保持在10以内。结合下文的实验结果可知，PLP-FLN在设置较少隐层节点个数的情况下，能获得与其他4种模型相同或较好的实验结果，展现了较好的数据处理能力。

表2不同网络最优隐层节点个数和KELM参数的确定

Tab.2Optimalnumberofhiddenlayernodesfordifferentalgorithmsandthehyper-parametersofKELM

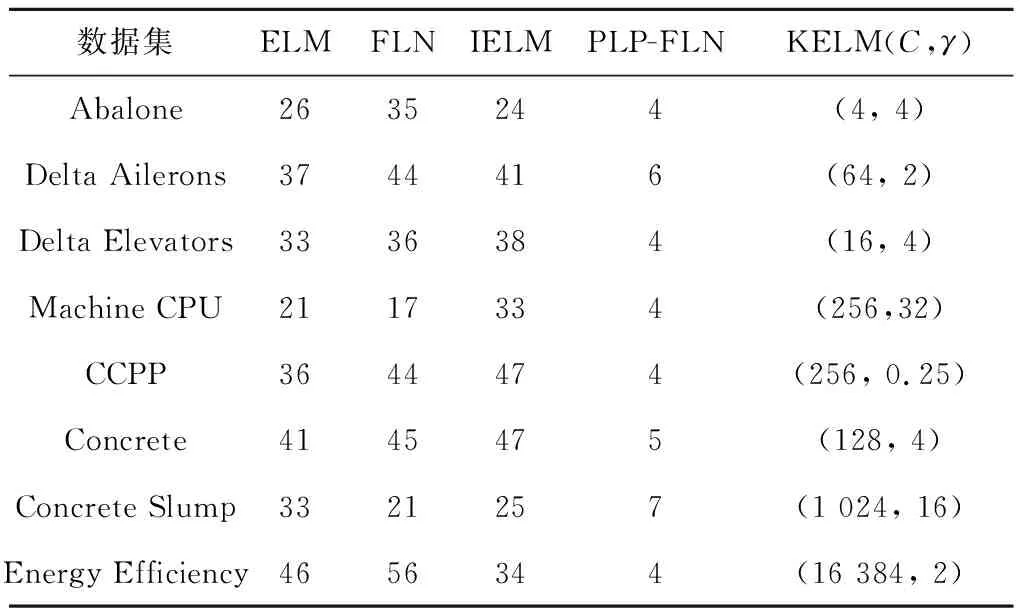
数据集ELMFLNIELMPLP-FLNKELM(C,γ)Abalone2635244(4, 4)Delta Ailerons3744416(64, 2)Delta Elevators3336384(16, 4)Machine CPU2117334(256,32)CCPP3644474(256, 0.25)Concrete4145475(128, 4)Concrete Slump3321257(1 024, 16)Energy Efficiency4656344(16 384, 2)

由表3所示，引入均方根误差(Root Mean Square Error，RMSE)的标准差(Standard Deviation, SD)作为性能评价指标。在8个回归数据集中，ELM、 FLN、KELM和IELM分别只有2个、1个、3个和1个数据集的结果比PLP-FLN的结果好。对于数据集Delta Elevators和Concrete，PLP-FLN比其他4种模型都展现出更好的实验结果。总体来看，PLP-FLN在大部分数据集下的回归精度好于其他4种模型，PLP-FLN表现出较好的泛化能力、学习能力和稳定性。

如表4所示，引入相关系数(R-Square)和平均绝对百分误差(Mean Absolute Percentage Error，MAPE)作为性能评价指标。通过对比5种方法对于测试样本的测试结果，可以明显发现PLP-FLN在大部分数据集下的结果都优于其他4种模型，尤其是对于数据集Abalone、Delta Elevators、Concrete和Concrete Slump，PLP-FLN比其他方法展现出更小的MAPE值，对于数据集Abalone、Delta Ailerons、Machine CPU和Concrete Slump，PLP-FLN比其他方法获得更大的R-Square值，表明PLP-FLN较其他4种方法具有更好的预测能力和拟合度。

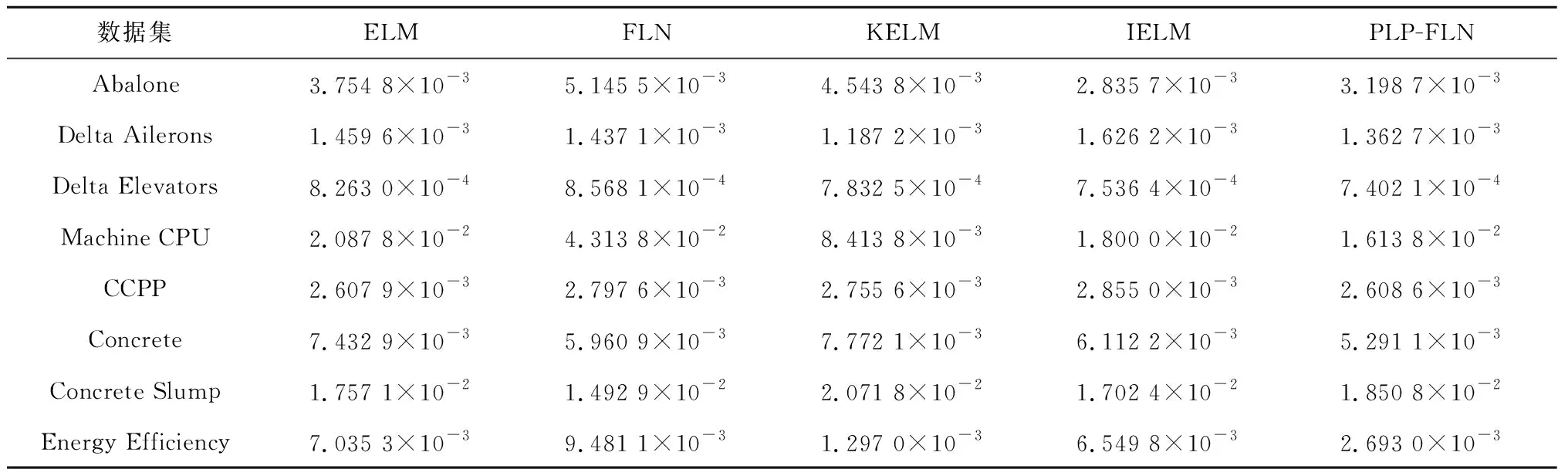
表3 5种方法测试样本均方根误差的标准差的比较

表4 测试样本平均绝对百分误差和相关系数的性能比较

4 循环流化床锅炉燃烧系统建模

以PLP-FLN建立模型，实验对象为某热电厂300 MW亚临界循环流化床锅炉。以集散控制系统(DCS)从热电厂数据库中采集的576组数据作为样本数据，将其随机分为训练样本(384组)和测试样本(192组)。数据负荷范围为60%～100%，由于一天当中各时间段发电量不同，实际负荷顺序并不是严格递增或递减的。选取NOx排放质量浓度作为模型的输出参数，影响NOx排放质量浓度特性的27个参数(负荷、给煤量、一次风流量、一次风温度、炉膛密相区温度等)作为模型的输入参数。

为了消除不同数据之间的量纲，加快网络收敛性，方便数据处理，先将样本进行归一化处理。输入参数归一化到[-1,1]，输出参数归一化到[0，1]，最后再将实验结果反归一化，这样处理更能反映出模型预测的真实效果。针对此数据，利用与上文同样的方法获得ELM、 FLN、IELM与PLP-FLN的最优隐层节点个数分别为46、32、54和10，KELM参数组合(C,γ)为(128,2)，其余实验参数和实验次数与上面设置相同。为了体现PLP-FLN模型的有效性，进行了与上面相同的4种模型的对比实验，并将均方根误差(RMSE)、标准差(SD)、平均绝对百分误差(MAPE，%)、平均绝对误差(Mean Absolute Error, MAE)和相关系数(R-square)作为实验结果的评价标准。

表5给出了测试样本准确度的对比。由表5可知，对于SD和MAE而言,8组实验数据中只有3种模型的实验数据比PLP-FLN的好，而对于RMSE、MAPE和R-square而言，PLP-FLN的实验结果分别为13.152 5、7.697 0%和0.914 9，比其他4种模型的实验结果都好。由此可知，PLP-FLN具有较好的泛化能力和预测能力。

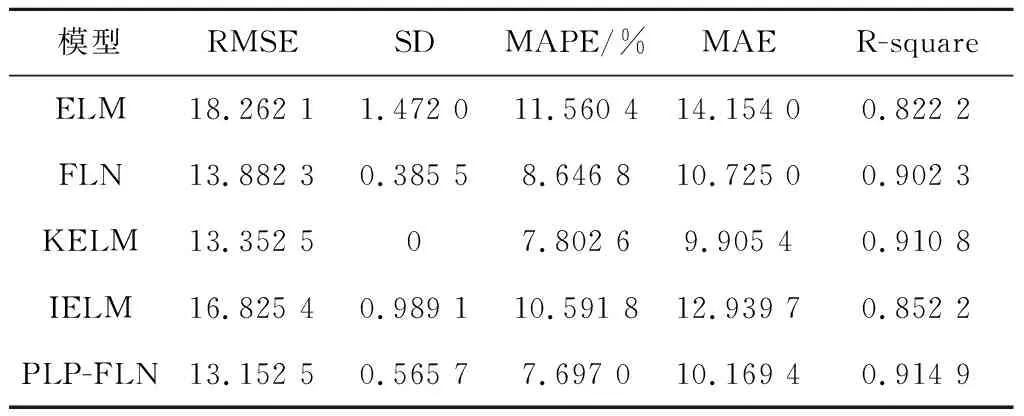
表5 测试样本准确度对比

为了更加清晰地展示PLP-FLN的实验性能，将5种方法的测试结果与NOx排放质量浓度的实际输出进行比较，结果如图2～图6所示。从拟合结果来看，PLP-FLN的预测值与目标值的拟合度最好，对于大多数差异较大的数值也能进行很好的拟合，表明其拥有较好的学习能力和预测能力。

各种模型对测试样本的预测误差如图7所示。由图7可以看出，与其他4种模型相比，PLP-FLN模型预测NOx排放质量浓度的误差范围最小，说明其预测结果更准确。

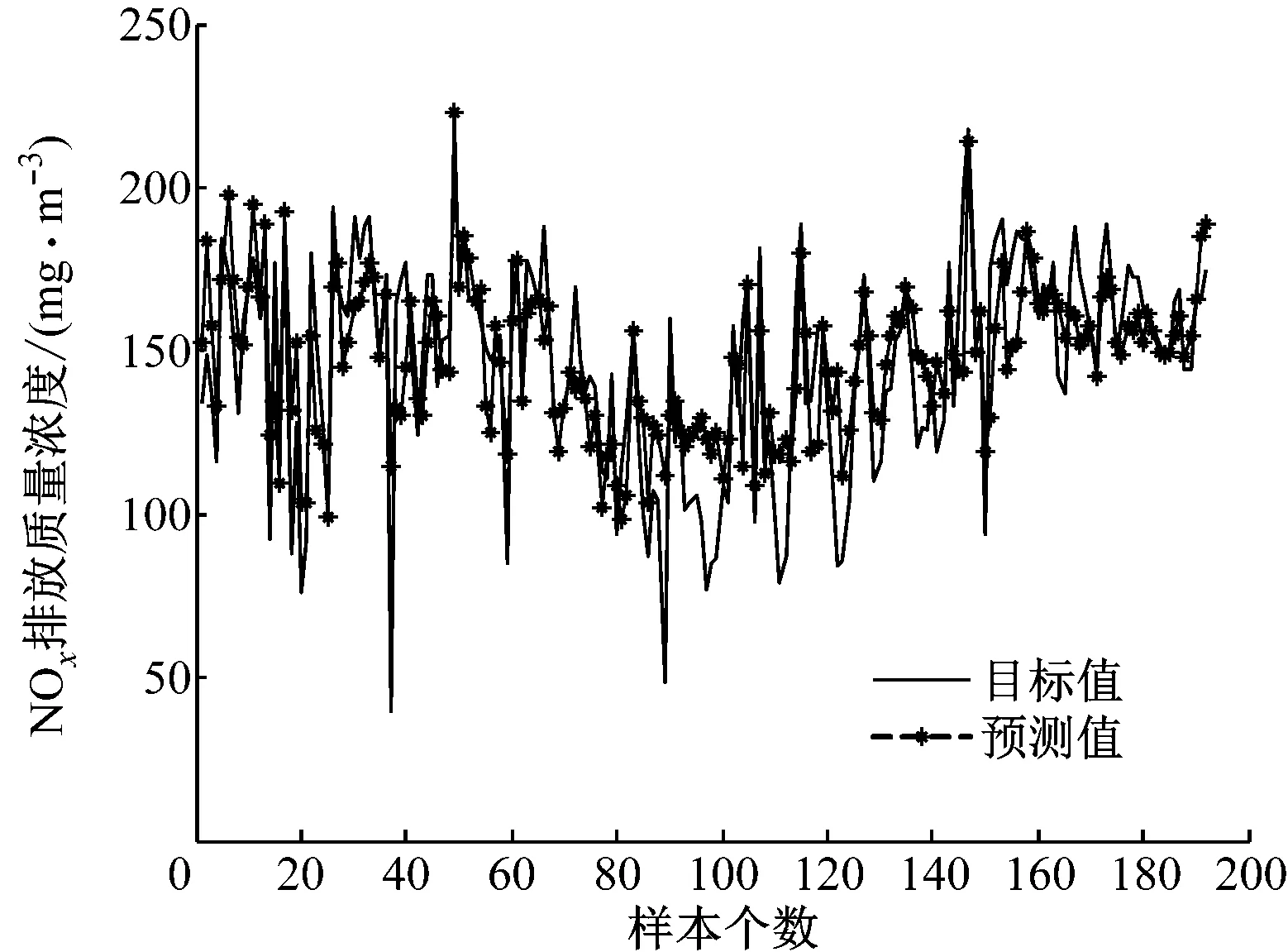
图2 ELM的预测值与目标值的对比

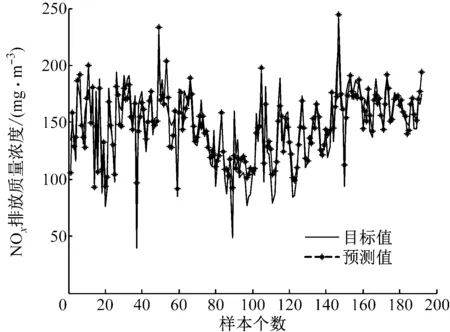
图3 FLN的预测值与目标值的对比

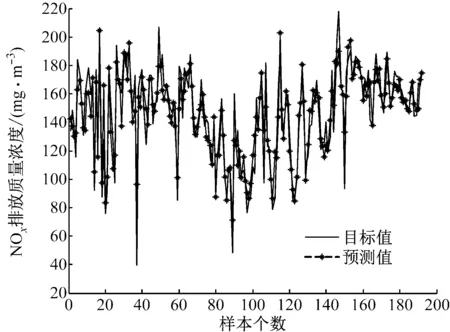
图4 KELM的预测值与目标值的对比

图5 IELM的预测值与目标值的对比

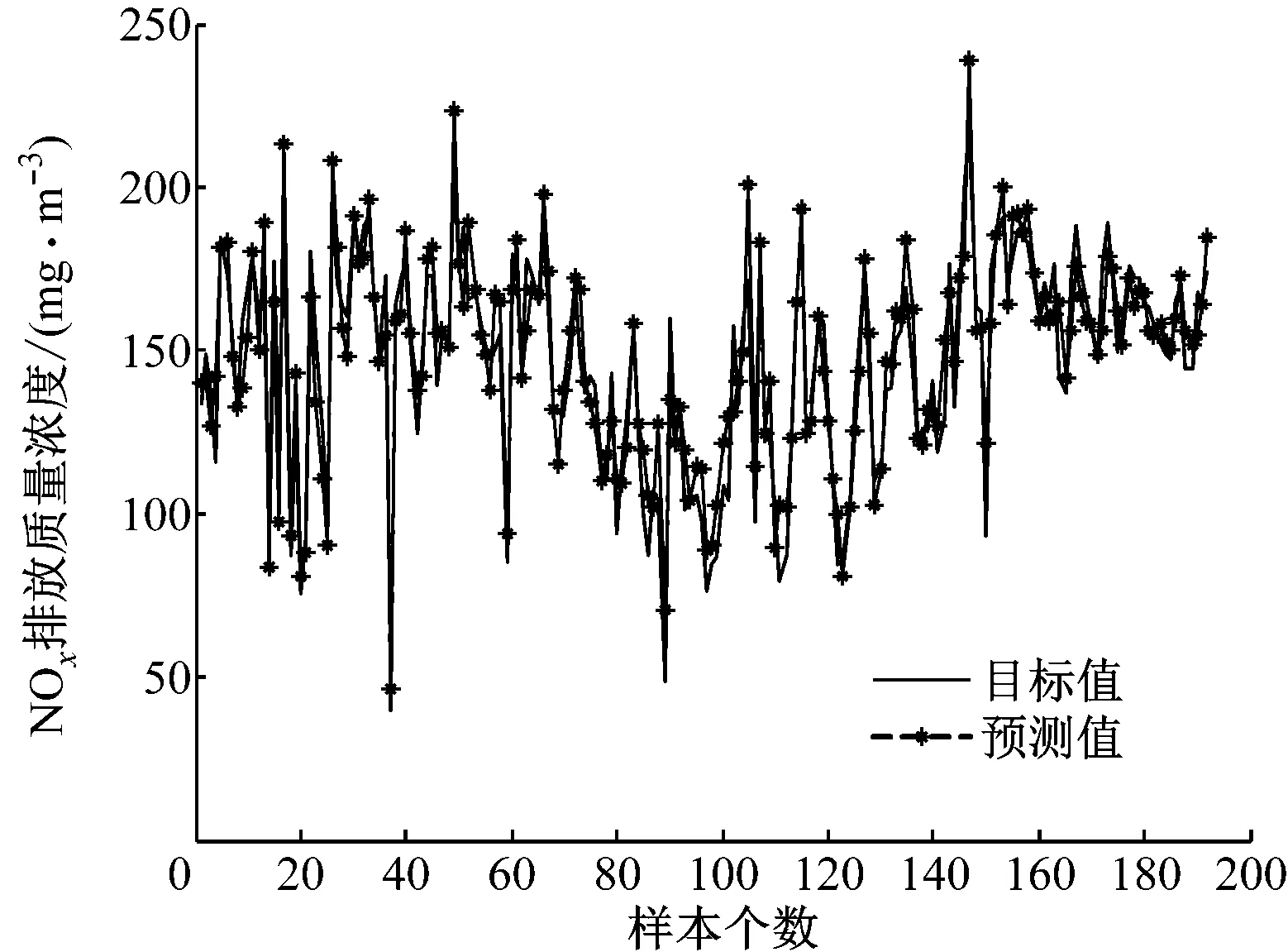
图6 PLP-FLN的预测值与目标值的对比

综上所述，通过实验对比可知笔者提出的PLP-FLN模型的学习能力和泛化能力更强，预测精度更高，非常适合循环流化床锅炉NOx排放质量浓度的预测。

5 结 论

以某热电厂300 MW亚临界循环流化床锅炉为研究对象，以现场采集的NOx排放质量浓度为模型输出样本，利用并联型快速学习网建立了循环流化床锅炉NOx排放质量浓度的预测模型，并将该模型的预测结果与ELM、FLN、KELM和IELM模型的预测结果进行了比较。结果表明：PLP-FLN模型可以更准确、有效地预测NOx排放质量浓度，为热电厂预测NOx排放质量浓度提供了一种新的方法。

参考文献：

[1] 欧阳子区, 朱建国, 吕清刚. 无烟煤粉经循环流化床预热后燃烧特性及NOx排放特性实验研究[J].中国电机工程学报, 2014, 34(11): 1748-1754.

OUYANG Ziqu, ZHU Jianguo, LÜ Qinggang. Experimental study on combustion and NOxemission of pulverized anthracite coal preheated by a circulating fluidized bed[J].ProceedingsoftheCSEE, 2014, 34(11): 1748-1754.

[2] 牛培峰, 赵振, 马云鹏, 等. 基于风驱动算法的锅炉NOx排放模型优化[J].动力工程学报, 2016, 36(9): 732-738.

NIU Peifeng, ZHAO Zhen, MA Yunpeng, et al. Model improvement for boiler NOxemission based on wind driven optimization algorithm[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(9): 732-738.

[3] 张弦, 王宏力. 限定记忆极端学习机及其应用[J].控制与决策, 2012, 27(8): 1206-1210.

ZHANG Xian, WANG Hongli. Fixed-memory extreme learning machine and its applications[J].ControlandDecision, 2012, 27(8): 1206-1210.

[4] 魏辉, 陆方, 罗永浩, 等. 燃煤锅炉高效、低NOx运行策略的研究[J].动力工程, 2008, 28(3): 361-366.

WEI Hui, LU Fang, LUO Yonghao, et al. Research on operation strategy on reducing NOxemissions and improving efficiency of coal-fired boiler[J].JournalofPowerEngineering, 2008, 28(3): 361-366.

[5] CAMINHAS W M, VIEIRA D A G, VASCONCELOS J A. Parallel layer perceptron[J].Neurocomputing, 2003, 55(3/4): 771-778.

[6] CULOTTA S, MESSINEO A, MESSINEO S. The application of different model of multi-layer perceptrons in the estimation of wind speed[J].AdvancedMaterialsResearch, 2012, 452-453: 690-694.

[7] ZHENG Lilei, DUFFNER S, IDRISSI K, et al. Siamese multi-layer perceptrons for dimensionality reduction and face identification[J].MultimediaTools&Applications, 2016, 75(9): 5055-5073.

[9] HUNTER D, WILAMOWSKI B. Parallel multi-layer neural network architecture with improved efficiency[C]//Proceedingsofthe4thInternationalConferenceonHumanSystemInteractions. Yokohama, Japan: IEEE, 2011: 299-304.

[10] GAO Zhenning. Parallel and distributed implementation of a multilayer perceptron neural network on a wireless sensor network[D]. Toledo, USA: The University of Toledo, 2013.

[11] LI Xiaojun, LI Li. IP core based hardware implementation of multi-layer perceptrons on FPGAs: a parallel approach[J].AdvancedMaterialsResearch, 2012, 433-440: 5647-5653.

[12] GARCIA-SALGADO B P, PONOMARYOV V I, ROBLES-GONZALEZ M A. Parallel multilayer perceptron neural network used for hyperspectral image classification[C]//Proceedingsof2016Real-TimeImageandVideoProcessing. Brussels, Belgium: SPIE, 2016: 98970K.

[13] HUANG Guangbin, ZHU Qinyu, SIEW C K. Extreme learning machine: theory and applications[J].Neurocomputing, 2006, 70(1/3): 489-501.

[14] DING Shifei, ZHAO Han, ZHANG Yanan, et al. Extreme learning machine: algorithm, theory and applications[J].ArtificialIntelligenceReview, 2015, 44(1): 103-115.

[15] JAVED K, GOURIVEAU R, ZERHOUNI N. SW-ELM: a summation wavelet extreme learning machine algorithm with a priori parameter initialization[J].Neurocomputing, 2014, 123: 299-307.

[16] DUDEK G. Extreme learning machine for function approximation-interval problem of input weights and biases[C]//Proceedingsofthe2ndInternationalConferenceonCybernetics. Gdynia, Poland: IEEE, 2015: 62-67.

[17] HUANG G B, SIEW C K. Extreme learning machine: RBF network case[C]//Proceedingsofthe8thControl,Automation,RoboticsandVisionConference. China: IEEE, 2012: 1029-1036.

[18] IOSIFIDIS A, TEFAS A, PITAS I. Dynamic action recognition based on dynemes and extreme learning machine[J].PatternRecognitionLetters, 2013, 34(15): 1890-1898.

[19] LI Guoqiang, NIU Peifeng, DUAN Xiaolong, et al. Fast learning network: a novel artificial neural network with a fast learning speed[J].NeuralComputingandApplications, 2014, 24(7/8): 1683-1695.