多支撑汽轮机轴承标高调整对轴封间隙的影响分析
2018-06-27顾家辉杨建刚朱溢铭
顾家辉, 冯 坤, 杨建刚, 朱溢铭
(1.东南大学 火电机组振动国家工程研究中心,南京 210096; 2.国家电投河南电力有限公司技术信息中心,郑州 450000)
大型汽轮发电机组轴系由高中压转子、低压转子和发电机转子等组成,轴系支撑数超过2个,是一个典型的静不定结构。轴承标高会影响轴承载荷分配,进而影响轴系的动力特性。轴承载荷过轻,轴系会失稳[1];轴承载荷过重,则会导致轴承瓦温升高、碾瓦等事故[2]。轴承标高变化在影响1x倍频振动的同时,也会对2x倍频振动分量产生较大影响[3]。因此,轴承标高调整是解决机组振动故障的有效手段[4-8]。
但是对于轴承标高的调整需慎重,轴承标高调整量大会改变动静部件之间的间隙,严重时会导致动静部件摩擦,甚至弯轴等恶性事故[9];轴承标高调整量小对机组振动的影响较小[10],甚至没有影响。受油膜、转轴弹性变形等因素的影响,轴封间隙变化量往往小于轴承标高调整量。
笔者基于轴承标高调整对轴封间隙的影响建立计算分析模型,研究不同状态下轴承标高对轴封间隙的影响,为解决机组振动问题提供了参考。
1 计算分析模型
轴承标高调整会引起轴承载荷变化,进而改变轴颈偏心距和偏位角。如图1所示,轴承标高抬升Δx后,轴颈实际升高量为:
Δh=ecosθ+Δx-e′cosθ′
(1)
式中:Δh为轴颈高度变化量;Δx为轴承标高调整量;e为初始偏心距;θ为初始偏位角;e′为轴承标高调整后的偏心距;θ′为轴承标高调整后的偏位角。e′和θ′与初始轴承标高、轴承标高调整量和轴承特性有关。
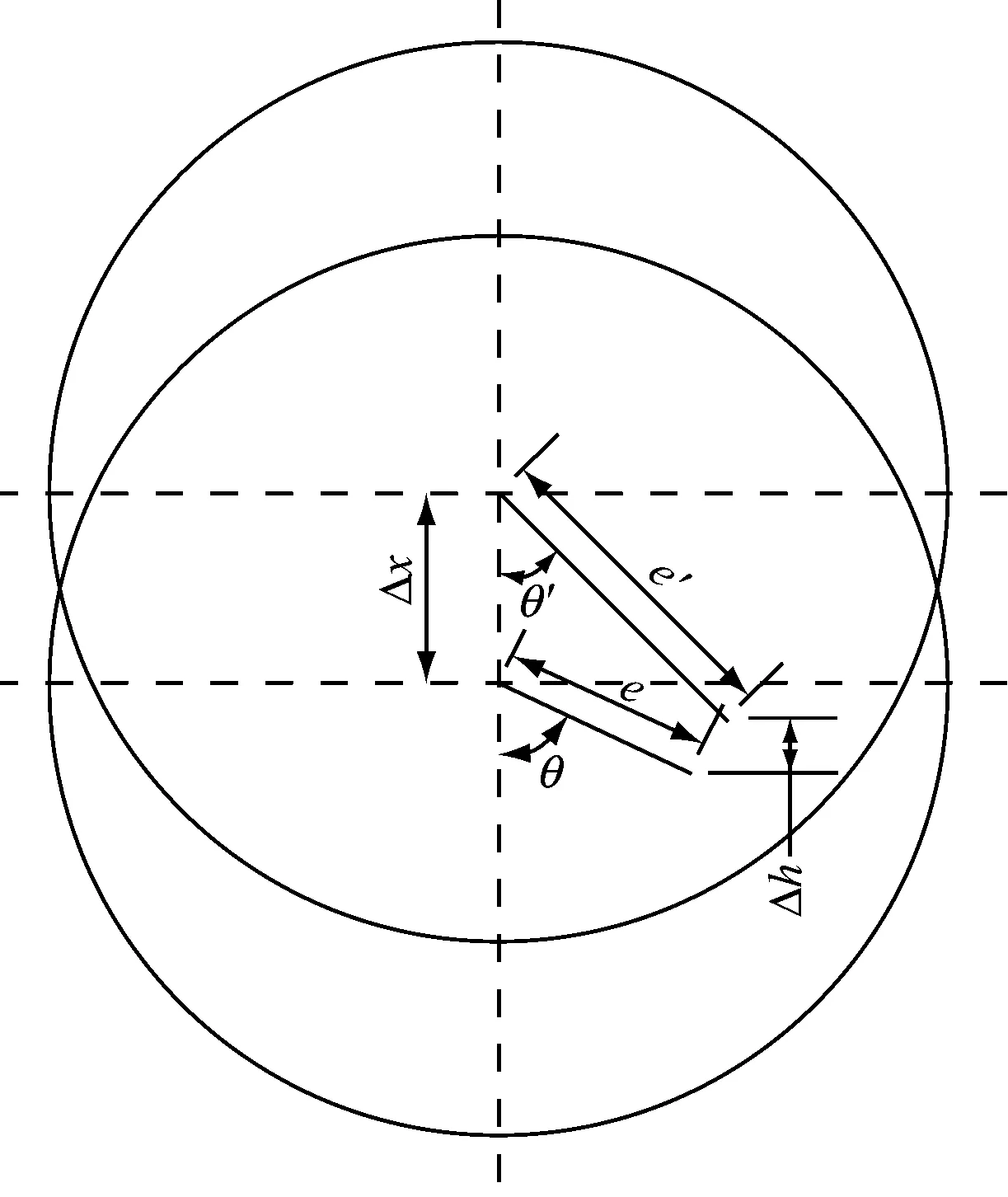
图1 轴承标高抬升时轴颈偏心距和偏位角变化
Fig.1 Changes of journal eccentricity and deflection angle in bearing elevation lifting
轴颈高度变化后,受转轴弹性变形影响,转子上其他截面高度也会相应改变。在弹性变形范围内,轴封间隙处轴高度变化量为:
Δs=k×Δh
(2)
式中:Δs为轴封间隙处轴高度变化量,即轴封间隙变化量;k为转轴弹性系数。
为了得到轴承标高调整量Δx所引起的轴封间隙处轴高度变化量Δs,需要分别计算轴承标高对载荷的影响、载荷对轴颈偏心距和偏位角的影响以及转轴弹性变形的影响系数。
1.1 轴承标高对载荷的影响
如图2所示,把轴系简化为集总质量模型,其中节点数为n,轴承数为m。
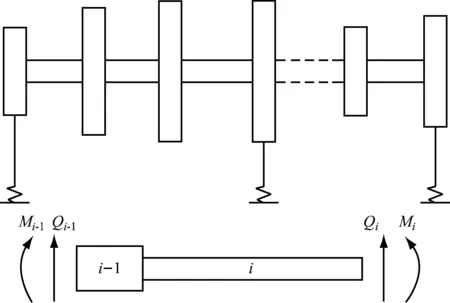
图2 多支撑转子系统模型
传递矩阵状态矢量为:
(3)
式中:y为节点位移;φ为节点转角;M为节点弯矩;Q为节点剪力;mg为节点重量;l为轴段长度;E为弹性模量;I为截面惯性矩;Fb,i为节点反作用力;i=2,3,…,n。
由节点传递关系有:
(4)
轴承节点状态矢量取位移项可展开得到m个方程。由于两自由端剪力和弯矩为0,分别列出2个方程。联立m+2个方程,求解得到m个轴承载荷和初始节点的挠度转角共m+2个未知量,并求出给定轴承标高下的轴系扬度曲线。
轴承标高抬升Δx后,通过上述传递矩阵法可计算出对应的轴承载荷变化。
1.2 载荷对轴颈偏心距和偏位角的影响
轴承载荷变化后,油膜厚度会发生相应变化,其影响可以通过求解雷诺方程得到:
(5)
式中:φ为圆周方向无量纲坐标;λ为轴向无量纲坐标;d为轴承内径;L为轴承宽度;H为无量纲油膜厚度;p为无量纲压力。
将求解区域离散化,采用差分法求解无量纲雷诺方程,逐点松弛迭代,引入雷诺边界条件,得到油膜压力分布。
无量纲油膜承载力W的表达式如下:
(6)
(7)
式中:Wx、Wy分别为W的水平和垂直分量。
根据轴承标高调整前后的轴承载荷,可以求得轴承标高调整前后的轴颈偏心距e、e′和偏位角θ、θ′,再根据式(1)可以得到轴承标高抬升Δx时轴颈高度的实际升高量Δh。
1.3 转轴弹性变形的影响
轴承刚支条件下,给定2组不同轴承标高,采用传递矩阵法计算出轴系扬度曲线。
转子在弹性变形范围内,各节点的高度变化满足线性关系。2组不同轴承标高下,轴系扬度曲线在轴封处和轴承处的高度变化量之比即为转轴弹性系数(见式(2))。
2 计算实例
某大型汽轮发电机组由高中压转子、低压转子和发电机转子组成,发电机转子外伸部分为励磁机转子。轴系共有6个轴承,总长约32.3 m,质量约164 875 kg。该机组轴系被模化为229个节点和228个轴段,机组模化简图如图3所示。各轴承参数见表1,理想安装扬度曲线下的轴承标高及载荷见表2。
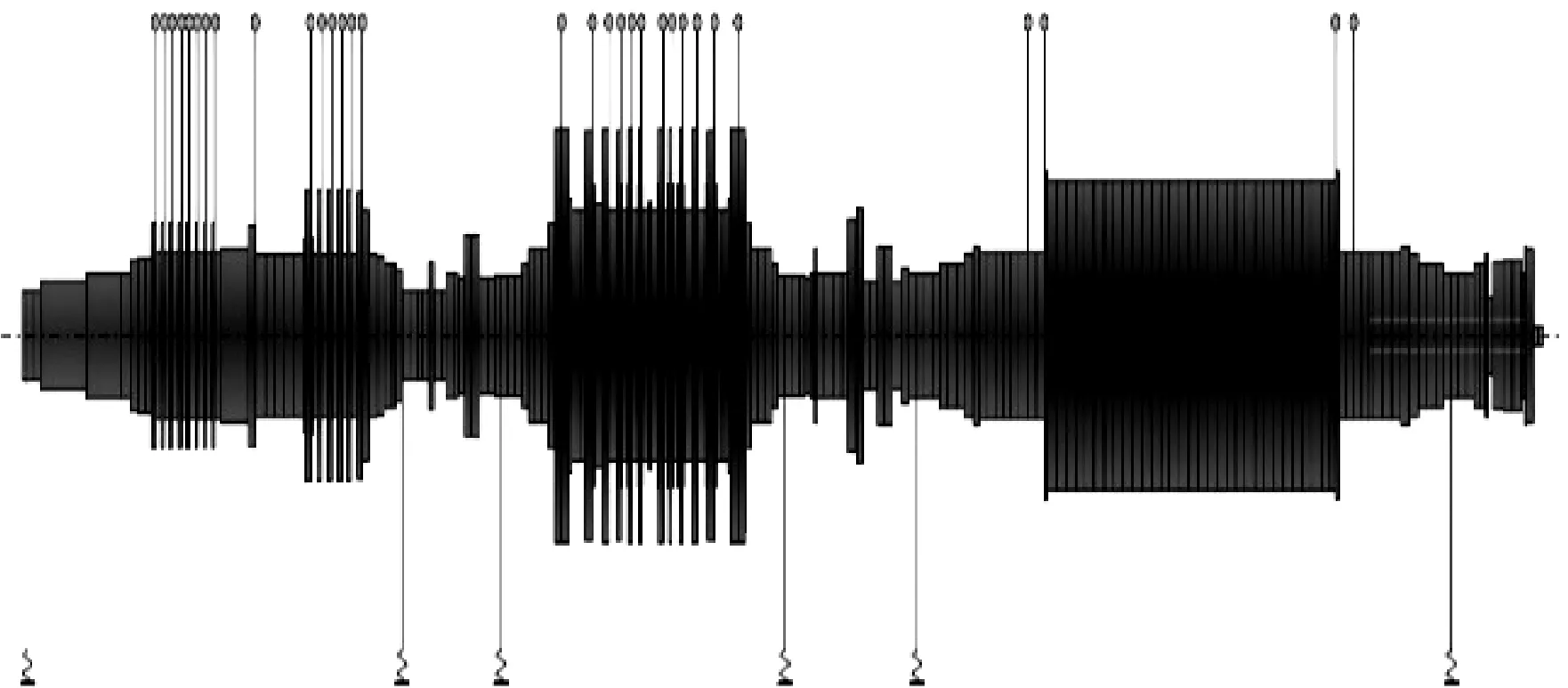
图3 轴系模型图
3 计算结果与分析
3.1 理想安装标高下
在理想安装标高下,轴系各转子连成一条光滑的曲线,联轴器不承受额外的剪力和弯矩。表3给出了1号~6号轴承在理想安装标高下的偏心距、偏位角和转轴弹性系数。

表1 轴承参数
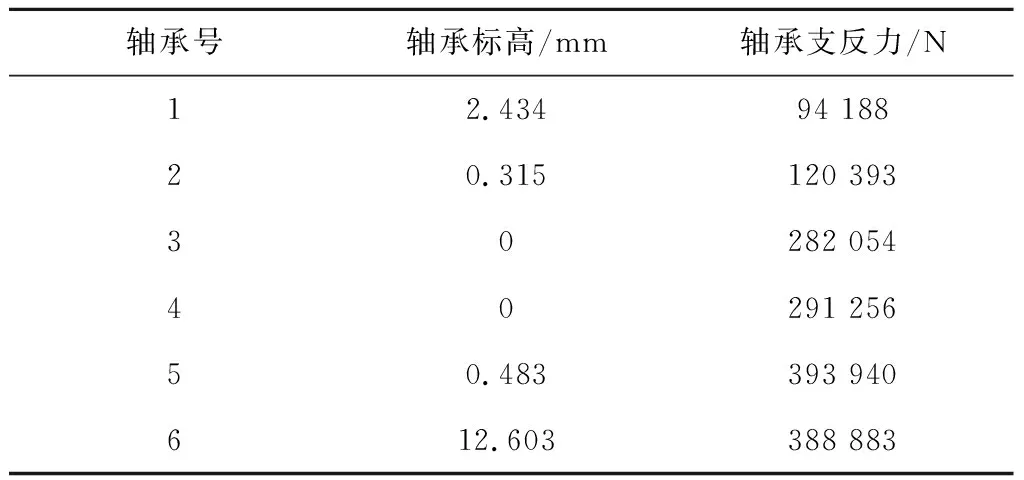
表2 理想安装扬度曲线下的轴承标高及载荷
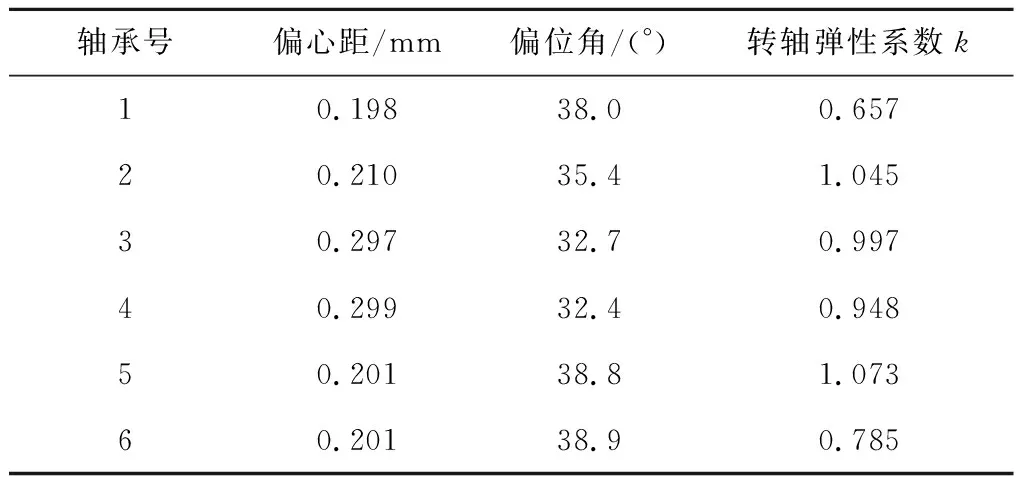
表3 初始参数计算结果
图4给出了1号~6号轴承标高抬升量从0增加到0.5 mm过程中,轴封间隙变化量与轴承标高抬升量比值Δs/Δx的变化曲线。从图4可以看出,中间轴承附近轴封间隙变化量与轴承标高变化量比值达到90%~105%,接近100%,说明中间轴承标高变化对相邻截面处轴封间隙影响较大;1号和6号轴承位于轴系两侧,属于自由端,Δs/Δx分别为66%和79%,说明自由端轴承标高变化对相邻截面处轴封间隙影响较小,轴封间隙变化对自由端轴承标高变化不敏感。为了解决机组振动故障,自由端轴承标高调整幅度可以大些。
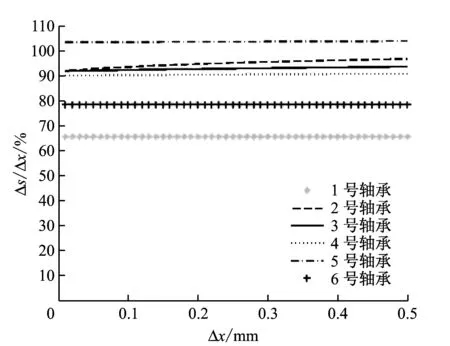
图4 1号~6号轴承轴封间隙变化量与轴承标高抬升量比值随轴承标高抬升量的变化
Fig.4 Ratio of seal clearance variation to elevation lift vs. elevation adjustment from bearing 1 to bearing 6
3.2 非理想安装标高下
受轴系安装偏差以及机组在冷态和热态下轴承标高变化等因素影响,实际轴承标高可能与理想安装标高之间有较大偏差,轴承可能会出现脱空或过载故障情况,进而引发振动故障。
图5给出了4号轴承在脱空、轻载、理想安装标高和过载4种情况下,轴封间隙变化量与轴承标高抬升量比值随轴承标高抬升量的变化情况。从图5可以看出,脱空或轻载状态下,油膜厚度较大,缓冲效果明显,轴封间隙变化量与轴承标高抬升量比值较小。轴承载荷较大时,油膜较薄,起不到缓冲效应,轴封间隙变化量与轴承标高抬升量相近。
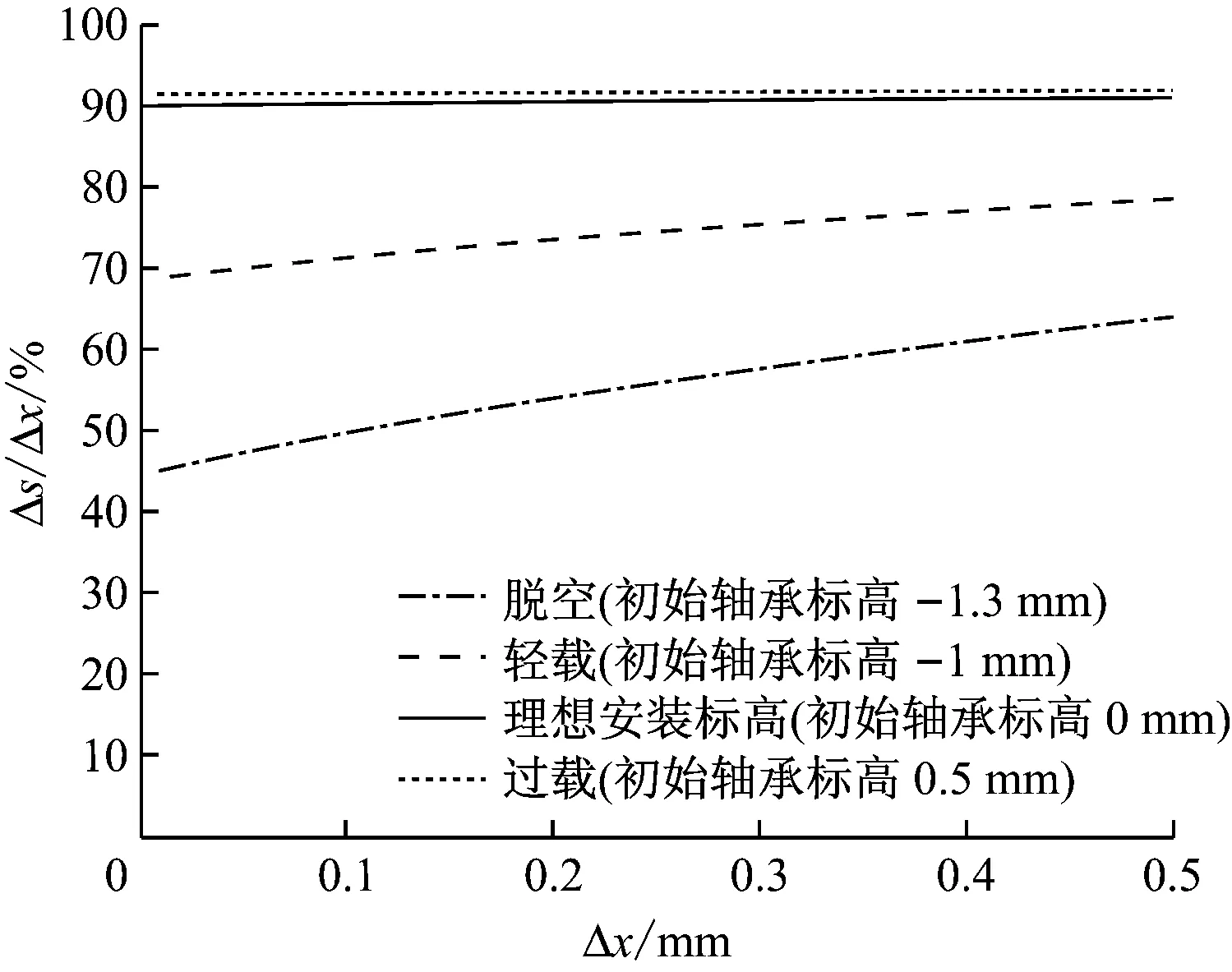
图5 故障状态下轴封间隙变化量与轴承标高抬升量比值随轴承标高调整量的变化
Fig.5 Ratio of seal clearance variation to elevation lift vs. elevation adjustment under fault conditions
3.3 转速影响分析
图6给出了轻载状态下4号轴承标高抬升0.5 mm后轴封间隙变化量与轴承标高抬升量比值Δs/Δx随转速的变化曲线。从图6可以看出,转速为0时,轴封间隙变化量仅受轴承标高变化和转轴弹性变形影响。随着转速的升高,油膜厚度增加,油膜缓冲效果逐渐增强,两者之间的比值逐渐减小。
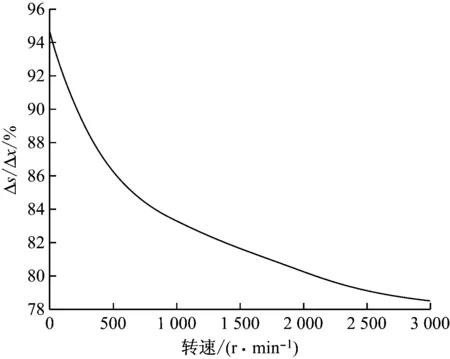
图6 轴封间隙变化量与轴承标高抬升量比值随转速的变化
Fig.6 Ratio of seal clearance variation to elevation lift at different rotating speeds
转速越低,轴封间隙变化对轴承标高变化越敏感。因此,在考虑轴承标高调整对轴封间隙影响时,还需考虑转速的影响。
4 结 论
(1) 受油膜、转轴弹性变形等因素的影响,轴封间隙变化量小于轴承标高调整量。
(2) 与中间轴承相比,自由端附近轴封间隙变化对轴承标高变化不敏感,故障治理时轴承标高调整幅度可以大些。
(3) 轴承载荷越小时,轴承标高调整对轴封间隙变化的影响越小。对于油膜振荡等失稳类故障,轴承本身就处于轻载或脱空状态,故障治理时轴承标高调整量可以大些。
(4) 转速较低时,油膜较薄,缓冲效果较弱,轴封间隙变化对轴承标高变化较敏感。轴承标高调整时还应考虑到启停机过程中低转速的情况。
参考文献:
[1] 于光辉, 杨灵, 陈利, 等. 轴承载荷不足引起的机组振动故障分析[J].润滑与密封, 2014, 39(11): 110-114.
YU Guanghui, YANG Ling, CHEN Li, et al.Analysis of abnormal vibration caused by insufficient load on bearing[J].LubricationEngineering, 2014, 39(11): 110-114.
[2] 张晓斌, 王永贞, 杨建刚. 某台汽轮发电机组轴承瓦温高原因分析[J].电站系统工程, 2014, 30(6): 48-49, 52.
ZHANG Xiaobin, WANG Yongzhen, YANG Jiangang. Research on reason of high bearing temperature occurred on turbine generator unit[J].PowerSystemEngineering, 2014, 30(6): 48-49, 52.
[3] 何文强, 杨建刚. 标高变化对轴系振动影响试验研究[J].电站系统工程, 2014, 30(6): 53-54, 58.
HE Wenqiang, YANG Jiangang. Experimental research on the influence of bearing elevation on shaft vibration[J].PowerSystemEngineering, 2014, 30(6): 53-54, 58.
[4] 杨建刚, 周世新, 黄葆华, 等. 多支撑汽轮发电机组轴承载荷灵敏度计算与分析[J].中国电机工程学报, 2000, 20(7): 79-82.
YANG Jiangang, ZHOU Shixin, HUANG Baohua, et al.Calculation and analysis of bearing load sensitivity for multi-support turbo-generator units[J].ProceedingsoftheCSEE, 2000, 20(7): 79-82.
[5] 田永伟, 杨建刚. 某1 000 MW汽轮发电机组轴承载荷灵敏度计算分析[J].热能动力工程, 2008, 23(5): 459-461.
TIAN Yongwei, YANG Jiangang. Calculation and analysis of the bearing load sensitivity of a 1 000 MW turbo-generator unit[J].JournalofEngineeringforThermalEnergyandPower, 2008, 23(5): 459-461.
[6] 夏志鹏. 多跨转子-轴承系统标高问题研究[D]. 上海: 复旦大学, 2008.
[7] 张世东, 杨建刚, 朱先宝, 等. 应变-传递矩阵法计算轴系载荷分布及实验研究[J].动力工程学报, 2012, 32(7): 513-516.
ZHANG Shidong, YANG Jiangang, ZHU Xianbao, et al.Experimental study of shafting load distribution based on strain and transfer matrix method[J].JournalofChineseSocietyofPowerEngineering, 2012, 32(7): 513-516.
[8] 李燕勇, 杨建刚, 董川, 等. 基于轴系对中数据的轴承载荷识别方法[J].动力工程学报, 2013, 33(12): 932-935.
LI Yanyong, YANG Jiangang, DONG Chuan, et al.Bearing load identification based on shaft alignment measurements[J].JournalofChineseSocietyofPowerEngineering, 2013, 33(12): 932-935.
[9] 杨涛. 汽轮发电机组动静碰摩故障分析及诊断方法研究[D]. 北京: 华北电力大学, 2011.
[10] 李军, 王春艳. 200 MW汽轮发电机组轴承振动异常原因分析及治理[J].吉林电力, 2014, 42(4): 49-51.
LI Jun, WANG Chunyan.Reason analysis and treatment for 200 MW turbo-generator unit bearing abnormal vibration[J].JilinElectricPower, 2014, 42(4): 49-51.
