基于神经网络的批量定制服装号型分类研究

袁惠芬，王 旭,2，齐雪良，刘新华,2

基于神经网络的批量定制服装号型分类研究

袁惠芬1，王 旭1,2，齐雪良1，刘新华1,2

（1. 安徽工程大学 纺织面料安徽省高校重点实验室，安徽 芜湖 241000；2. 安徽工程大学 纺织行业科技公共服务平台，安徽 芜湖 241000）

为提高批量定制服装号型的分类效率，运用神经网络方法，以男衬衫为研究对象，用6个测量项目（身高、胸围、腰围、颈围、肩宽和全臂长）为分类变量，对686名男性人体号型进行K-means聚类分析，并将聚类结果作为样本，对神经网络进行训练和测试。以混淆矩阵为指标研究了不同网络结构、训练算法及传递函数的分类效果。研究表明，分类效果随训练算法、网络结构不同存在明显差异，其中标准BP算法分类效果最差，弹性BP算法分类效果最好，且分类效果随隐层神经元数量的增加而提高，隐层和输出层传递函数均为logsig时，分类效果最好。

批量定制；号型分类；聚类分析；人工神经网络；混淆矩阵

批量定制是职业服装常见的加工方式，具有低成本、高效率的优点。号型分类是批量定制生产的重要环节。传统的号型分类主要依赖人工进行，分类效率低且易造成分类错误。如何提高分类准确性及分类效率成为定制服装企业和科研人员关注的焦点。目前针对服装号型分类的研究包括K-means聚类、择近分类、最小距离分类等。文献[1]以国标号型为基准，采用K-means算法对219名女性体型进行了聚类分析，并讨论了如何确定最佳聚类数及迭代次数。文献[2]选择了64个国标号型为参考点，以择近方式对男西服进行了号型分类。文献[3]提出以量体尺寸和成品规格尺寸的误差平方和为合体性指标，并将个体归入误差平方和最小的类别，以此作为批量定制号型分类的依据。文献[4]考虑到不同年龄段女性体型差异，运用有序样本最优分割法，得出了青年、成熟和中老年女性体型分类的特征变量。文献[5]以国标男子服装号型5.4系列和5.2系列分档规定为参考，提出基于最小距离法的男子上衣号型智能推荐算法，并通过计算机实现纸样的快速生成。文献[6-8]采用统计分析的方法，分别研究了东北、福建及江浙地区女性体型特点，并提出Y、A、B等不同体型控制部位的推荐档差。上述关于号型分类的研究大多采用聚类分析方法，其分类结果易受初始聚心及分类数的影响而不稳定，且需要人为干预而影响分类效率。近年来，随着人工智能的发展，经过训练的神经网络在号型分类、规格尺寸自动生成等方面体现出准确性好、效率高的优点[9-11]。

为提高号型分类效率，本文以男衬衫号型分类为研究对象，以身高、胸围、腰围、颈围、肩宽和全臂长为分类变量进行聚类分析，并将聚类结果作为训练样本，对建立的神经网络进行训练和测试。以分类正确率为指标研究了不同网络结构、训练算法及传递函数的分类效果。研究结果为提高批量定制服装号型分类效率提供了参考。

1 试验部分

1.1 数据分析流程

号型数据分析流程如图1所示，包括网络训练样本数据的准备、网络建立、网络训练、网络输出和分类效果评价等过程。

训练样本数据由量体数据经改进的K-means聚类分析后产生。BP网络的建立包括网络层次结构、各层神经元数量和传递函数的选择。BP网络的训练，即通过训练样本不断调整网络权值和偏置值，使网络性能指数不断优化。最后通过混淆矩阵表示的网络输出和目标向量的差异，对网络的分类效果进行评价。

图1 数据分析流程图

图2 人体测量项目示意图

1.2 训练样本数据准备

训练样本是已具有分类标记的数据，其作用是通过多次训练并不断调整神经网络的权值和偏置值，以提高号型分类的正确率。本次试验训练样本数据来源为686名成年男性定制衬衫，6个测量项目包括：身高、胸围、腰围、颈围、肩宽和全臂长（见图2）。参考文献[12]采用的改进K-means聚类算法对数据进行聚类，并将结果作为神经网络的训练样本。 686个量体数据，最终被聚为12个类别，即网络输入向量为686个列向量，每个列向量为6行1列，分别表示6个量体数据，其对应的目标向量为686个列向量，每个列向量为12行1列，元素1所在的行表示其归属的号型类别，其他行元素均为0。

1.3 神经网络的建立

多层前向BP网络由多个神经元层构成，每层有多个神经元，神经元是一个多输入单输出的信息处理单元。理论上已证明，两层(一个隐层和一个输出层)BP网络可实现任意非线性映射，故本次试验选择两层BP网络，其结构如图3所示。

图3中，表示输入向量，表示输入节点数，、和a分别表示神经元数量、传递函数和输出，和分别表示网络权值矩阵和偏置值向量，其中上标1、2分别表示隐层和输出层。图2的网络结构可简记为-1-2，其中由的维数决定，本次试验输入向量为6维，故=6。输出层的神经元数2由目标向量的维数决定，本次试验目标向量为12维，故输出层神经元数为2=12。隐层神经元数1一般采用试探的方式进行，为减少计算和存储，在满足预定精度的条件下，隐层神经元的数目以少为宜。传递函数，包括非线性函数logsig、tansig和线性函数purelin等，不同的传递函数会引起网络输出的变化，通常可根据对比试验，选择分类正确率高的传递函数。

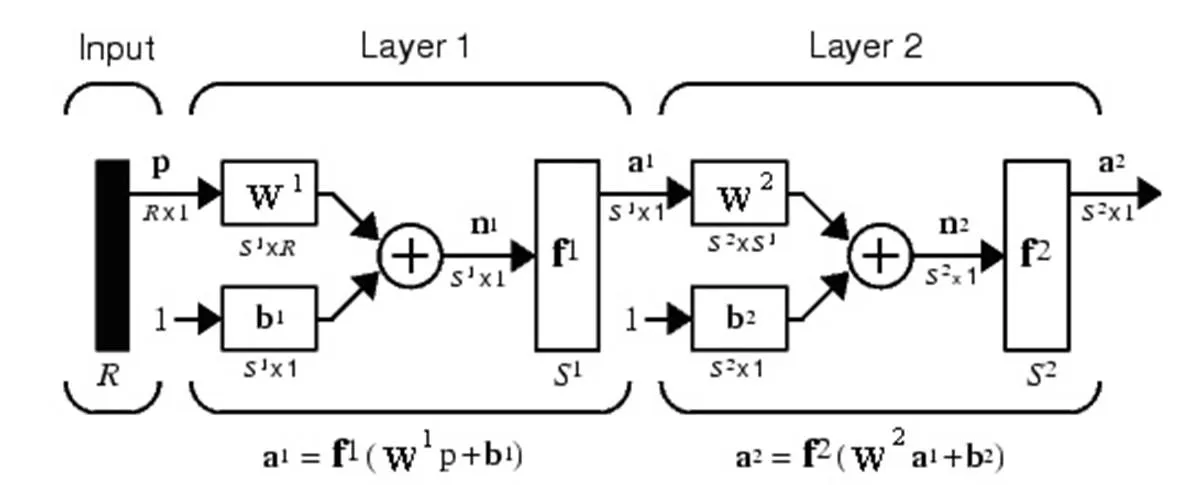
图3 两层BP网络结构示意图

1.4 网络训练算法

网络训练的目的是通过调整网络参数来优化网络性能，使网络输出和目标更加接近。通常定义网络输出和目标间的均方误差()，作为反映网络性能指数的定量标准，网络训练算法就是搜索能不断减小()的参数空间的算法，如最速下降法、牛顿法、共轭梯度法，以及上述算法的改进。

1.4.1 最速下降法

最速下降法是对()按式（1）进行一阶Taylor级数近似展开的迭代算法。利用迭代点处的一阶导数(梯度)对()近似，沿()负梯度方向不断形成新迭代点，直至满足精度要求。

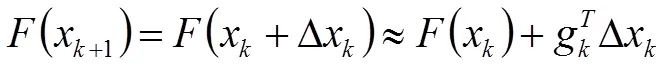
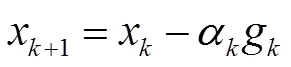
1.4.2 牛顿法

牛顿法是对()按式（3）进行二阶Taylor级数近似展开的迭代算法.利用迭代点处的一阶导数(梯度)和二阶导数(Hessian矩阵)对()近似，并取使()达极小点的迭代点作为新的迭代点，并不断重复，直至满足精度要求。

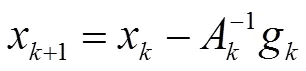
1.4.3 共轭梯度法

当向量集合{}对正定Hessian矩阵两两共轭，即满足式（6）.

那么，共轭梯度法满足迭代式（7）。

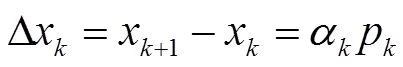
最速下降法仅以当前迭代时F(x)的负梯度方向对网络参数进行修正，没有考虑到梯度变化的趋势，实际应用时，易出现振荡、收敛缓慢及陷入局部极小等缺点，可通过启发式改进或数值优化处理，前者包括附加动量、可变学习率、有动量可变学习率、弹性梯度下降法等，后者包括拟牛顿法、Levenberg-Marquardt等方法。Matlab神经网络工具箱中均提供上述算法的训练函数。

1.5 分类效果评价

混淆矩阵（Confusion Matrix）是评价神经网络分类效果的常用指标之一，其表达式见式（8）。混淆矩阵的每一列代表网络输出类别，每一列元素的总和表示网络输出为该类别的数量。每一行代表了数据的实际类别，即目标向量反映的类别，每一行元素的总和表示该类别数据的实际数量。其中主对角线元素c表示网络输出为第类，实际也为第类。非对角线元素c则表示实际为第类，而网络输出却为第类.如果主对角线上元素数值大，则表明网络的输出和实际类别一致，说明网络分类效果好，反之则说明网络分类效果不好。

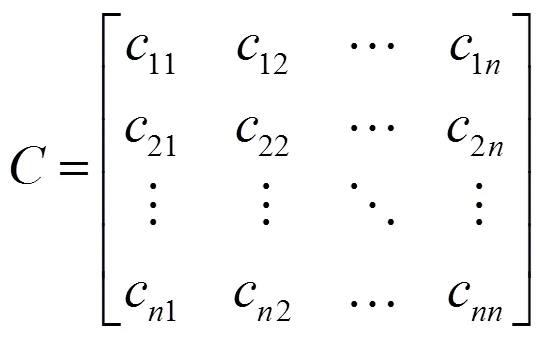
由于目标列向量，用元素1所在的行表示类别，其余行元素均为0，而网络输出结果则可能出现各行均为非0元素的情况，此时可通过对网络输出神经元进行竞争处理，即网络输出层神经元最大值竞争获胜，元素为1，而其他神经元则均竞争失败，元素均为0。

2 结果与讨论

2.1 影响网络分类效果的因素

训练算法、网络结构参数及传递函数的不同均对网络分类效果产生影响，其中训练算法的影响最为明显。有监督网络训练目的是调整网络参数，使网络输出和目标更加接近。通常定义网络输出和目标间的均方误差为衡量网络性能的定量指标，并逐步搜索减小该指标的参数空间，以优化网络性能。网络层数、各层神经元数量和传递函数等网络结构的变化，对网络分类效果也产生一定的影响。

通常网络建立后会随机赋予网络权值矩阵和偏置值向量一个初值，初值不同会对网络训练产生影响。为避免网络因过度拟合而导致泛化能力差，可通过及时停止训练来解决，即先将输入向量随机分成训练、验证和测试集。训练集负责训练并调整和.验证集参与训练并监控误差，随和的调整，开始阶段验证集误差逐渐下降，如果出现过度拟合则验证集误差会提高并计验证错误次数1次，当验证错误次数超过预定次数时，即停止训练，以此时的和作为训练后的网络参数。测试集是未经训练的数据，用于考察网络对未知数据的分类效果。本次试验和的调整采用批处理方式，即完成所有输入向量的训练后，再修改和。

2.2 不同训练算法的分类效果

所有试验数据处理在CPU频率3.0GHz，内存4GB的计算机上进行，其中神经网络的建立和训练软件为Matlab 7.6自带神经网络工具箱。图4为采用标准BP算法的训练过程示意图，其中网络输入节点6，隐层、输出层的神经元数量分别为40和12，隐层和输出层传递函数均为logsig，终止训练条件为迭代1000次或性能指数小于等于10-3。

图4 标准BP算法训练过程示意图

分别用相同的网络结构和传递函数比较了标准BP算法（最速下降法）、可变学习率BP算法、弹性梯度下降法、拟牛顿法、Levenberg-Marquardt法、共轭梯度法等6种不同训练算法的分类效果.每种训练算法共执行10次，取分类正确率最高的进行比较，其结果如表1所示。

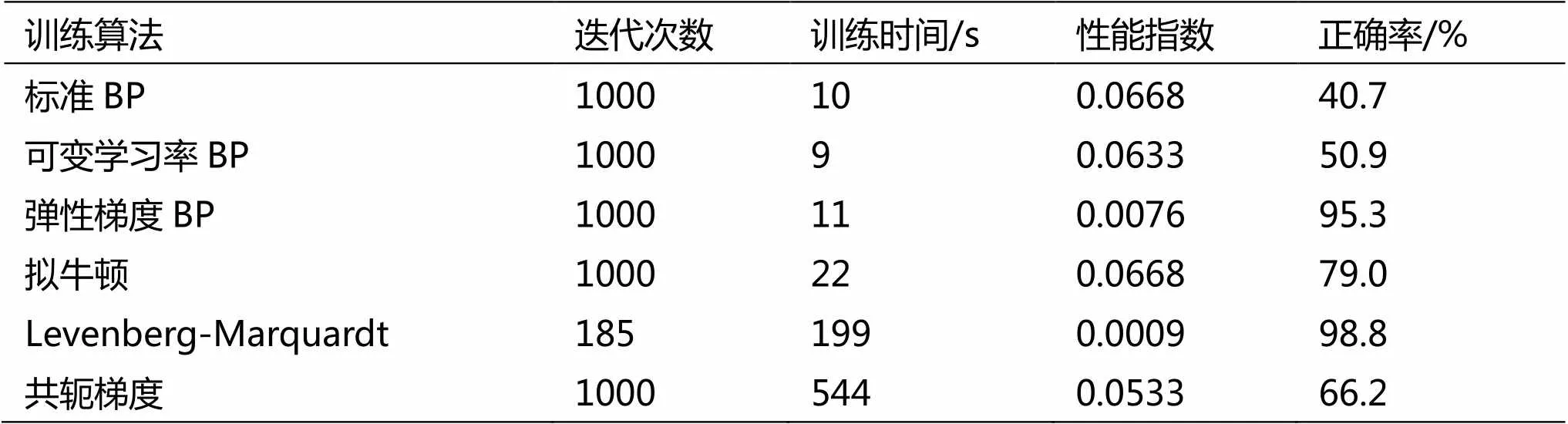
表1 不同训练算法的分类结果

通常性能指数越低，说明网络输出和目标越接近，分类效果越好，即分类正确率越高。由表1可看出，除了Levenberg-Marquardt法是达到性能指数网络训练终止外，其他算法均达到最大迭代次数而网络训练终止.从正确率来看，标准BP算法分类正确率仅40.7%，可变学习率BP算法、共轭梯度法和拟牛顿法分类正确率有所提高，分别达到50.9%，66.2%和79.0%，上述4种算法训练的网络对于号型分类，几乎没有实际运用价值。弹性梯度法和Levenberg-Marquardt法，分类正确率是最好的两类，分别为95.3%和98.8%，虽然弹性梯度法在分类正确率上略低于Levenberg-Marquardt法，但训练时间上明显优于Levenberg-Marquardt法。

综上分析，6种算法中，弹性梯度法具有分类正确率高且训练时间短的优点，适合作为号型分类神经网络的训练算法。

2.3 不同网络结构的分类效果

根据2.2小节，选择弹性梯度算法考察了不同的隐层神经元数量和传递函数时的分类效果。其中隐层和输出层传递函数，分别采用logsig-logsig、logsig-purelin、logsig-tansig、purelin-purelin等4种搭配形式。隐层神经元数量从20个，每次递增20个至80个为止。终止训练条件为迭代5000次或性能指数小于等于10-3。每种网络结构共执行10次，取分类效果最好的结果进行比较。表2为不同网络结构下的分类正确率。

表2 不同网络结构的网络输出

由表2看出，当隐层和输出层传递函数均为logsig时，随隐层神经元数量从20个增加到80个，分类正确率从91.5%逐渐提高到98.2%。这说明隐层神经元个数的提高，有利于提高网络的分类正确率。当隐层和输出层传递函数分别为logsig、purelin时，随隐层神经元数量从20到80的增加，分类正确率从69.2%逐渐提高到87.9%。当隐层和输出层传递函数分别为logsig、tansig时，随隐层神经元数量从20到80的增加，分类正确率从71.4%逐渐提高到81.1%。当隐层和输出层传递函数分别为purelin、purelin时，随隐层神经元数量从20到80的增加，分类正确率从32.1%逐渐提高到47.2%。

表2的结果说明，隐层和输出层两种不同传递函数的搭配方式，均随着隐层神经元数量的递增，分类效果逐渐提高，且隐层神经元数量相同时，隐层、输出层传递函数均为logsig时，分类效果明显优于其他网络结构。

3 结论

以混淆矩阵为指标，采用BP神经网络考察了批量定制男衬衫的号型分类效果，结论如下：

（1）分类效果随训练算法不同存在明显差异，其中标准BP算法分类效果最差，弹性梯度法和Levenberg-Marquardt分类效果好，正确率分别达95.3%，98.8%，且弹性梯度算法训练时间短，更适合作为号型分类神经网络训练算法。

（2）弹性BP算法分类效果随网络结构不同存在明显差异，当隐层和输出层传递函数均为logsig时，分类效果优于其他情况，且随隐层神经元数量从20增加到80，分类正确率从91.5%提高到98.2%。

[1] 方方，王子英．K-means聚类分析在人体体型分类中的应用[J]．东华大学学报（自然科学版），2014，40(5)：593-598．

[2] 王建萍，李月丽，喻芳．基于择近原则的服装号型数字化归档方法[J]．纺织学报，2007，28(11)：106-110．

[3] 张恒，张欣．基于批量定制的服装号型归档方法[J]．东华大学学报(自然科学版)，2009，35(4)：436-440．

[4] 尹玲，张文斌，许才国．基于有序样本最优分割法的女性体型分类[J]．纺织学报，2014，(09)：114-119．

[5] 卢丹，郝矿荣，丁永生．男上装个性化纸样的快速生成方法[J]．东华大学学报(自然科学版)，2014，(03)：311-317．

[6] 潘力，王军，沙莎，等．东北地区青年女子体型分类与服装档差研究[J]．纺织学报，2013，(11)：131-135．

[7] 黄灿艺．福建地区青年女性体型划分与尺寸分档[J]．纺织学报，2012，(05)：111-115．

[8] 张金花，王宏付．江浙女青年中心号型及各围度部位档差分析[J]．纺织学报，2011，(09)：100-103．

[9] 孙洁，金娟凤，倪世明，等．基于神经网络集成的女下装号型归档模型构建[J]．纺织学报，2013，(08)：110-114．

[10]王竹君，李婷玉，邢英梅，等．改进型BP网络在男西服规格尺寸自动生成上的应用[J]．武汉纺织大学学报，2014，(06)：36-39．

[11]于辉，郑瑞平．基于BP神经网络的MTM中合体服装样板生成研究[J]．北京服装学院学报(自然科学版)，2013，(01)：35-41．

[12]齐雪良，袁惠芬，王旭．上海地区成年女性批量定制服装号型分类研究[J]．武汉纺织大学学报，2016，(04)：8-12．

Investigation on Mass Customization Clothing Shape Classification by Artificial Neural Network

YUAN Hui-fen1, WANG Xu1,2, QI Xue-liang1, LIU Xin-hua1,2

(1. Anhui Provincial Key Laboratory of Textile Fabric, Anhui Polytechnic University, Wuhu Anhui 241000, China；2. The Science and Technology Public Service Platform for Textile industry, Anhui Polytechnic University, Wuhu Anhui 241000, China)

In order to accelerate shape classification efficiency of mass customization clothing, artificial neural network method was applied. Take man shirt for example, 686 male body data was classified by K-means algorithms with 6 variables (height, bust circumference, waist circumference, neck circumference, shoulder width and arm length) to generate sample for training and testing neural network. Then, classification accuracy rate of network was studied by confusion matrix with different structures, training algorithms and transfer function. The results revealed obvious difference of classification accuracy rate existed in network with different training algorithms and structure. The lowest classification accuracy rate came from standard BP algorithms, while the highest one came from resilient BP algorithms. The classification accuracy rate increased with the increase of the neuron number of hide-layer. The best classification came from logsig transfer function both used in hide-layer and output-layer.

mass customization; shape classification; clustering analysis; artificial neural network; confusion matrix

袁惠芬（1972-），女，教授，研究方向：服装数字化.

安徽省教育厅质量工程项目（2015sjjd012）；安徽省高等教育振兴计划项目（2015zdjy087）；安徽工程大学服装工程特色专业（2016tszy009）.

TS 941.7

A

2095－414X(2018)03－0041－05