分形理论在服饰印花图案设计中的优势与应用

窦林贤



分形理论在服饰印花图案设计中的优势与应用

窦林贤

（安徽农业大学 经济技术学院，安徽 合肥 230041）

基于分形理论的分形图形可以为服饰印花图案设计提供新的手段和思路，具有重要的理论意义和实践价值。文章基于分形理论的基本内涵分析其在服饰印花图案设计中的可行性，详细探讨基于分形理论的服饰印花图案构成形式以及在服饰印花图案设计中的实践应用。

分形理论；分形图形；服饰印花图案

1 分形理论

分形理论产生于上世纪七十年代，其创始人为著名数学家曼德勃罗。他在1975年出版的关于分形的著作《分形：形状、机遇和维数》一书中认为分形的意思是分数的、不规则的和破碎的，并以此描述那些自然界中不能利用简单的几何图形、几何关系描述的复杂对象，例如弯曲的河岸、变化的云朵、纵横交错的枝条等。上述事物的共同特征是不规则性和不光滑性，或者说都是分形。分形理论与我国某些传统哲学理念不谋而合，例如老子的《道德经》中就有“道生一、一生二、二生三、三生万物”的论断，可谓与分形理论不谋而合。

不仅自然界存在诸多揭示上述理论的自然作品，人们也可以基于分形理论创造出诸多美轮美奂的图案。虽然分形理论属于数学领域的新生概念，其理论仍处于形成和发展时期，但是基于分形理论的分形几何图案仍具有以下两大显著的特点：一是分形几何图案具有十分精细的结构，即使进行无限小尺度的细分，也能呈现出复杂的细节[1]。这不仅与无限可分的哲学观相吻合，也可以彰显图案本身的丰富性；二是分形图形往往具有高度的自相似性，其组成部分与整体以某种形式相似，呈现出奇妙的图形特征。总之，分形图形属于一种微型化的奇迹，其中的每一个图形都可以看做微型化的整体，既分散又完整，从而打破了传统图形的整体与部分的隔膜，从而可以利用简单的数学公式复制极为复杂的自然特征。

分形理论于上世纪八十年代影响到我国，在随后的时段内获得了巨大的发展，广泛应用于生物医学、气象地理、经济、艺术合集以及自然科学领域。大部分的文献研究是基于数学以及计算机图形学基础的分形图形形成和表达，包括L系统、IFS迭代函数系统以及复动力系统的分形集。在纺织服装行业，王小铭于2001年基于分形的自相似性创造出新奇美丽的纺织品分形图案设计作品若干；2003年陈有卿服装面料图案和分形艺术之间的关系以及L系统自动生成纺织品图案。2007年郑天勇出版了《纺织品CAD/CAM》一书，详细阐述了分形图形在纺织品中的应用。2015年代沛涵对分形图形进行分类并运用到纺织品设计中。分形在纺织服装领域的运用多是利用分形理论生成绚丽的图案，但是针对特定风格的图形研究较少。

2 分形理论在服饰印花图案设计中的优势

分形理论属于一个新型概念，虽然尚未形成一个完整的逻辑体系，却并未影响其在各个学科领域得到迅速而广泛的应用。随着新世纪以来计算机和数字技术的迅速发展，基于分形理论的分形图形设计具有了生成便捷、种类繁多、结构复杂的特性，促进了其在服饰印花图案设计中的应用，已经成为服饰印花图案设计设计研究的重要课题。

分形几何图案为服饰印花图案设计提供了丰富的素材[2]。分形点、分形线、分形面以及分形色彩的组合、安排和运用，均可以塑造出不同的图像设计效果。以三分康托集为例，其主要特征是不断去掉中间的三分之一部分，并使图形按照一种独特的规则从大到小排列。将其以用于服饰印花图案设计，可以产生良好的视觉效果。总之，分形图形中蕴含有无限的嵌套结构，利用分形理论可以对服饰印花图案设计具有一定的指导作用。

与传统的图案设计相比，分形图案无论在生成方式还是图案的美感呈现方面都具有巨大优势[3]。在图案的对称结构设计上，传统图案设计只有简单的轴对称和中心对称，而分形图案则是局部与整体之间的更为复杂的对称，使整个图案在结构方面显得更为精致和细腻。在图案的色彩层次上，分形图案基于其特殊的生成方式可以有效突破传统图案设计的套色限制，凭借更为丰富的色彩层次感塑造强大的视觉冲击。因此，分形图案的出现，为服饰印花图案设计的另辟蹊径提供了可能，必将得到更为广泛的应用。

服饰图案设计的主要目的是通过图案的运用，使服装整体看上去更加美观得体，而分形理论恰巧是一种能够创造出许多美丽图形的基本理论。因此，将分形理论用于服饰图案设计，可以为设计师提供一种全新的思路和设计理念，也可以促发和放飞设计师的创作灵感，创造出更多的服装图案，提升服饰设计水平。

3 基于分形理论的服饰印花图案设计与应用方法

在分形图形出现以来，研究者基于分形理论和计算机技术在分形几何图案生成研究方面取得了一系列成果[4]。我们可以利用上述研究成果，对基本的分形图形进行变形、旋转、复制等进一步构成设计，将其用于服饰印花图案设计，下面就具体的设计思路和应用方法进行进一步探讨。

3.1 单独纹样设计与应用

在服饰印花图案设计中最基本的组织形式就是单独纹样，也就是在图案本身是独立存在的，在其周围并不存在与其他形态的连接和连续关系。由于单独纹样没有外观方面的限制，因此可以单独作为装饰纹样使用，也可以与其他纹样相互组合构成更为复杂的图案。由于单独纹样经常独立使用，因此在设计上讲究结构清晰、主次分明，能够直接反映图案形态和精神。

从形态布局来看，单独纹样可以分为对称式和平衡式两种基本的布局方式。其中，对称式的特点是图案的结构具有整齐性的突出特征，也就是以对称轴或中心点形成上下、左右或多面对称，如图1中的图案是对称式分形图案，以圆为中心，使上下、左右对称，不管是小的元素还是大的元素都彼此制约相互抗衡形成一个整体；平衡式单独纹样的特征是结构比较灵活，无论是造型还是空间形式均不受对称中心和对称轴的限制，使图案的主体更为突出，形象更为舒展和飘逸，如图2中的图案是单独纹样中的平衡式图案，主要是以一个基本形为元素，截取其中的某一部分，进行不断的迭代与重复，形成新的图形。在视觉上给人无限延伸的视觉效果。

图1 对称式单独纹样

图2 平衡式单独纹样

3.2 适合纹样设计与应用

适合纹样指的是外形中适合三角形、方形、圆形、梅花型等多种常见外形的图案构成，这种纹样构成具有美观、形象、生动、以及结构严谨和色彩丰富的特征，不仅可以单独使用，亦可以作为基本纹样进行组合构成设计。适合纹样与单独纹样类似，也可以分为平衡式和对称式两种构成形态。其中，对称式主要有向心、离心、直立、旋转等多种形式，见图3，平衡式的构成的主要特征是比较自由，但是在构成设计时需要注意疏密、虚实和方向等空间布局。

图3 适合纹样的几种形式

3.3 连续纹样设计与应用

顾名思义，连续纹样是以单独纹样或适合纹样为单元，向两个或四个方面连续发展，从而形成条状或一定篇幅的图案。连续纹样是分形图案构成设计中最为复杂的形态，具有连续性、结构性和韵律美。根据发展方向的不同，连续纹样可以分为二方连续纹样和四方连续纹样。

二方纹样是由一个图案基本单元向左右或上下两个方向进行连续排列发展，形成反复排列的条带状图案，因此又叫做带状纹样或花边，见图4。由于这种纹样是依据重复连接的方式生成的，因此可以体现出鲜明的节奏感、韵律感和规则感。根据具体的设计和表现形态，二方连续纹样又可以分为散点式、直立式、波纹式、斜线式和综合式等五种基本的构成形式。结合二方连续纹样的生成形态，在设计时需要注重不同单元之间的连接关系处理，实现在主宾、疏密、动静上的适合和得当，尽力避免生硬连接或缺乏连贯性与整体性。以散点式为例，由于其基本纹样为点元素，在设计时需要处理好点与点之间的关系，对于点来说这种关系主要表现在距离上，如果太远就缺乏呼应感，也不能太近，否则就会产生生硬和拘束的视觉感受，都不利于审美效果的彰显和发挥。

图4 二方连续纹样

图5 四方连续纹样

图6 边缘纹样

四方连续纹样是服饰印花图案设计中使用最广泛和最重要的一种，同时也是二方连续纹样的发展趋势。由于是一个元素通过向四方连续发展形成的，因此具有显著的网状结构，主要用于大面积的装饰设计，如地毯纹样、花布纹样、墙纸纹样等，见图5。从单元的组织和使用的骨架方面分析，四方连续纹样主要包括散点是、连缀式和重叠式等主要形式。基于这种构成方式的特征，在设计时主要应该考虑单位形象的凸显，同时又要注意图案在整体上的匀称和协调，防止出现空白和凌乱的关系。以重叠式纹样设计为例，其中的底纹主要是衬托上层浮纹的作用，因此在设计时底纹和浮纹要采用不同的形状、色彩和大小，以凸显图案的层次性和空间感。

3.4 边缘纹样设计与应用

边缘纹样是一种适合于外形周边的装饰纹样，其主要功能对主体花纹进行衬托，增强图案整体上的丰富性和层次性，见图6。因此，好的边缘纹样往往能够起到画龙点睛的作用，使中心花纹更加精美。当然，有些精致的边缘花纹设计也可以单独装饰。在纺织品印花设计中，可将边缘纹样用于服装、地毯以及窗帘的周边装饰。从构成来看，边缘纹样主要有平衡、对称和连续三种主要形式，可以依靠一个或多个基本单位，向左右两个方向连续。

4 分形理论在服饰印花图案设计中的应用

基于分形理论的服饰印花图案设计实践主要是依据分形图案的视觉艺术特点，从自然界以及现有的各种设计艺术风格中寻求设计灵感，从而构建起一种新的艺术表达途径。其总体实现思路为寻求设计灵感—选择分形图形素材—对照设计灵感—整体设计构思—利用计算机软件进行二次构思—模拟设计效果。下面以丝巾和服装面料为例阐述分形理论在印花图案设计中的实践应用。

4.1 在丝巾印花纹样中的应用

丝巾是女士在日常生活使用最为广泛的服装配饰，是彰显佩戴者文化特征、审美情趣和生活习惯的重要载体。从丝巾设计角度来看，图案是丝巾的灵魂，同时也是吸引消费者的重要因素。因此，将具有时代感的分形图案用于丝巾设计，不仅可以带来新的元素，也可以在相当程度提高丝巾的审美属性。结合丝巾设计的具体需求和上文提到的分形图案设计方式，可以设计出具有独特艺术魅力的丝巾印花纹样。例如，对称是一种最为常见的图案形式，与丝巾设计具有天然的契合性。当然，在具体的设计过程中可以不追求绝对性的对称，只要保持两侧的结构在视觉上基本一致即可，这样不仅可以展现韵律性美感，同时也可以体现出生动活泼、富于变化的艺术美感。基于上述设计思路，以三个单独纹样为主，见图7，结合其他纹样进行旋转、组合设计，可以获得如图8所示的丝巾纹样。

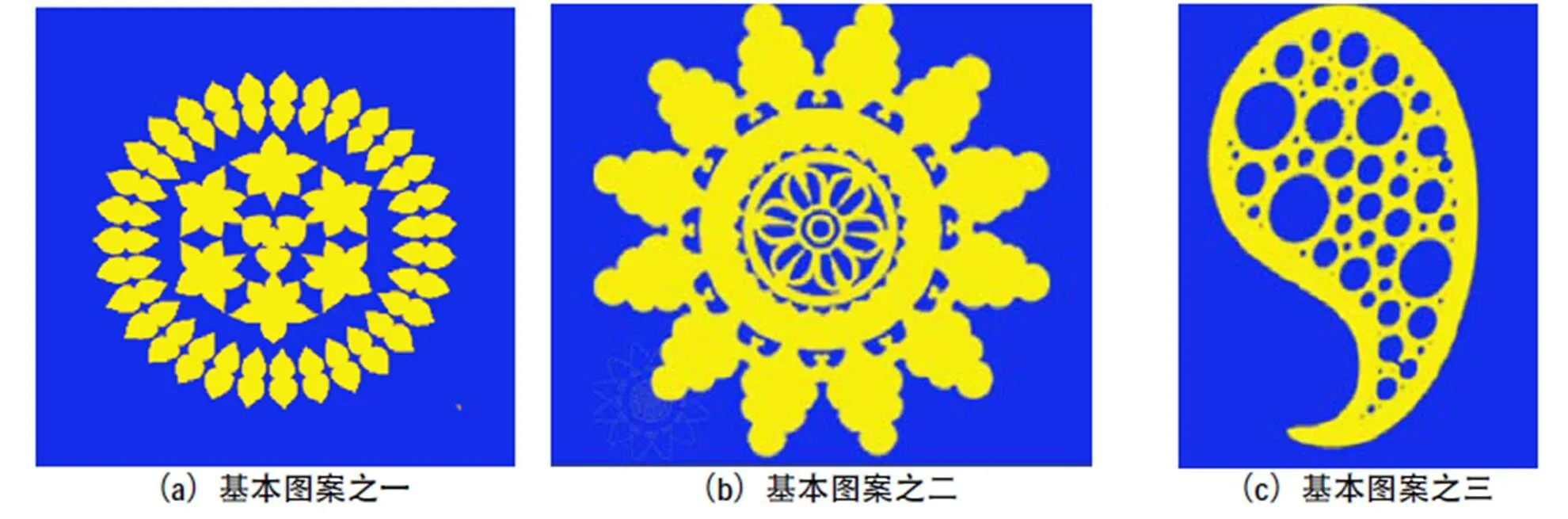
图7 三个单独纹样

4.2 在服装面料印花纹样设计中的应用

作为重要的审美元素，图案被广泛应用于服装设计领域，可以大幅提升服装面料的美学效果。因此，图案和材料、色彩和款式共同构成了现代服装面料设计的四大要素。基于分形理论的分形图案用于服装面料图案设计，不仅可以强化服装本身的时尚感和艺术感，同时也可以满足人们对服装设计完美化的时代追求，具有广阔的应用前景。由于面料的大面积和平面化特点，使用最多的分形图案构成方式是以四方连续构成为基础，通过对基本纹样的反复、对称、旋转以及色彩变化，塑造出形态丰富的分形图案。例如，图9是作者与5岁儿子利用分形图案进行的面料扎染，以连续排列或对称排列形成为面料纹样，从整体上看，各个基本单元排列规整，具有强烈的韵律感，而每个纹样本身又具有复杂细分化特征，使整个图案单纯但不单调，具有丰富的艺术美感。

图8 丝巾图案设计效果图

图9 面料扎染纹样设计

当然，在服装面料的印花图案设计中，设计者要根据消费者特征以及不同的产品用途展开设计，因为有的图案适合用于服装但不适合用于丝巾，而有些图案则适合用于丝巾而不适合用于服装，因此，必须要将产品用途作为分形图案设计的重要依据。另一方面，图案的色彩重要的视觉要素，也是吸引消费者的第一要素，这就需消服装面料的设计人员合理使用色彩，以塑造更为强烈的形式美感。

5 结语

分形是描述大自然重要数学工具，是现代科技领域的新型理论，在产生以来的几十年中已经迅速被应用于化学、物理、生物、材料等诸多学科领域。分形艺术图形作为分形理论指导下借助计算机技术塑造的图形，凭借其审美上的独特性被广泛应用于图案设计领域，并发挥出巨大的作用。同时，我们也应该认识到，分形图形的生成技术仍处于迅速发展期，在今后的图案设计领域必将拥有更大的发展空间。作为艺术设计师，必须要充分利用分形图形的市场和艺术价值，使其为服装面料等领域的图案设计服务。

[1] 夏伶俐，苏洁．分形图形在服装设计中的应用研究[J]．艺术与设计(理论)，2010，2(12)：245-247．

[2] 李雪霞．服饰图案的一朵奇葩——分形图[J]．中国制衣，2009，(02)：66-67．

[3] 黄俊敏，李响，杨兆麟．分形艺术在服饰设计中的应用[J]．浙江纺织服装职业技术学院学报，2007，(04)：19-22．

[4] 黄俊敏，李响，杨兆麟．分形艺术在服饰设计中的应用[J]．南通纺织职业技术学院学报，2007，(03)：23-26．

The Application of Fractal Theory in the Design of Clothing Printing Pattern

DOU Lin-xian

(College of Economic and Technical, Anhui Agricultural University, Hefei Anhui 230041, China)

Fractal graphics based on fractal theory can provide new means and ideas for clothing print pattern design, which has important theoretical significance and practical value. Based on the basic connotation of fractal theory, this paper first analyzes its feasibility in the design of clothing printing pattern, and then discusses in detail the composition form of clothing print pattern based on fractal theory and the practical application in the pattern design of clothing printing.

fractal theory; fractal graphics; clothing printing pattern

窦林贤（1983），女，讲师，硕士，研究方向：平面设计专业.

安徽省自然科学重点项目（KJ2017A817）.

J523.2

A

2095－414X(2018)03－0046－05