薄壁管涡流检测的不确定度评定

(中核武汉核电运行技术股份有限公司秦山分公司,海盐 314300)

在测量工作中,由于人们对其认识的不足、测量工具及测量过程控制的不完善，均会产生测量结果的不确定度。测量不确定度是表征被测量的真值所处的量值范围的一种评定方法。其是对测量结果受测量误差影响不确定程度的科学描述。具体地说，不确定度定量地表示了随机误差和未定系统误差的综合分布范围，可以近似地理解为一定置信概率下的误差限值[1-2]。

1 测量不确定度的原理

不确定度可以分为用统计学方法计算的A类标准不确定度uA，其可以用实验标准误差来表征，对随机变量x在相同条件下进行n次独立测量，n一般取10次，其测量结果的算术平均值为

(1)

第一阶贝塞尔函数

(2)

(3)

另一类是其他非统计学方法(或者说经验的方法)评定的B类标准不确定度uB，其信息来源有：以前的观测数据；对有关技术资料和测量仪器特性的了解和经验；生产部门提供的技术说明文件；校准证书、检定证书或其他文件提供的数据、准确度的等级或级别、误差限等；手册或某些资料给出的参考数据及不确定度；规定实验方法的国家标准或类似文件中给出的重复性限或复现性限。

(4)

在实际检测中，置信概率P通常取较大值，此时的不确定度称为扩展不确定度UX。常用标准不确定度的倍数表达，即

U=KuC

(5)

一般认定总的不确定度符合正态分布，即K取2，且对应不确定度分布为正态分布时，置信概率P约为95%。一般情况若不特别指明，不确定度均指扩展不确定度。

在涡流薄壁管材的检测技术中，影响检测结果不确定的因素很多，如涡流仪和涡流探头的性能、检测方法的选择、标定管的精度、填充系数的选择等都会对检测结果产生影响。另外，被检产品的缺陷性质、埋藏深度和缺陷走向也会对检测结果产生影响，下文分析薄壁管涡流检测时，对所测量缺陷的幅值、相位、伤深的不确定度方法的评定。

2 涡流检测缺陷幅值不确定度的评定

2.1 缺陷幅值不确定度的A类评定

所采用的设备与被检对象的名称及其参数如表1所示。

连接设备，系统设置后对被检薄壁管进行数据采集，最少采集10次。按表2和表3的参数调节数据。

表1 涡流检测设备一览表

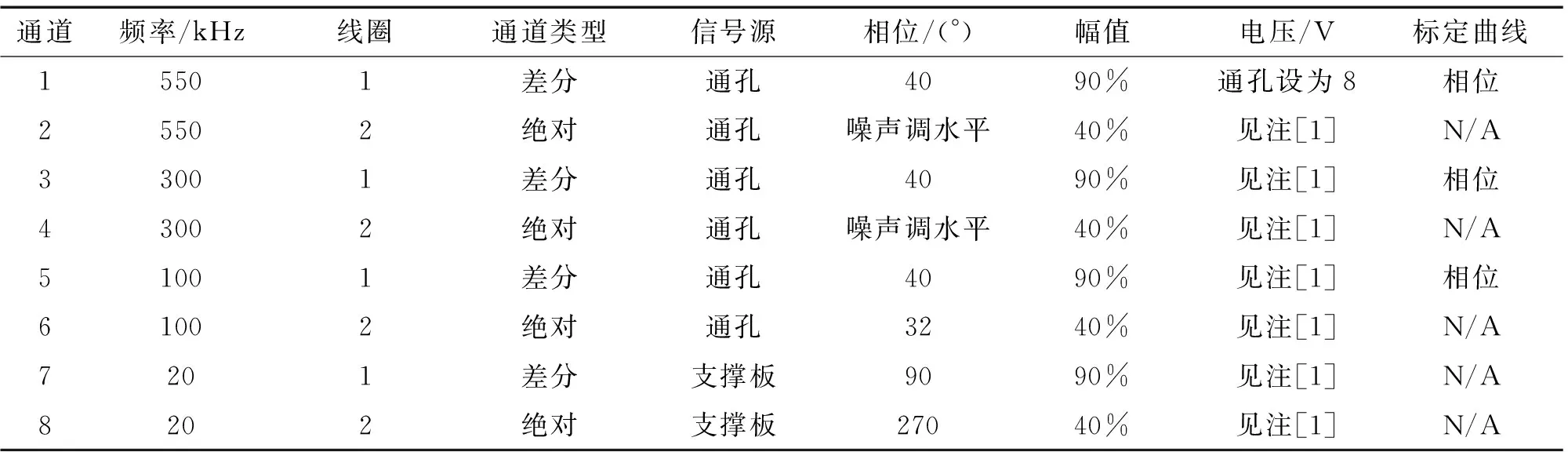
表2 缺陷幅值不确定度试验时的数据分析参数表

表3 缺陷幅值不确定度试验时的混频数据分析参数表

注：使用100%通孔,40%外伤和10%的外伤制作相位曲线。[1]指在将1通道的通孔信号电压设为8 V以后，将设置先保存到1通道，再归一化存储到其他各通道。

参数设置好后对φ1 mm的通孔用Vpp(多频涡流仪中测量幅值的一种方法)进行幅值测定，1～10通道的测试结果分别为8.01,7.98,8.07,7.94,8.02,8.02,8.01,8.03,8.02,7.96 V。由此，可得出10次测量的平均值=8.006 V。

根据贝塞尔公式得到单次试验的标准偏差为

其不确定度为

相对不确定度为

其自由度为

ν11=n-1=9

2.2 涡流检测缺陷幅值不确定度的B类评定

2.2.1 由标定管人工伤的尺寸公差引入的不确定度

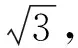
则由标定管引入的相对不确定度为

uB1=u1/1×100%=2.9%

估计ΔuB1/uB1=20%自由度(分子是分母的一个附加修正值，下同),则

2.2.2 由涡流仪电压值的幅度误差引入的不确定度

根据涡流仪的校准程序，其校准结果评价中对幅值的允许误差如表4所示。

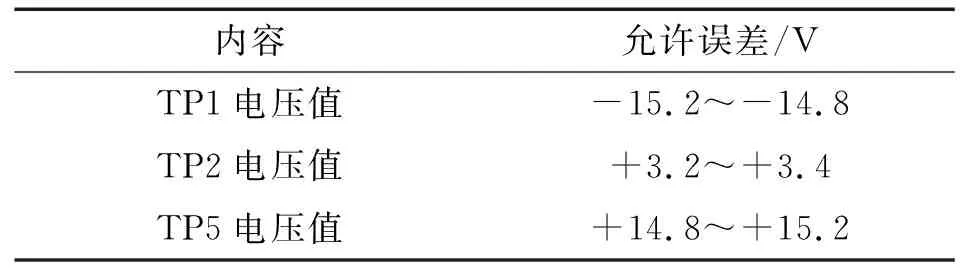
表4 涡流仪标准结果评价中的幅值允许误差

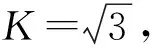
则由涡流仪电压引入的相对不确定度为

估计ΔuB2/uB2=20%自由度,则

2.2.3 由被检管子与检测线圈之间的填充系数的变化引入的不确定度

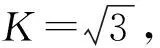
则由线圈与管径的填充系数的变化引起的相对不确定度为

估计ΔuB3/uB3=20%自由度，则

2.2.4 由人为测量误差引入的不确定度

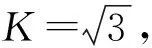
估计ΔuB4/uB4=20%自由度,则

2.2.5 B类不确定度的合成

2.3 涡流检测缺陷幅值的合成不确定度

合成不确定度为

自由度为

扩展不确定度为

U=KuC=2×4.06%=8.12% (K=2)

对涡流检测缺陷幅值的不确定度分析后进行汇总，结果如表5所示。

3 涡流检测缺陷相位不确定度的评定

3.1 涡流检测缺陷相位不确定度的A类评定

采用表1所示的设备及探头,对一直径为φ1 mm的通孔测量10次，其相位数值分别为40°，40°，40°，41°，40°，38°，40°，41°，40°，39°。由此，可得出10次测量的平均值=39.9°。

根据贝塞尔公式得到单次实验标准偏差为

表5 涡流检测缺陷幅值的不确定度汇总

其不确定度为

相对不确定度为

其自由度为

ν11=n-1=9

3.2 涡流检测缺陷相位不确定度的B类评定

3.2.1 由涡流仪测量公差引入的不确定度

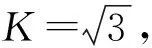
估计ΔuB1/uB1=20%自由度,则

3.2.2 因人为因素造成的测量不确定度

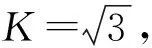
估计ΔuB2/uB2=20%自由度,则

3.2.3 B类不确定度的合成

3.3 涡流检测缺陷相位的合成不确定度

合成不确定度为

自由度为

扩展不确定度为

U=kuC=2×5.55%=11.1% (K=2)

对涡流检测缺陷相位的不确定度分析后进行汇总，结果如表6所示。

表6 涡流检测缺陷相位的不确定度汇总

4 涡流检测缺陷伤深不确定度的评定

4.1 涡流检测缺陷伤深不确定度的A类评定

采用表1中的设备及探头,对一相对于壁厚为41%的外环槽测量10次，其伤深数值分别为41%，41%，41%，42%，41%，40%，40%，42%，41%，40%。由此，可得出10次测量的平均值=40.9%。

根据贝塞尔公式得到单次试验标准偏差为

其不确定度为

相对不确定度为

其自由度为

ν11=n-1=9

4.2 涡流检测缺陷伤深不确定度的B类评定

4.2.1 由标定管人工伤尺寸公差引入的不确定度

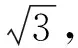
则由标定管引入的相对不确定度为

估计ΔuB1/uB1=20%自由度,则

4.2.2 因人为因素造成的测量不确定度

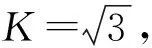
估计ΔuB2/uB2=20%自由度，则

4.2.3 B类不确定度的合成

4.3 涡流检测缺陷伤深的合成不确定度

合成不确定度

自由度为

扩展不确定度

U=KuC=2×1.62%=3.24%(K=2)

对涡流检测缺陷伤深的不确定度分析后进行汇总，结果如表7所示。

本节只从仪器和人为因素考虑了缺陷伤深的B类不确定度，而影响缺陷伤深检测结果不确定度的重要因素还有缺陷自身性质、走向等，由于缺陷自身影响的定量分析比较困难，故未计算其对伤深的不确定度贡献。

表7 涡流检测缺陷伤深的不确定度汇总

5 结语

涡流检测薄壁管对其缺陷的幅值测量不确定度为8.12%，自由度为31.15；对其相位的测量不确定度为11.1%，自由度为28.7；只考虑设备及人员对其缺陷的伤深测量不确定度为3.24%，自由度为19.44。参考上述数据，在薄壁管的涡流检测中，其参考管的初始标定，检测结束标定及中间标定时其幅值、相位、差值在10%以内为佳;在薄壁管的在役检测中，其缺陷的幅值、相位与最近一次检测数据比较，其相差在10%以内,则认为缺陷无显著变化。

参考文献:

[1] JJF 1059-1999 测量不确定度评定与表示[S].

[2] JJF 1001-2011 通用计量术语及定义[S].