不含4-圈和5-圈的平面图的非正常2-染色的一个新结果

周倩倩,孙磊

(山东师范大学数学与统计学院,山东 济南 250014)

1 引言

先定义一些概念,本文中所考虑的图是有限,简单,无向图.称图G=(V,E)是可平面的,如果它能被嵌入一个平面使得边仅在端点处相交.可平面图在平面内的一个嵌入叫平面图.对于平面图G,用V,E,F,∆,δ,分别表示平面图G的顶点集,边集,面集,最大度,最小度.对任意一个顶点v∈V,用d(v)表示v在G中的度数,即与v相关联的边的条数.如果相应地有d(v)=k,d(v)≥k,d(v)≤k,称v分别为k-点,k+-点,k−-点.对于面f∈F,用d(f)表示f的边界的长度,称为面f的度.称f分别为k-面,k+-面,k−-面,如果相应地有d(f)=k,d(f)≥k,d(f)≤k.一个k-圈是一个长度为k的圈,3-圈又叫作三角形.称两个圈邻接,若它们至少有一条公共边.令v∈V,称v为一个ij-点,若i≤d(v)≤j.一个图的围长指的是这个图中最短圈的长度.另外,图中的实点表示度数已经确定,虚点的度数尚未确定.更多的术语可见文献[1].

设d1,d2,···,dk是k个非负整数,若图G=(V,E)的顶点集V能被剖分成k个子集V1,···,Vk,使得对任意的i=1,···,k,Vi的点导出子图G[Vi]的最大度至多为di,则称图G是非正常 (d1,d2,···,dk)-可染的,简称 (d1,d2,···,dk)-可染的.用这个概念,著名的四色定理可叙述为:每个平面图是(0,0,0,0)-可染的,见文献[2-3].对于一个(d1,d2,d3)-可染的平面图,已有一些结果是通过禁掉某些圈,得到一些充分条件,见文献[4-5].而我们将目标转移到研究平面图非正常染色的最简单的形式,即用两种颜色来染平面图.另外还有许多文章研究围长g≥6,见文献[6-8].令ϑg表示围长至少为g的平面图类,文献[9]构造出一个在ϑ4中不能(d1,d2)-可染的图,而且在围长的限制下,有以下结果:

定理 1.1围长至少为5的平面图为(2,6),(4,4),(3,5)-可染的[6,10-11].

基于上述结果,我们将不再限制围长,而是禁掉4-圈和5-圈,保留3-圈,得到的主要结果如下:

定理 1.2既不含4-圈又不含5-圈的平面图是(9,9)-可染的.

2 定理1.2的证明

假设定理1.2不成立,设G=(V,E)为定理1.2的一个点极小反例.显然G是2-连通的,将G嵌入平面,得到一个平面图G=(V,E,F),其中F为G的面的集合.因为G中不含4-圈,所以G不含相邻三角形,我们先来研究G的结构特征.

2.1 结构分析

说正常染好一个点v是指用一个未曾用在v的任何邻点上的色去染v.对于一个图G=(d1,d2),令φ=1,2表示颜色集,若φ(v)=i,且v关联di个染颜色i的邻居,则称点v为一个i-饱和点.

引理 2.1δ(G)≥2.

证明假设G有一个1-点,由G的极小性,G-v有一个(9,9)-染色φ,因为v为1-点,所以v的邻点至多用了一种颜色,因此v可正常染好,从而得到G的一个(9,9)-染色,这与G的选取相矛盾.

引理 2.2每个18−-点至少有一个19+-邻点.

证明反证法.假设v为一个18−-点,且v的每个邻居的度至多为18,由G的极小性,G-v有一个(9,9)-染色φ=1,2,显然,v的邻居中两种颜色必须都出现,不然,很容易将G染回.不失一般性,若v至多9个邻居染2,则可先让v染2,若不能得到G的一个(9,9)-染色,则说明染2的v的邻居中至少有一个2-饱和点,重染这些2-饱和点为1,因为v的邻居的度都至多为18,所以可重染为1,这样v可染2,从而得到G的一个染色,矛盾.

引理 2.3若v为G的一个2-点,则v邻着一个11+-点,一个19+-点.

证明首先由文献[10]中的引理2.1可知,对于G=(9,9)中的二度点,此二度点邻着两个 11+-点,又由上面的引理 2.2可知,每个18−-点至少有一个19+-邻点,所以G的一个2-点,邻着一个11+-点,一个19+-点.

引理 2.4若v为G的一个3-点,则v至少邻着一个11+-点,一个19+-点.

证明首先由文献[10]中的引理2.2可知,对于G=(9,9)中的三度点,此三度点至少邻着两个11+-点,又由上面的引理2.2可知,每个18−-点至少有一个 19+-邻点,所以G的一个 3-点,至少邻着一个11+-点,一个19+-点.

引理 2.5每个19-点,至少有一个9+-邻点.

证明反证法.假设v为一个19-点,且v的每个邻居的度至多为8,由G的极小性,G-v有一个(9,9)-染色φ=1,2,显然,v的邻居中两种颜色必须都出现,不然,很容易将G染回.不失一般性,若v至少10个邻居染2,则可先让v染1,若不能得到G的一个(9,9)-染色,则说明染2的v的邻居中至少有一个2-饱和点,因为v的邻居的度都至多为8,所以不会出现1-饱和点,同样类似也不会出现2-饱和点,这样v可染好,从而得到G的一个染色,矛盾.

下面是将用到的两个简单的结果.

观察 2.1每个 6+-圈,至多邻⌊d(f)/2⌋个 2-点.

观察 2.2若v为G的一个2-点,则此2-点不会同时邻接3-圈和6-圈.

2.2 权转移

为完成定理1.2的证明,将利用上述性质通过权转移方法导出矛盾.

显然定理1.2的点极小反例G=(V,E,F)是2-连通的,因此G中每个面的边界是一个圈.定义初始权ch(x)=d(x)−4,x∈V∪F,由握手定理和欧拉公式|V(G)|−|E(G)|+|F(G)|=2,有

通过重新定义权转移法则,重新分配点和面的权,使对每个x∈V∪F,有ch′(x)≥0,则得矛盾,

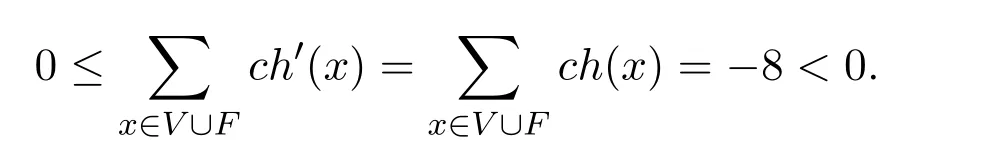
下面来证对每个x∈V∪F,ch′(x)≥0得到矛盾.权值转移规则如下:

(R1)每个 6+-面给它的每个3−-邻点

(R2)每个6-面给每个含2-度点的3-圈给每个不含2-度点的3-圈

(R3)每个7-面,若7-面中含有2-度点,且邻接3-圈,则给每个关联的3-圈若 7-面中不含有2-度点,且邻接3-圈,则给每个关联的3-圈

(R4)每个8+-面给每个关联的3-圈

(R5)每个1118-点v给每个关联的3−-点若v所关联的 3−-点的个数小于d(v)−1,则v将多余权值转移至所关联的67-面.

(R6)每个 19+-点给每个关联的3−-点

现在来验证对每个元素x∈V∪F,ch′(x)≥0.

v为G中任意一个点.

如果d(v)=2,显然ch(v)=−2.由前面的引理,v至少关联1个1118-点和1个19+-点,由 (R1),(R5),(R6)可得,

如果d(v)=3,显然ch(v)=−1.由前面的引理,v至少关联1个1118-点和1个19+-点,由 (R1),(R5),(R6)可得,

如果d(v)=410,显然ch′(v)≥0,因为由上述权转移规则,此类点既不接受权值也不给予权值.

如果d(v)=1118,最差的情况为11-点的情况.由前面的引理,v至少关联1个19+-点,由 (R5)可得,

如果d(v)=19,由前面的引理,v至少关联1个9+-点,由(R6)可得,

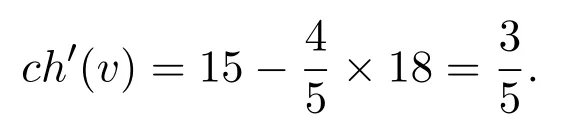
如果d(v)=20,由 (R6)可得,

如果d(v)≥21,最差的情况为21-点的情况.由(R6)可得,

f为G中任意一个圈,下面检验圈的权值.

如果d(f)=3,ch(f)=−1,下面分为两种情况讨论:

若3-圈中有2-点,根据前面观察1,则此3-圈至少邻接一个7+-面,一个6+-面,如图1中的(1).如果邻接7-面,则此7-面中含2-点,由(R2),(R3),(R4)可得,

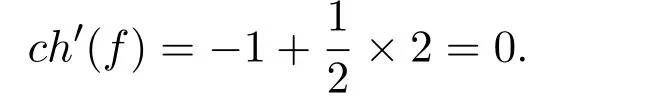
若3-圈中不含有2-点,则此3-圈至少邻接三个6+-面,则由(R2),(R3),(R4)可得,

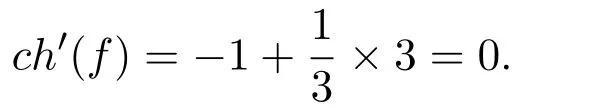
如果d(f)=6,ch(f)=2,最差的情况为邻接含有2-点的3-圈.

(a)邻接6个含2-点的3-圈,如图1中的(2),则由前面的引理,每个2-点所邻的度数较小的11+-点会至少邻接为2个19+-点,所以至少会多出的权值,由(R1),(R5)得,

(b)若邻接1个2-点,因为不含5-圈,最差的情况为邻接4个3-圈,如图1中的(3),则与 (1)类似,由(R1),(R5)得,

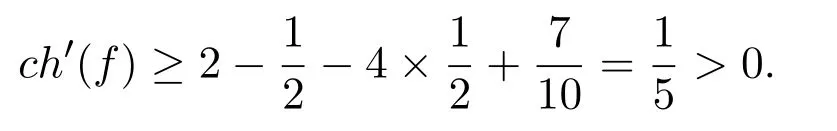
(c)若邻接 2个 2-点,因为不含 5-圈,最差的情况为邻接 2个 3-圈,如图 1中的 (4),由 (R1)得,

(d)若邻接3个 2-点,因为不含5-圈,由观察2,此时不邻接 3-圈,由(R1)得,

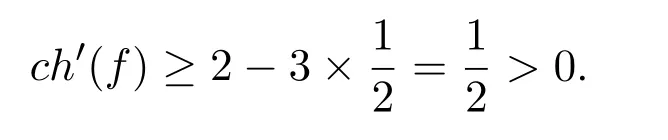
如果d(f)=7,ch(f)=3,类似于上述分析:

(a)邻接7个3-圈,这种情况下7-圈中无2-点,如图1中的(5),都为4+-点,则由 (R3)可得,

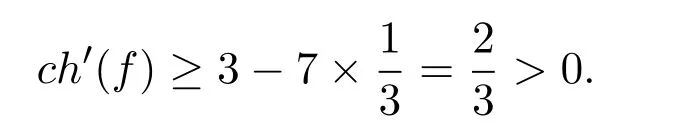
(b)若7-圈中含有2-点,类似于6-圈的分析,分为以下几种情况:

若邻接 1个 2-点,因为不含 5-圈,最差的情况为邻接 6个 3-圈,如图 1中的 (6),则由 (R1),(R5)得,

若邻接2个2-点,因为不含5-圈,最差的情况为邻接 4个3-圈,如图1中的(7),则由 (R1)可得,

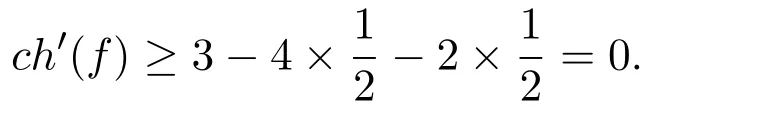
注 2.1因为不含4-圈和5-圈,所以不会同时出现两个及以上邻着2-点的3-圈.

若邻接 3个 2-点,因为不含 5-圈,最差的情况为邻接 2个 3-圈,如图 1中的 (8),则由 (R1)得,

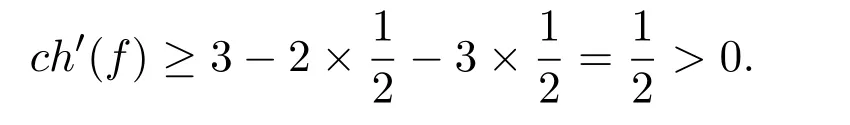
注 2.2类似于上述情况的说明,最差只能邻接1个3-圈.

如果d(f)=8,ch(f)=4,由前面的观察2可知至多邻4个2-点,又由(R1),(R4)可知,3-圈和2-点都会从8-圈中得到的权值,所以类似于上述分析,有

如果d(f)≥9,ch(f)≥5,由前面的观察 2可知至多邻⌊d(f)/2⌋个 2-点,根据注 2.1和注 2.2,且肯定邻接少于d(f)−⌊d(f)/2⌋个 3-圈,则由 (R1),(R4)可知即证.

于是移值后,在任何一种情况下,对每个元素x∈V(G)∪F(G),有ch′(x)≥0,所有点数值和这与矛盾,从而完成定理1.2的证明.

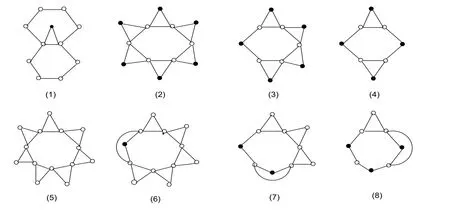
图1 圈的权值图

[1]Bollobas B.Modern Graph Theory[M].New York:Springer-Verlag,1998.

[2]Appel K,Haken W.Every planar graph map is four colorable part I:Discharging[J].Illinois J.Math.,1977,21:429-490.

[3]Appel K,Haken W.Every planar graph map is four colorable part II:Reducibility[J].Illinois J.Math.,1977,21:491-567.

[4]Xu L,Miao Z,Wang Y.Every planar graph with cycles of length neither 4 nor 5 is(1,1,0)-colorable[J].J.Comb.Optim.,2014(28):774-786.

[5]Hill O,Smith D,Wang Y,et al.Planar graphs without 4-cycles or 5-cycles are(3,0,0)-colorable[J].Discrete Mathematics,2013,313(20):2312-2317.

[6]Borodin O V,Kostochka A V.Defective 2-coloring of sparse graph[J].J.Combin.Theory Ser.B.,2014,104:72-80.

[7]Borodin O V,Kostochka A V,Yancey M.On 1-improper 2-coloring of sparse graphs[J].Discrete Mathematics,2013,313(22):2638-2649.

[8]Borodin O V,Kostochka A V.Vertex decompositions of sparse graphs into an independent set and a subgraph of maximum degree at most 1[J].Sibirsk.Mat.Zh,2011,52(5):1004-1010.

[9]Montassier M,Ochem P.Near-colorings:non-colorable graphs and np-completeness[J].The Electric Journal of Combinatorics,2015,22(1):1-57.

[10]Choi I,Raspaud A.Planar graphs with girth at least 5 are(3,5)-colorable[J].Discrete Mathematics.2015,338:661-667.

[11]Havet F,Sereni J S.Improper choosability of graphs and maximum average degree[J].J.Graph.Theory.2006,52:181-199.