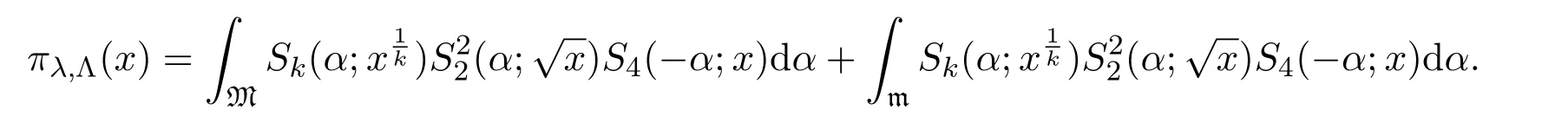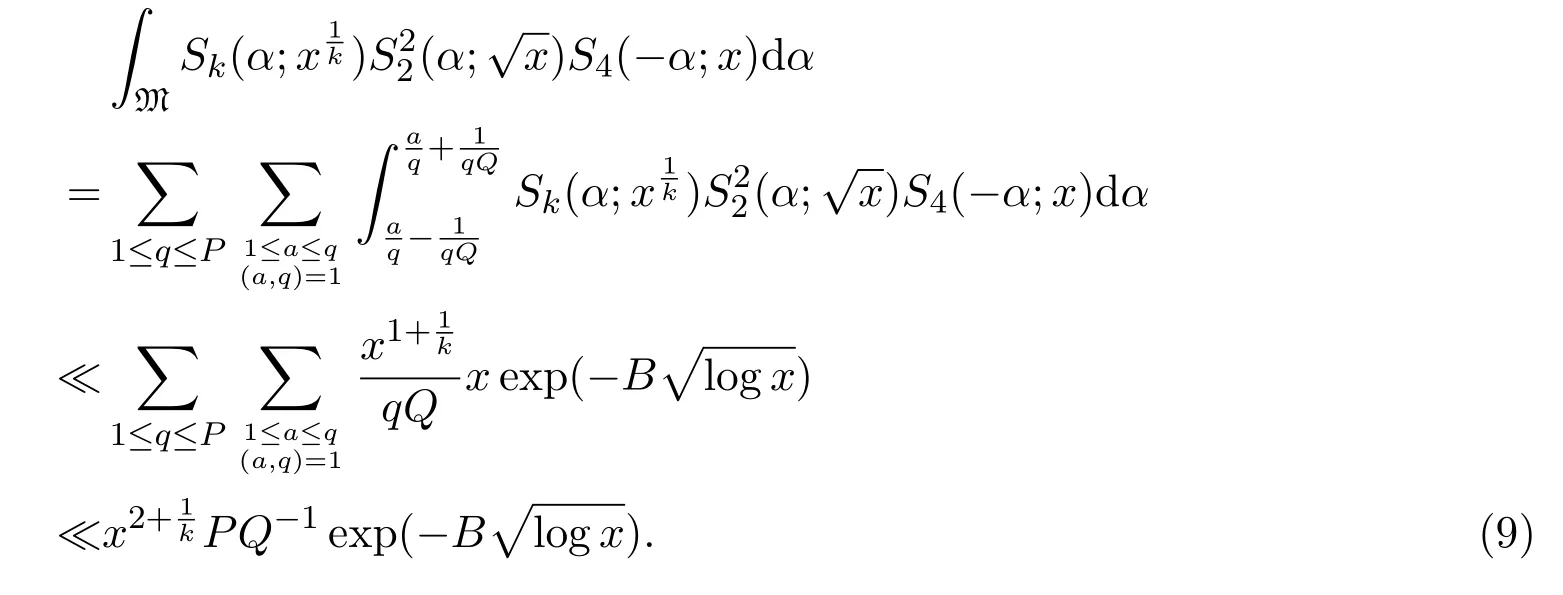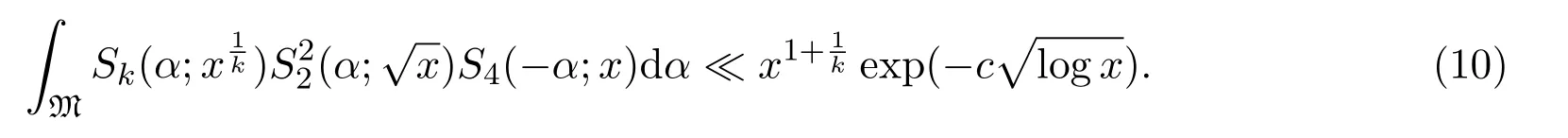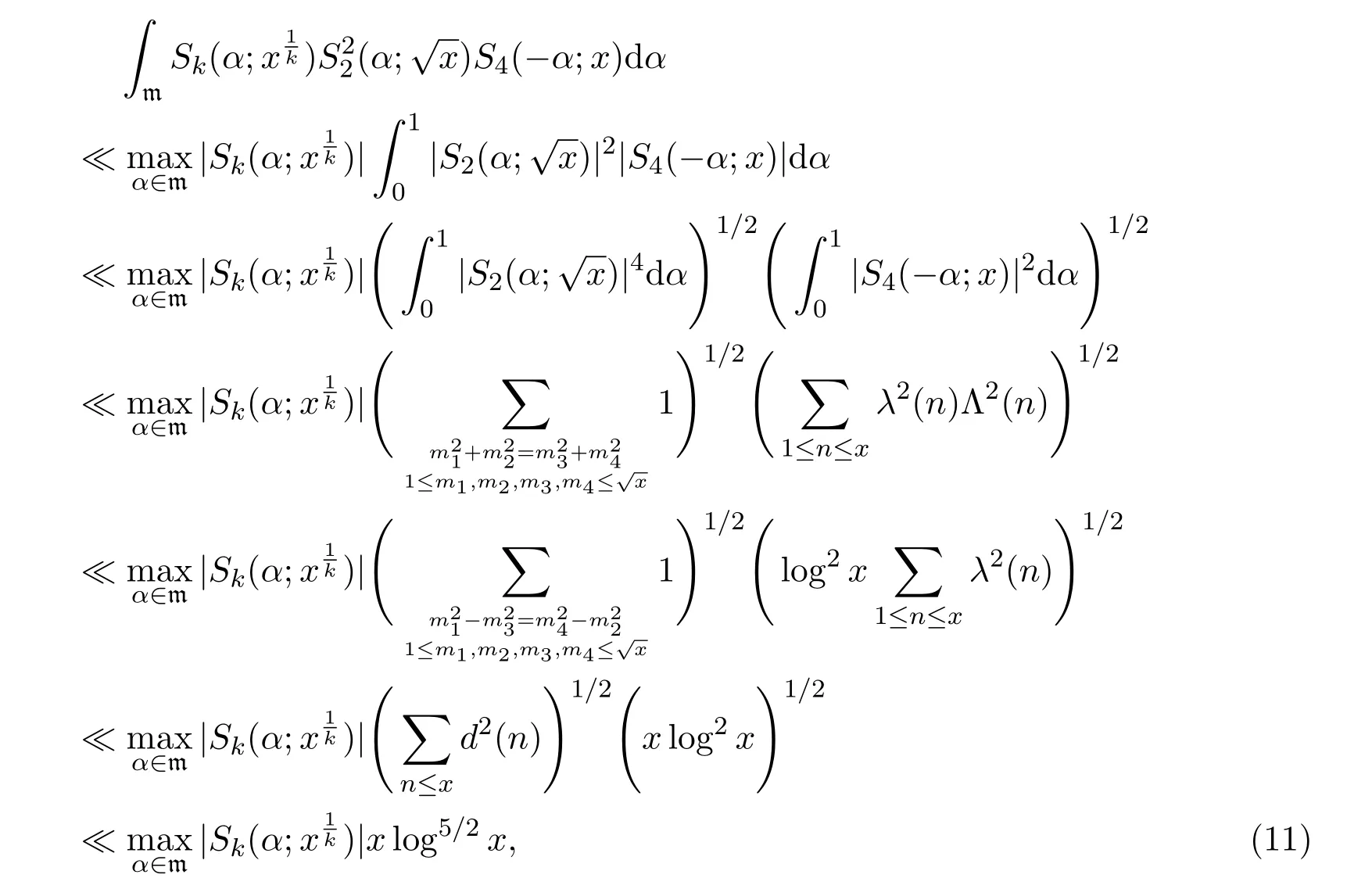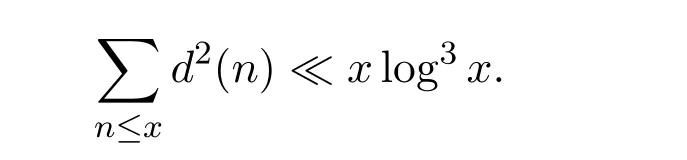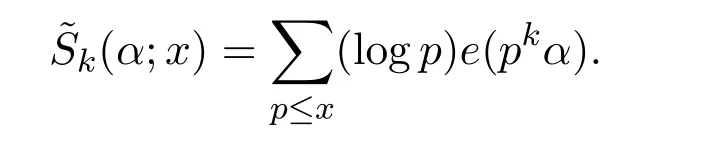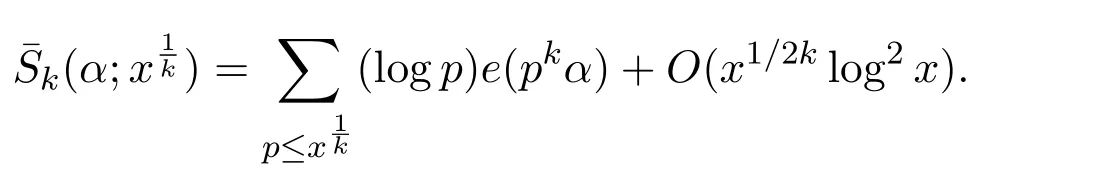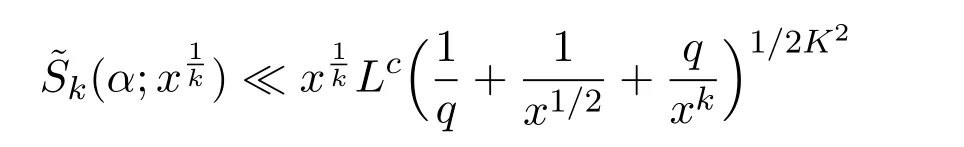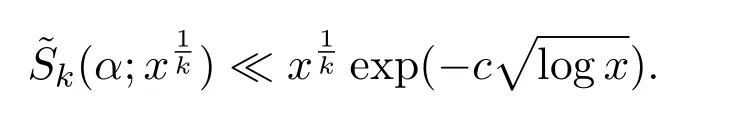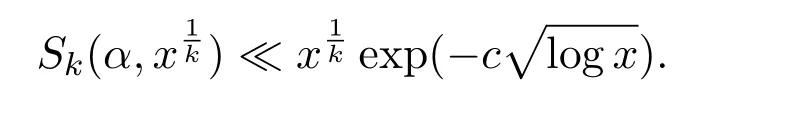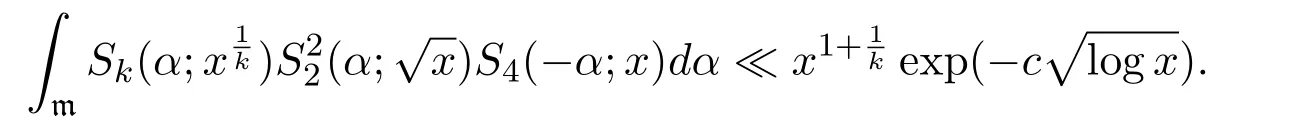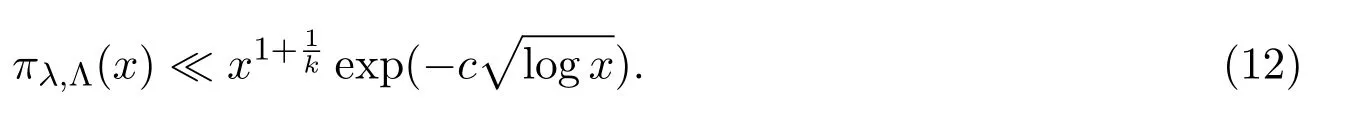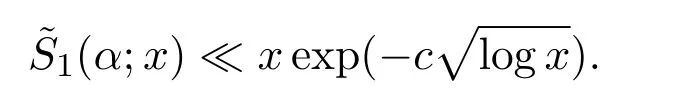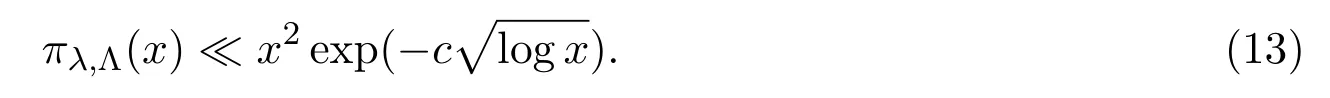A polynomial with prime variables attached to cusp forms
2018-06-23LiuDanLiuHuafengZhangDeyu
Liu Dan,Liu Huafeng,Zhang Deyu
(School of Mathematics and Statistics,Shandong Normal University,Ji′nan 250014,China)
1 Introduction
Letfbe a holomorphic cusp form for the group Γ=SL2(Z)of even integral weightk,with Fourier coefficientsa(n):
We normalizefwith the first coefficient being 1,and setλ(n)=a(n)/n(k−1)/2.From the Ramanujan conjecture it is easy to know that|λ(n)|≤d(n),whered(n)is the Dirichlet divisor function(this result is due to Deligne).
Many scholars are interested in researching the properties of quadratic forms.In 1963,Vinogradov[1]and Chen[2]independently studied the number of lattice points in the 3-dimensional balland showed the asymptotic formula
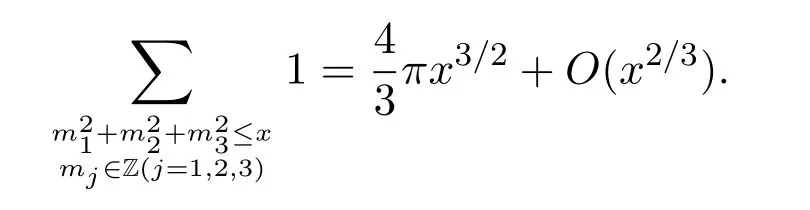
Subsequently,the exponent 2/3 in the above error term was improved to 29/44 by Chamizo and Iwaniec[3],and to 21/32 by Heath-Brown[4].Friedlander and Iwaniec[5]studied the number of prime vectors among integer lattice points in 3-dimensional ball.Letπ3(x)denote the number of integer points(m1,m2,m3)∈Z3withThey proved that
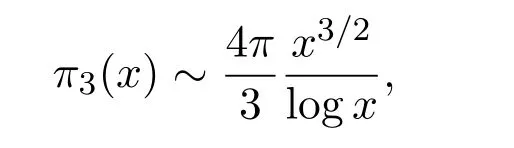
which can be viewed as a generalization of the prime number theorem.
Let Λ(n)stands for von Mangoldt function.Guo and Zhai[6]studied the asymptotic behavior of sum

and obtained for any fixed constantA>0,
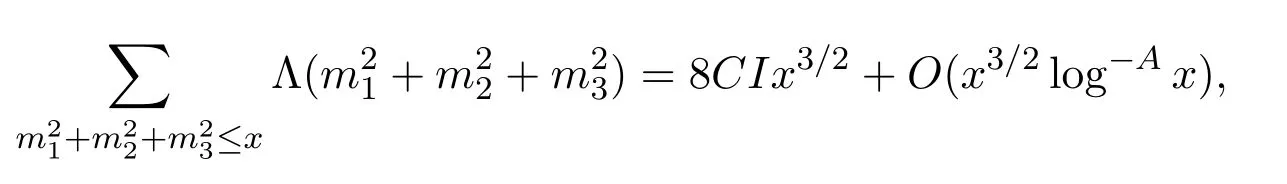
whereC,Iare computable constants.In 2015,Hu[7]studied the sum
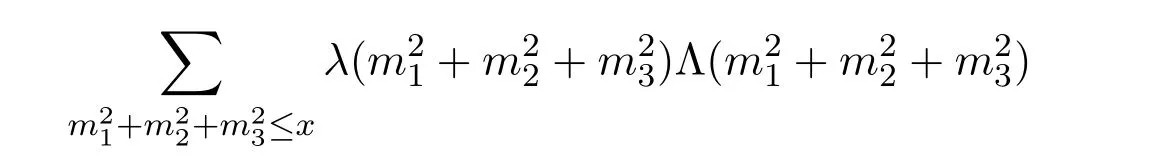
and obtained its upper boundx3/2logc1x,wherec1is a suitable constant.Later,G.Zaghloul[8]improved this result towherec2is arbitrary.Zhang and Wang[9]studied the sum
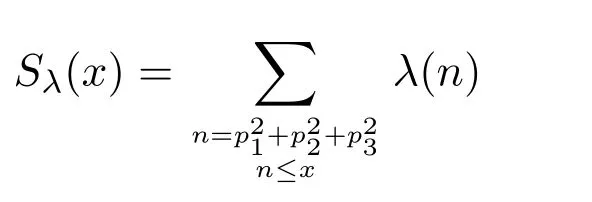
and proved
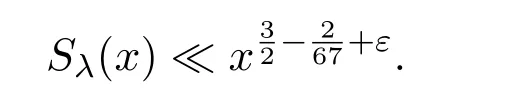
In 1938,Hua[10]established that almost alln≤Nsubject to the natural congruence conditions can be represented as the sum of two prime squares and akth power of prime,namely
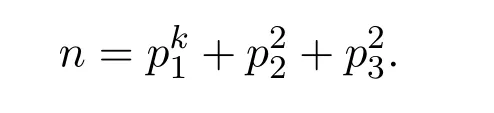
Later many results for the casek=1 were proved(see[8-9],[11-12]etc.).
In this paper,motivated by above results we firstly study hybrid problems of the Fourier coefficientsλ(n)and a polynomialand get the following results.
Theorem 1.1Let

Then we have
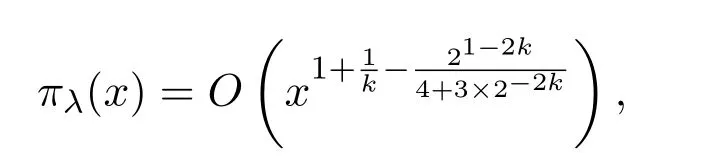
Theorem 1.2Let

Then we have

wherec>0 is arbitrary.
To prove our Theorems,we follow the classical line of the circle method,the di ff erence is that here we will deal with the sum
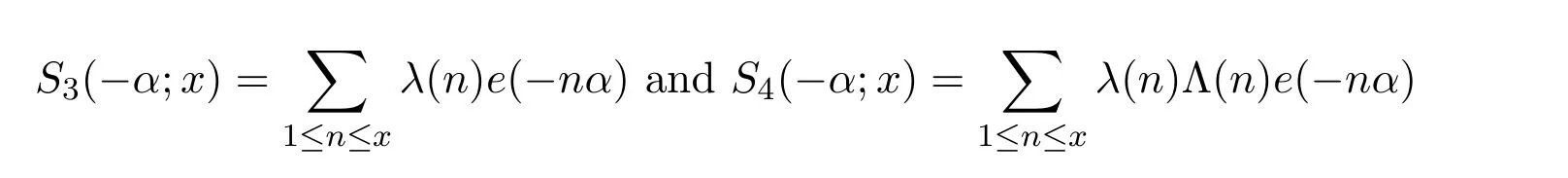
on the major arcs,which makes it difficult to establish the Voronoi′s summation formula ofλ(n)over the arithmetic progression.
Notation 1.1Throughout this paper,the lettercwith or without subscript denotes a constant,not necessarily the same in all occurrences.εdenotes an arbitrary positive real number.R,Z,N,P denotes the sets of all real numbers,integers,natural numbers and primes,respectively.As usual,we writee(z)for exp(2πiz).The letterp,with or without subscript,denotes a prime number.
2 Outline of circle method
Throughout this paper,xis a large positive integer andL=logx.For anyα∈Randy>1,de fine
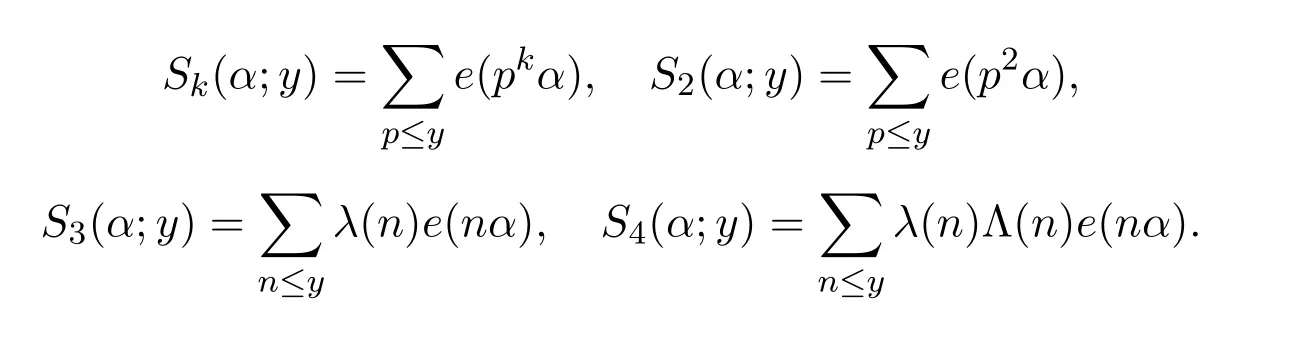
By the de finitions ofπλ(x),πλ,Λ(x)and the well-known identity
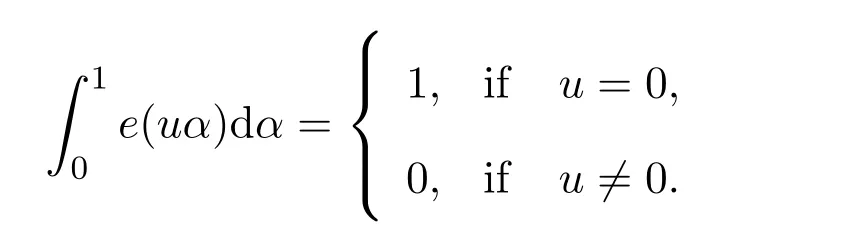
we have
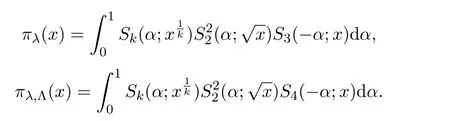
In order to apply the circle method,letP,Qare positive parameters,which will be decided later.By Dirichlet′s lemma on rational approximation,eachcan be written in the formfor some integersa,qwith 1≤a≤q≤Qand(a,q)=1.We de fine the major arcs M and the minor arcs m as follows:
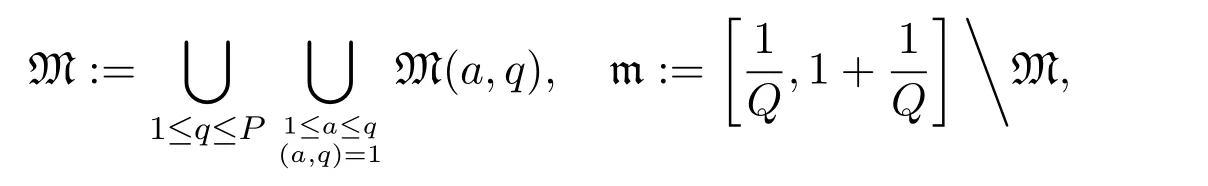
where

It follows from 2P≤Qthat M(a,q)are mutually disjoint.Then we can rewrite the integral from 0 to 1 as a sum of two integrals on the major arcs and the minor arcs,respectively.For example,we can rewriteπλ(x)as

Therefore,the problems are reduced to handle the integrals on the major arcs and the minor arcs.
3 Some lemmas
In this section,we give some lemmas which will be used in the proof of our theorems.
Lemma 3.1Supposeα∈M.Then,
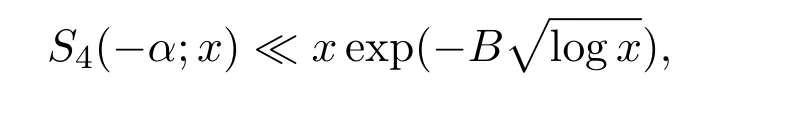
whereB>0 is a suitable positive constant.
ProofThis is lemma 3.4 in[8].
Lemma 3.2 Supposeα∈m.Let
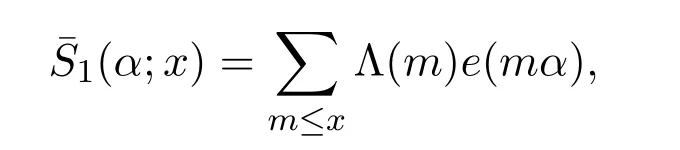
Then

ProofThis is well-known result of Vinogradov,which can be found in[12].
Lemma 3.3Supposeα∈m.Fork≥2,and setK=2k−1.Let
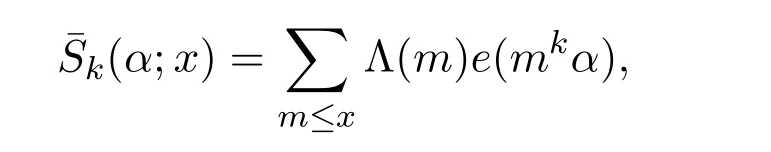
Then
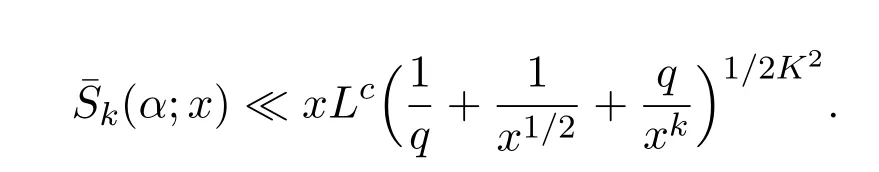
ProofThis is Harman′s result which can be found in[13].
Lemma 3.4Let
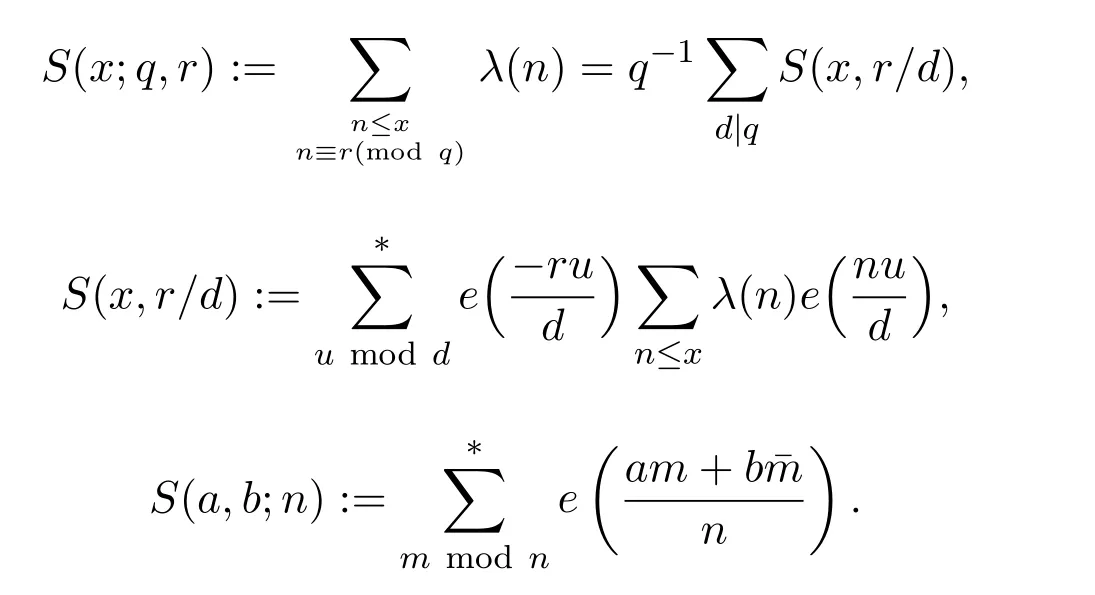
For anyf∈Hkand anyε>0,we have
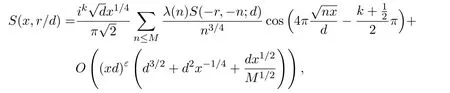
uniformly for 2≤M≤x.
Moreover,for any positive integerr,
ProofThis is Theorem 3.1 in[9].
4 Proof of Theorem 1.1
In this section,we prove Theorem 1.1.To do this,we need the estimate ofλ(n)over the arithematic progressions.
Recall the de finition of Kloosterman sum,we have

Noting that(a,q)=1,we can know that the inner sum isqifd=qandu−a≡0 modq.Otherwise the inner sum is 0.Therefore,

Let
By Lemma 3.4 and(1),we have that forx≥q,
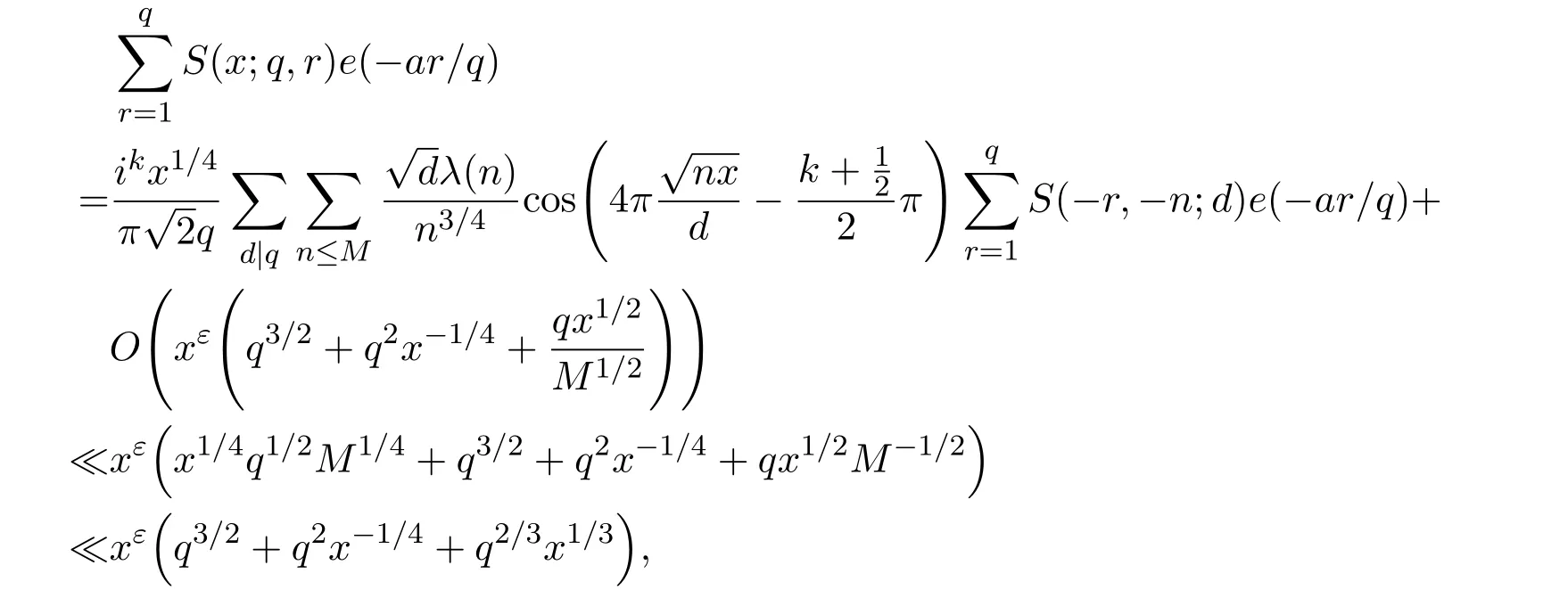
where we takeM=q2/3x1/3.Ifx uniformly forx>0.De fine IfT≪q,thenH(T;q,a)≪q1+εT.Ifq≪T,consider the integralApplying(1)and Lemma 3.3 withM=U,we obtain So,by a splitting argument,we have Supposeα=a/q+βwithWe can get We use the Abel′s summation and Lemma 3.4 to get By partial integration twice and then using(2)and(3)we have noting thatx=QP,andqsatis fiesq≤Pon the major arcs. Next,we prove the Theorem 1.1.We first handle the casek≥2.It is enough to take By the trivial estimates ofand(4),we have where we use Next,we estimate the contribution from the integral on the minor arcs.By Cauchy′s inequality,we obtain We also have whereK=2k−1. By partial summation formula,we have whereK=2k−1. Inserting this into(6),we can get that Combing(5)and(7),we can get Thus,we can get the desired bound of Theorem 1.1.Fork=1,we use Lemma 3.2 instead of Lemma 3.3 and takeP=x4/19,Q=x5/19.Then following a similar argument ofk≥2,we can get It is easy to verify In this section,we give the proof of Theorem 1.2.To do this,we can set whereCis a positive constant.Similarly,we can writeπλ,Λ(x)as a sum of two integrals i.e. Now we deal with the casek≥2.We first treat the integral on the major arcs.Using the trivial estimates ofand lemma 3.1,we have RecallingPandQare de fined by(8),we get Next,we estimate the contribution from the integral on the minor arcs.Using Cauchy′s inequality,we have where we have used the well-known estimate For the estimate ofwe use the following result. Lemma 5.1Supposeα∈m.Fork≥2,let Then ProofWe can easily get From Lemma 3.3,we have Noting thatP Combing these three formulas above,we have By partial summation formula and Lemma 3.1,we can easily get Inserting this into(11),we can get that From(9)and(10),we have Fork=1,using Lemma 3.2 and following Lemma 3.1,we can get Then,following the ideal ofk≥2,we can also get Combing(12)and(13),we complete the proof of Theorem 2.2. Reference [1]Vinogradov I M.On the number of interger points in a sphere[J].Izv.Akad.Nauk SSSR.Ser.Mat.,1963,27:957-968. [2]Chen J.Improvement of asymptotic formulas for the number of lattice points in a region of three dimensions(II)[J].Sci.Sinica,1963,12:751-764. [3]Chamizo F,Iwaniec H.On the sphere problem[J].Rev.Mat.Iberoamer,1995,11:417-429. [4]Heath-Brown D R.Lattice points in the sphere[J].Number Theory in Progress,1999,2:883-892. [5]Friedlander J B,Iwaniec H.Hyperbolic prime number theorem[J].Acta Math.,2009,202:1-19. [6]Guo R T,Zhai W G.Some problem about the ternary quadratic form[J].Acta Arith.,2012,156:101-121. [7]Hu L Q.Quadratic forms connected with Fourier coefficients of Maass cusp forms[J].Front.Math.China,2015,10:1101-1112. [8]Zaghloul G.Quadratic forms connected with Fourier coefficients of holomorphic and Maass cusp forms[J].J.Number Theory,2016,167:118-127. [9]Zhang D Y,Wang Y N.Ternary quadratic form with prime variables attached to Fourier coefficients of holomorphic cusp form[J].Journal of Number Theory,2017,176:211-225. [10]Hua L K.Some results in the additive prime number theory[J].Quart.J.Math.(Oxford),1938,9:68-80. [11]Bauer C,Liu M C,Liu J Y.On a sum of three prime squares[J].J.Number Theory,2000,85:336-359. [12]Liu J Y,Zhan T.New developments in the Addictive Theory of Prime Numbers[M].Singapore,World Scienti fic:2012. [13]Harman G.Trigonometric sums over primes(I)[J].Mathematika,1981,28:249-254.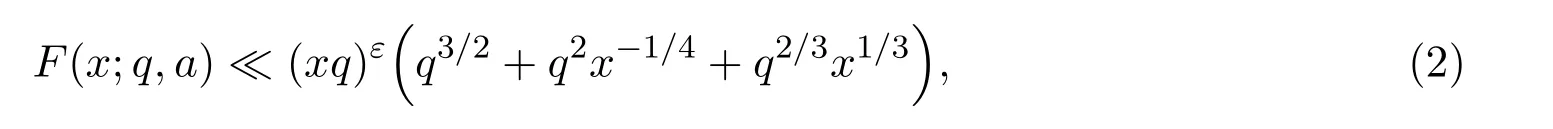
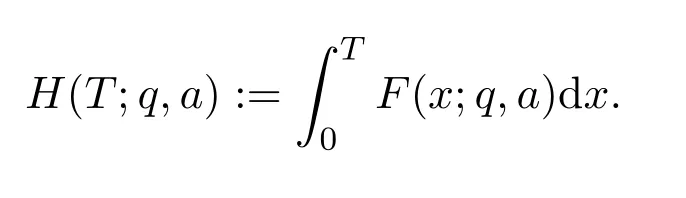
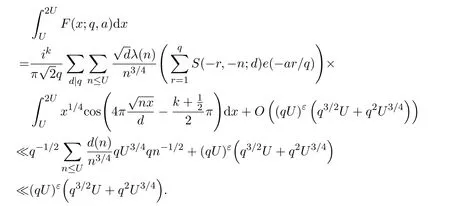
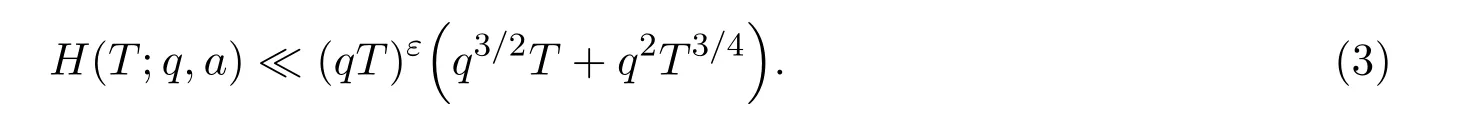
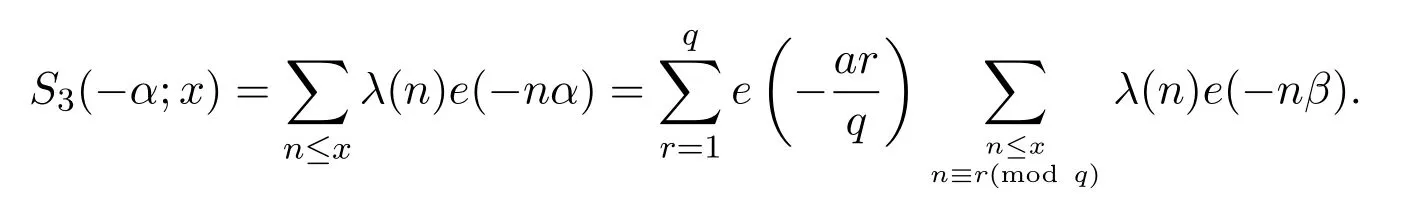
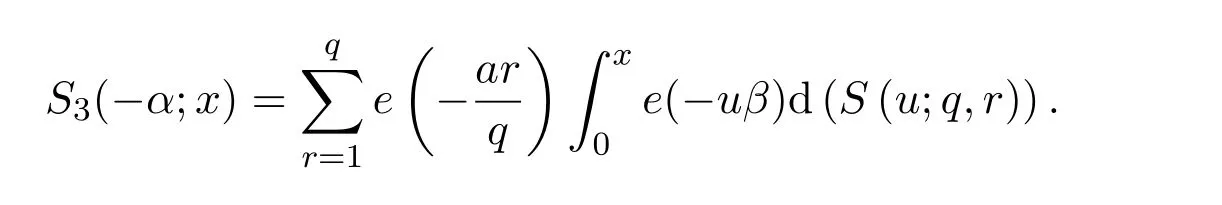
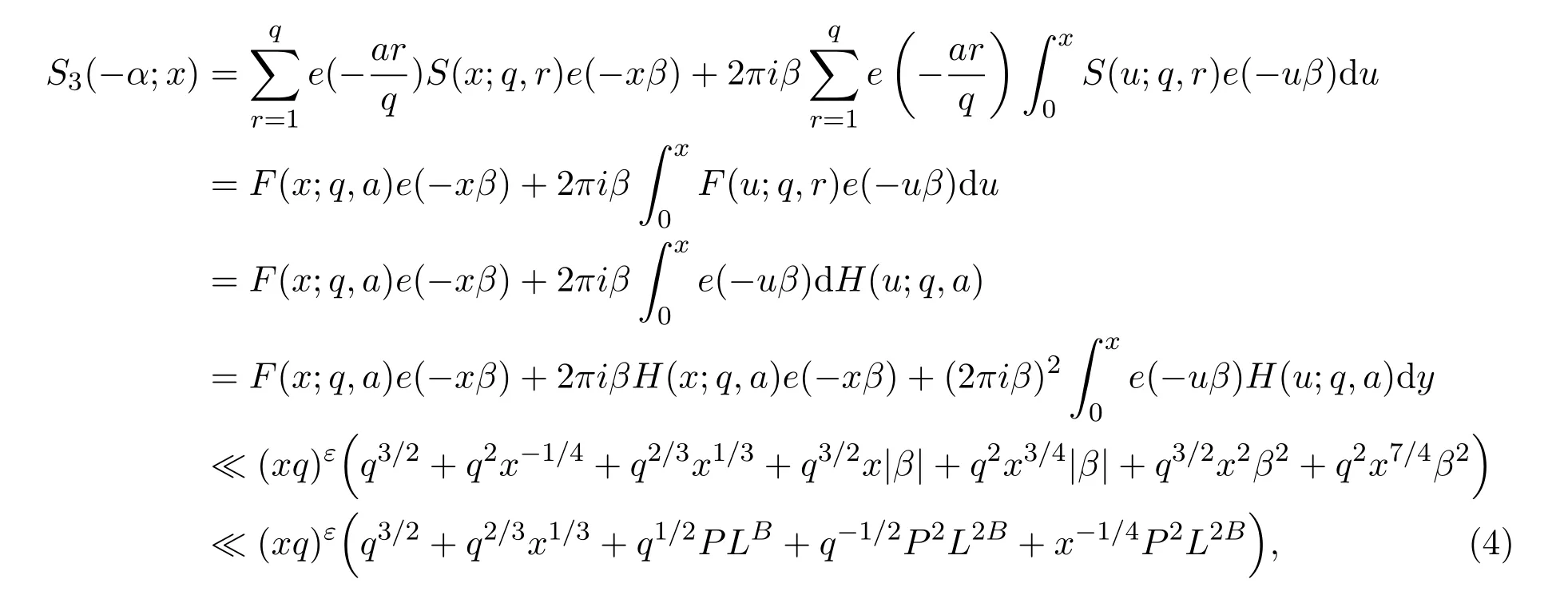
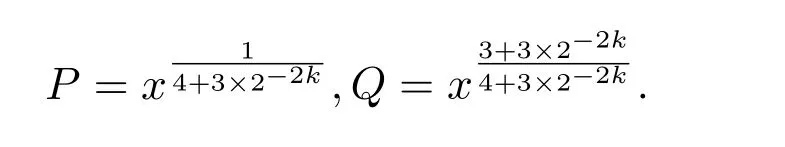
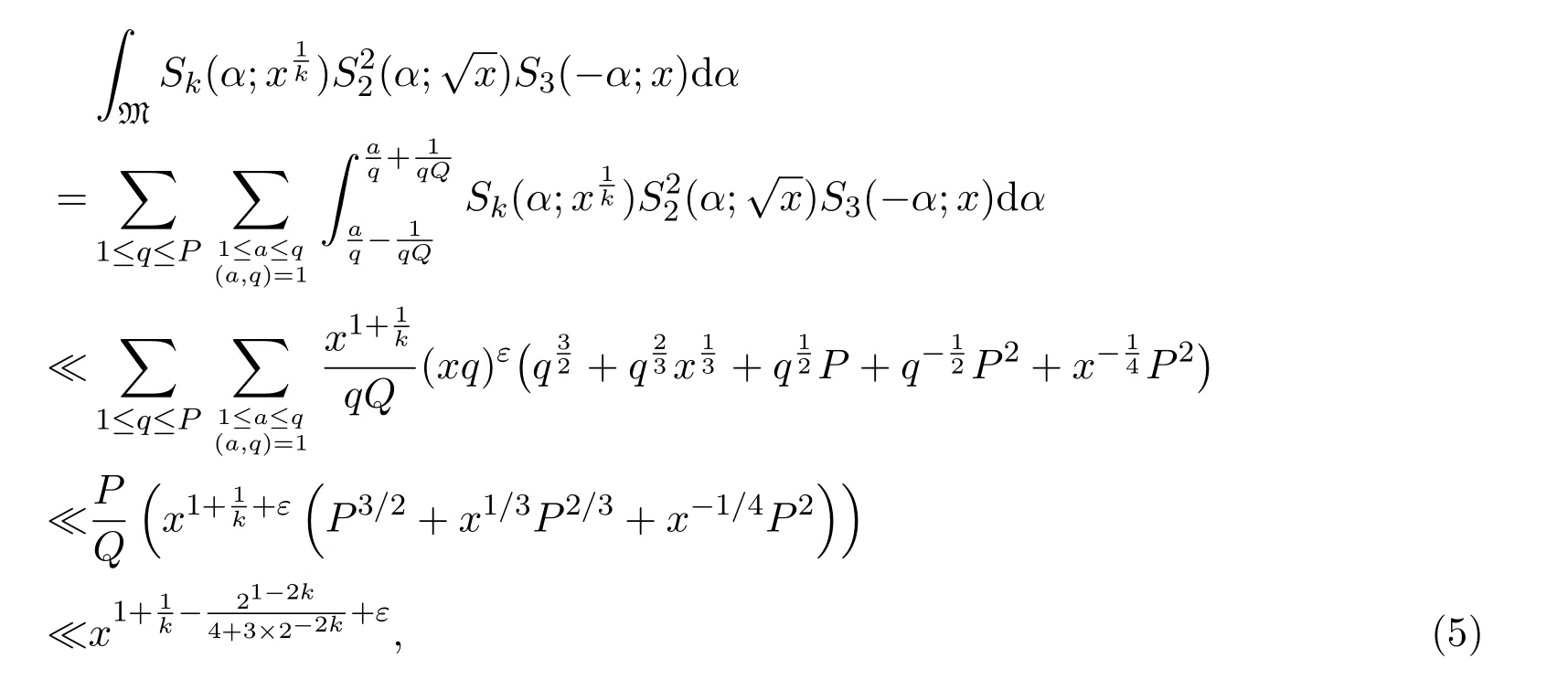
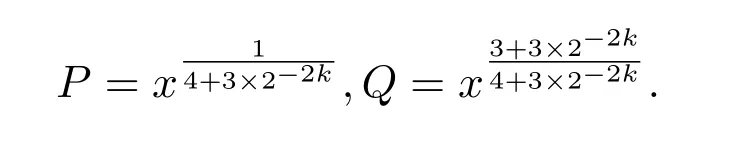
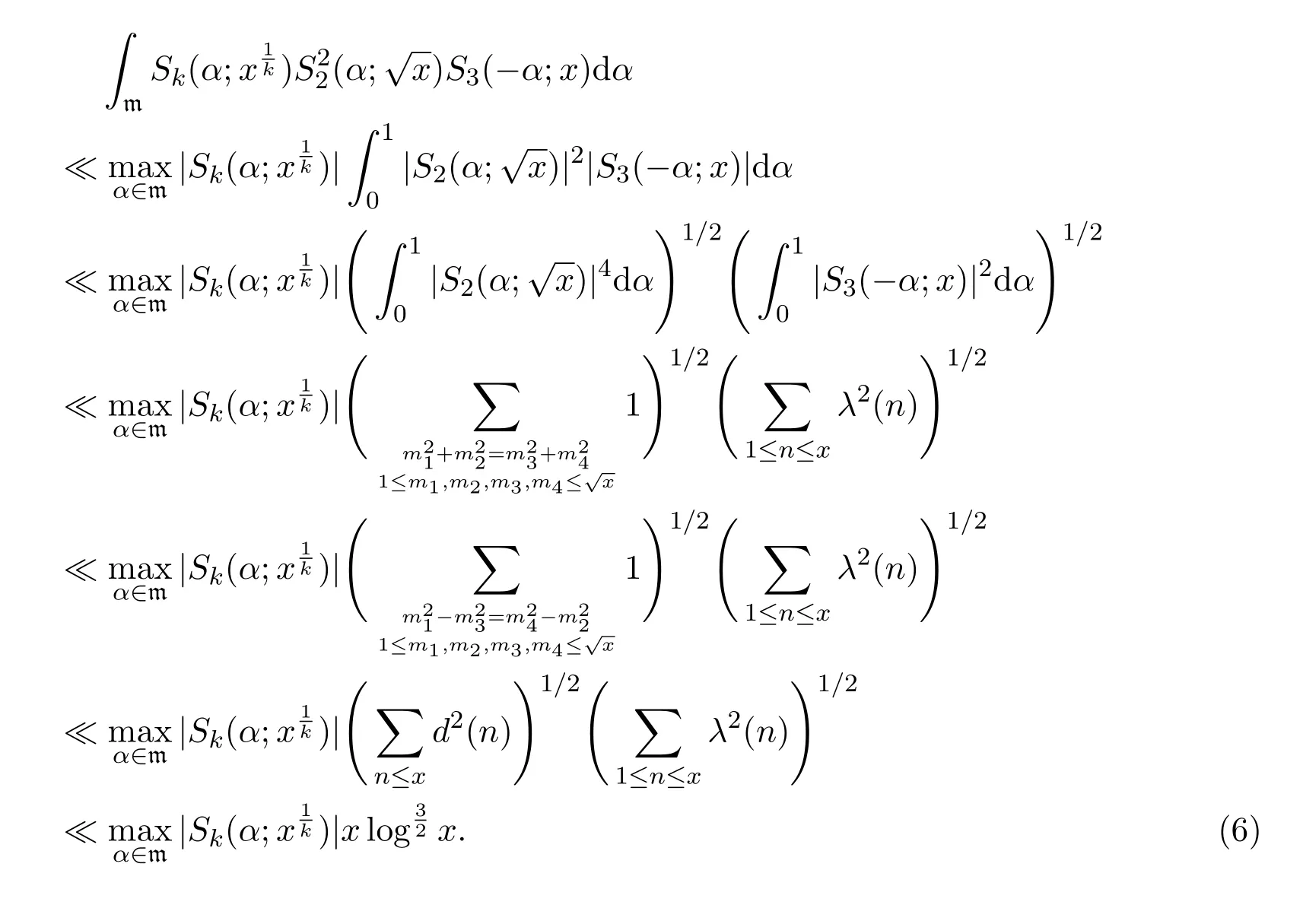

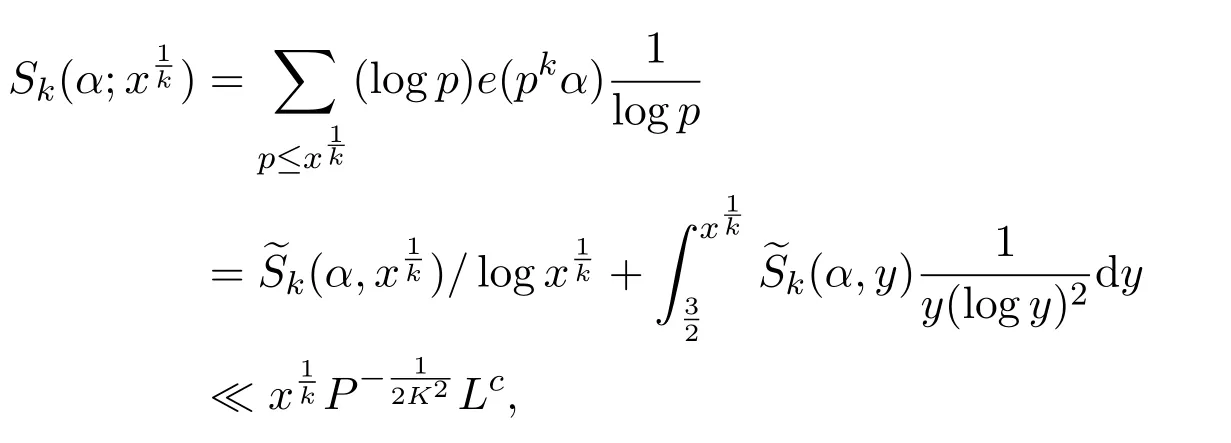
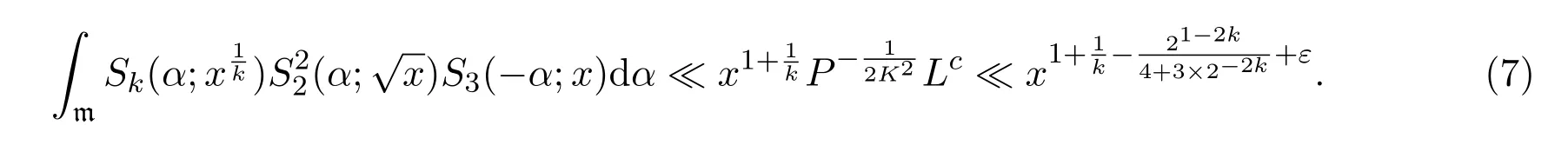
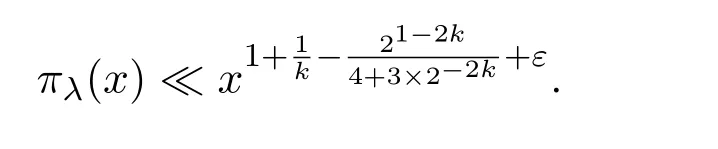
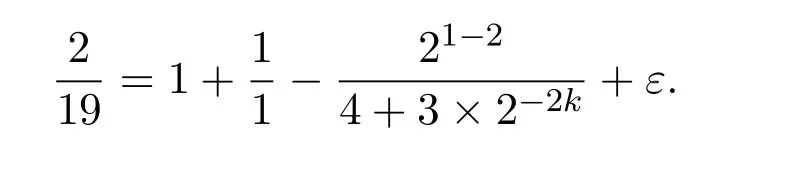
5 Proof of Theorem 1.2