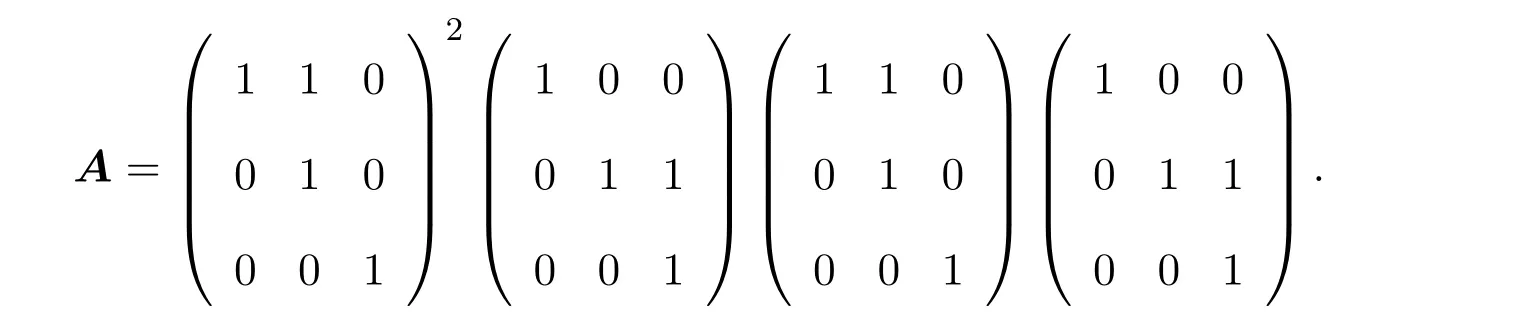三阶单位上三角非负矩阵
2018-06-23骆莉芳陈益智陈燕梅
骆莉芳 陈益智 陈燕梅
(1.华南师范大学数学科学学院,广东 广州 510006;2.惠州学院数学与大数据学院,广东 惠州 516007)
1 引言
由于上三角非负矩阵的行列式很容易计算得出,也可以化为Normal Hermite形式,所以上三角非负矩阵从而被广泛地研究,其相关研究成果读者可参考文献[1-8].在上三角非负矩阵的研究中,单位上三角非负矩阵已成为其研究的一个重要对象,能否将其分解成一些原子矩阵的乘积,并且在求得其最小的原子因式分解长度中起着非常重要的作用[1].关于非负矩阵因式分解的问题最早是文献[2]在1963年开始研究的.文献[3]和文献[4-5]分别研究了矩阵半群的因式分解问题.文献[6]把矩阵的因式分解理论应用到了整数值矩阵半群中,给出了这类矩阵的一些重要性质,并探讨了这类矩阵在什么意义下是可以唯一分解的,同时他们还提出了6个公开问题,有待进一步的解决.文献[7-8]主要研究三阶及n阶上三角非负矩阵半群的分解,并且部分解决了文献[6]中的公开问题1-问题4.本文将继续探究三阶上三角非负矩阵.
类似于文献[6-7],下面对本文所涉及到的预备知识进行介绍.
设N是一个正整数集,N0=N∪{0},用T3(N0)表示N0上的由所有行列式大于零的3阶上三角非负矩阵所构成的矩阵半群.对于本文出现而未提及的概念及术语,读者可参考文献[6-8].
定义 1.1[1]若S是一个含单位矩阵I的矩阵半群.对于A∈S,
(1)若存在B∈S使得AB=BA=I成立,则称A为S的一个单位.
(2)若A不是S的单位,由A=BC可推出B或C是S上的一个单位,则称A为S的一个原子.
(3)若S上的每个非单位元素都可以分解成S上一些原子的乘积,则将S称为原子半群.
定义 1.2[1]如果S是一个原子半群,A为S上任意的非单位元素.记
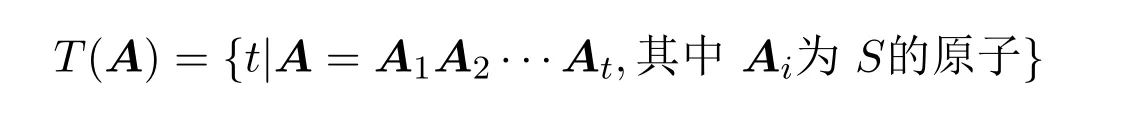
为A的原子因式分解长度集,用它来表示A在S中可以有限分解成一系列原子矩阵的乘积形式的一切可能的分解长度的集合.记l(A)=min{T(A)}表示A的最小的原子因式分解长度.
2 三阶单位上三角非负矩阵
2.1 最小的原子因式分解长度
引理 2.1[1]设S为T3(N0)中所有单位上三角非负矩阵所构成的矩阵半群,则任意的A∈S是原子当且仅当A=Xij=I3+Eij(1 借助上述引理,下面将介绍本文最主要的结果,即 定理 2.1记S为T3(N0)中所有三阶单位上三角非负矩阵所构成的矩阵半群,则对任意的 (1)当c≤ab时,有l(A)=a+b;(2)当c>ab时,有l(A)=a+b+c−ab. 证明由单位上三角非负矩阵的原子因式分解中原子矩阵类型是X12或X13或X23知, 从而X12和X13的乘积可以交换,X23和X13的乘积也可以交换,而X12和X13的乘积不可以交换.于是,A的任一因式分解必具有如下分解形式: 其中,c′,ai,bi∈N0,i=1,2,···,m. 这里, 注意到A的原子因式分解长度为 从而0≤c且c′∈N0,那么根据最小数原理可得,c′的最小值是存在的.因此,若要计算l(A),只需计算出c′的最小值便可.即若存在一组特解使得c′取得最小值,记该最小值为m,则可得到 由于对于任意的A∈S,其上三角元素a,b,c之间仅包含了下列三种数量关系,即c=ab或c>ab或c (I)当c=ab时,在(2)式中可取一组特解使得c′=0.而 0≤c′≤c,则c′的最小值为m=0.从而得到A的最小原子因式分解长度为l(A)=a+b. (II)当c>ab时,由于 则c−ab≤c′≤c.从而在(2)式中可取一组特解使得c′=c−ab.则c′的最小值为m=c−ab,则A的最小原子因式分解长度为 (III)当c 情形1当c (i)当a≥b时,有a≥c,在(2)式中可取一组特解 使得c′=0,则c′的最小值为m=0,从而A的最小原子因式分解长度为l(A)=a+b. (ii)当a 使c′=0,则c′的最小值为m=0,从而A的最小原子因式分解长度为l(A)=a+b. 所以当c 情形 2当 max{a,b} (i)当a≥b时,在(2)式中可取一组特解 其中,i∈{2,3,···,k−1,k+1,k+2,···,b−1},且 []表示取整符号.使得c′=0.则c′的最小值为m=0,从而A的最小原子因式分解长度为 (ii)当a 其中,i∈{2,3,···,k,k+2,···,a−1},使得c′=0.则c′的最小值为m=0,从而A的最小原子因式分解长度为l(A)=a+b. 所以当max{a,b} 综上所述,对任意单位上三角非负矩阵A,当c≤ab,有l(A)=a+b;当c>ab时,有 注2.1文献[8]中只是得出部分单位上三角非负矩阵的最小原子因式分解长度,而本文中的定理2.1针对T3(N0)中的单位上三角矩阵半群中的任意矩阵A,都给出了计算A的最小原子因式分解长度l(A)的公式,并且证明方法也不同于文献[8],从而完善了文献[8]中相应的结论. 特别地,在定理2.1的证明过程中,若将各情形下的特解代入分解式(1)中,便可得到全部的单位上三角非负矩阵A的其中一个具有最小的原子因式分解长度的分解. 定理 2.2记S为T3(N0)中所有三阶单位上三角非负矩阵所构成的矩阵半群,则对于任意的 (1)当c=ab时,A的其中一个具有最小的原子因式分解长度的分解为: (2)当c>ab时,A的最小原子因式分解长度为l(A)=a+b+c−ab,且A的其中一个具有最小的原子因式分解长度的分解为: (3)当c (i)若a≥b,则A的其中一个具有最小的原子因式分解长度的分解为: (ii)若a (4)当max{a,b} (i)若a≥b,则A的其中一个具有最小的原子因式分解长度的分解为: 其中 (ii)若a 其中 注 2.2定理2.2分情形详细探讨了三阶单位上三角非负矩阵A具有最小原子因式分解长度的其中一种分解. 对于任意的三阶单位上三角非负矩阵下面将针对定理2.1中的其中一个情形,即max{a,b} 例2.1设由于a=3,b=2,c=5,根据定理2.1,得到max{a,b} [1]Halava V,Harju T.On Markov′s undecidability theorem for integer matrices[J].Semigroup Forum,2007,75:173-180. [2]Cohn P M.Noncommutative unique factorization domains[J].Trans.Am.Math.Soc.,1963,109:313-331. [3]Jacobsom B.Matrix number theory.An example of nonunique factorization[J].Am.Math.Mon.,1965,72:399-402. [4]Chuan J C,Chuan W F.Factorizations in a semigroup of integral matrices[J].Linear Multilinear Algebra,1985,18:213-223. [5]Chuan J C,Chuan W F.Factorability of positive-integral matrices of prime determinants[J].Bull.Inst.Math.,Acad.Sin.,1986,14,1986:11-20. [6]Baeth N,Ponmarenko V,Adams,et al.Number theory of matrix semigroups[J].Linear Algebra Appl.,2011,434:694-711. [7]陈益智.半环上矩阵的若干研究[D].西安:西北大学图书馆,2012. [8]Chen Y Z.On factorizations of upper triangular nonnegative matrices of order three[J].Discrete Dynamics in Nature and Society,Volume 2015:Article ID 960182,6 pages.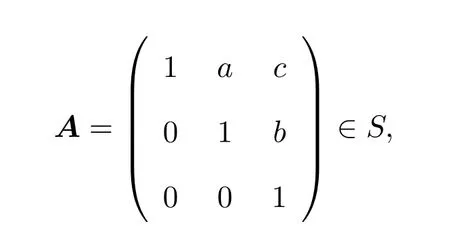
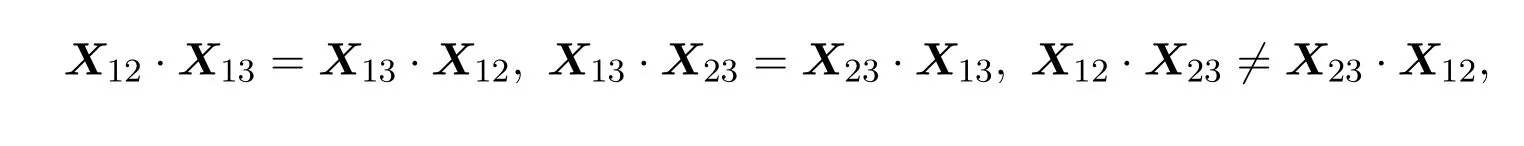
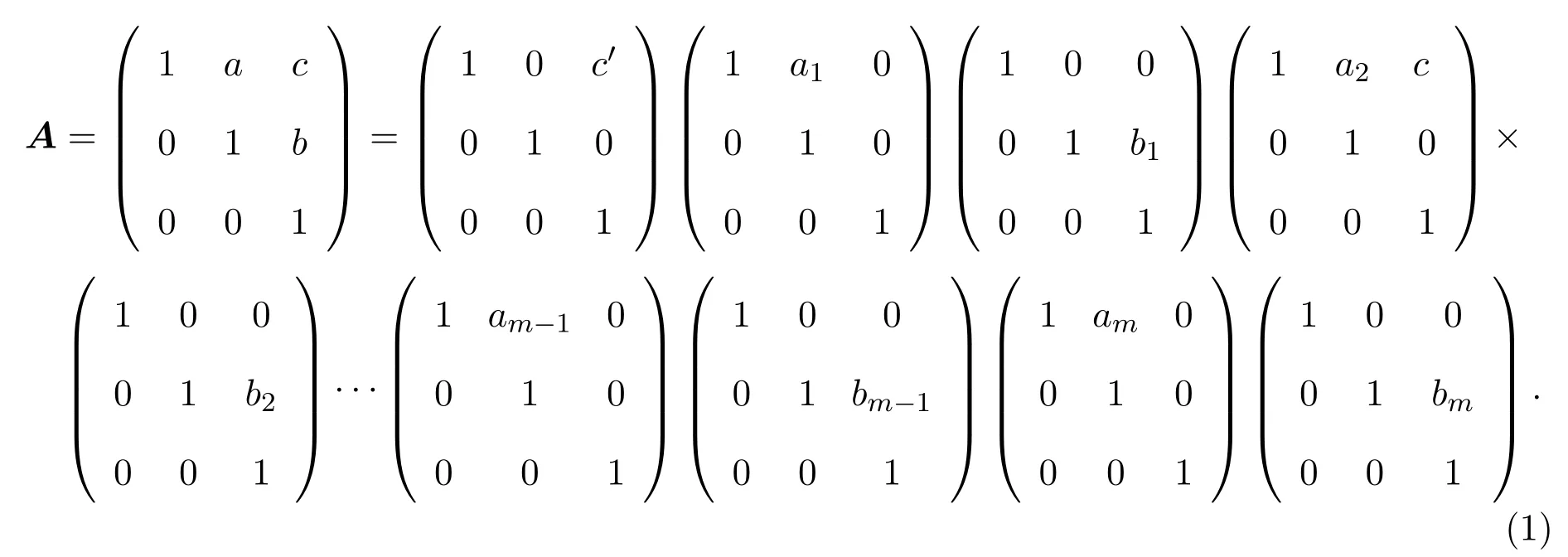
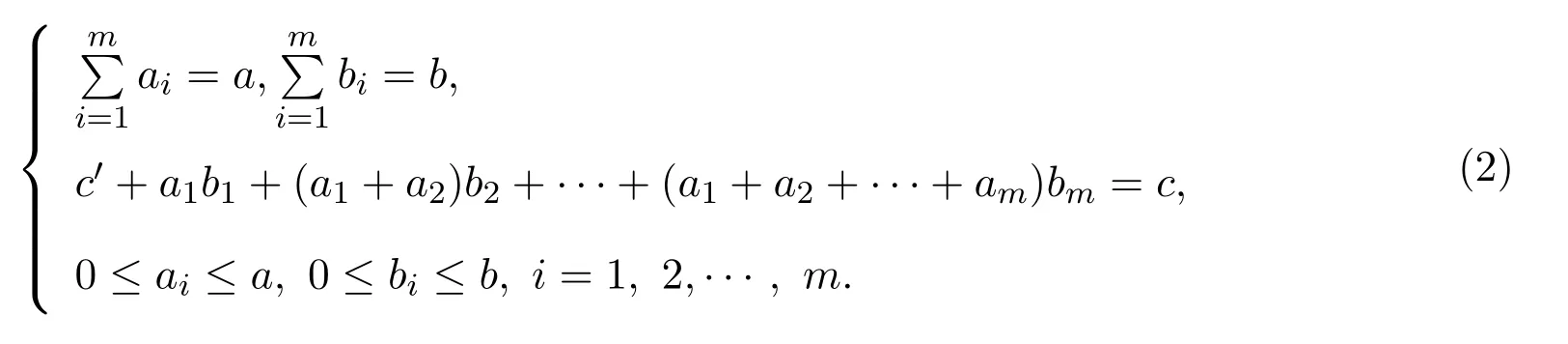
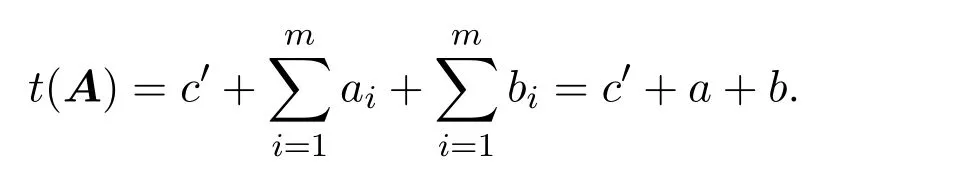
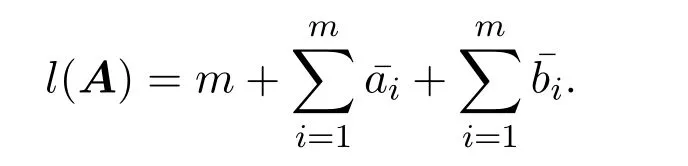
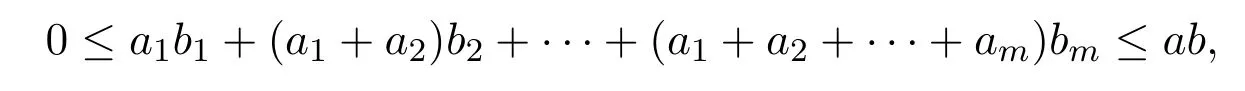
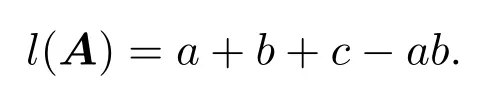
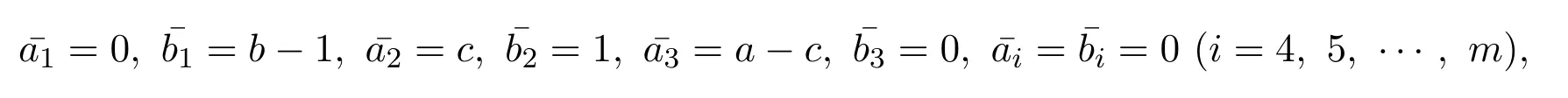
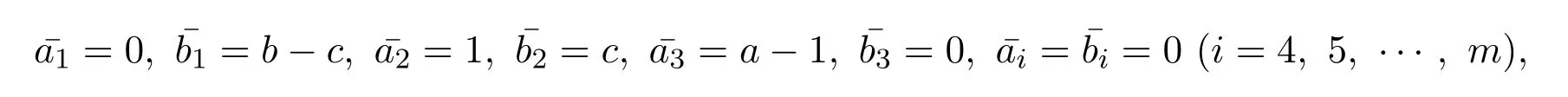
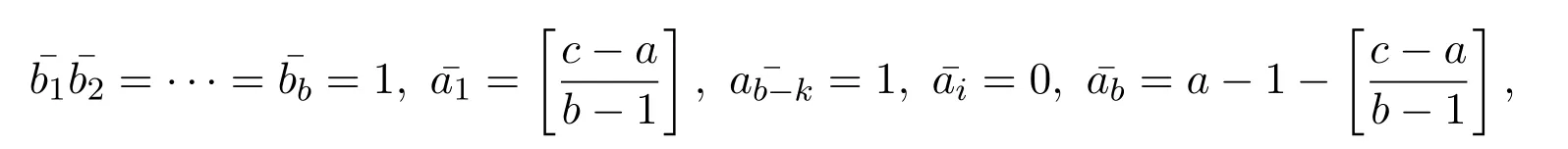
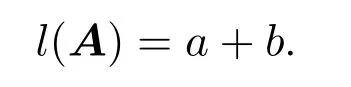
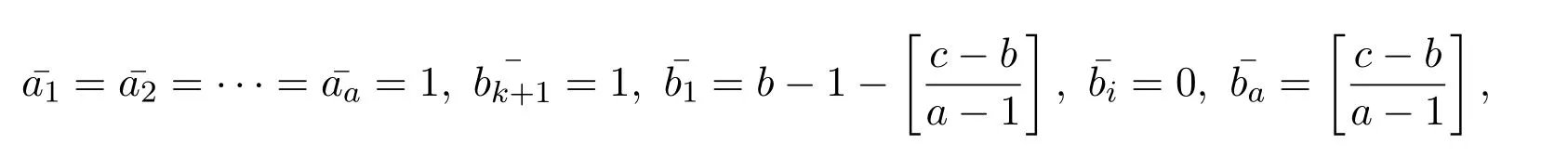
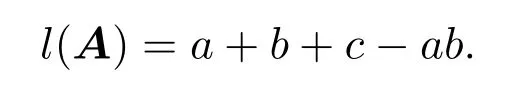
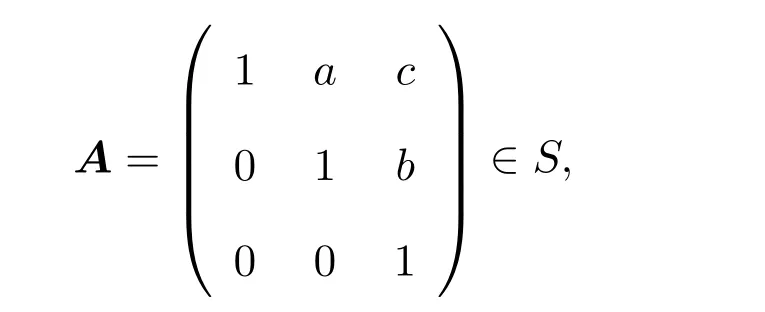
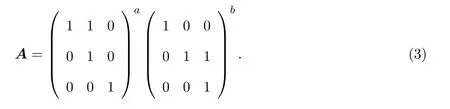

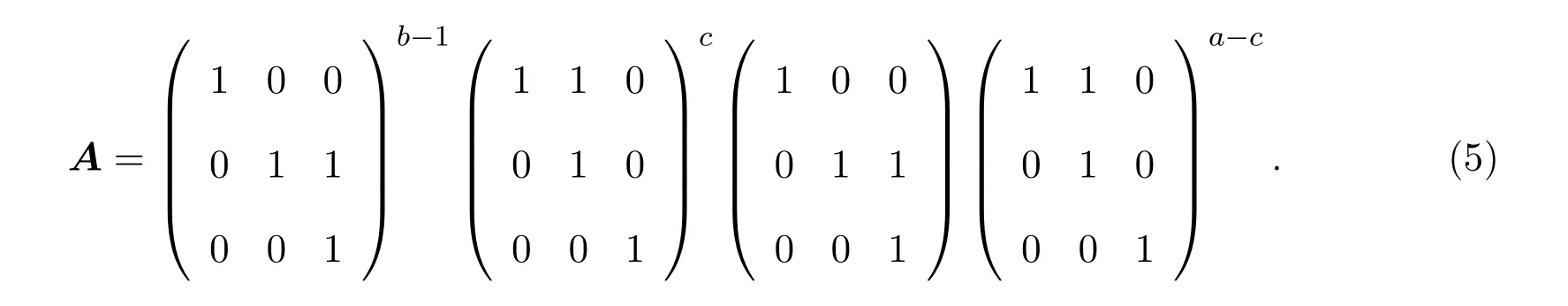
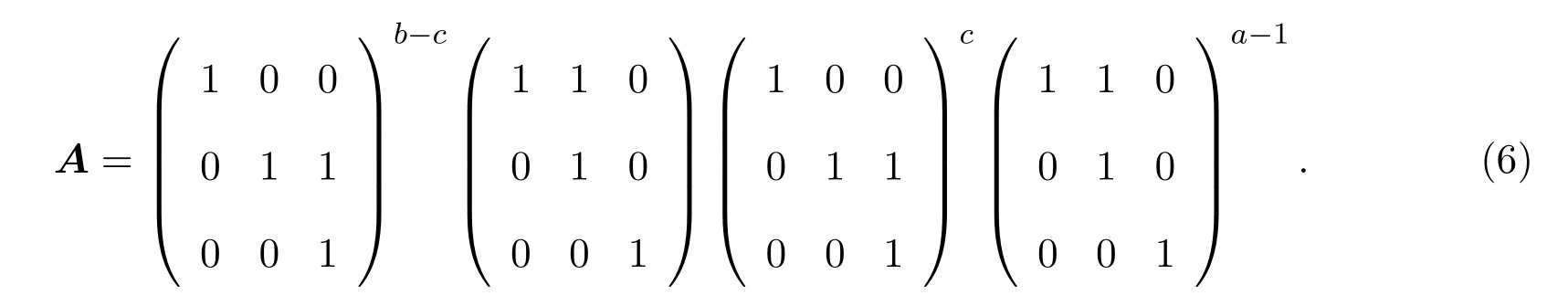

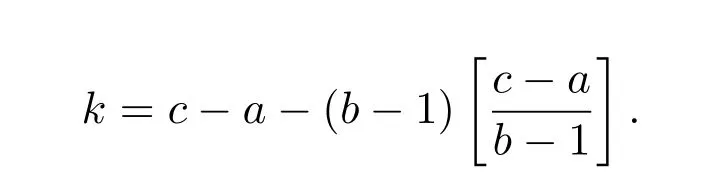

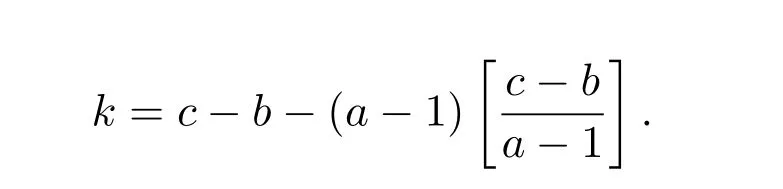
2.2 应用举例