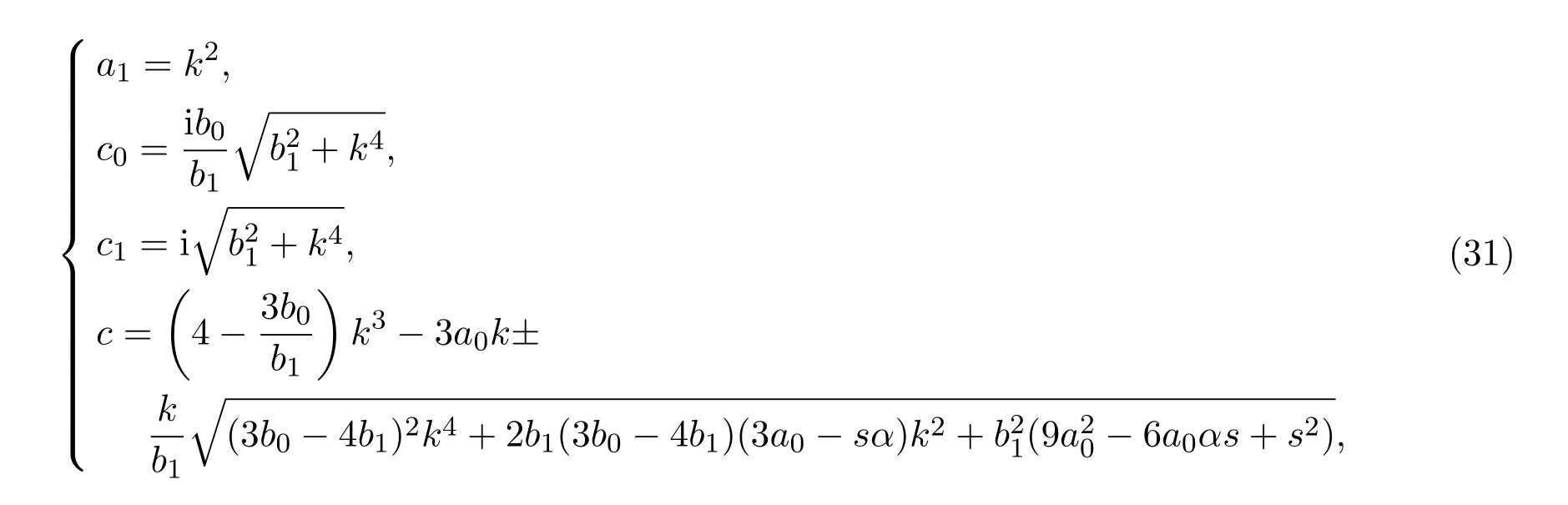双模Jordan KdV方程的多孤子解与精确解
2018-06-23赵露
赵露
(宁波大学数学系,浙江 宁波 315211)
1 引言
一般来说,大多数非线性方程都是关于时间t的一阶导数的方程,它们描述了单一方向的波.例如,KdV方程,Burgers方程等,这些模型均是沿x轴正向传播.Boussinesq方程是关于时间t的二阶导数的方程,它沿x轴正向和负向两个方向传播.然而,在1994年,文献[1]第一次提出了双模KdV(TKdV)方程,它是关于时间t的二阶导数的方程,描述了沿同一方向传播的两个不同的波的传播.这两个波具有相同的耗散关系,不同的像速,线性和非线性参数.双模KdV方程定义如下:
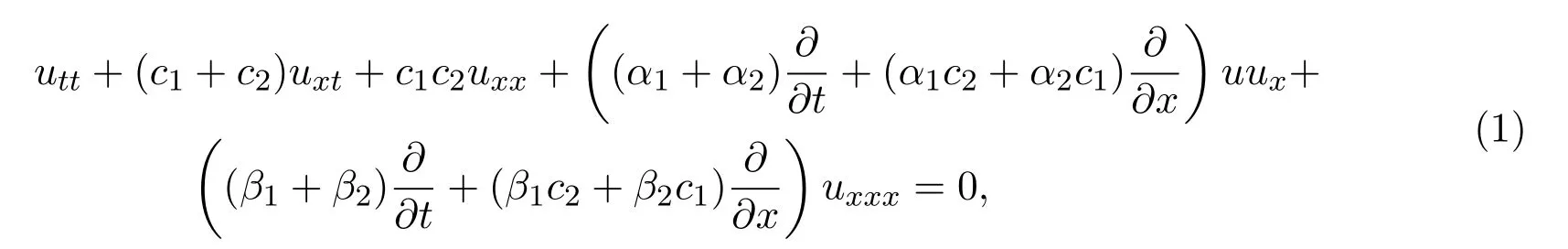
其中u(x,t)是场函数,ci(i=1,2)表示像速度,αi为非耗散系数,βi为耗散系数,且x,t,α,β满足
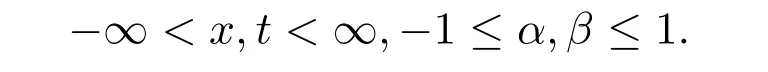
经过特殊的变换,方程(1)可以约化为:

其中
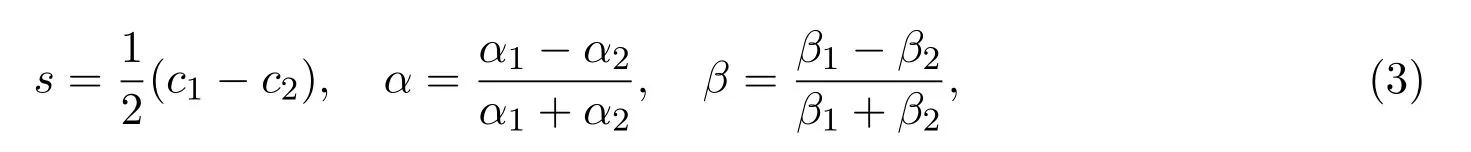
可以看出,当s=0时,TKdV方程(1)就约化为了标准形式的KdV方程.
文献[2-12]中给出了TKdV方程(2)的一些性质.其他的双模方程也已经被研究,例如双模mKdV方程[13],双模KP方程[14],双模Burgers方程[15]和双模耦合的KdV方程[16]等[17-20].本文将研究Jordan KdV(JKdV)方程组:
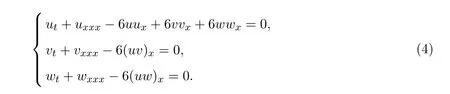
该方程组首次在文献[21]中提出.其中,当u=v=w时,JKdV方程组(4)可约化为标准的KdV方程.根据Korsunsky在文献[1]中提出的方法,构造新的双模Jordan KdV(TJKdV)方程组,即
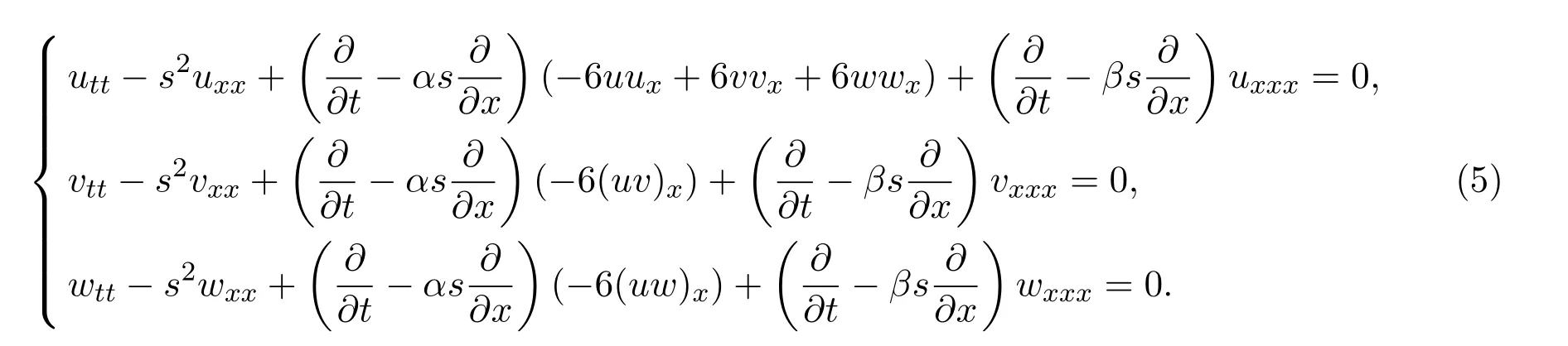
当s=0时,TJKdV方程组(5)可以约化为JKdV方程组(4).
本文结构安排如下:第二节,利用简化的双线性方法[22-25],找到了TJKdV方程组(5)的多孤子解存在的条件.第三节,利用tanh/coth方法和tan/cot方法找到TJKdV方程组的其他精确解.
2 多孤子解
在本节中,将利用简化的双线性方法研究双模Jordan KdV(TJKdV)方程组的多孤子解.把方程组
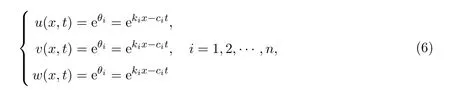
代入方程组(5)中并比较线性项与非线性项,得到耗散关系
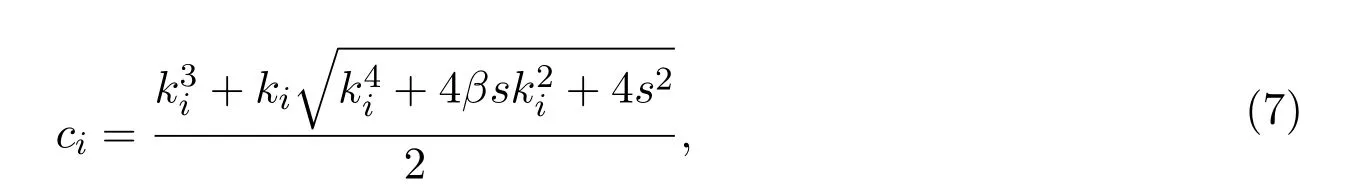
因此
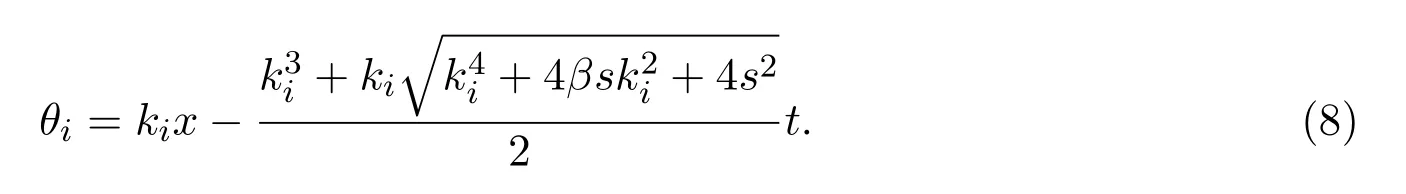
利用cole-hopf变换
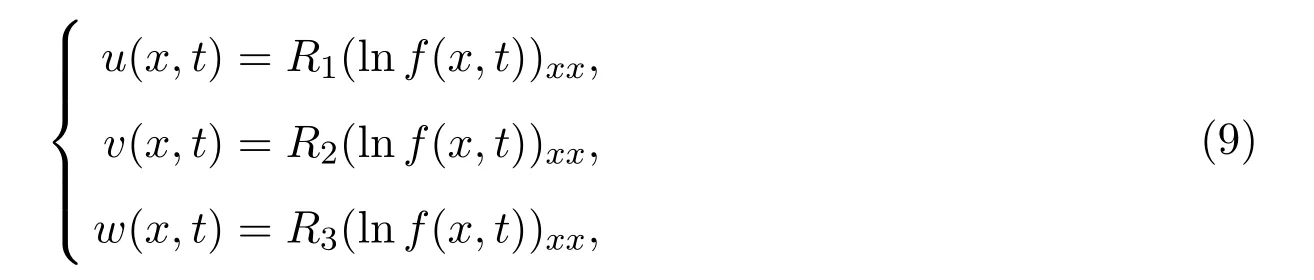
其中R1,R2,R3为待定常数.对于单孤子解我们令函数f(x,t)为:
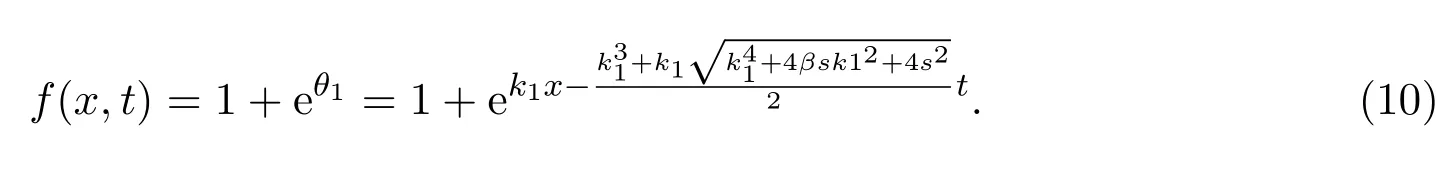
把方程(9),(10)代入TJKdV方程组(5)并求解R1,R2,得到当
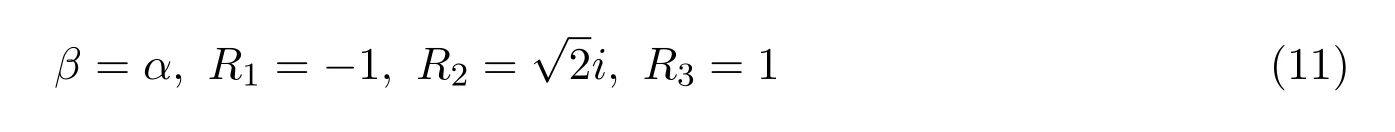
时,单孤子解存在.把(11)式与(10)式代入方程组(9),可得TJKdV方程组(5)的单孤子解如下:

对于二孤子解,令
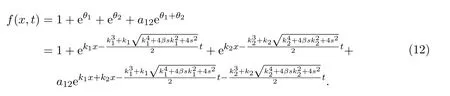
把方程(9),(12)代入TJKdV方程组(5)并求解a12,可得当
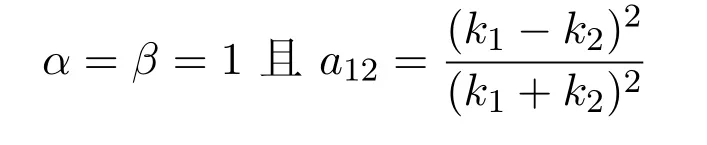
时,二孤子解存在.利用同样的方法可以得到a23,a13的具体表达式,即
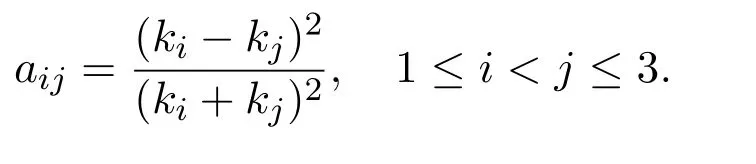
因此二孤子解为
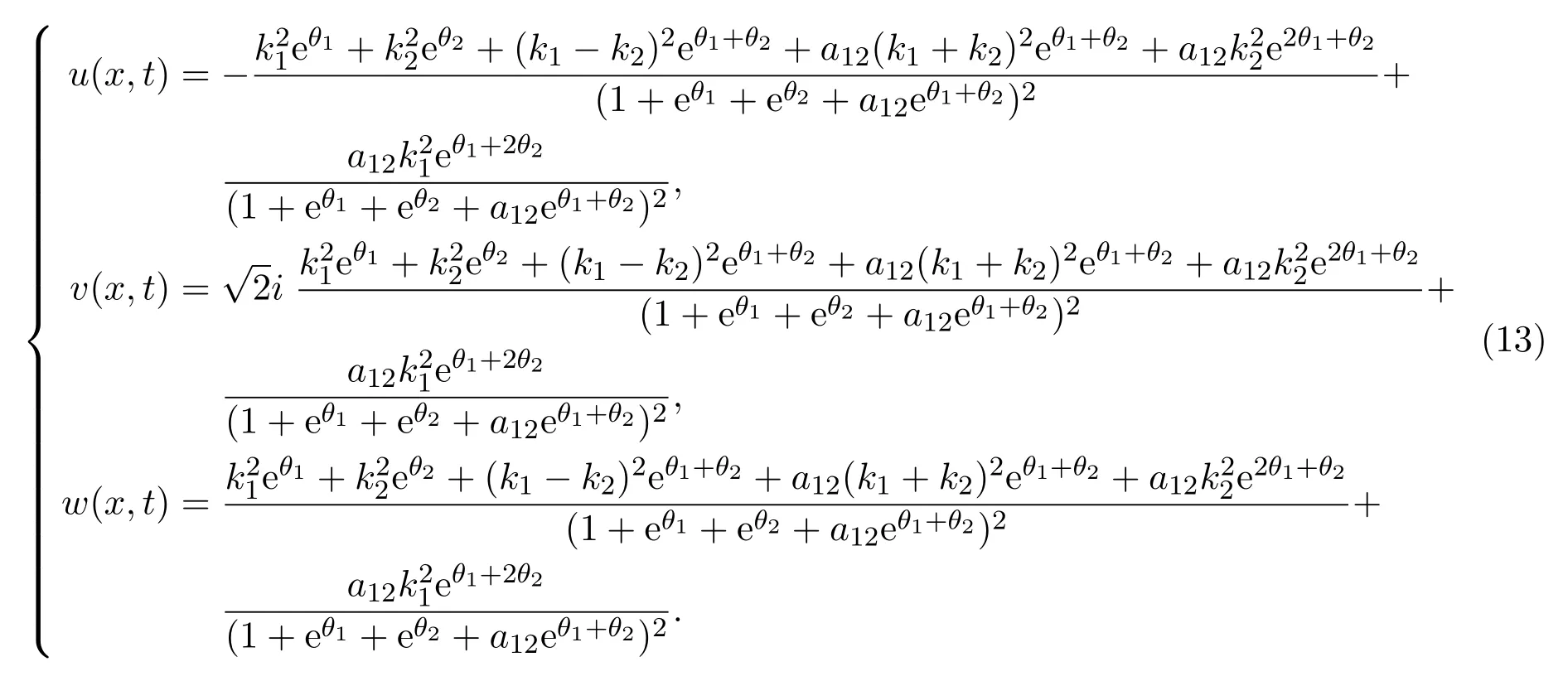
为了得到三孤子解,令
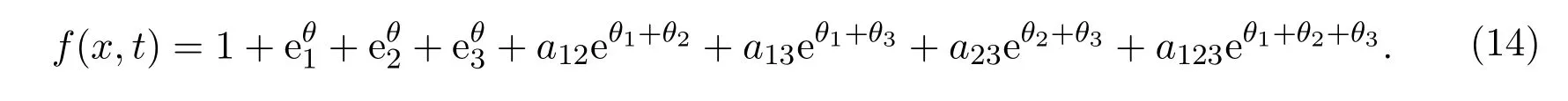
其中θi(i=1,2,3)由(8)式决定,aij(1≤i 把方程(9)和方程(14)代入TJKdV方程组(5)并求解a123,得到 经过第2节的讨论,我们知道孤子解存在只是针对特殊的α,β值,而对于一般的非耗散参数α与耗散参数β值,孤子解是否存在,我们并未讨论,并且这也是迄今为止未解决的问题.而在接下来的研究中,将会对一般的α和β的值来求TJKdV方程组的精确解. 在本节中,我们将会利用tanh/coth方法来求TJKdV方程组的精确解.设 把(15)代入方程组(5),在所得方程中平衡非线性项与耗散项可得 则 把方程组(16)代入TJKdV方程组(5)并比较所得方程中tanh(kx−ct)的各次幂的系数,得到 由 (17)式及 (16),得解 若设 与tanh(kx−ct)方法的步骤相似,可求得奇异解 把方程组(16)代入TJKdV方程组(5)并令β=α,在所得方程中比较tanh(kx−ct)的各次幂的系数,可以得到 这里的a0,b0,b1为非零常数,由(21)及(16)式,得解 其中c由(21)式决定. 若设 与tanh(kx−ct)方法的步骤相似,可求得奇异解 其中a0,b0,b1为非零常数,c由(21)式决定. 在本节中,利用tan/cot方法来求TJKdV方程组的精确解.设 把(25)式代入方程组(5),在所得方程中平衡非线性项与耗散项可得 则 下面分两种情况讨论. 把方程组(26)代入TJKdV方程组(5)并比较所得方程中tan(kx−ct)的各次幂的系数,得到 由 (27)及 (26)式,得解 其中a0,a1,c1为非零常数,c满足(28)式. 若设 与tan(kx−ct)方法的步骤相似,可求得奇异解 其中a0,a1,c1为非零常数,c满足(28)式. 把方程组(26)代入TJKdV方程组(5)并令β=α,在所得方程中比较tan(kx−ct)的各次幂的系数,可以得到 这里的a0,b1,b2为非零常数,因此可得解 其中a0,b0,b1为非零常数,c满足(31)式. 若设 与tan(kx−ct)方法的步骤相似,可求得奇异解 其中a0,b0,b1为非零常数,c满足(31)式. [1]Korsunsky S V.Soliton solutions for a second-order KdV equation[J].Physics Letters A,1994,185(2):174-176. [2]Lee C T,Liu J L,Lee C C,et al.The second-order KdV equation and its soliton-like solution[J].Modern Physics Letters B,2009,23(14):1771-1780. [3]Lee C T.Some notes on a two-mode Korteweg-de Vries equation[J].Physica Scripta,2010,81(6):1-13. [4]Lee C C,Lee C T,Liu J L,et al.Quasi-solitons of the two-mode Korteweg-de Vries equation[J].The European Physical Journal Applied Physics,2010,52(1):1-8. [5]Lee C T,Liu J L.A Hamiltonian model and soliton phenomenon for a two-mode KdV equation[J].Rocky Mountain J.Math.,2011,41(4):1273-1289. [6]Lee C T,Lee C C.On wave solutions of a weakly nonlinear and weakly dispersive two-mode wave system[J].Waves in Random and Complex Media,2013,23(1):56-76. [7]Lee C T,Lee C C,Liu M L.Double-soliton and conservation law structures for a higher-order type of Korteweg-de Vries equation[J].Physics Essays,2015,28(4):633-638. [8]Lee C T,Lee C C.On the study of a nonlinear higher order dispersive wave equation:its mathematical physical structure and anomaly soliton phenomena[J].Waves in Random and Complex Media,2015,25(2):197-222. [9]Lee C T,Lee C C.Symbolic computation on a second-order KdV equation[J].Journal of Symbolic Computation,2016,74:70-95. [10]Alquran M,Jarrah A.Jacobi elliptic function solutions for a two-mode KdV equation[J].Journal of King Saud University-Science,2017,24:35-41. [11]Xiao Z J,Tian B,Zhen H L,et al.Multi-soliton solutions and B¨acklund transformation for a two-mode KdV equation in a fluid[J].Waves in Random and Complex Media,2017,27(1):1-14. [12]Wazwaz A M.Multiple soliton solutions and other exact solutions for a two-mode KdV equation[J].Mathematical Methods in the Applied Sciences,2017,40(6):2277-2283. [13]Wazwaz A M.A two-mode modi fied KdV equation with multiple soliton solutions[J].Applied Mathematics Letters,2017,70:1-6. [14]Wazwaz A M.A study on a two-wave mode Kadomtsev-Petviashvili equation:conditions for multiple soliton solutions to exist[J].Mathematical Methods in the Applied Sciences,2017,21:4128-4133. [15]Wazwaz A M.A two-mode Burgers equation of weak shock waves in a fluid:multiple kink solutions and other exact solutions[J].International Journal of Applied and Computational Mathematics,2016,21:1-9. [16]Jaradat H M,Syam M,Alquran M.A two-mode coupled Korteweg-de Vries:multiple-soliton solutions and other exact solutions[J].Nonlinear Dynamics,2017,25:1-7. [17]Wazwaz A M.Two-mode fifth-order KdV equations:necessary conditions for multiple-soliton solutions to exist[J].Nonlinear Dynamics,2017,87(3):1685-1691. [18]Wazwaz A M.Two-mode Sharma-Tasso-Olver equation and two-mode fourth-order Burgers equation:Multiple kink solutions[J].Alexandria Engineering Journal,2017,71:25-31. [19]Jaradat H M.Two-mode coupled Burgers equation:multiple-kink solutions and other exact solutions[J].Alexandria Engineering Journal,2017,34:1-5. [20]Syam M,Jaradat H M,Alquran M.A study on the two-mode coupled modi fied Korteweg-de Vries using the simpli fied bilinear and the trigonometric-function methods[J].Nonlinear Dynamics,2017,23:1-9. [21]Svinolupov S I.Jordan algebras and integrable systems[J].Functional Analysis and Its Applications,1993,27(4):257-265. [22]Hirota R.Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons[J].Physical Review Letters,1971,27(18):1192-1194. [23]Matsuno Y.Bilinear Transformation Method[M].New York:Elsevier,1984. [24]Wazwaz A M.A reliable study for extensions of the Bratu problem with boundary conditions[J].Mathematical Methods in the Applied Sciences,2012,35(7):845-856. [25]Wazwaz A M.Multiple kink solutions for two coupled integrable(2+1)-dimensional systems[J].Applied Mathematics Letters,2016,58:1-6.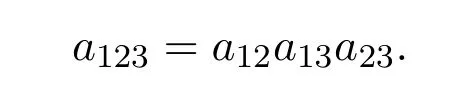
3 其它的精确解
3.1 tanh/coth方法
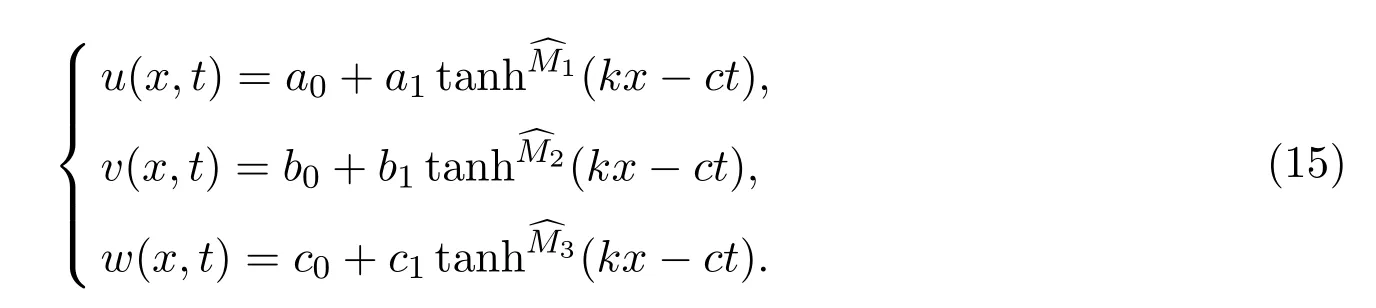
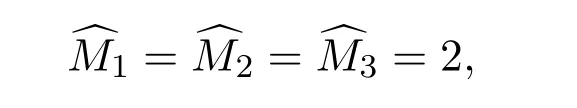
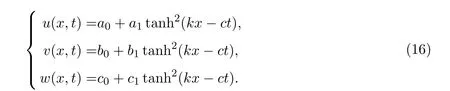
3.1.1 βα

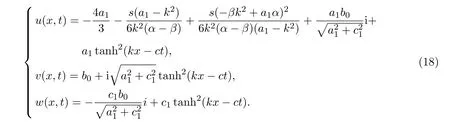
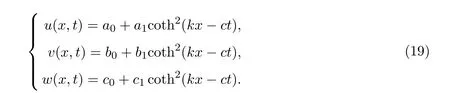
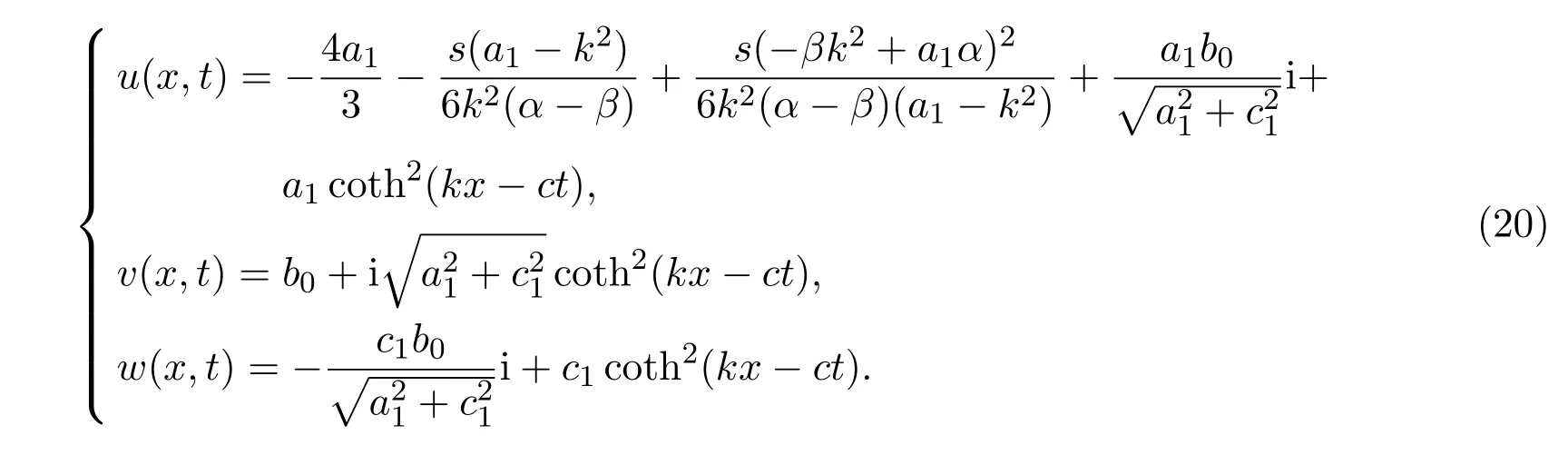
3.1.2 β=α

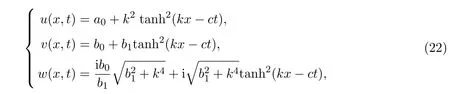
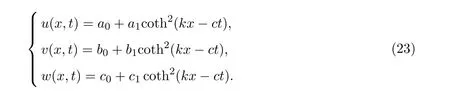
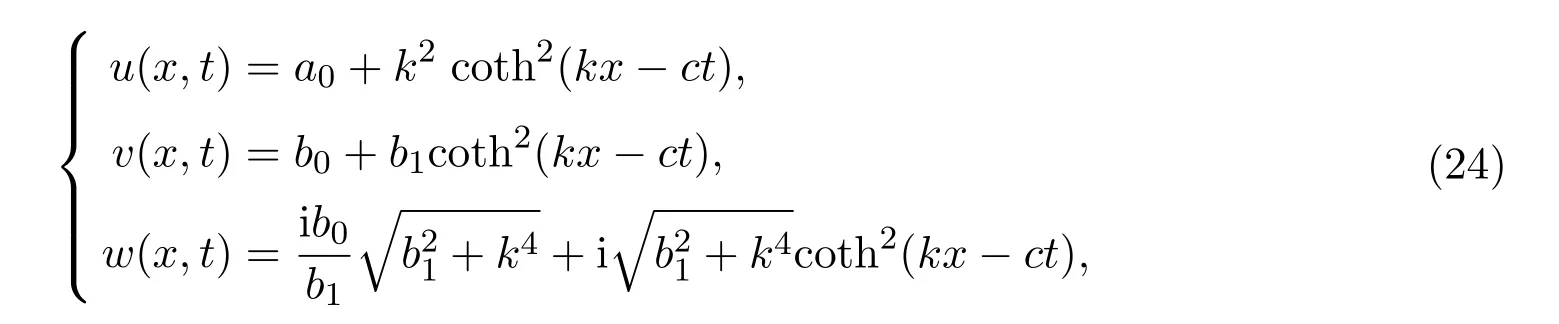
3.2 tan/cot方法
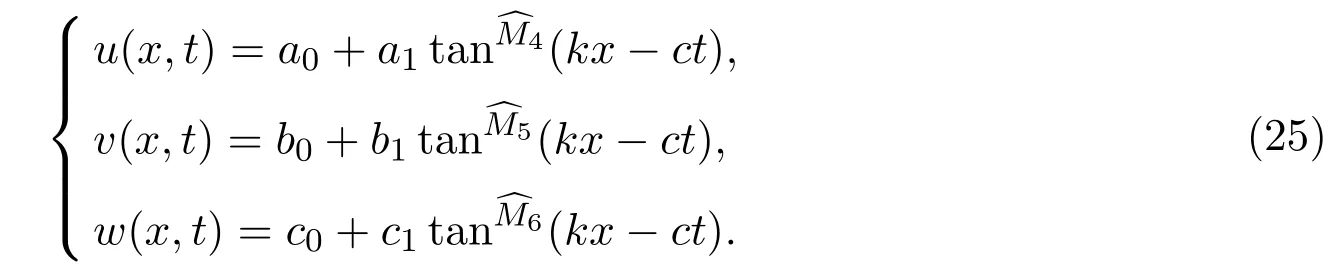
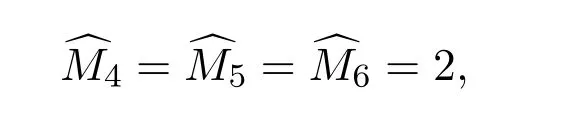
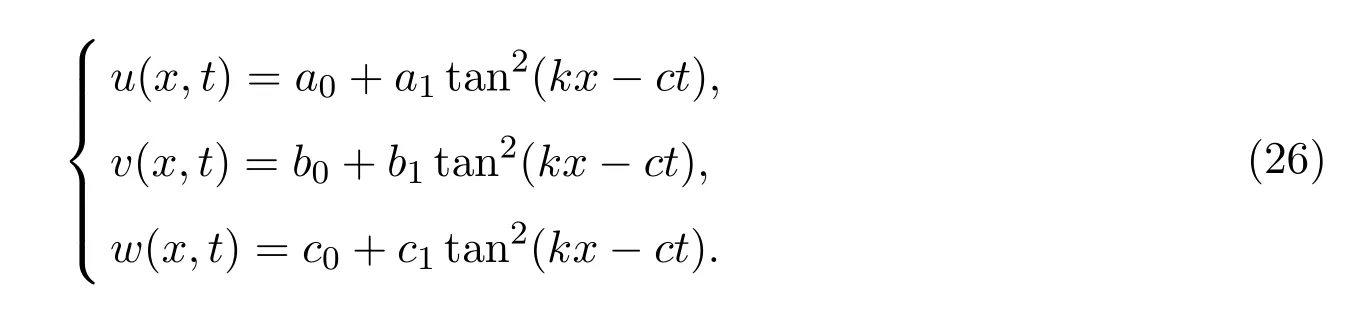
3.2.1 βα

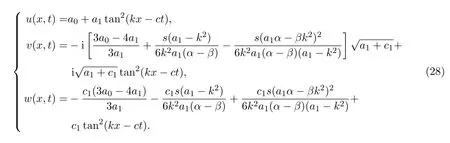
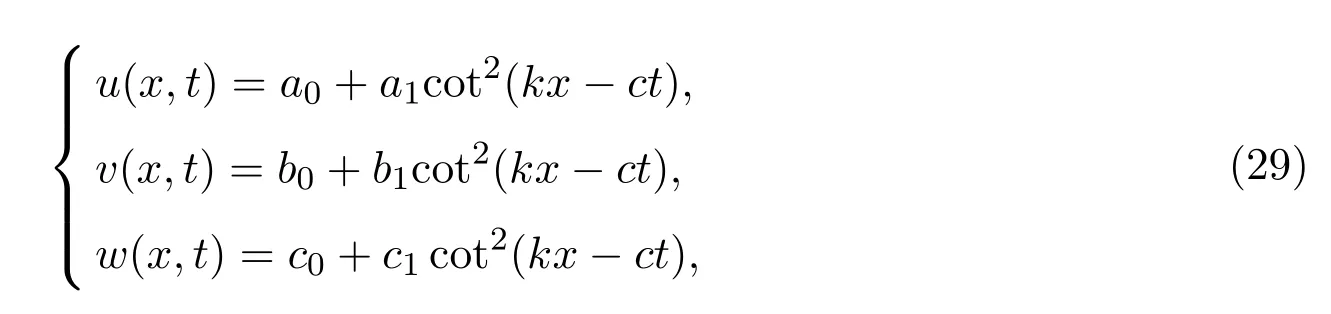
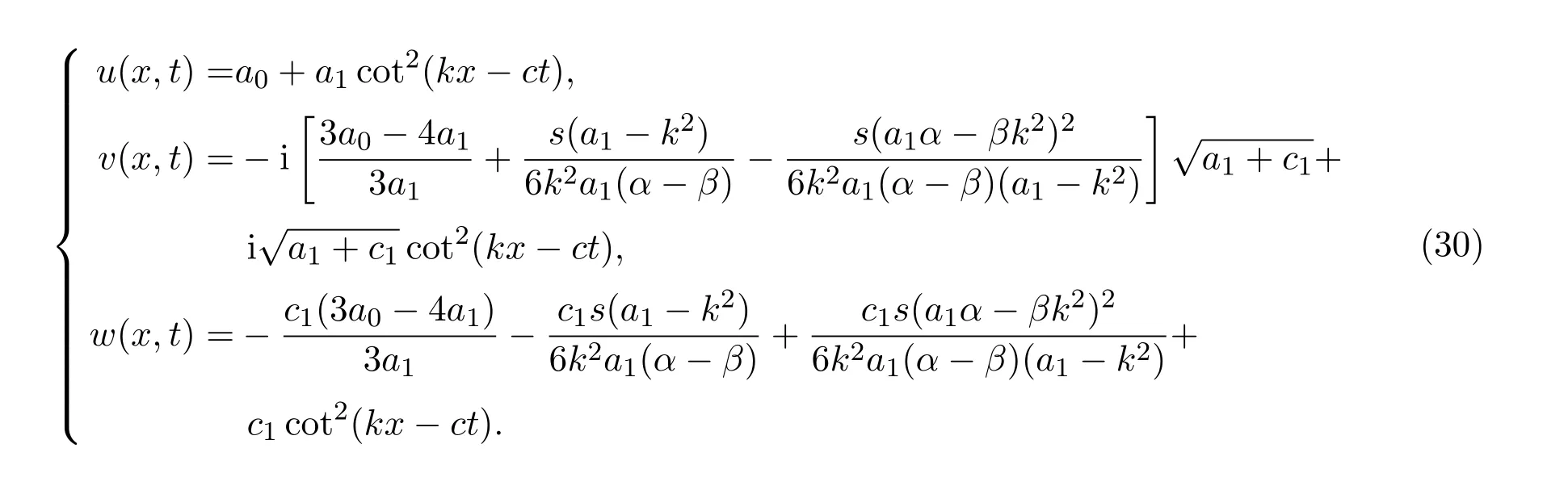
3.2.2 β=α