部分线性模型下Adaptive Dantzig Selector方法的渐近正态性
2018-06-23李丹丹刘琳
李丹丹,刘琳
(广西大学数学与信息科学学院,广西 南宁 530004)
1 引言
变量选择是进行数据分析以及统计建模过程中比较重要的部分.近年来,由于大量超高维数据的涌现,变量选择引起了学者的高度重视.随着研究的不断深入,越来越多的变量选择方法与相对应的算法被提出.其中最典型的代表是Lasso(Least Absolute Shrinkage and Selection Operator)方法.Lasso[1]方法的提出迅速引起了很多学者的关注,在研究的过程中Lasso方法的局限性也突显出来,文献[2]指出Lasso方法给出的估计不具有相合性以及大样本性质.为了解决这一问题,文献[3]提出DS(Dantzig Selector)方法,并研究了DS估计损失的非渐进界,但没有得出其渐进性质.之后文献[4]和文献[5]分别提出了处理超高维数据的ADS(Adaptive Dantzig Selector)方法和DASSO算法.在目前的文献中对ADS方法的研究仍较少,现考虑当维数随样本数以指数速度增长时,在部分线性模型下ADS方法的渐近正态性质.
2 ADS方法及其性质
2.1 部分线性模型下 ADS估计的定义
设X=(X1,X2,···,Xp)T是p维协变量,Y是响应变量,β=(β1,β2,···,βp)T为p维非零的参数向量,g(t)为未知的非参数函数,且g(·)光滑,ε是随机误差,E(ε/X,t)=0,则部分线性模型[6]形式如下:

对(1)式两边分别求关于t的条件期望,得到
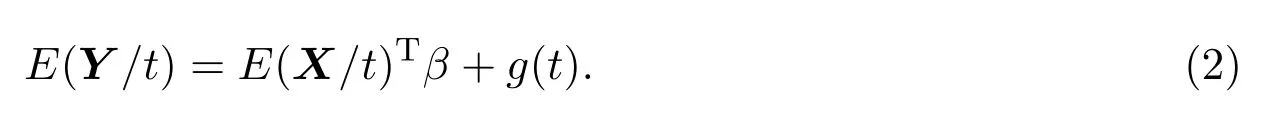
联立(1)(2)两式可得
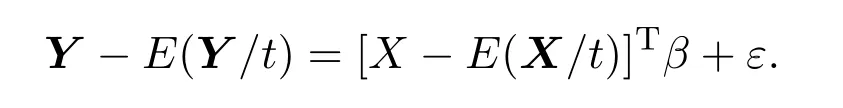
下面利用核估计方法,令mX(t)=E(X/t),mY(t)=E(Y/t),其中mX(t),mY(t)的估计
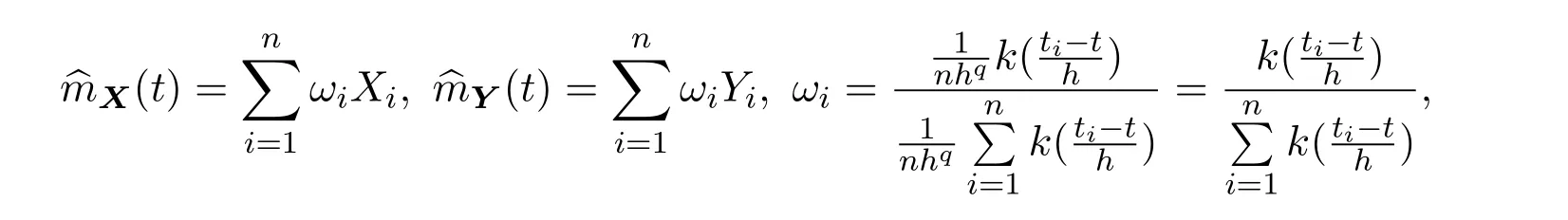
K(·)为核函数,h为窗宽.下面定义部分线性模型的DS[7]估计为:
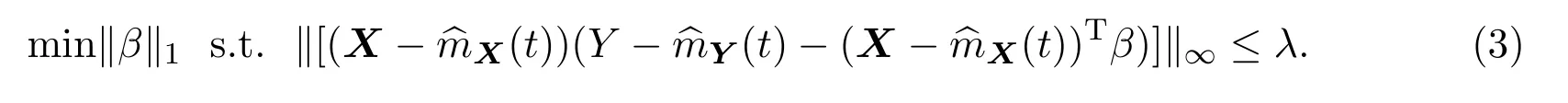
其中,λ为调整参数.令
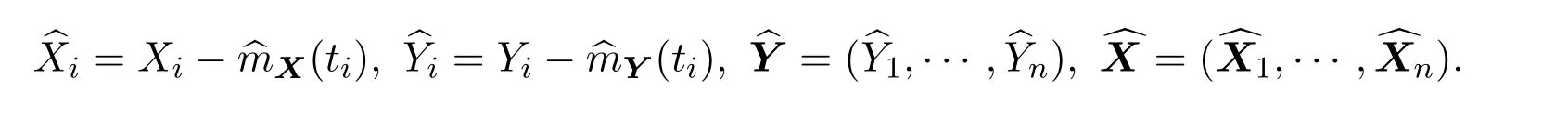
定义 2.1部分线性模型下的ADS估计,
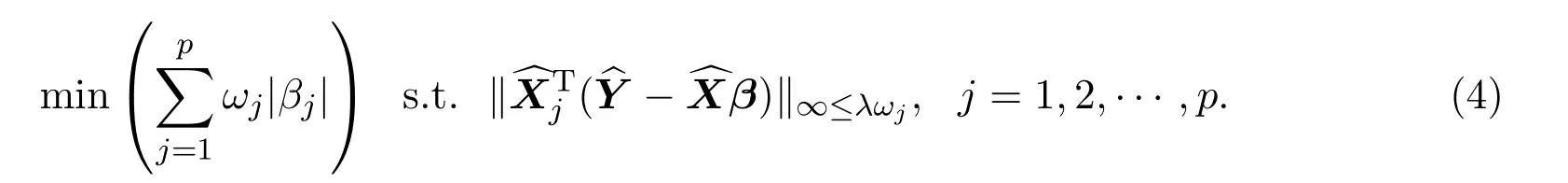
则所求解为ADS估计值,记为
此时非参数部分g(t)的估计为选取权重函数令W=diag(ω1,ω2,···,ωp),其中是的相合估计,f(·)是正的减函数,且f(0)=∞.
2.2 ADS估计的渐近正态性
设真实参数值稀疏,其中
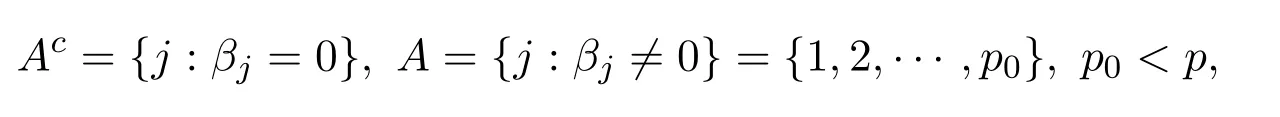
则
首先给出半参数模型中的正则条件:
1 设核函数K(·)关于原点对称,支撑区间为[−1,1],存在常数M1和M2,有 0≤M1≤M2,使得
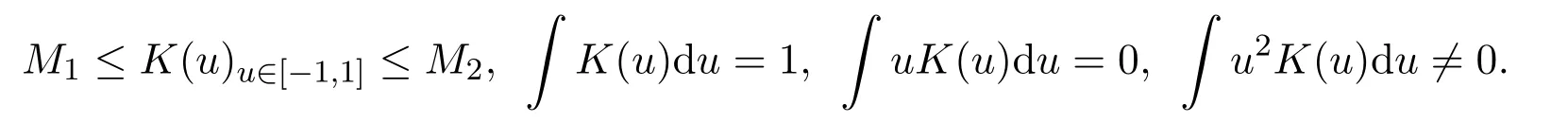
2
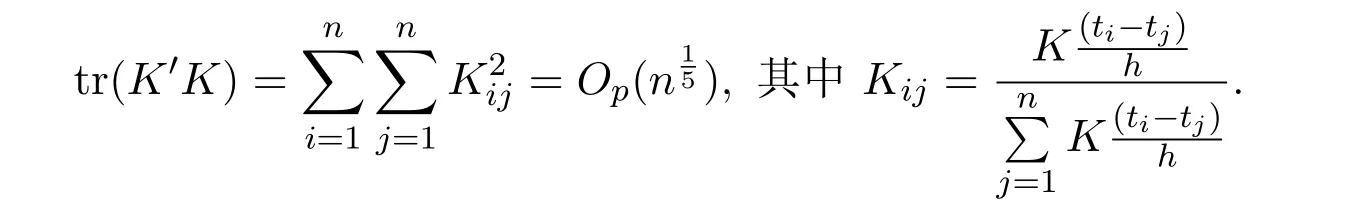
3t的密度函数不为0,与mX(t),mY(t)都是二阶导数连续有界,其中mX(t),mY(t)估计选择的窗宽h的阶数为
接下来给出四个条件假设:
(a)假设误差项ε1,···,εn独立同分布,并对某常数1≤d≤2,L>0和K,对任意的x≥0和i=1,2,···,εi,p(|εi|>x)≤Kexp(−Lxd)的尾概率均满足,使维数p随着样本数n以指数速度exp(nα)增长,其中0<α<1.
(b)假设初始估计满足其中ηj是依赖于β的未知常数,满足如下不等式
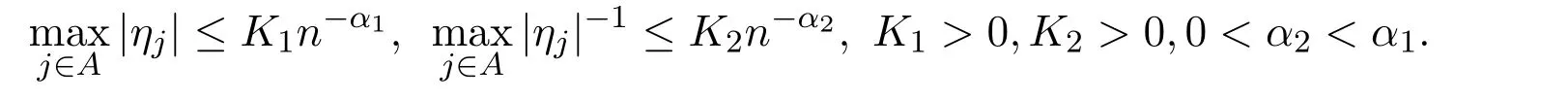
(c)设q为通过变量选择得到的变量个数,记为|A|.由q=O(nc1),0 成立,其中k为常数,Σ是p×p维矩阵,ΣAA是Σ中|A|×|A|维子矩阵组成,0 (d)设 其中XAi表示矩阵XA的第i列. 说明:假设条件(a)保证了维数p随着样本数n以指数速度exp(nα)增长,对于(b)中系数的初始估计的取法,Huang[8]提出在适当条件下可以用边际回归估计量来作为ALasso(Adaptive Least Absolute Shrinkage and Selection Operator)方法的初始估计,类似的方法,可在(b)中取 先用边际回归估计量得到回归系数的初始估计再用来作为ADS方法的权重,结合(c)(d)假设可得在部分线性模型下ADS方法的渐近正态性,下面给出具体的证明. 定理 2.1若及假设条件(a)至(d)成立时,p随着样本数n以指数速度exp(nα)增长,其中0<α<1.则部分线性模型ADS参数估计量满足 证明根据设(4)式的解为其中 I为单位阵,K=(Kij)n×n.由假设条件 (a)至(d),则有 根据条件(d),令则 所以由slutsky定理,得 通过上述得到维数p关于样本数n以指数速度增加时,在部分线性模型下ADS方法具有渐近正态性,即在处理超高维稀疏数据时,可以达到有效降维和确保模型准确率的目的.下面通过数值模拟来验证该方法的可行性与优越性. 假设数据取自模型为 其中g(t)=sin(2πt),t服从 [0,1]上的均匀分布ε∼N(0,1),真实参数β有六个非零分量β=(1,3,1,3,1/2,1/2,0,···,0)取n=50,非参数估计核函数为Epanechnikov核,K(µ)=0.75(1−µ2)+,调整参数采用BIC惩罚参数选取法,取维数p=100,500,在R软件编辑程序,并重复运行1000次,取其非零系数估计结果的平均数进行汇总为如表1所示. 表1 两种方法的系数估计平均值 通过数值模拟结果可以看出,当p≫n时,ADS方法得到的估计值与Lasso方法相比更接近真值,故验证了该方法的优良性. 下面通过实例进一步验证在大众点评网数据中的可行性. 本文将 ADS方法用于大众点评网数据 (http://www.dianping.com/beijing),数据集共由1000多家美食类商家数据组成,主要选取了消费者关心的信息指标以及直接影响消费者决策判断的数据进行收集.将销售量作为响应变量记为:Y,将店铺星级、店铺动态评分(即口味、环境、服务)、人均消费价格、好评,一般,差评的数量,以及32种菜系等40个指标作为协变量记为:X1,X2,X3,···,X39,X40.通过分析,可得Y与X符合部分线性模型条件,找出与Y存在较显著的非线性关系的协变量,将其作为非参数模型中g(·)的协变量.在R软件中,可利用LARS算法与DASSO算法,同时采用五折交叉验证法选取惩罚参数λ,结果如表2所示,其中两种方法系数估计值全为0的已略去. 表2 模型非零系数的估计值 将预测模型代入检测集中得出模型的验证结果如表3所示: 表3 两种方法验证结果比较 在表3中,CSR(Correct Selection Rate)表示模型选择的正确率,即在检测集中能正确预测出的个数/检测集的总个数,MSE(Mean Square Error)表示均方误差值表示检测集中的数据,表示预测结果取整后的值,N(Number)表示模型中被选入变量的个数.从表3的验证结果中可以看出: 1.对于CRS值,Lasso方法所对应的CRS值为80.95%小于ADS方法的83.72%; 2.对于MSE值,模型中Lasso方法对应的MSE值是大于ADS方法的MSE值; 3.对于N值,在模型中Lasso方法比ADS方法在变量选择时多选入了2个变量,且ADS方法能从40个变量中准确的选出7个对销售量有显著影响的特征变量. 结合上述结论,得出ADS方法在实际应用中的可行性以及高精准性. 本文首先给出部分线性模型下ADS方法的定义,并证明了在超高维情况下,p维数随样本数n以指数速度增长时,在部分线性模型下ADS方法的渐近正态性质.然后通过数值模拟并结合大众点评网美食店铺的数据,通过比较ADS方法与Lasso方法的计算结果,进一步验证了在部分线性模型下ADS方法在处理超高维稀疏性数据时的大样本性质,以及在实际应用中的可行性以及高精准性. [1]Tibshirani R.Regression shrinkage and selection via the Lasso[J].Journal of the Royal Statistical Society,2011,73(3):273-282. [2]Zhao P,Yu B.Stagewise Lasso[J].Journal of Machine Learning Research,2014,8(12):2701-2726. [3]Candes E,Tao T.The Dantzig Selector:statistical estimation whenpis much larger thann[J].The Annals of Statistics,2007,35(6):2392-2404. [4]Dicker L,Lin X.Parallelism,uniqueness,and large-sample asymptotics for the Dantzig selector[J].Canadian Journal of Statistics,2013,41(1):23-35. [5]James G M,Radchenko P.A generalized Dantzig selector with shrinkage tuning[J].Biometrika,2009,96(2):323-337. [6]董凯.高维数据部分线性模型的变量选择[D].北京:北京工业大学图书馆,2012. [7]Li F.Variable selection and parameter estimation for partially linear models via Dantzig selector[J].Metrika,2013,76(2):225-238. [8]Huang J,Ma S.Adaptive lasso for sparse high-dimensional regression models[J].Statistica Sinica,2006,18(4):1603-1618. [9]Dicker L H.Regularized Regression Methods for Variable Selection and Estimation[D].Boston:Harvard University,2010.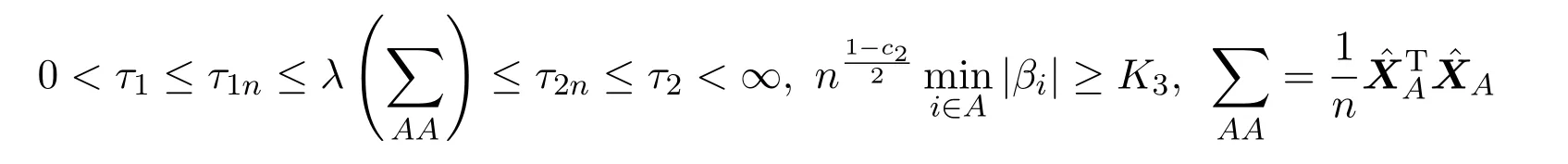
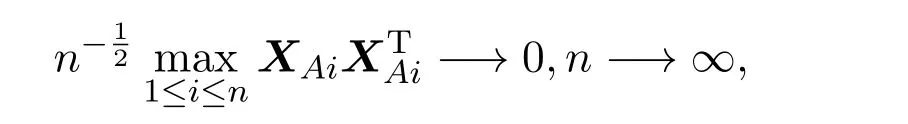
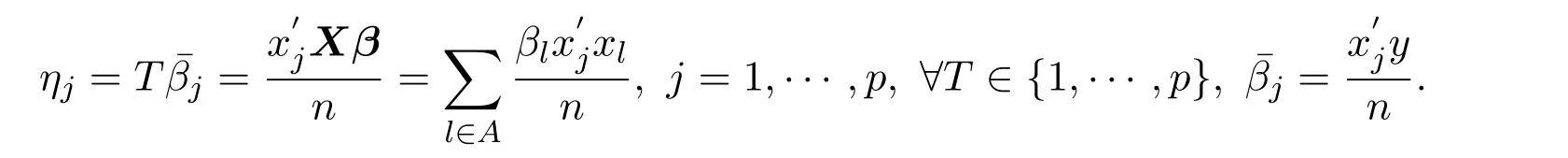
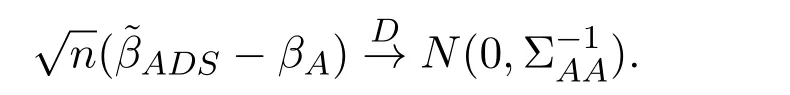
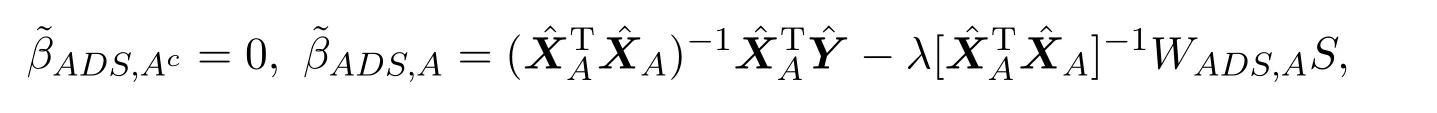

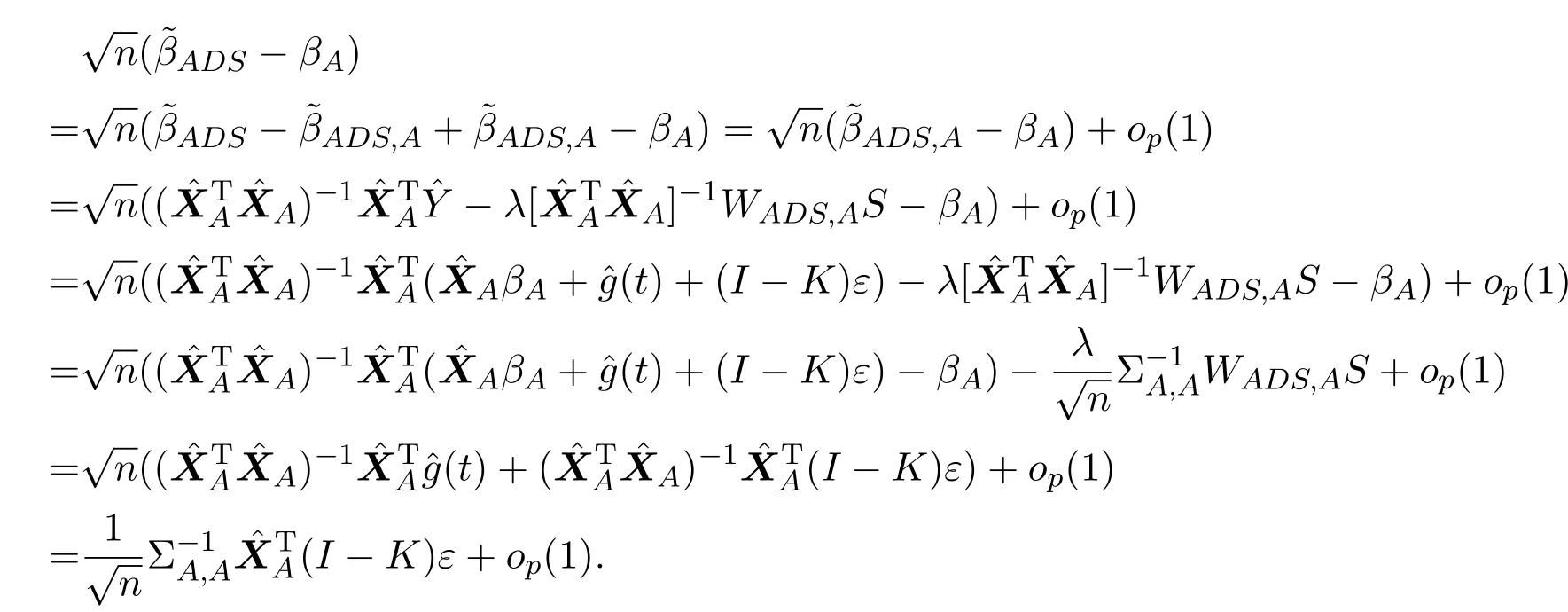
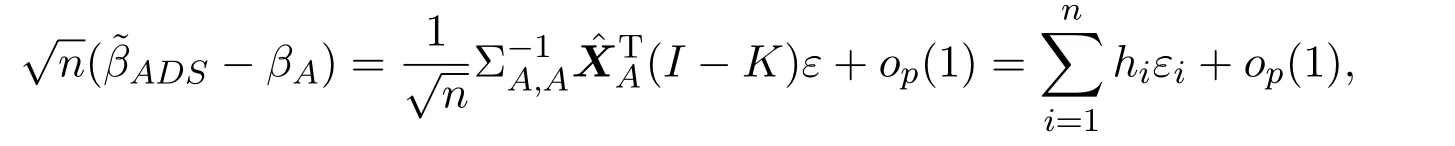
3 数值模拟
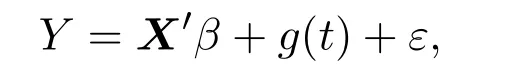

4 实例分析


5 结论
